Large-scale repositories
These are big collections of texts, big enough to act as small library-like collections in their own right. The threshold for inclusion here may rise over time. Listed alphabetically.
- Google Books (page images of 10,000,000+ fully readable volumes, plus many more copyrighted books available via excerpts and snippets)
- Advanced Book Search (may be easier to find specific free titles via this page)
- HathiTrust Digital Library (3,000,000+ freely readable titles, and additional search-only titles, from Google and elsewhere)
- Internet Archive Ebooks and Texts (20,000,000+ freely readable volumes; page images and some transcriptions)
- Project Gutenberg (over 50,000 items, mostly book transcriptions)
Significant indexes and search aids
The sites below primarily provide search engines, indexes or useful link lists for finding online books.
- ATHENA (multilingual text index in Switzerland)
- Digital Book Index (free and for-pay books online; registration-based)
- The Online Books Page (the site that includes this directory)
- Voice of the Shuttle and its English Literature section
Significant smaller-scale archives
Everything else we see worth listing that doesn’t fit in more specialized categories.
- Oxford Text Archive (in the UK)
- The Bibliomania Library (from Data Text)
- Electronic Open Stacks (preservation digitization at Chicago)
- National Library of Canada Electronic Collection (archives texts from or about Canada)
- IntraText Digital Library (5000+ texts, multilingual, main focus on religion, Latin, Italian, and science)
- Michigan Digital Public Text Collections (100+ collections open to the public)
- Project Gutenberg Canada (Literature in the public domain in Canada)
- Faded Page (4000+ books in the public domain in Canada)
- Roy Glashan’s Library (Literature in the public domain in Australia)
Non-English Languages
- Afghan languages (including Pashto and Dari): Afghanistan Digital Library
- Alaskan languages (including Aleut, Alutiiq, Tlingit, and Yup’ik): Alaskan Orthodox Texts
- Arabic: Arabic Collections Online (10,000+ public domain volumes; at NYU)
- Armenian: Armenian House Library (Armenian section)
- Australian indigenous languages: CALL Collection (books and other literature, with many items digitized)
- Catalan / Valencian:
- Biblioteca Virtual Joan Lluís Vives (mostly Catalan materials)
- Selecció de Poesia Catalana (Catalan poetry)
- Chamorro: Chamorro Bible website (also has other Chamorro literature and language resources)
- Chinese:
- Chinese Text Project (annotated Chinese classics)
- Classical Languages:
- An Analytical Bibliography of On-Line Neo-Latin Titles (index of over 60,000 items, edited by Dana Sutton)
- Ancient Greek and Latin Texts (selected from Google Books)
- Bibliotheca Augustana (Latin texts arranged by century)
- Electronic Resources for Medieval Philosophy Studies: Digitized Books (at Boston College)
- The Latin Library (edited by William L. Carey)
- Project Libellus (at the University of Washington)
- Perseus Digital Library (classical Greek, Latin, and other texts at Tufts)
- Textkit (Greek and Latin learning tools)
- Vatican Library Digital Collections (mostly in Latin)
- Czech: National Library of the Czech Republic Digital Libraries
- Danish: Arkiv for Dansk Litteratur (in Denmark)
- Dutch:
- Ars Floreat (philosophy and religion texts in Dutch)
- Delpher (100 million pages of historic Dutch-language texts)
- Digitale Bibliotheek voor de Nederlandse Letteren
- Ethiopian languages: Virtual Hill Museum Reading Room (includes Ethiopian and other languages)
- Farsi (Persian):
- Ketab Farsi (Farsi books online)
- Persianbooks (index at blogspot.com)
- French:
- ATHENA e-texts
- ARTFL Public Databases (free portion of this French literature collection)
- Association des bibliophiles Universels (public domain French texts; in France)
- Ebooks Libres et Gratuits (2000+ public domain French language books)
- Les Classiques des Sciences Sociales (French-language social science classics; at U. du Québec)
- Gallica from the Bibliotheque Nationale de France (5 million+ documents in French and other languages)
- Marandet Collection of French Plays (several digitized collections from before 1789 through 1835; at Warwick)
- Gaelic:
- CELT Project (Irish electronic texts)
- Corpas Stairiúil na Gaeilge / Historical Irish Corpus, 1600-1926 (at Royal Irish Academy)
- German:
- Austrian Literature Online (Austrian works, mostly in German)
- Göttinger Digitalisierungszentrum (German and some English etexts)
- MATEO (Mannheim texts online)
- Sophie (work by German-speaking women; at BYU)
- Projekt Gutenberg-DE (German texts; no direct relation to the US-based Project Gutenberg)
- Religio (Texts in German on religion)
- WikiSource: Zeitschriften (list of links to digitized pre-1930 German periodicals)
- Zeno.org (free German literature)
- Hawaiian:
- Hawaiian Language Newspapers (at hawaii.edu)
- Ulukau: The Hawaiian Electronic Library
- Hebrew:
- Daat (includes medieval Jewish philosophy full texts)
- HebrewBooks.org (over 50,000 out of print Seforim and other classical Hebrew books)
- International Collection of Digitized Hebrew Manuscripts (at National Library of Israel)
- Mechon Mamre (classical Jewish texts and others)
- Project Ben-Yehuda (in Israel)
- Sefaria Library (religious texts in Hebrew and other languages)
- Tshuvos.com (Tshovos seforim)
- Yizkor Books (Holocaust memorial books; at NYPL)
- Hungarian: Magyar Elektronikus Könyvtár (Hungarian electronic library)
- Icelandic and Old Norse:
- Málið.is (Icelandic dictionaries and language resources)
- Netutgafan (classic Norse texts)
- Italian:
- Liber Liber (from Italy)
- Pelagus Letteratura Italiana (searchable index of Italian literature and sites)
- Indian languages:
- Granth Sanjeevani (rare books and other historic materials, many in Indian languages)
- National Digital Library of India (among other languages; registration required)
- Rekhta (poetry in Urdu and other languages)
- Japanese:
- Aozora Bunko (2000+ works of public domain Japanese literature)
- Database of Pre-Modern Japanese Works (from the National Institute of Japanese Literature)
- Japanese Censorship Collection (1000+ works submitted to imperial censors in the early 20th century)
- National Diet Library Digital Collections (hundreds of thousands of digital documents, mostly in Japanese)
- Korean:
- Kawai Collection (digitized Korean classical manuscripts and books)
- National Library of Korea Digitized Materials (mostly in Korean)
- Maori: Maori Niupepa Collection (newspapers written for Maori audience, 1842-1932)
- Mayan: Maya Hieroglyphic Writing: The Ancient Codices
- Polish:
- Staropolska (Old Polish literature)
- Wirtualna Biblioteka Literatury Polskiej (Virtual Library of Polish Literature)
- Portuguese:
- ebooksbrasil (Brazilian literature, mostly Portuguese)
- Jornal de Poesia (Portuguese poetry)
- Literatura Brasileira: Digital Library of Portuguese-Language Literature
- Projecto Vercial (Portuguese authors and literature)
- Romanian:
- Restitutio (digital platform of ‘Carol I’ Central University Library in Bucharest)
- Russian:
- Armenian House Library (Russian section)
- Sanskrit:
- Dvaita Text Resources (classic Hindu texts)
- Reading the Vedic Literature in Sanskrit (at Maharishi University)
- Sanskrit Documents (archive, index, and forum)
- Scandinavian Languages: Project Runeberg (from Sweden)
- Serbian (see also South Slavic Languages): Projekat Rastko (Serbian texts and images)
- Scots/Scottish: Scottish Corpus of Texts and Speech (in the UK; also has English)
- Slovak: Zlatý Fond (in Slovakia)
- Slovenian (see also South Slavic Languages):
- South Slavic languages (see also Serbian, Slovenian, etc.):
- Spanish:
- Biblioteca Virtual Miguel De Cervantes (Spanish texts; JavaScript-dependent)
- CLACSO (social science books in Spanish)
- Elaleph (Spanish-language PDF texts)
- Textos Lemir (medieval Spanish texts)
- Sumerian: Electronic Text Corpus of Sumerian Literature (at Oxford)
- Swahili:
- Syriac: Syriac Studies Reference Library (at BYU; also includes texts in Latin and other languages)
- Tamil:
- Tibetan:
- Buddhist Digital Resource Center (Collection of Buddhist literature, mostly in Tibetan)
- Timeless Treasuries (Tibetan Buddhist literature from the Tsadra Foundation)
- Turkish:
- Uysal-Walker Archive of Turkish Oral Narrative (at Texas Tech)
- Wikilala (digitized Ottoman Turkish documents)
- Ukrainian: Electronic Library of Ukrainian Literature (at Toronto)
- Welsh:
- Llyfrgell Owen (online library of Welsh-language texts)
- National Library of Wales Digital Gallery (online materials in Welsh and English)
- Yiddish:
- Mendele Yiddish Texts
- Yiddish Book Center Digital Yiddish Library (11,000+ titles via archive.org)
- Yizkor Books (Holocaust memorial books; at NYPL)

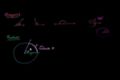 Unit circle definition of trig functions
Unit circle definition of trig functions Graphs of trig functions
Graphs of trig functions Trig identities and examples
Trig identities and examples Linear equations
Linear equations Linear inequalities
Linear inequalities Graphing and analyzing linear functions
Graphing and analyzing linear functions Systems of equations and inequalities
Systems of equations and inequalities Multiplying and factoring expressions
Multiplying and factoring expressions Quadratic equations
Quadratic equations Exponent expressions and equations
Exponent expressions and equations Functions
Functions Ratios and proportions
Ratios and proportions