
Álgebra
Antecedentes de las escuelas de Wikipedia
Esta selección se hace para las escuelas por caridad para niños leer más . Una buena manera de ayudar a otros niños es mediante el patrocinio de un niño
El álgebra es una rama de las matemáticas en relación con el estudio de la estructura , relación y cantidad . El nombre se deriva del tratado escrito en árabe por el Persa matemático, astrónomo, astrólogo y geógrafo, Muhammad bin Musa al-Khwarizmi titulado Kitab al-Jabr wa-l-Muqabala (que significa " Compendio de cálculo por reintegración y comparación "), que proporcionaba operaciones simbólicas para la solución sistemática de lineal y ecuaciones cuadráticas .
Junto con la geometría , el análisis , la combinatoria y teoría de los números , el álgebra es una de las principales ramas de las matemáticas . álgebra elemental es a menudo parte del plan de estudios en la educación secundaria y proporciona una introducción a las ideas básicas de álgebra, incluidos los efectos de la adición y la multiplicación números , el concepto de variables, definición de polinomios , además de factorización y la determinación de su raíces.
El álgebra es mucho más amplio que el álgebra elemental y se puede generalizar. Además de trabajar directamente con los números, álgebra cubre el trabajo con símbolos, variables y conjunto elementos. La suma y la multiplicación son vistos como generales operaciones, y sus definiciones precisas conducen a estructuras tales como grupos , anillos y campos.
Clasificación
Álgebra puede dividirse en las siguientes categorías:
- Álgebra elemental , en el que las propiedades de las operaciones en el sistema de números reales se registran utilizando símbolos como "comodines" para denotar constantes y variables, y las normas que rigen expresiones matemáticas y ecuaciones que involucran estos símbolos son estudiados (nota que este por lo general incluye la materia de cursos llamados álgebra intermedia y álgebra universitaria), también llamado segundo año y tercer año de álgebra;
- Álgebra abstracta , a veces también llamada álgebra moderna, en la que las estructuras algebraicas como grupos , anillos y los campos son axiomáticamente definido e investigado; esto incluye, entre otros campos,
- El álgebra lineal , en el que las propiedades específicas de los espacios vectoriales se estudian (incluyendo matrices );
- Álgebra universal, en el que se estudian las propiedades comunes a todas las estructuras algebraicas.
- Teoría algebraica de números, en la que las propiedades de los números se estudian a través de sistemas algebraicos. Teoría de los números inspiraron gran parte de la abstracción inicial en álgebra.
- La geometría algebraica en su aspecto algebraico.
- Combinatoria algebraica , en la que los métodos algebraicos abstractos se utilizan para estudiar las cuestiones combinatorias.
En algunos sentidos de estudios avanzados, sistemas algebraicos axiomáticos, como grupos, anillos, campos y álgebra sobre un campo se investigan en la presencia de una geométrica estructura (un métrica o una topología ) que es compatible con la estructura algebraica. La lista incluye una serie de áreas de análisis funcional:
- Espacios lineales normados
- Espacios de Banach
- Espacios de Hilbert
- Álgebras de Banach
- Álgebras normado
- Álgebras topológicas
- Grupos topológicos
Álgebra elemental
Álgebra elemental es la forma más básica de álgebra. Se enseña a los estudiantes que se presume que no tienen conocimiento de las matemáticas más allá de los principios básicos de aritmética . En aritmética, sólo los números y sus operaciones aritméticas (como +, -, ×, ÷) ocurrir. En álgebra, los números son a menudo indican mediante símbolos (como A, X, o Y). Esto es útil porque:
- Permite la formulación general de las leyes aritméticas (como a + b = b + a para todo a y b), y por lo tanto es el primer paso para una exploración sistemática de las propiedades del sistema de números reales .
- Permite que la referencia a los números "desconocidos", la formulación de ecuaciones y el estudio de la forma de resolver estos (por ejemplo, "encontrar un número x tal que x 3 + 1 = 10").
- Permite la formulación de funcionales relaciones (tales como "Si usted vende x entradas, entonces su ganancia será de 3 x - 10 dólares, o f (x) = x 3 - 10, donde f es la función y x es el número al que se aplica la función. ").
Polinomios
Un polinomio es una expresión que se construye a partir de uno o más variables y constantes, utilizando sólo las operaciones de suma, resta y multiplicación (donde repitió la multiplicación de la misma variable se forma estándar denotan como exponenciación con un exponente número entero positivo constante). Por ejemplo, 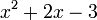 es un polinomio en la única variable x.
es un polinomio en la única variable x.
Una clase importante de problemas en álgebra es la factorización de polinomios, es decir, expresar un polinomio dado como producto de otros polinomios. El ejemplo anterior polinomio se puede factorizar como 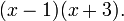 Una clase relacionada de problemas es encontrar expresiones algebraicas para la raíces de un polinomio en una sola variable.
Una clase relacionada de problemas es encontrar expresiones algebraicas para la raíces de un polinomio en una sola variable.
Resumen álgebra
Resumen álgebra extiende los conceptos familiares que se encuentran en el álgebra elemental y la aritmética de los números a los conceptos más generales.
Conjuntos: En lugar de sólo considerar los diferentes tipos de números , ofertas de álgebra abstracta con el concepto más general de conjuntos: una colección de todos los objetos (llamado elementos) seleccionados por la propiedad, específicos para el conjunto. Todas las colecciones de los tipos familiares de los números son conjuntos. Otros ejemplos de conjuntos incluyen el conjunto de todos de dos por dos matrices , el conjunto de todos de segundo grado polinomios (ax 2 + bx + c), el conjunto de todas las dos dimensiones vectores en el plano, y los diversos grupos finitos tales como los grupos cíclicos que son el grupo de números enteros modulo n. La teoría de conjuntos es una rama de la lógica y técnicamente no es una rama del álgebra.
Operaciones binarias: La noción de adición (+) se resumieron para dar una operación binaria *, dicen. La noción de operación binaria no tiene sentido sin el conjunto en el que se define la operación. Durante dos elementos A y B en un conjunto S a * b da otro elemento en el conjunto; esta condición se llama . cierre adición (+), resta (-), multiplicación (×) y división (÷) pueden ser operaciones binarias cuando se define en diferentes conjuntos, como es la suma y la multiplicación de matrices, vectores y polinomios.
Elementos de identidad: Los números cero y uno se abstraen para dar la idea de un elemento de identidad para una operación. Cero es el elemento de identidad para la suma y uno es el elemento de identidad para la multiplicación. Para un operador binario en general * la identidad elemento e debe satisfacer a * e = a y e * a = a. Esto es válido para la adición como + 0 = a y 0 + a = a y multiplicación a × 1 = a y 1 × a = a. Sin embargo, si tomamos los números naturales positivos y además, no hay ningún elemento de identidad.
Elementos inversos: Los números negativos dan lugar al concepto de elementos inversos. Por otra parte, la inversa de una es -a, y para la multiplicación es el inverso 1 / a. Un elemento inverso general, un -1 debe satisfacer la propiedad de que a * a -1 = e y un -1 * a = e.
Asociatividad : La adición de números enteros tiene una propiedad llamada asociatividad. Es decir, la agrupación de los números que se añaden no afecta a la suma. Por ejemplo: (2 + 3) + 4 = 2 + (3 + 4). En general, esto se convierte en (a * b) * c = a * (b * c). Esta propiedad es compartida por la mayoría de las operaciones binarias, pero no la resta o la división o multiplicación Octonión.
Conmutatividad : Adición de números enteros también tiene una propiedad llamada conmutatividad. Es decir, el orden de los números que se añaden no afecta a la suma. Por ejemplo: 2 + 3 = 3 + 2. En general, esto se convierte a * b = b * a. Sólo algunas operaciones binarias tienen esta propiedad. Se mantiene para los enteros con la suma y la multiplicación, pero no se cumple para la multiplicación de matrices o multiplicación de cuaterniones.
Grupos-estructuras de un conjunto con una sola operación binaria
La combinación de los conceptos indicados anteriormente conduce a una de las estructuras más importantes en matemáticas: un grupo . Un grupo es una combinación de un conjunto S y un solo operación binaria "*", que se define de la forma que elija, pero con las siguientes propiedades:
- Un elemento de identidad e existe, tal que para cada miembro de una de S, e * A y A * e son tanto idéntica a una.
- Cada elemento tiene una inversa: para cada miembro de una S, existe un miembro de un -1 tal que a * a -1 y -1 * son un tanto idéntico al elemento de identidad.
- La operación es asociativa: si a, b y c son miembros de S, entonces (a * b) * c es idéntico a un * (b * c).
Si un grupo es también conmutativa - es decir, para cualquiera de los dos miembros a y b de S, a * b es idéntico a B * A - entonces el grupo se dice que es Abeliano.
Por ejemplo, el conjunto de los enteros bajo la operación de adición es un grupo. En este grupo, el elemento de identidad es 0 y la inversa de cualquier elemento a es su negación, - a. El requisito de asociatividad se cumple, porque para cualquier números enteros a, b y c, (a + b) + c = a + (b + c)
Los nulos números racionales forman un grupo bajo la multiplicación. En este caso, el elemento de identidad es 1, desde el 1 × a = a × 1 = a para cualquier número racional a. La inversa de a es 1 / a, ya que a × 1 / a = 1.
Los enteros bajo la operación de multiplicación, sin embargo, no forman un grupo. Esto es porque, en general, el inverso multiplicativo de un número entero no es un entero. Por ejemplo, 4 es un número entero, pero su inverso multiplicativo es 1/4, que no es un entero.
La teoría de grupos es estudiado en la teoría de grupos . Un resultado importante de esta teoría es la clasificación de los grupos finitos simples, publicados en su mayoría entre aproximadamente 1955 y 1983, que se cree para clasificar la totalidad de la finito grupos simples en unos 30 tipos básicos.
| Ejemplos | ||||||||||
| Ajuste: | Números naturales 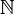 | Enteros 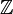 | Numeros racionales 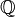 (También verdadero (También verdadero 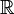 y complejo y complejo 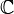 números) números) | Los enteros mod 3: {0,1,2} | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Operación | + | × (w / o cero) | + | × (w / o cero) | + | - | × (w / o cero) | ÷ (w / o cero) | + | × (w / o cero) |
| Cerrado | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí |
| Identidad | 0 | 1 | 0 | 1 | 0 | N / A | 1 | N / A | 0 | 1 |
| Inverso | N / A | N / A | -a | N / A | -a | N / A | 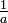 | N / A | 0,2,1, respectivamente | NA, 1, 2, respectivamente |
| De asociación | Sí | Sí | Sí | Sí | Sí | No | Sí | No | Sí | Sí |
| Conmutativa | Sí | Sí | Sí | Sí | Sí | No | Sí | No | Sí | Sí |
| Estructura | monoide | monoide | Grupo abeliano | monoide | Grupo abeliano | cuasigrupo | Grupo abeliano | cuasigrupo | Grupo abeliano | Grupo abeliano ( 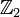 ) ) |
Semigrupos, cuasigrupos, y monoides son estructuras similares a los grupos, pero más general. Comprenden un conjunto y una operación binaria cerrada, pero no necesariamente se cumplen las demás condiciones. La semigrupo tiene una operación binaria asociativa, pero podría no tener un elemento de identidad. La monoide es un semigrupo que no tener una identidad, pero podría no tener un inverso de cada elemento. La cuasigrupo satisface el requisito de que cualquier elemento puede convertirse en cualquier otra por un único pre o post-operación; sin embargo, la operación binaria podría no ser asociativa. Todos son ejemplo de grupoides, las estructuras con una operación binaria en la que no se impongan más condiciones.
Todos los grupos son monoides, y todos monoides son semigrupos.
Anillos y campos-estructuras de un conjunto con dos operaciones binarias particulares, (+) y (x)
Grupos sólo tienen una operación binaria. Para explicar totalmente el comportamiento de los distintos tipos de números, estructuras con dos operadores necesitan ser estudiados. El más importante de éstos son anillos, y campos.
Distributivity generalizó la ley distributiva para los números, y especifica el orden en que se deben aplicar los operadores, (llamado precedencia). Para los números enteros (a + b) × c = a × c + b × c y c × (a + b) = c × a + c × b, y x se dice que es distributiva sobre +.
La anillo tiene dos operaciones binarias (+) y (x), con distributiva × sobre +. Bajo el primer operador (+) forma un grupo abeliano. Bajo el segundo operador (×) es asociativa, pero no necesita tener identidad, o inversa, por lo que la división no está permitido. El elemento neutro de la suma (+) se escribe como 0 y el inverso aditivo de un escrito como - a.
Los enteros son un ejemplo de un anillo. Los enteros tienen propiedades adicionales que hacen que sea un dominio integral.
La campo es un anillo con la propiedad adicional de que todos los elementos excluyendo 0, forman un grupo abeliano bajo ×. La identidad multiplicativa (×) se escribe como 1 y el inverso multiplicativo de un se escribe como un -1.
Los números racionales, los números reales y los números complejos son ejemplos de campos.
Objetos llamadas álgebras
La palabra álgebra también se utiliza para diversas estructuras algebraicas :
- Algebra sobre un campo o más generalmente Álgebra sobre un anillo
- Álgebra sobre un conjunto
- Álgebra de Boole
- F-álgebra y F-coalgebra en teoría de la categoría
- Sigma-álgebra
Historia

Los orígenes del álgebra se remontan a la antigua Babilonios, que desarrollaron un avanzado sistema de aritmética con los que fueron capaces de hacer cálculos en una forma algebraica. Con el uso de este sistema fueron capaces de aplicar fórmulas y calcular soluciones para valores desconocidos para una clase de problemas típicamente resueltos hoy mediante el uso de ecuaciones lineales , ecuaciones cuadráticas , y ecuaciones lineales indeterminadas. Por el contrario, la mayoría Egipcios de esta época, y la mayoría de la India , Griego y Los matemáticos chinos en el primero milenio antes de Cristo, generalmente resuelto por tales ecuaciones geométricas métodos, tales como los descritos en el Papiro matemático de Rhind, Sulba Sutras, los Elementos de Euclides , y Los nueve capítulos en el arte matemático. La obra geométrica de los griegos, tipificado en los Elementos, sirvió de marco para la generalización de las fórmulas más allá de la solución de problemas específicos en los sistemas más generales de afirmar y resolver ecuaciones.
Más tarde, los matemáticos indios desarrollaron métodos algebraicos a un alto grado de sofisticación. Aunque Diofanto y los babilonios usaron métodos principalmente especiales ad hoc para resolver ecuaciones, Brahmagupta fue el primero en resolver ecuaciones usando métodos generales. Él resolvió las ecuaciones indeterminadas lineales, ecuaciones cuadráticas, de segundo orden ecuaciones indeterminadas y ecuaciones con múltiples variables.
La palabra "álgebra" es el nombre del árabe la palabra "al-Jabr" en el título del libro al-Kitab al-muḫtaṣar fî Hisab al-Gabr wa-l-muqabala, que significa El libro de los sumarios de Cálculo por Transposición y Reducción, un libro escrito por el Matemático persa Muhammad ibn Musa al-Khwarizmi en 820. La palabra Al-Jabr significa "reunión". El matemático helenístico Diofanto tradicionalmente se ha conocido como "el padre del álgebra", pero ahora existe un debate en cuanto a si o no Al-Khwarizmi debería tener ese título. Los que apoyan el punto Al-Khwarizmi sobre el hecho de que gran parte de su trabajo en reducción es todavía en uso hoy en día y que ha dado una explicación exhaustiva de la solución de ecuaciones cuadráticas. Los que apoyan Diofanto apuntan al hecho de que el álgebra se encuentra en Al-Jabr es más elemental que el álgebra se encuentra en Aritmética y que Arithmetica es sincopado mientras que Al-Jabr es totalmente retórica. Otro matemático persa, Omar Khayyam, desarrollado geometría algebraica y encontró la solución geométrica general de la ecuación cúbica. Los matemáticos indios Mahavira y Bhaskara II, y el matemático chino Zhu Shijie, resuelto varios casos de cúbico, cuarto grado, quinto grado y de orden superior polinomios ecuaciones.
Otro evento clave en el desarrollo del álgebra fue la solución algebraica general de las ecuaciones de tercer y cuarto grado, desarrollado en el siglo de mid-16th. La idea de un determinante fue desarrollado por Matemático japonés Kowa Seki en el siglo 17, seguido por Gottfried Leibniz diez años después, a los efectos de los sistemas de ecuaciones lineales simultáneas utilizando la solución de matrices . Gabriel Cramer también hizo algunos trabajos sobre matrices y determinantes en el siglo 18. Resumen álgebra fue desarrollado en el siglo 19, centrándose inicialmente en lo que ahora se llama la teoría de Galois , y en cuestiones constructibilidad.
Las etapas del desarrollo del álgebra simbólica son más o menos de la siguiente manera:
- Álgebra retórica, que fue desarrollado por los babilonios y se mantuvo dominante hasta el siglo 16;
- Álgebra geométrica constructiva, que se destacó por la Védicos matemáticos griegos indios y clásicos;
- Álgebra sincopada, como el desarrollado por Diofanto, Brahmagupta y la Bakhshali manuscrito; y
- Álgebra simbólica, que fue iniciado por Abu al-Hasan ibn Ali al-Qalasadi y ve su culminación en la obra de Gottfried Leibniz .

Una cronología de desarrollos algebraicos fundamentales son los siguientes:
- Circa 1800 AC: La Antigua Babilonia Tableta Estrasburgo busca la solución de una ecuación cuadrática elíptica.
- Circa 1600 AC: La Plimpton 322 tableta da una tabla de Ternas pitagóricas en Babilonia Escritura cuneiforme.
- Hacia el año 800 aC: matemático indio Baudhayana, en su Baudhayana Sulba Sutra, descubre ternas pitagóricas algebraicamente, encuentra soluciones geométricas de ecuaciones lineales y ecuaciones de segundo grado de la hacha formas 2 = c y ax 2 + bx = c, y encuentra a dos conjuntos de soluciones integrales positivos a un conjunto de simultánea Ecuaciones diofánticas.
- Hacia el año 600 aC: matemático indio Apastamba, en su Apastamba Sulba Sutra, resuelve la ecuación lineal general y utiliza ecuaciones diofánticas simultáneas con hasta cinco incógnitas.
- Hacia el año 300 aC: En el libro II de sus Elementos, Euclides da una construcción geométrica con herramientas euclidianas para la solución de la ecuación de segundo grado para las raíces reales positivas. La construcción se debe a la escuela pitagórica de la geometría.
- Hacia el año 300 aC: Una construcción geométrica para la solución de la cúbica se busca (duplicando el problema cubo). Ahora es bien conocido que la cúbica general no tiene solución de este tipo usando herramientas euclidianas .
- Hacia el año 100 aC: ecuaciones algebraicas son tratados en el libro de matemáticas chino Jiuzhang suanshu (Los nueve capítulos en el arte matemático), que contiene las soluciones de ecuaciones lineales resolverse utilizando la imperio de la doble posición falsa, soluciones geométricas de ecuaciones de segundo grado, y las soluciones de matrices equivalentes al método moderno, para resolver sistemas de ecuaciones lineales simultáneas.
- Hacia el año 100 aC: El Bakhshali Manuscrito escrito en India antigua utiliza una forma de notación algebraica utilizando letras del alfabeto y otros signos, y contiene las ecuaciones de tercer y cuarto, soluciones algebraicas de ecuaciones lineales con hasta cinco incógnitas, la fórmula algebraica general de la ecuación de segundo grado, y soluciones de ecuaciones cuadráticas indeterminadas y ecuaciones simultáneas.
- Circa 150 AD: Herón de Alejandría trata ecuaciones algebraicas en tres volúmenes de las matemáticas.
- Circa 200: Diofanto, que vivió en Egipto y es a menudo considerado como el "padre del álgebra", escribe su famoso Aritmética, una obra que ofrece soluciones de ecuaciones algebraicas y en la teoría de números.
- 499: matemático indio Aryabhata, en su tratado Aryabhatiya, obtiene soluciones de números enteros a las ecuaciones lineales por un método equivalente a la moderna, describe la solución integral general de la ecuación lineal indeterminado y da soluciones integrales de ecuaciones lineales indeterminadas simultáneas.
- Circa 625: matemático chino Wang Xiaotong encuentra soluciones numéricas de las ecuaciones cúbicas.
- 628: matemático indio Brahmagupta, en su tratado Brahma Sputa Siddhanta, inventa el método chakravala de resolver ecuaciones cuadráticas indeterminadas, incluso La ecuación de Pell, y da reglas para la resolución de ecuaciones lineales y cuadráticas.
- 820: La palabra álgebra se deriva de las operaciones descritas en el tratado escrito por el Matemático persa Muhammad ibn Musa al-Ḵwārizmī titulado Al-Kitab al-Jabr wa-l-Muqabala (que significa "Compendio de cálculo por reintegración y comparación") en la solución sistemática de lineal y ecuaciones cuadráticas . Al-Khwarizmi es a menudo considerado como el "padre del álgebra", gran parte de sus obras en la reducción fue incluido en el libro y se añade a muchos métodos que tenemos en álgebra ahora.
- Circa 850: Matemático persa al-Mahani concibió la idea de reducir problemas geométricos como la duplicación del cubo a problemas de álgebra.
- Circa 850: matemático indio Mahavira resuelve varias ecuaciones cuadráticas, cúbicas, cuarto grado, quinto grado y de orden superior, así como cuadrática indeterminada, ecuaciones cúbicas y de orden superior.
- Circa 990: Persa Abu Bakr al-Karaji, en su tratado al-Fakhri, desarrolla el álgebra al extender la metodología de Al-Khwarizmi incorporar potencias enteras y raíces integrales de cantidades desconocidas. Reemplaza a las operaciones geométricas de álgebra con operaciones aritméticas modernas, y define la monomios x, x 2, x 3, ... y 1 / x, 1 / x 2, 1 / x 3, ... y establece normas para los productos de cualquiera de dos de estos.
- Circa 1050: matemático chino Jia Xian encuentra soluciones numéricas de ecuaciones polinómicas.
- 1072: Matemático persa Omar Khayyam desarrolla la geometría algebraica y, en el Tratado de la demostración de los Problemas de Álgebra, da una clasificación completa de las ecuaciones cúbicas con soluciones geométricas generales que se encuentran a través de la intersección de secciones cónicas.
- 1114: matemático indio Bhaskara, en su Bijaganita (Álgebra), reconoce que un número positivo tiene un aspecto positivo y negativo de la raíz cuadrada , y resuelve varias ecuaciones polinómicas cúbicos, de cuarto grado y de orden superior, así como la ecuación cuadrática indeterminada general.
- 1202: Algebra es introducido en Europa en gran parte gracias a la labor de Leonardo Fibonacci de Pisa en su obra Líber Abad.
- Circa 1300: matemático chino Zhu Shijie ocupa de álgebra polinómica, resuelve ecuaciones cuadráticas, ecuaciones simultáneas y ecuaciones con hasta cuatro incógnitas, y numéricamente resuelve algunos de cuarto grado, quinto grado y de orden superior ecuaciones polinómicas.
- Circa 1400: matemático indio Madhava de Sangamagramma encuentra métodos iterativos para solución aproximada de ecuaciones no lineales.
- Circa 1450: matemático árabe Abu al-Hasan ibn Ali al-Qalasadi tomó "los primeros pasos hacia la introducción de simbolismo algebraico. "Representó símbolos matemáticos utilizando personajes de la Alfabeto árabe.
- 1535: Nicolo Fontana Tartaglia y otros matemáticos en Italia resueltos de forma independiente la ecuación cúbica general.
- 1545: Girolamo Cardano publica Ars magna - El gran arte que da solución de Fontana a la ecuación de cuarto grado general.
- 1572: Rafael Bombelli reconoce las raíces complejas de la cúbica y mejora la notación actual.
- 1591: Francois Viete desarrolla una mejor notación simbólica para diversos poderes de un desconocido y utiliza vocales para las incógnitas y las consonantes para las constantes en En Artem analyticam isagoge.
- 1631: Thomas Harriot en una publicación póstuma usa la notación exponencial y es el primero en utilizar símbolos para indicar "menor que" y "mayor que".
- 1682: Gottfried Wilhelm Leibniz desarrolla su noción de manipulación simbólica con reglas formales que llama characteristica generalis.
- 1680: matemático japonés Kowa Seki, en su método de resolver los problemas disimuladas, descubre el factor determinante , y Números de Bernoulli.
- 1750: Gabriel Cramer, en su tratado Introducción al análisis de las curvas algebraicas, afirma Regla y estudios de Cramer algebraica curvas, matrices y determinantes.
- 1824: Niels Henrik Abel demostró que la ecuación de quinto grado es insoluble por los radicales.
- 1832: la teoría de Galois es desarrollado por Evariste Galois en su trabajo sobre álgebra abstracta.

