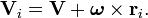Velocidad angular
Antecedentes
SOS cree que la educación da una mejor oportunidad en la vida para los niños en el mundo en desarrollo también. SOS Children ha cuidado de niños en África durante cuarenta años. ¿Puedes ayudar a su trabajo en África ?
- No debe confundirse con frecuencia angular
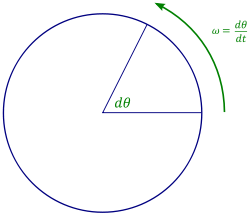
En la física , la velocidad angular es un vector cantidad (más precisamente, una pseudovector) que especifica el la velocidad angular a la que un objeto está girando junto con la dirección en la que está girando. La Unidad SI de velocidad angular es radianes por segundo, aunque puede ser medida en otras unidades como grados por segundo, grados por hora, etc. Cuando se mide en ciclos o revoluciones por unidad de tiempo (por ejemplo, revoluciones por minuto), que a menudo se llama la velocidad de rotación y su magnitud la velocidad rotacional. La velocidad angular generalmente se representa con el símbolo omega (Ω o ω). La dirección del vector de velocidad angular es perpendicular al plano de rotación, en una dirección que por lo general se especifica mediante el regla de la mano derecha.
La velocidad angular de una partícula
Dos dimensiones
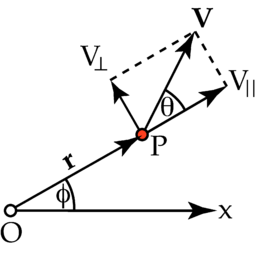
La velocidad angular de una partícula en un plano de 2 dimensiones es la más fácil de entender. Como se muestra en la figura de la derecha (por lo general expresan las medidas angulares φ y θ en radianes ), si trazamos una línea desde el origen (O) a la partícula (P), entonces el vector de velocidad ( 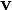 ) De la partícula tendrá un componente a lo largo del radio (
) De la partícula tendrá un componente a lo largo del radio ( 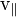 - El componente radial) y un componente perpendicular al radio (
- El componente radial) y un componente perpendicular al radio ( 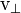 - La componente tangencial).
- La componente tangencial).
Un movimiento radial no produce rotación de la partícula (en relación con el origen), por lo que para los propósitos de encontrar la velocidad angular de la (radial) componente paralela puede ser ignorada. Por lo tanto, la rotación está completamente producido por el movimiento tangencial (como la de una partícula que se mueve a lo largo de una circunferencia), y la velocidad angular se determina completamente por el (tangencial) componente perpendicular.
Se puede observar que la tasa de cambio de la posición angular de la partícula está relacionado con la velocidad tangencial por:
Utilizando θ, el ángulo entre los vectores 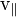 y v, o de forma equivalente como el ángulo entre los vectores r y v, da:
y v, o de forma equivalente como el ángulo entre los vectores r y v, da:
Combinando las dos ecuaciones anteriores y la definición de la velocidad angular ω = ya que los rendimientos dφ / dt:
En dos dimensiones de la velocidad angular es un número único, que no tiene ninguna dirección. Un número único que no tiene sentido es o bien un escalar o una pseudoescalar, con la diferencia de que un escalar no cambia de signo cuando se intercambian los ejes X e Y (o invertida), mientras que un pseudoescalar hace. El ángulo así como la velocidad angular es un pseudoescalar. Se considera que el sentido de giro positivo, por convención, para estar en la dirección hacia el eje y del eje x. Si los ejes están invertidos, pero el sentido de una rotación no, entonces el signo del ángulo de rotación, y por lo tanto la velocidad angular, así, va a cambiar.
Es importante señalar que la velocidad angular pseudoescalar de una partícula depende de la elección del origen y de la orientación de los ejes de coordenadas.
Tres dimensiones
En tres dimensiones, la velocidad angular se vuelve un poco más complicado. La velocidad angular en este caso es generalmente considerado como un vector , o más precisamente, una pseudovector. Ahora tiene no sólo una magnitud, pero una dirección. La magnitud es la velocidad angular, y la dirección se describe la eje de rotación. La regla de la mano derecha indica la dirección positiva del pseudovector velocidad angular, a saber:
- Si usted encrespa los dedos de la mano derecha para seguir la dirección de la rotación, entonces la dirección del vector de velocidad angular se indica con el pulgar derecho.
Así como en el caso bidimensional, una partícula tendrá un componente de su velocidad a lo largo del radio desde el origen a la partícula, y otro componente perpendicular a ese radio. La combinación del punto de origen y el componente de la velocidad perpendicular define un plano de rotación en la que el comportamiento de la partícula (por ese instante) aparece justo como lo hace en el caso bidimensional. El eje de rotación es entonces una línea perpendicular a este plano, y este eje define la dirección de la pseudovector velocidad angular, mientras que la magnitud es el mismo que el valor pseudoescalar encontrado en el caso 2-dimensional. Definir un vector unitario 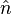 que apunta en la dirección de la pseudovector velocidad angular. La velocidad angular se puede escribir de una manera similar a la de dos dimensiones:
que apunta en la dirección de la pseudovector velocidad angular. La velocidad angular se puede escribir de una manera similar a la de dos dimensiones:
que, por la definición del producto vectorial , se puede escribir:
Dimensiones superiores
En general, la velocidad angular en un espacio n-dimensional es la derivada de tiempo del tensor de desplazamiento angular que es un segundo rango sesgar-simétrica tensor. Este tensor tendrá n (n-1) / 2 componentes independientes y este número es la dimensión de la Acuéstese álgebra de la Grupo de Lie de rotaciones de un espacio n-dimensional del producto interno. Resulta que en el espacio tridimensional velocidad angular puede ser representado por el vector porque el número de componentes independientes es igual al número de dimensiones del espacio.
La velocidad angular de un cuerpo rígido
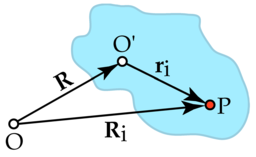
Con el fin de tratar con el movimiento de una cuerpo rígido, lo mejor es considerar un sistema que se fija con respecto al cuerpo rígido de coordenadas, y estudiar las transformaciones de coordenadas entre esta coordenada y el sistema de "laboratorio" fijo. Como se muestra en la figura de la derecha, el origen del sistema de laboratorio es en el punto O, el origen del sistema de cuerpo rígido es en O 'y el vector de O a O' es R. Una partícula (i) en el cuerpo rígido está situado en el punto P y el vector de posición de esta partícula es R i en el marco del laboratorio, y en la posición r i en el bastidor de carrocería. Se ve que la posición de la partícula se puede escribir:
La característica definitoria de un cuerpo rígido es que la distancia entre dos puntos en un cuerpo rígido es invariable en el tiempo. Esto significa que la longitud del vector 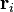 es inmutable. Por Teorema de rotación de Euler, que podrá sustituir al vector
es inmutable. Por Teorema de rotación de Euler, que podrá sustituir al vector 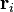 con
con 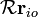 donde
donde 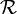 es un matriz de rotación y
es un matriz de rotación y 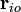 es la posición de la partícula en algún punto fijo en el tiempo, por ejemplo t = 0. Este reemplazo es útil, porque ahora es sólo la matriz de rotación
es la posición de la partícula en algún punto fijo en el tiempo, por ejemplo t = 0. Este reemplazo es útil, porque ahora es sólo la matriz de rotación 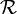 que está cambiando en el tiempo y no el vector de referencia
que está cambiando en el tiempo y no el vector de referencia 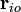 , Ya que el cuerpo rígido gira alrededor del punto O '. La posición de la partícula está escrito como:
, Ya que el cuerpo rígido gira alrededor del punto O '. La posición de la partícula está escrito como:
Tomando la derivada temporal permite la velocidad de la partícula:
donde V i es la velocidad de la partícula (en el marco del laboratorio) y V es la velocidad de O '(el origen del bastidor de carrocería rígida). Desde 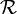 es una matriz de rotación su inversa su su transpuesta. Entonces sustituimos
es una matriz de rotación su inversa su su transpuesta. Entonces sustituimos 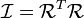 :
:
Continúe tomando el derivitve momento de 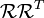 :
:
Aplicando la fórmula (AB) T = B T A T:
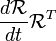 es el negativo de su transpuesta. Por lo tanto, es una matriz 3x3 antisimétrica. Por tanto, podemos tomar su doble para obtener un vector de 3 dimensiones.
es el negativo de su transpuesta. Por lo tanto, es una matriz 3x3 antisimétrica. Por tanto, podemos tomar su doble para obtener un vector de 3 dimensiones. 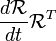 se llama el tensor de velocidad angular . Si tomamos el doble de este tensor, la multiplicación de matrices se sustituye por el producto vectorial. Su doble se llama el pseudovector velocidad angular, ω.
se llama el tensor de velocidad angular . Si tomamos el doble de este tensor, la multiplicación de matrices se sustituye por el producto vectorial. Su doble se llama el pseudovector velocidad angular, ω.
Sustituyendo ω en la expresión velocidad de arriba:
Se puede observar que la velocidad de un punto en un cuerpo rígido se puede dividir en dos términos - la velocidad de un punto de referencia fijo en el cuerpo rígido, más el término producto cruzado que involucra la velocidad angular de la partícula con respecto al punto de referencia . Esta velocidad angular es el "spin" velocidad angular del cuerpo rígido en lugar de la velocidad angular del punto de referencia O 'sobre el origen O.
Es un punto importante que la velocidad angular de giro de cada partícula en el cuerpo rígido es el mismo, y que la velocidad angular de giro es independiente de la elección del origen del sistema de cuerpo rígido o del sistema de laboratorio. En otras palabras, es una cantidad física real, que es una propiedad del cuerpo rígido, independiente de la elección del sistema de coordenadas de uno. La velocidad angular del punto de referencia sobre el origen de la voluntad marco de laboratorio, sin embargo, dependen de estas opciones de sistema de coordenadas. A menudo es conveniente elegir el centro de masa del cuerpo rígido como el origen del sistema de cuerpo rígido, ya que una considerable simplificación matemática se produce en la expresión para el momento angular del cuerpo rígido.


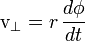
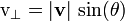
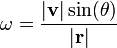
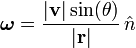
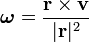
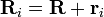
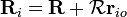
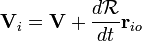
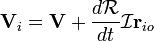
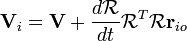
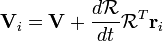
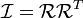
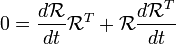
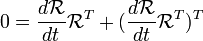
![\ Boldsymbol \ omega = [\ omega_x, \ omega_y, \ omega_z]](../../images/147/14774.png)