
Zona
Sabías ...
Los artículos de esta selección escuelas se han organizado por tema currículo gracias a voluntarios SOS. El apadrinamiento de niños ayuda a los niños uno por uno http://www.sponsor-a-child.org.uk/ .
Area es una cantidad que expresa el dos tamaño dimensional de una parte definida de un superficie, típicamente una región delimitada por una cerrada curva . El área de superficie término se refiere al área total de la superficie expuesta de un sólido de 3 dimensiones, tales como la suma de las áreas de los lados expuestos de un poliedro .
Unidades
Unidades de medida de superficie incluyen:
- Métrico
- metro cuadrado (m²) = Unidades derivadas del Sistema Internacional
- son (a) = 100 metros cuadrados (m²)
- hectárea (ha) = 10.000 metros cuadrados (m²)
- kilómetro cuadrado (km²) = 1.000.000 metros cuadrados (m²)
- Megámetro cuadrado (mm²) = 10 12 metros cuadrados (m²)
- EEUU y Unidades Imperiales
- pie cuadrado = 144 pulgadas cuadradas = 0.09290304 metros cuadrados (m²)
- yarda cuadrada = 9 pies cuadrados = 0.83612736 metros cuadrados (m²)
- cuadrado perca = 30,25 metros cuadrados = 25.2928526 metros cuadrados (m²)
- acre = 160 perchas cuadrados o 4,840 metros cuadrados, o 43.560 pies cuadrados = 4046.8564224 metros cuadrados (m²)
- milla cuadrada = 640 acres = 2,5899881103 kilómetros cuadrados (km²)
Fórmulas útiles
| Forma | Ecuación | Variables |
|---|---|---|
| Cuadrado | 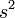 |  es la longitud del lado de la plaza. es la longitud del lado de la plaza. |
| Regular triángulo | 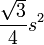 |  es la longitud de un lado del triángulo. es la longitud de un lado del triángulo. |
| Regular hexágono | 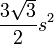 |  es la longitud de un lado del hexágono. es la longitud de un lado del hexágono. |
| Regular octágono | 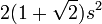 |  es la longitud de un lado del octógono. es la longitud de un lado del octógono. |
| Cualquier polígono regular | 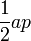 | 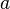 es el apotema, o el radio de un círculo inscrito en el polígono, y es el apotema, o el radio de un círculo inscrito en el polígono, y 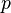 es el perímetro del polígono. es el perímetro del polígono. |
| Cualquier polígono regular | 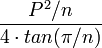 | 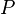 es el perímetro y es el perímetro y 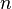 es el número de lados. es el número de lados. |
| Cualquier polígono regular (utilizando medida en grados) | 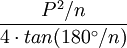 | 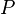 es el perímetro y es el perímetro y 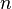 es el número de lados. es el número de lados. |
| Rectángulo | 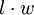 | 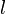 y y 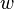 son las longitudes de los lados del rectángulo (longitud y anchura). son las longitudes de los lados del rectángulo (longitud y anchura). |
| Paralelogramo (en general) | 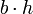 | 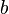 y y 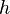 son la longitud de la base y la longitud de la altura perpendicular, respectivamente. son la longitud de la base y la longitud de la altura perpendicular, respectivamente. |
| Rombo | 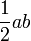 | 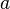 y y 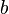 son las longitudes de los dos diagonales del rombo. son las longitudes de los dos diagonales del rombo. |
| Triángulo | 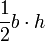 | 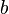 y y 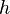 son los base y altitud (medida perpendicular a la base), respectivamente. son los base y altitud (medida perpendicular a la base), respectivamente. |
| Triángulo | 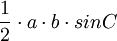 | 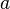 y y 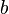 son los dos lados, y son los dos lados, y 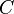 es el ángulo entre ellos. es el ángulo entre ellos. |
| Círculo | 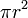 O O 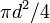 |  es el radio y es el radio y 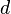 el diámetro . el diámetro . |
| Elipse | 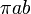 | 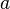 y y 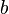 son los semi-mayor y ejes semi-menores, respectivamente. son los semi-mayor y ejes semi-menores, respectivamente. |
| Trapecio | 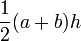 | 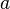 y y 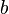 son los lados paralelos y son los lados paralelos y 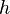 la distancia (altura) entre los paralelos. la distancia (altura) entre los paralelos. |
| Superficie total de una Cilindro | 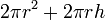 |  y y 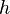 son el radio y la altura, respectivamente. son el radio y la altura, respectivamente. |
| Área de la superficie lateral de un cilindro | 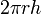 |  y y 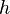 son el radio y la altura, respectivamente. son el radio y la altura, respectivamente. |
| Superficie total de una Cono | 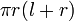 |  y y 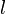 son el radio y altura inclinada, respectivamente. son el radio y altura inclinada, respectivamente. |
| Área de la superficie lateral de un cono | 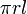 |  y y 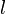 son el radio y la altura inclinada, respectivamente. son el radio y la altura inclinada, respectivamente. |
| Superficie total de una Esfera | 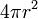 o o 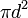 |  y y 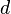 son el radio y el diámetro, respectivamente. son el radio y el diámetro, respectivamente. |
| Superficie total de una elipsoide | Vea el artículo. | |
| Sector circular | 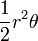 |  y y  son el radio y el ángulo (en radianes ), respectivamente. son el radio y el ángulo (en radianes ), respectivamente. |
| Plaza de conversión de la zona circular | 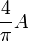 |  es el área de la plaza en unidades cuadradas. es el área de la plaza en unidades cuadradas. |
| Circular cuadrar conversión zona | 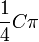 | 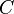 es el área de la círculo en unidades circulares. es el área de la círculo en unidades circulares. |
Todos los cálculos anteriores muestran cómo encontrar el área de muchos formas.


