
Número binario
Antecedentes
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Haga clic aquí para obtener más información sobre SOS Children.
| Sistemas de numeración por la cultura |
|---|
|
| Sistemas posicionales por base |
| Decimal (10) |
| Ternario Balanced |
| Lista de sistemas de numeración |
El sistema de numeración binario, o base-2 sistema de numeración, es un sistema de numeración que representa valores numéricos utilizando dos símbolos, usualmente 0 y 1 . Más específicamente, la habitual basal 2 es un sistema de notación posicional con una radix de 2. Debido a su aplicación directa en circuitos electrónicos, el sistema binario es usado internamente por todos los modernos ordenadores .
Historia
El antiguo escritor indio Pingala desarrolló conceptos matemáticos avanzados para describir prosodia, y al hacerlo, presentó la primera descripción conocida de un sistema de numeración binario, posiblemente ya en el siglo octavo antes de Cristo. Otros lo sitúan mucho más tarde; R. Hall, Matemáticas de la poesía, tiene "c. 200 aC". El sistema de numeración se basa en la Ojo del sistema de numeración Horus Imperio Antiguo.
Un conjunto completo de 8 trigramas y 64 hexagramas, análogos a los números binarios de 3 bits y 6 bits, se sabe que los antiguos chinos en el texto clásico I Ching . Conjuntos similares de combinaciones binarias también se han utilizado en los sistemas de adivinación africanos tradicionales, tales como Ifá así como en Western medieval la geomancia.
Un arreglo binario ordenado de los hexagramas del I Ching, representando la secuencia decimal de 0 a 63, y un método para la generación de la misma, fue desarrollado por el académico y filósofo chino Shao Yong en el siglo 11. Sin embargo, no hay evidencia de que Shao entiende cómputo binario.
En 1605 Francis Bacon discutió un sistema por el cual las letras del alfabeto podrían reducirse a secuencias de dígitos binarios, que luego podrían ser codificados como variaciones apenas visibles en la fuente de cualquier texto aleatorio. Es importante destacar que para la teoría general de la codificación binaria, añadió que este método podría ser utilizado con cualquier objeto en todo: "siempre que esos objetos sean capaces de sólo una diferencia del doble; como por Bells, por Trompetas, por luces y antorchas, por el informe de mosquetes, y de todo instrumento de la misma naturaleza ". (Ver Cifrado de Bacon.)
El sistema numérico binario moderno fue completamente documentado por Gottfried Leibniz en el siglo 17 en su artículo Explicación de l'Arithmétique Binaire . Sistema de Leibniz utiliza 0 y 1, al igual que el sistema de numeración binario moderno.
En 1854, British matemático George Boole publicó un documento histórico que detalla un sistema algebraico de la lógica que sería conocido como Álgebra de Boole. Su cálculo lógico era convertirse en un papel decisivo en el diseño de circuitos electrónicos digitales.
En 1937, Claude Shannon produjo su tesis de maestría en MIT que implementó Álgebra de Boole y aritmética binaria utilizando relés electrónicos e interruptores por primera vez en la historia. Intitulado Un Análisis Simbólico de relé y circuitos de conmutación, la tesis de Shannon básicamente fundó práctico diseño de circuitos digitales.
En noviembre de 1937, George Stibitz, que entonces trabajaba en Laboratorios Bell, completó un equipo basado en relés que llamó el "Modelo K" (por "K itchen", donde se había reunido él), que calcula utilizando la suma binaria. Por tanto, los Laboratorios Bell autorizó un programa de investigación completo a finales de 1938 con Stibitz al timón. Su Complejo Computer Número, completado 8 de enero de 1940 , fue capaz de calcular los números complejos . En una demostración de la Conferencia de la American Mathematical Society en Dartmouth College en 11 de septiembre de 1940 , Stibitz pudo enviar la Calculadora de números complejos comandos remotos a través de líneas telefónicas por un teletipo. Fue la primera máquina de computación utilizado alguna vez de forma remota a través de una línea telefónica. Algunos de los participantes de la conferencia que presenciaron la demostración fueron John Von Neumann , John Mauchly, y Norbert Wiener, quien escribió sobre él en sus memorias.
Representación
Un número binario puede ser representado por cualquier secuencia de los bits (dígitos binarios), que a su vez pueden estar representados por cualquier mecanismo capaz de estar en dos estados mutuamente excluyentes. Las siguientes secuencias de símbolos todos podrían ser interpretadas como el mismo valor numérico binario de 667:
1 0 1 0 0 1 1 0 1 1 | - | - - | | - | | xoxooxxoxx ynynnyynyy
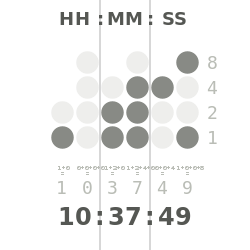
El valor numérico representado en cada caso depende del valor asignado a cada símbolo. En un ordenador, los valores numéricos pueden ser representados por dos diferentes voltajes; en un magnético disco, magnéticos polaridades pueden ser utilizados. Un "positivo", "sí", o "en" estado no es necesariamente equivalente al valor numérico de uno; que depende de la arquitectura en uso.
De acuerdo con la representación habitual de números utilizando números arábigos , números binarios se escriben comúnmente usando los símbolos 0 y 1. Cuando se escribe, los números binarios a menudo se indexan, el prefijo o sufijo para indicar su base o raíz. Las siguientes anotaciones son equivalentes:
- 100101 binario (declaración explícita de formato)
- 100101b (un sufijo que indica formato binario)
- 100101B (un sufijo que indica formato binario)
- bin 100101 (un prefijo que indica formato binario)
- 100.101 2 (un subíndice que indica la base-2 (notación binaria))
- % 100 101 (un prefijo que indica formato binario)
- 0b100101 (un prefijo que indica formato binario, común en los lenguajes de programación)
Cuando se habla, los números binarios se leen normalmente dígito a dígito, con el fin de distinguirlos de los números decimales. Por ejemplo, el número binario 100 se pronuncia uno cero cero, en lugar de cien, para hacer su naturaleza binaria explícita, y para fines de corrección. Desde el binario el número 100 es igual al valor decimal de cuatro, sería confuso, y numéricamente incorrectos, para referirse a los números como cien.
Cuenta en binario
| Binario | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
Cuenta en binario es similar a recuento en cualquier otro sistema numérico. A partir de un solo dígito, contando los ingresos a través de cada símbolo, en orden creciente. Recuento Decimal utiliza los símbolos 0 a 9, mientras el sistema binario sólo utiliza los símbolos 0 y 1.
Cuando se agotan los símbolos para el primer dígito, el inmediatamente superior dígito (a la izquierda) se incrementa, y el conteo comienza de nuevo a 0. En decimal , contando los ingresos, así:
- 000, 001, 002, ... 007, 008, 009, (dígito de la derecha comienza de nuevo y se incrementa al dígito siguiente)
- 0 1 0, 011, 012, ...
- ...
- 090, 091, 092, ... 097, 098, 099, (más a la derecha dos dígitos empezar de nuevo, y se incrementa al dígito siguiente)
- 1 00, 101, 102, ...
Después de un dígito llega a 9, un incremento restablece a 0, pero también provoca un incremento de la cifra siguiente a la izquierda. En binario, la cuenta es la misma, excepto que sólo se utilizan los dos símbolos 0 y 1. Así, después de un dígito alcanza 1 en binario, un incremento restablece a 0, pero también provoca un incremento de la cifra siguiente a la izquierda:
- 000, 001, (dígito de la derecha comienza de nuevo y se incrementa al dígito siguiente)
- 0 1 0, 011, (más a la derecha dos dígitos empezar de nuevo, y se incrementa al dígito siguiente)
- 1 00, 101, ...
Aritmética binaria
La aritmética en binario es muy similar a la aritmética en otros sistemas de numeración. Suma, resta, multiplicación y división se pueden realizar en números binarios.
Adición

La operación aritmética simple en binario es además . Adición de dos números binarios de un dígito es relativamente simple:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (carry: 1)
Adición de dos valores "1" produce el valor "10" (hablado como "uno-cero"), equivalente al valor decimal 2. Esto es similar a lo que ocurre en decimal cuando se suman ciertos números de un solo dígito; si el resultado es igual o excede el valor de la radix (10), el dígito de la izquierda se incrementa:
- 5 + 5 = 10
- 7 + 9 = 16
Esto se conoce como la realización en la mayoría de sistemas de numeración. Cuando el resultado de una adición supera el valor de la radix, el procedimiento es "llevar el uno" a la izquierda, de añadir a la siguiente valor posicional. Llevar las obras de la misma manera en binario:
1 1 1 1 1 (dígitos realizadas)
0 1 0 1 1
+ 1 0 1 1 1
-------------
= 1 0 0 1 0 0
En este ejemplo, se suman dos números: 01101 2 (13 decimal) y 10.111 2 (23 decimal). La fila superior muestra los bits de carry utilizados. A partir de la columna más a la derecha, 1 + 1 = 10 2. La 1 se lleva a la izquierda, y el 0 se escribe en la parte inferior de la columna de la derecha. La segunda columna de la derecha se añade: 1 + 0 + 1 = 10 2 otra vez; el 1 se lleva, y se escribe 0 en la parte inferior. La tercera columna: 1 + 1 + 1 = 11 2 Esta vez, un 1 se lleva, y se escribe 1 en la fila inferior.. Procediendo de esta manera da la respuesta final 100100 2 (36 decimal).
Cuando las computadoras deben sumar dos números, la regla que: x ^ y = x + y 2% para los dos bits de x e y permite el cálculo muy rápido, también.
Sustracción
La resta funciona de la misma manera:
- 0-0 = 0
- 0 - 1 a = 1 (con préstamo)
- 1-0 = 1
- 1 - 1 = 0
Un número binario puede restarse de los otros, como sigue:
* * * * (Columnas con estrellas son tomados de)
1 1 0 1 1 1 0
- 1 0 1 1 1
----------------
= 1 0 1 0 1 1 1
Restar un número positivo es equivalente a la adición de un negativo número de igual valor absoluto ; ordenadores suelen utilizar notación de complemento a dos para representar valores negativos. Esta notación elimina la necesidad de una operación de "sustraer" separada. La sustracción se puede resumir con esta fórmula:
A - B = A + B + 1 no
Para más detalles, consulte complemento a dos.
Multiplicación
Multiplicación en binario es similar a su contraparte decimal. Dos números A y B pueden ser multiplicados por productos parciales: para cada dígito en B, el producto de ese dígito en A se calcula y se escribe en una línea nueva, desplazado hacia la izquierda para que sus líneas más a la derecha de dígitos para arriba con el dígito en B que era utilizado. La suma de todos estos productos parciales da el resultado final.
Puesto que hay sólo dos dígitos en binario, sólo hay dos posibles resultados de cada multiplicación parcial:
- Si el dígito en B es 0, el producto parcial es también 0
- Si el dígito en B es 1, el producto parcial es igual a A
Por ejemplo, los números binarios 1011 y 1010 se multiplican como sigue:
1 0 1 1 (A)
× 1 0 0 1 (B)
---------
0 0 0 0 ← Corresponde a un cero en B
+ 1 0 1 1 ← corresponde a un uno en B
+ 0 0 0 0
+ 1 0 1 1
---------------
= 1 1 0 1 1 1 0
Los números binarios también se pueden multiplicar con pedazos después de un punto binario:
1 0 1,1 0 1 (A) (5.625 en decimal)
× 1 1 0,0 1 (B) (6,25 en decimal)
-------------
1 0 1 1 0 1 ← corresponde a un uno en B
+ 0 0 0 0 0 0 ← Corresponde a un cero en B
+ 0 0 0 0 0 0
+ 1 0 1 0 1 1
+ 1 0 1 0 1 1
-----------------------
= 1 0 0 0 1 1.0 0 1 0 1 (35.15625 en decimal)
Ver también Algoritmo de Booth.
División
Binary división es más similar a su contraparte decimales:
__________
1 0 1 | 1 1 0 1 1
Aquí, el divisor es 101 2 o 5 decimales, mientras que el dividendo es 11 011 2, o 27 decimal. El procedimiento es el mismo que el de decimal división larga; aquí, el divisor 101 2 entra en los primeros tres dígitos 110 2 del dividendo una vez, por lo que un "1" se escribe en la línea superior. Este resultado se multiplica por el divisor, y se resta de los tres primeros dígitos del dividendo; el siguiente dígito (un "1") se incluye para obtener una nueva secuencia de tres dígitos:
1
__________
1 0 1 | 1 1 0 1 1
- 1 0 1
-----
0 1 1
El procedimiento se repite luego con la nueva secuencia, continuando hasta que los dígitos en el dividendo se han agotado:
1 0 1
__________
1 0 1 | 1 1 0 1 1
- 1 0 1
-----
0 1 1
- 0 0 0
-----
1 1 1
- 1 0 1
-----
1 0
Por lo tanto, el cociente de 11,011 2 dividido por 2 101 101 2 es, como se muestra en la línea superior, mientras que el resto, que se muestra en la línea inferior, es 10 2. En decimal, 27 dividido por 5 es 5, con un resto de 2.
Operaciones bit a bit
Aunque no directamente relacionado con la interpretación numérica de símbolos binarios, secuencias de bits pueden ser manipulados utilizando Boolean operadores lógicos. Cuando una cadena de símbolos binarios es manipulada de esta manera, se denomina una operación en modo bit; los operadores lógicos Y, O, y XOR se puede realizar en los bits correspondientes en dos números binarios proporcionados como entrada. La lógica NO operación puede realizarse de bits individuales en un solo número binario proporcionado como entrada. A veces, estas operaciones pueden ser usados como atajos aritméticos, y pueden tener otros beneficios computacionales también. Por ejemplo, una desplazamiento aritmético a la izquierda de un número binario es el equivalente de la multiplicación por un (integral positivo,) potencia de 2.
La conversión hacia y desde otros sistemas de numeración
Decimal
Para convertir de un valor entero de base 10 numeral a su base-2 (binario) equivalente, el número se divide por dos, y el resto es el bit menos significativo. El (integer) resultado se divide de nuevo en dos, su resto es el siguiente bit más significativo. Este proceso se repite hasta que el resultado de un nuevo fraccionamiento se convierte en cero.
Por ejemplo, 118 10, en binario, es decir:
Operación Resto 118 ÷ 2 = 59 0 59 ÷ 2 = 29 1 29 ÷ 2 = 14 1 14 ÷ 2 = 7 0 7 ÷ 2 = 3 1 3 ÷ 2 = 1 1 1 ÷ 2 = 0 1
Lectura de la secuencia de residuos de abajo hacia arriba da el número binario 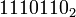 .
.
Este método funciona para la conversión de cualquier base, pero hay mejores métodos para bases que son potencias de dos, como octal y hexadecimal dan a continuación.
Para convertir de base 2 a la base-10 es el algoritmo inverso. A partir de la izquierda, el doble del resultado y añadir el siguiente dígito hasta que no hay más. Por ejemplo, para convertir 110010101101 2 a decimal:
Resultado Dígitos restantes 0 110010101101 0 × 2 + 1 = 1 10010101101 1 × 2 + 1 = 3 0010101101 3 × 2 + 0 = 6 010101101 6 × 2 + 0 = 12 10101101 12 × 2 + 1 = 25 0101101 25 × 2 + 0 = 50 101101 50 × 2 + 1 = 101 01101 101 × 2 + 0 = 202 1101 202 × 2 + 1 = 405 101 405 × 2 + 1 = 811 01 811 × 2 + 0 = 1622 1 1622 × 2 + 1 = 3245
El resultado es 3,245 10.
Binario: 1 1 0 0 1 0 1 0 1 1 0 1
Decimal: [(2 ^ 11) * 1] + [(2 ^ 10) * 1] + [(2 ^ 9) * 0] + [(2 ^ 8) * 0] + [(2 ^ 7) * 1 ] + [(2 ^ 6) * 0] + [(2 ^ 5) * 1] + [(2 ^ 4) * 0] + [(2 ^ 3) * 1] + [(2 ^ 2) * 1 ] + [(2 ^ 1) * 0] + [(2 ^ 0) * 1] = 3245
Las partes fraccionarias de un número se convierten con métodos similares. Se basan más en la equivalencia de desplazamiento con doble o la mitad.
En un número binario fraccional como 0,11010110101 2, el primer dígito es 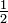 , El segundo
, El segundo 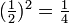 , Etc. Así que si hay un 1 en el primer lugar después del punto decimal, entonces el número es por lo menos
, Etc. Así que si hay un 1 en el primer lugar después del punto decimal, entonces el número es por lo menos 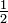 , Y viceversa. Doble que el número es al menos 1. Esto sugiere que el algoritmo: Repetidamente el doble del número que desea convertir, ficha si el resultado es al menos 1, y luego tirar la parte entera.
, Y viceversa. Doble que el número es al menos 1. Esto sugiere que el algoritmo: Repetidamente el doble del número que desea convertir, ficha si el resultado es al menos 1, y luego tirar la parte entera.
Por ejemplo, 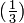 10, en binario, es:
10, en binario, es:
Conversión Resultado 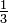
0. 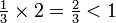
0.0 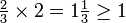
0.01 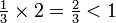
0,010 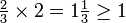
0.0101
Así, la fracción decimal de repetición 0. 3 ... es equivalente a la fracción binaria repitiendo 0. 01 ....
O, por ejemplo, 0,1 10, en binario, es decir:
Conversión Resultado 0.1 0. 0,1 × 2 = 0,2 <1 0.0 0,2 × 2 = 0,4 <1 0.00 0,4 × 2 = 0,8 <1 0.000 0,8 × 2 = 1,6 ≥ 1 0.0001 0,6 × 2 = 1,2 ≥ 1 0.00011 0,2 × 2 = 0,4 <1 0.000110 0,4 × 2 = 0,8 <1 0.0001100 0,8 × 2 = 1,6 ≥ 1 0.00011001 0,6 × 2 = 1,2 ≥ 1 0.000110011 0,2 × 2 = 0,4 <1 0,0001100110
Esto también es una fracción binaria de repetición 0,00011 0011 .... Puede venir como una sorpresa que terminan fracciones decimales pueden tener repiten expansiones en binario. Es por esta razón que muchos se sorprenden al descubrir que 0.1 + ... + 0.1, (10 adiciones) difiere de 1 en aritmética de punto flotante. De hecho, los únicos fracciones binarias con expansiones de terminación son de la forma de un número entero dividida por una potencia de 2, que no es 1/10.
La conversión final es de binario a decimal fracciones. La única dificultad surge con fracciones que se repiten, pero por lo demás el método es cambiar la fracción de un número entero, convertir como anteriormente, y se divide por la potencia apropiada de las dos de la base decimal. Por ejemplo:
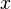
= 1100 .1011100 11100 ... 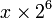
= 1100101110 0.01110 01110 ... 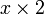
= 11001 0.01110 01110 ... 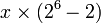
= 1100010101 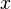
= (789/62) 10
Otra forma de convertir de binario a decimal, a menudo más rápido para una persona familiarizada con hexadecimal , es hacerlo indirectamente, convirtiendo primero ( 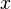 en binario) en (
en binario) en ( 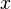 en hexadecimal) y luego la conversión de (
en hexadecimal) y luego la conversión de ( 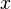 en hexadecimal) en (
en hexadecimal) en ( 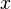 en decimal).
en decimal).
Para números muy grandes, estos métodos simples son ineficientes porque realizan un gran número de multiplicaciones o divisiones donde un operando es muy grande. Un simple algoritmo divide y vencerás es asintóticamente más eficaz: dado un número binario, dividimos por 10 k, donde k se elige de manera que el cociente es igual o menos que el resto, entonces cada una de estas piezas se convierte a decimal y los dos somos concatenada. Dado un número decimal, lo dividimos en dos partes de aproximadamente el mismo tamaño, convertir cada a binario, y luego multiplicar la primera pieza de 10 k y añadirlos, donde k es el número de dígitos en el menos significativo (más a la derecha) pieza .
Hexadecimal
Binary se puede convertir desde y hacia hexadecimal algo más fácilmente. Esto es debido al hecho de que la radix del sistema hexadecimal (16) es una potencia de la radix del sistema binario (2). Más específicamente, 16 = 2 4, por lo que lleva cuatro dígitos de binarios para representar un dígito hexadecimal.
La siguiente tabla muestra cada dígito hexadecimal junto con el valor decimal equivalente y secuencia binaria de cuatro dígitos:
|
|
|
|
Para convertir un número hexadecimal en su equivalente binario, simplemente sustituir los correspondientes dígitos binarios:
- 3A 16 = 0011 1010 2
- E7 16 = 1110 0111 2
Para convertir un número binario en su equivalente hexadecimal, dividirlo en grupos de cuatro bits. Si el número de bits no es un múltiplo de cuatro, simplemente inserte adicionales 0 bits a la izquierda (llamado relleno). Por ejemplo:
- 01010010 2 = 0101 0010 agrupado con relleno = 52 16
- 11011101 = 2 1101 1101 agrupados = DD 16
Para convertir un número hexadecimal en su equivalente decimal, multiplique el equivalente decimal de cada dígito hexadecimal por el poder correspondiente de 16 y agregar los valores resultantes:
- C0E7 16 = (12 × 16 3) + (0 × 16 2) + (14 × 16 1) + (7 × 16 0) = (12 x 4096) + (0 × 256) + (14 × 16) + ( 7 × 1) = 49383 10
Octal
Binary también se puede convertir fácilmente a la sistema de numeración octal, ya octal utiliza un radix de 8, que es una potencia de dos (es decir, 2 3, por lo que toma exactamente tres dígitos binarios para representar un dígito octal). La correspondencia entre octal y los números binarios es el mismo que para los ocho primeros dígitos de hexadecimal en la tabla anterior. Binary 000 es equivalente al dígito octal 0, binario 111 es equivalente a octal 7, y así sucesivamente.
Octal Binario 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111
La conversión de octal a binario procede de la misma manera como lo hace para hexadecimal :
- 65 = 8 110 101 2
- 17 = 8 001 111 2
Y de binario a octal:
- 101 100 2 101 100 2 = agrupados = 54 8
- 10011 = 2 010 011 2 agrupado con relleno = 23 8
Y a partir de octal a decimal:
- 65 8 = (6 × 8 1) + (5 x 8 0) = (6 × 8) + (5 x 1) = 53 10
- 127 8 = (1 × 8 2) + (2 × 8 1) + (7 × 8 0) = (1 × 64) + (2 × 8) + (7 × 1) = 87 10
En representación de los números reales
No enteros se pueden representar mediante el uso de potencias negativas, que se establecen fuera de los otros dígitos por medio de una punto de base (llamado punto decimal en el sistema decimal). Por ejemplo, el número binario 11,01 2 por lo tanto significa:
1 × 2 1 (1 × 2 = 2) más 1 × 2 0 (1 × 1 = 1) más 0 × 2 -1 (0 × ½ = 0) más 1 × 2 -2 (1 × ¼ = 0,25)
Para un total de 3,25 decimal.
Todos números racionales diádicas 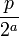 tener una representación binaria del número binario de terminación tiene un número finito de términos después de la coma de la base. Otros números racionales tienen representación binaria, pero en lugar de terminación, que se repiten, con una secuencia finita de dígitos repetir indefinidamente. Por ejemplo
tener una representación binaria del número binario de terminación tiene un número finito de términos después de la coma de la base. Otros números racionales tienen representación binaria, pero en lugar de terminación, que se repiten, con una secuencia finita de dígitos repetir indefinidamente. Por ejemplo
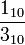 =
= 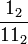 = 0.01010101 01 ... 2
= 0.01010101 01 ... 2
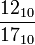 =
= 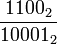 = 0.10110100 10110100 10110100 ... 2
= 0.10110100 10110100 10110100 ... 2
El fenómeno de que la representación binaria de cualquier racional es ya sea de terminación o recurrente también se produce en otros sistemas de numeración basada en Radix. Véase, por ejemplo, la explicación en decimal . Otra similitud es la existencia de representaciones alternativas para cualquier representación de terminación, basándose en el hecho de que 0.111111 ... es la suma de la serie geométrica 2 -1 -2 + 2 + 2 + -3 ... que es 1.
Los números binarios que no terminan ni se repiten representar números irracionales . Por ejemplo,
- 0,10100100010000100000100 .... tiene un patrón, pero no es un patrón recurrente de longitud fija, por lo que el número es irracional
- 1,0110101000001001111001100110011111110 ... es la representación binaria de
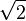 , La raíz cuadrada de 2, otro irracional. No tiene ningún patrón discernible, aunque una prueba de que
, La raíz cuadrada de 2, otro irracional. No tiene ningún patrón discernible, aunque una prueba de que 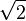 es irracional requiere algo más que esto. Ver número irracional .
es irracional requiere algo más que esto. Ver número irracional .

