Carl Friedrich Gauss

Carl Friedrich Gauss
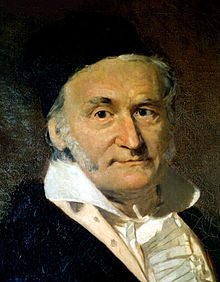Carl Friedrich Gauss (1777-1855), pintado por C. A. Jensen
Nacido	(04/30/1777) 30 de abril 1777 Braunschweig, Ducado de Brunswick-Wolfenbüttel, Sacro Imperio Romano
Murió	23 de febrero 1855 (02/23/1855) (77 años) Göttingen, Reino de Hannover
Residencia	Reino de Hannover
Nacionalidad	Alemán
Campos	Matemáticas y Física
Instituciones	Universidad de Göttingen
Alma máter	Universidad de Helmstedt
Doctoral consejero	Johann Friedrich Pfaff
Otros asesores académicos	Johann Christian Martin Bartels
Los estudiantes de doctorado	Friedrich Bessel Christoph Gudermann Christian Ludwig Gerling Richard Dedekind Johann Encke Johann Ficha Bernhard Riemann Cristiano Peters Moritz Cantor
Otros alumnos notables	Johann Dirichlet Ferdinand Eisenstein Carl Wolfgang Benjamin Goldschmidt Gustav Kirchhoff Ernst Kummer August Ferdinand Möbius LC Schnürlein Julius Weisbach
Conocido por	Ver la lista completa
Influenciado	Sophie Germain
Premios notables	Medalla Copley (1838)
Firma

Johann Carl Friedrich Gauss (pron .: / ɡ aʊ s /; alemán : Gauss, que se pronuncia [ɡaʊs]; América : Carolus Fridericus Gauss) (30 abril 1777 hasta 23 febrero 1855) fue un Alemán matemático y científico físico que han contribuido significativamente a muchos campos, incluida la teoría de números , álgebra , estadísticas , análisis , geometría diferencial , geodesia, geofísica, electrostática, la astronomía y la óptica .

Algunas veces conocido como el mathematicorum Princeps ( América , "el príncipe de los matemáticos" o "el más importante de los matemáticos") y "el matemático más grande desde la antigüedad", Gauss tuvo una influencia notable en muchos campos de las matemáticas y la ciencia, y está considerado como uno de los matemáticos más influyentes de la historia. Se refirió a las matemáticas como "la reina de las ciencias".

Los primeros años (1777-1798)

Estatua de Gauss en su lugar de nacimiento, Braunschweig

Carl Friedrich Gauss nació el 30 de abril 1777 en Braunschweig (Brunswick), en el Ducado de Brunswick-Wolfenbüttel, ahora parte de Baja Sajonia, Alemania , como el hijo de padres pobres de la clase trabajadora. De hecho, su madre era analfabeta y nunca registró la fecha de su nacimiento, recordando sólo que él había nacido en un miércoles, ocho días antes de la Fiesta de la Ascensión, que a su vez se produce 40 días después de Pascua . Gauss más tarde resolver este rompecabezas sobre su fecha de nacimiento en el contexto de encontrar la fecha de la Pascua, que derivan los métodos para calcular la fecha en los dos años pasados y futuros. Fue bautizado y confirmado en una iglesia cerca de la escuela que asistió cuando era niño.

Gauss fue una niño prodigio. Hay muchas anécdotas acerca de su precocidad, mientras que un niño pequeño, y él hizo sus primeros descubrimientos matemáticos innovadores cuando todavía era un adolescente. Completó Disquisitiones Arithmeticae, su opus magnum, en 1798 a la edad de 21, aunque no se publicó hasta 1801. Este trabajo fue fundamental en la consolidación de la teoría de números como disciplina y ha dado forma al campo hasta la actualidad.

Habilidades intelectuales de Gauss atrajeron la atención de la Duque de Brunswick, que lo envió a la Collegium Carolinum (ahora Technische Universität Braunschweig), a la cual asistió desde 1792 hasta 1795, y para el Universidad de Gotinga desde 1795 a 1798. Mientras que en la universidad, Gauss redescubrió independientemente varios teoremas importantes; su gran avance se produjo en 1796 cuando demostró que cualquier regular de polígono con un número de lados que es una Fermat primer (y, en consecuencia, dichos polígonos con cualquier número de lados que es el producto de los números primos de Fermat distintos y una potencia de 2) puede ser construido por compás y una regla . Este fue un gran descubrimiento en un importante campo de las matemáticas; problemas de construcción habían ocupado los matemáticos desde los tiempos de los antiguos griegos , y el descubrimiento de Gauss en última instancia condujo a elegir las matemáticas en lugar de filología como una carrera. Gauss estaba tan contento por este resultado que él pidió que un habitual heptadecágono ser inscrito en su lápida. La cantero se negó, afirmando que la construcción difícil sería esencialmente parecer un círculo.

El año 1796 fue muy productivo para ambos Gauss y la teoría de números. Descubrió una construcción del heptadecágono el 30 de marzo. Avanzó más aritmética modular , lo que simplifica enormemente las manipulaciones en la teoría de números. El 8 de abril se convirtió en el primero en probar la ley de reciprocidad cuadrática. Esta ley muy general, permite a los matemáticos para determinar la solvencia de cualquier ecuación de segundo grado en la aritmética modular. La teorema del número primo, conjeturó el 31 de mayo, da una buena comprensión de cómo los números primos se distribuyen entre los enteros. Gauss también descubrió que cada número entero positivo es representable como una suma de a lo sumo tres números triangulares en 10 de julio y luego anotó en su diario la famosa nota: " ΕΥΡΗΚΑ! num = Δ + Δ + Δ ". El 1 de octubre se publicó el resultado en el número de soluciones de polinomios con coeficientes en campos finitos, que 150 años más tarde dieron lugar a la Conjeturas de Weil.

Año Media (1799-1830)

En su 1799 el doctorado en rebeldía, una nueva demostración del teorema de que cada función algebraica racional integral de una variable se puede descomponer en factores reales del primer o segundo grado, Gauss demostró el teorema fundamental del álgebra que establece que todos los de una sola variable no constante polinomio con coeficientes complejos tiene al menos un complejo raíz. Los matemáticos incluidos Jean le Rond d'Alembert había producido falsas pruebas antes de él, y la disertación de Gauss contiene una crítica de la obra de d'Alembert. Irónicamente, según los estándares de hoy en día, el propio intento de Gauss no es aceptable, debido al uso implícito de la Teorema de la curva de Jordan. Sin embargo, posteriormente se produjo otras tres pruebas, la última en 1849 siendo generalmente rigurosa. Sus intentos aclararon el concepto de los números complejos considerablemente a lo largo del camino.

Gauss también hizo importantes contribuciones a la teoría de números , con su libro 1801 Disquisitiones Arithmeticae ( América , aritméticos Investigaciones), que, entre cosas, introdujo el símbolo ≡ de congruencia y la utilizó en una presentación limpia de la aritmética modular , contenía las dos primeras pruebas de la ley de reciprocidad cuadrática, desarrolló las teorías de binarios y ternarios formas cuadráticas, afirmó el problema número de clase para ellos, y demostró que un habitual heptadecágono (polígono de 17 lados) se puede construir con regla y compás .

Portada de Gauss Disquisitiones Arithmeticae

En ese mismo año, italiano astrónomo Giuseppe Piazzi descubrió el planeta enano Ceres . Piazzi sólo podía rastrear Ceres durante unos meses, después de que durante tres grados a través del cielo nocturno. Luego desapareció temporalmente detrás del resplandor del Sol Varios meses más tarde, cuando Ceres deberían haber vuelto a aparecer, Piazzi no pudo localizarlo: las herramientas matemáticas de la época no eran capaces de extrapolar una posición de una cantidad tan escasa de datos en tres grados representan menos del 1% de la órbita total.

Gauss, quien tenía 23 años en ese momento, se enteró del problema y lo abordó. Después de tres meses de intenso trabajo, predijo una posición de Ceres en diciembre 1801, justo un año después de su primer avistamiento, y esto resultó ser una precisión de medio grado cuando fue redescubierto por Franz Xaver von Zach, el 31 de diciembre a las Gotha, y un día más tarde por Heinrich Olbers en Bremen.

Método de Gauss involucrado determinar una sección cónica en el espacio, dado uno de los focos (el Sol) y la intersección de la cónica con tres líneas dadas (líneas de visión desde la Tierra, la cual es a su vez de pasar una elipse, con el planeta) y dado el tiempo que toma el planeta para atravesar los arcos determinados por estas líneas (de la cual las longitudes de los arcos pueden ser calculados por la Segunda Ley de Kepler). Este problema conduce a una ecuación de la octavo grado, de las cuales una solución, la órbita de la Tierra, es conocido. La solución buscada se separa entonces de los seis restantes en base a las condiciones físicas. En este trabajo de Gauss utilizó métodos integrales de aproximación que él creó para ese fin.

Uno de estos métodos fue el transformada rápida de Fourier. Si bien este método se atribuye tradicionalmente a un papel de 1965 por JW Cooley y JW Tukey, Gauss desarrolló como un método de interpolación trigonométrica. Su papel, Theoria Interpolationis Methodo Nova Tractata, sólo se publicó póstumamente en el volumen 3 de sus obras completas. Este documento es anterior a la primera presentación de Joseph Fourier sobre el tema en 1807.

Zach señaló que "sin el trabajo inteligente y cálculos del doctor Gauss podríamos no haber encontrado Ceres de nuevo". Aunque Gauss tenía hasta ese momento ha apoyado financieramente por su estipendio del duque, dudaba de la seguridad de este acuerdo, y también no creer matemáticas puras sean lo suficientemente importante como para merecer el apoyo. Así que buscó una posición en la astronomía, y en 1807 fue nombrado profesor de astronomía y director del astronómica observatorio de Gotinga, cargo que ocupó durante el resto de su vida.

El descubrimiento de Ceres llevó Gauss a su trabajo en una teoría del movimiento de planetoides perturbado por planetas grandes, publicado finalmente en 1809 como Theoria motus corporum coelestium en sectionibus conicis Solem Ambientum (Teoría del movimiento de los cuerpos celestes se mueven en las secciones cónicas en todo el Sol). En el proceso, por lo que agilizó las matemáticas engorrosos de predicción orbital siglo 18 que su obra sigue siendo una piedra angular de cálculo astronómico. Introdujo la Constante gravitacional gaussiana, y contenía un tratamiento influyente del método de mínimos cuadrados , un procedimiento utilizado en todas las ciencias a este día para minimizar el impacto de error de medición. Gauss demostró el método bajo el supuesto de distribución normal errores (ver Teorema de Gauss-Markov; ver también Gaussian). El método ha sido descrito anteriormente por Adrien-Marie Legendre en 1805, pero Gauss afirmaron que había estado usando desde 1795.

Retrato de Gauss publicó en Astronomische Nachrichten 1828

En 1818 Gauss, poniendo sus habilidades de cálculo para el uso práctico, llevó a cabo un encuesta geodésica de la Reino de Hannover, la vinculación con anteriores daneses encuestas. Para ayudar a la encuesta, Gauss inventó el heliotropo, un instrumento que utiliza un espejo para reflejar la luz del sol a través de grandes distancias, para medir posiciones.

Gauss también afirmó haber descubierto la posibilidad de geometrías no euclidianas, pero nunca lo publicó. Este descubrimiento fue un importante cambio de paradigma en las matemáticas, ya que liberó a los matemáticos de la creencia errónea de que los axiomas de Euclides eran la única manera de hacer que la geometría consistente y no contradictoria. La investigación sobre estas geometrías llevó a, entre otras cosas, Einstein la teoría de la relatividad general, que describe el universo como no euclidiana 's. Su amigo Farkas Wolfgang Bolyai con la que Gauss había jurado "hermandad y la bandera de la verdad" como estudiante, había intentado en vano durante muchos años para demostrar el postulado de las paralelas de otros axiomas de Euclides de la geometría. El hijo de Bolyai, János Bolyai, descubrió la geometría no euclidiana en 1829; su trabajo fue publicado en 1832. Después de verla, Gauss escribió a Farkas Bolyai: "Para decir lo ascendería a alabar a mí mismo por todo el contenido de la obra ... coincide casi exactamente con mis propias meditaciones que han ocupado mi mente. los últimos treinta o treinta y cinco años ".

Cuatro distribuciones gaussianas en estadísticas

Esta afirmación no demostrada poner una tensión en su relación con János Bolyai (que pensaban que Gauss estaba "robando" su idea), pero ahora generalmente se toma en serio. Las cartas de Gauss años antes 1829 revelan él oscuramente discutir el problema de líneas paralelas. Waldo Dunnington, un biógrafo de Gauss, argumenta en Gauss, Titán de la Ciencia que Gauss fue, de hecho, en plena posesión de la geometría no euclidiana mucho antes de ser publicado por János Bolyai, pero que él se negó a publicar nada de eso debido a su temor a la controversia.

La encuesta de Hanover alimentado el interés de Gauss en la geometría diferencial , un campo de las matemáticas que se ocupan de las curvas y superficies. Entre otras cosas, se le ocurrió la idea de Curvatura gaussiana. Esto llevó en 1828 a un importante teorema, la Teorema Egregium (notable teorema), estableciendo una propiedad importante de la noción de curvatura. Informalmente, el teorema dice que la curvatura de una superficie puede ser totalmente determinado por la medición de ángulos y distancias en la superficie. Es decir, la curvatura no depende de cómo podría ser la superficie incrustado en el espacio de 3 dimensiones o espacio de 2 dimensiones.

En 1821, fue nombrado miembro extranjero de la Real Academia Sueca de las Ciencias.

Años posteriores y muerte (1831-1855)

Daguerrotipo de Gauss en su lecho de muerte, 1855.

La tumba de Gauss en Albanifriedhof en Göttingen, Alemania .

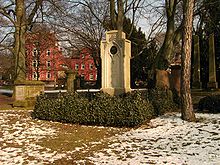
En 1831 Gauss desarrolló una fructífera colaboración con el profesor de física Wilhelm Weber, para obtener nuevos conocimientos en el magnetismo (incluida la búsqueda de una representación de la unidad del magnetismo en términos de masa, longitud y tiempo) y el descubrimiento de Leyes de Kirchhoff de la electricidad. Fue durante este tiempo que él formuló su tocayo ley . Construyeron la primera telégrafo electromecánico en 1833, que conecta el observatorio con el instituto de física en Göttingen. Gauss ordenó una magnética observatorio que se construirá en el jardín del observatorio, y con Weber fundó la "Magnetischer Verein" (Club magnético en alemán ), que apoyó las mediciones del campo magnético de la Tierra en muchas regiones del mundo. Desarrolló un método de medición de la intensidad horizontal del campo magnético que estaba en uso hasta bien entrada la segunda mitad del siglo 20, y elaboró la teoría matemática para separar el interior y exterior ( magnetosférica) fuentes de campo magnético de la Tierra.

En 1840, Gauss publicó su influyente Dioptrische Untersuchungen, en la que dio el primer análisis sistemático de la formación de imágenes bajo un aproximación paraxial ( La óptica de Gauss). Entre sus resultados, Gauss mostró que bajo una aproximación paraxial un sistema óptico puede ser caracterizado por su puntos cardinales y que derivan de la fórmula para la lente de Gauss.

En 1854, Gauss especialmente seleccionado el tema de Bernhard Riemann ya famoso Habilitationvortrag 's, Über die Hypothesen, welche der Geometrie zu Grunde liegen. En el camino a casa de la conferencia de Riemann, Weber informó que Gauss se deshizo en elogios y entusiasmo.

Gauss murió en Göttingen, en el Reino de Hannover (ahora parte de Baja Sajonia, Alemania) en 1855 y está enterrado en el Albanifriedhof cementerio allí. Dos individuos dieron elogios en su funeral: Gauss del hijo-en-ley Heinrich Ewald y Wolfgang Sartorius von Waltershausen, que era íntimo amigo y biógrafo de Gauss. Su cerebro fue preservado y fue estudiado por Rudolf Wagner quien encontró su masa sea 1.492 gramos y la zona cerebral igual a 219588 milímetros cuadrados (340.362 pulgadas cuadradas). También se encontraron circunvoluciones altamente desarrollados, que a principios del siglo 20 fue sugerido como explicación de su genio.

Religión

Bühler escribe que, según la correspondencia con Rudolf Wagner, Gauss no parece creer en un dios personal. Se decía que era ser un deísta. Afirma, además, que aunque Gauss creía firmemente en la inmortalidad del alma y en algún tipo de vida después de la muerte, no fue de una manera que se podría interpretar como cristiano.

Según Dunnington, la religión de Gauss se basa en la búsqueda de la verdad. Creía en "la inmortalidad de la individualidad espiritual, en una permanencia personal después de la muerte, en una última orden de cosas, en un eterno, justo, omnisciente y omnipotente Dios". Gauss también confirmó la tolerancia religiosa, creyendo mal molestar a otras personas que estaban en paz con sus propias creencias.

Familia

Hija de Gauss Teresa (1816-1864)

La vida personal de Gauss se vio ensombrecida por la temprana muerte de su primera esposa, Johanna Osthoff, en 1809, pronto seguido por la muerte de un hijo, Louis. Gauss se sumergió en un depresión de la que nunca se recuperó completamente. Se casó de nuevo, para el mejor amigo de Johanna llamado Friederica Wilhelmine Waldeck pero comúnmente conocido como Minna. Cuando su segunda esposa murió en 1831 tras una larga enfermedad, una de sus hijas, Teresa, se hizo cargo de la casa y asistidos Gauss hasta el final de su vida. Su madre vivía en su casa desde 1817 hasta su muerte en 1839.

Gauss tuvo seis hijos. Con Johanna (1780-1809), sus hijos eran Joseph (1806-1873), Guillermina (1808-1846) y Louis (1809-1810). De todos los hijos de Gauss, Wilhelmina se decía que había llegado más cerca de su talento, pero ella murió joven. Con Minna Waldeck también tuvo tres hijos: Eugene (1811-1896), Wilhelm (1813-1879) y Teresa (1816-1864). Eugene compartió una buena medida del talento de Gauss en idiomas y computación. Teresa mantuvo casa de Gauss hasta su muerte, después de lo cual se casó.

Gauss llegó a tener conflictos con sus hijos. Él no quiere que ninguno de sus hijos para entrar en las matemáticas o la ciencia para el "miedo de bajar el nombre de la familia". Gauss quería Eugene se convierta en un abogado, pero Eugene quería estudiar idiomas. Tuvieron una discusión por una parte Eugene sostuvo, que Gauss se negó a pagar. El hijo dejó en cólera y, en aproximadamente 1832, emigró a los Estados Unidos, donde tuvo bastante éxito. Wilhelm también se estableció en Missouri, comenzando como un agricultor y más tarde llegar a ser ricos en el negocio de zapatos en San Luis. Tomó muchos años para el éxito de Eugene para contrarrestar su reputación entre sus amigos y colegas de Gauss. Ver también la carta de Robert Gauss a Felix Klein en 03 de septiembre 1912.

Personalidad

Gauss fue un ardiente perfeccionista y trabajador. Nunca fue un escritor prolífico, negándose a publicar el trabajo que él no se consideraba completa y por encima de la crítica. Esto está en consonancia con su lema personal pauca matura sed ("pocos, pero madura"). Sus diarios personales indican que él había hecho varios importantes descubrimientos matemáticos años o décadas antes de sus contemporáneos su publicación. Historiador Matemática Eric Temple Bell estimado que, si Gauss publicó todos sus descubrimientos en el momento oportuno, se habría avanzado matemáticas por cincuenta años.

A pesar de que tardó en unos pocos estudiantes, Gauss era conocido que no les gusta la enseñanza. Se dice que asistió a una sola conferencia científica, que se encontraba en Berlín en 1828. Sin embargo, varios de sus estudiantes se convirtieron en matemáticos influyentes, entre ellos Richard Dedekind, Bernhard Riemann , y Friedrich Bessel. Antes de morir, Sophie Germain fue recomendado por Gauss para recibir su título honorario.

Gauss generalmente se negó a presentar la intuición detrás de sus a menudo muy elegantes pruebas-que los prefería a aparecer "de la nada" y borró todo rastro de la forma en que los descubrió. Esto se justifica, si insatisfactoriamente, por Gauss en su " Disquisitiones Arithmeticae ", donde afirma que todos los análisis (es decir, los caminos uno viajó para llegar a la solución de un problema) debe ser suprimida por razones de brevedad.

Gauss apoyó la monarquía y se opuso a Napoleón , a quien veía como una consecuencia de la revolución .

Anécdotas

Hay varias historias de su genio precoz. De acuerdo a uno, sus dones se hizo muy evidente a la edad de tres años cuando se corrigió, mental y sin culpa en sus cálculos, un error que su padre había hecho en papel, mientras que el cálculo de las finanzas.

Otra famosa historia cuenta que en la escuela primaria después de que el joven Gauss se portaba mal, su maestro, JG Büttner, le dio una tarea: añadir una lista de números enteros en progresión aritmética; ya que la historia es más a menudo dijo, estos fueron los números del 1 al 100. El joven Gauss produjo supuestamente la respuesta correcta en cuestión de segundos, ante el asombro de su maestro y su asistente Martin Bartels.

Presunto método de Gauss fue darse cuenta de que la adición de pares de términos de los extremos opuestos de la lista cedió idénticas sumas intermedias: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, y así sucesivamente, por una suma total de 50 × 101 = 5050. Sin embargo, los detalles de la historia son, en el mejor incierta (ver para la discusión del original Fuente Wolfgang Sartorius von Waltershausen y los cambios en otras versiones); algunos autores, como Joseph Rotman en su libro Un primer curso de álgebra abstracta, se preguntan si es que alguna vez ocurrió.

Según Isaac Asimov , Gauss fue una vez interrumpido en medio de un problema y dijo que su esposa estaba muriendo. Él está supuestamente dijo, "Dile que espere un momento hasta que he terminado." Esta anécdota se discute brevemente en Gauss de G. Waldo Dunnington, Titán de la Ciencia, donde se sugiere que se trata de una apócrifa historia.

Conmemoraciones

Alemán 10- Deutsche Marcos de billetes (1993; descontinuado) con Gauss

Gauss (envejeció sobre 26) en Alemania del Este sello producido en 1977. Junto a él: heptadecágono, compás y una regla .

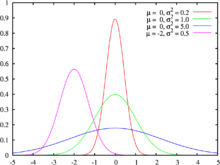
Desde 1989 hasta 2001, el retrato de Gauss, una curva de distribución normal y algunos prominentes Edificios Göttingen fueron presentados en el alemán de diez marcos de billetes. En el reverso aparece el heliotropo y un enfoque de triangulación para Hannover. Alemania también ha emitido tres sellos en honor de Gauss. Uno (n. ° 725) apareció en 1955 en el centenario de su muerte; otros dos, nos. 1246 y 1811, en 1977, el 200 aniversario de su nacimiento.

2005 la novela de Daniel Kehlmann Die Welt der Vermessung, traducida al Inglés como La medición del mundo (2006), explora la vida de Gauss y trabajar a través de una lente de ficción histórica, contrastándolas con las del explorador alemán Alexander von Humboldt.

En 2007, un busto de Gauss se colocó en el Templo Walhalla.

Cosas que llevan el nombre de Gauss incluyen:

• La desmagnetización, el proceso de eliminación de un campo magnético.
• La CGS unidad para campo magnético fue nombrado gauss en su honor,
• El cráter Gauss en la Luna ,
• Asteroide 1001 Gaussia,
• El barco Gauss, utilizado en el Gauss expedición a la Antártida,
• Gaussberg, un volcán extinto descubierto por la expedición mencionado,
• Gauss Tower, una torre de observación en Dransfeld, Alemania ,
• En las escuelas secundarias canadienses, un concurso de matemáticas nacional anual (Gauss Matemáticas Competencia) administrado por el Centro para la Educación en Matemáticas y Computación se nombra en honor de Gauss,
• En Universidad de California, Santa Cruz, en Crown College, un edificio de dormitorios lleva su nombre,
• El Gauss Haus, un Centro de RMN en el Universidad de Utah,
• El-Friedrich-Carl Gauss Escuela de Matemáticas, Informática, Administración de Empresas, Economía y Ciencias Sociales de Universidad de Braunschweig,
• El edificio de Gauss - Universidad de Idaho (Facultad de Ingeniería).

En 1929, el polaco matemático Marian Rejewski, que resolvería el alemán máquina de cifrado Enigma en diciembre de 1932, comenzó a estudiar estadísticas actuariales en Göttingen. A petición de su Profesor de la Universidad de Poznan, Zdzisław Krygowski, al llegar a Göttingen Rejewski depositó flores en la tumba de Gauss.

Escritos

• 1799: Tesis doctoral sobre la Teorema fundamental del álgebra, con el título: Demonstratio nova theorematis omnem functionem algebraicam rationalem Integram unius variabilis en factors reales primi vel secundi posse resolvi Gradus ("Nueva demostración del teorema de que cada función algebraica integral de una variable se puede descomponer en factores reales ( es decir, los polinomios) del primer o segundo grado ")
• 1801: Disquisitiones Arithmeticae. Traducción alemana de H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae y otros documentos sobre la teoría de números) (Segunda edición). Nueva York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 1-453. Traducción Inglés por Arthur A. Clarke Disquisitiones Arithemeticae (Segunda edición, corregida). Nueva York: Springer. 1986. ISBN 0-387-96254-9.
• 1808: Theorematis arithmetici demonstratio nova. Göttingen: Comentario. Soc. regiae sci, Göttingen XVI. Traducción alemana de H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae y otros documentos sobre la teoría de números) (Segunda edición). Nueva York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 457-462 [presenta Lema de Gauss, lo usa en la tercera prueba de la reciprocidad cuadrática]
• 1809: Theoria Motus Corporum Coelestium en sectionibus conicis Solem ambientium (Theorie der Bewegung der Himmelskörper, die die Sonne en Kegelschnitten umkreisen), traducción de Inglés por CH Davis, reimpreso 1963, Dover, Nueva York.
• 1811: Summatio serierun quarundam singularium. Göttingen: Comentario. Soc. regiae sci, Göttingen. Traducción alemana de H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae y otros documentos sobre la teoría de números) (Segunda edición). Nueva York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 463-495 [Determinación de la señal de la cuadrática suma de Gauss, lo utiliza para dar la cuarta prueba de la reciprocidad cuadrática]
• 1812: Disquisitiones Circa Generales serieM Infinitam
• 1818: Theorematis fundamentallis en doctrina de residuis quadraticis demonstrationes et amplicationes novas. Göttingen: Comentario. Soc. regiae sci, Göttingen. Traducción alemana de H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae y otros documentos sobre la teoría de números) (Segunda edición). Nueva York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 496-510 [Quinta y sexta pruebas de reciprocidad cuadrática]
• 1821, 1823 y 1826: Theoria combinationis observationum erroribus minimis obnoxiae. Drei Abhandlungen betreffend Muere el als Wahrscheinlichkeitsrechnung Grundlage des Gauß'schen Fehlerfortpflanzungsgesetzes. (Tres ensayos sobre el cálculo de las probabilidades como la base de la ley de Gauss de la propagación de errores) Traducción Inglés por GW Stewart, 1987, Sociedad de Matemática Industrial.
• 1827: Disquisitiones circa superficies curvas Generales, Commentationes societatis regiae Scientiarum Gottingesis recentiores. Volumen VI, pp. 99-146. " Investigaciones Generales de superficies curvas "(publicado 1965) Raven Press, Nueva York, traducido por AMHiltebeitel y JCMorehead.
• 1828: Theoria biquadraticorum residuorum, Commentatio prima. Göttingen: Comentario. Soc. regiae sci, Göttingen 6. Traducción alemán por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae y otros documentos sobre la teoría de números) (Segunda edición). Nueva York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 511-533 [hechos elementales sobre residuos bicuadráticos, prueba uno de los suplementos de la ley de reciprocidad biquadratic (el carácter de biquadratic 2)]
• 1832: Theoria biquadraticorum residuorum, Commentatio secunda. Göttingen: Comentario. Soc. regiae sci, Göttingen 7. Traducción alemán por H. Maser Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae y otros documentos sobre la teoría de números) (Segunda edición). Nueva York: Chelsea. 1965. ISBN 0-8284-0191-8, pp. 534-586 [presenta el Enteros de Gauss, estados (sin pruebas) la ley de reciprocidad bicuadrático, prueba la ley complementaria: Para 1 + i]
• 1843-1844: Über Untersuchungen Gegenstände der höheren Geodäsie. Erste Abhandlung, Abhandlungen der Gesellschaft der Königlichen Wissenschaften en Göttingen. Zweiter Band, pp. 3-46
• 1846-1847: Über Untersuchungen Gegenstände der höheren Geodäsie. Zweite Abhandlung, Abhandlungen der Gesellschaft der Königlichen Wissenschaften en Göttingen. Dritter Band, pp. 3-44
• Mathematisches Tagebuch 1796-1814, Ostwaldts Klassiker, Harri Deutsch Verlag 2005, mit Anmerkungen von Neumamn, ISBN 978-3-8171-3402-1 (Traducción Inglés con anotaciones de Jeremy Gray:. Expositiones Matemáticas 1984)
• Obras colectivas de Gauss son gratis Esto incluye traducciones al alemán de textos latinos y comentarios de diversas autoridades