Teoría del caos

Una parcela de la Lorenz atractor para los valores r = 28, σ = 10, b = 8/3

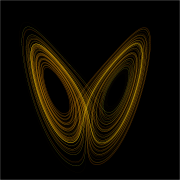
En las matemáticas y la física , la teoría del caos se describe el comportamiento de ciertos no lineal sistemas dinámicos que pueden presentar dinámicas que son altamente sensibles a las condiciones iniciales (denominados popularmente como el efecto mariposa). Como resultado de esta sensibilidad, que se manifiesta como un crecimiento exponencial de las perturbaciones en las condiciones iniciales, el comportamiento de los sistemas caóticos parece ser azar. Esto sucede a pesar de que estos sistemas son determinista, lo que significa que la dinámica de sus futuros están totalmente definidas por sus condiciones iniciales, sin elementos aleatorios involucrados. Este comportamiento se conoce como el caos determinista, o simplemente caos.

Visión de conjunto

Comportamiento caótico se ha observado en el laboratorio en una variedad de sistemas, incluyendo circuitos eléctricos, láseres , oscilantes reacciones químicas , dinámica de fluidos, y dispositivos mecánicos y magneto-mecánicas. Las observaciones de comportamiento caótico en la naturaleza incluyen la dinámica de los satélites en el sistema solar , la evolución temporal de la el campo magnético de los cuerpos celestes, crecimiento de la población en la ecología , la dinámica de los potenciales de acción en las neuronas, y vibraciones moleculares. Ejemplos cotidianos de los sistemas caóticos incluyen tiempo y el clima . Existe cierta controversia sobre la existencia de una dinámica caótica en las placas tectónicas y en la economía .

Los sistemas que exhiben caos matemático son deterministas y así ordenada en algún sentido; este uso técnico de la palabra caos está en desacuerdo con el lenguaje común, lo que sugiere un completo desorden. Un campo relacionado de la física llamada sistemas cuánticos estudios teoría del caos que siguen las leyes de la mecánica cuántica . Recientemente, otro campo, llamado caos relativista, ha surgido para describir sistemas que siguen las leyes de la relatividad general .

Además de ser ordenada en el sentido de ser determinista, los sistemas caóticos tienen generalmente bien definidos estadísticas . Por ejemplo, el Sistema de Lorenz en la foto es caótica, pero tiene una estructura claramente definida. Caos acotada es un término útil para describir modelos de trastorno.

Historia

Fractal helecho creado usando caos juego. Las formas naturales (helechos, nubes, montañas, etc.) pueden ser recreados a través de un Sistema iterativo de funciones (IFS).

El primer descubridor del caos plausiblemente puede argumentar que ser Jacques Hadamard, quien en 1898 publicó un influyente estudio del movimiento caótico de una partícula libre se desliza sin fricción sobre una superficie de curvatura negativa constante. En el sistema estudiado, Billar de Hadamard, Hadamard fue capaz de demostrar que todas las trayectorias son inestables, en que todas las trayectorias de las partículas divergen de manera exponencial el uno del otro, con un positivo Exponente de Lyapunov.

A principios de la década de 1900 Henri Poincaré, mientras que el estudio de la problema de tres cuerpos, encontraron que no puede haber órbitas que son no periódica, y sin embargo no siempre aumenta ni acercarse a un punto fijo. Gran parte de la primera teoría se desarrolló casi en su totalidad por los matemáticos, con el nombre de teoría ergódica. Estudios posteriores, también en el tema de ecuaciones diferenciales no lineales, se llevaron a cabo por GD Birkhoff, AN Kolmogorov, ML Cartwright, JE Littlewood, y Stephen Smale. A excepción de Smale, estos estudios fueron inspirados directamente por la física: el problema de los tres cuerpos en el caso de Birkhoff, la turbulencia y problemas astronómicos en el caso de Kolmogorov, y la ingeniería de radio en el caso de Cartwright y Littlewood. Aunque no se había observado el movimiento planetario caótico, los experimentadores habían encontrado turbulencia en el movimiento del fluido y la oscilación no periódica en los circuitos de radio sin el beneficio de una teoría para explicar lo que estaban viendo.

A pesar de ideas iniciales en la primera mitad del siglo, la teoría del caos se formalizó como tal sólo después de mediados de siglo, cuando se hizo evidente por primera vez para algunos científicos que teoría lineal, la teoría del sistema imperante en ese momento, simplemente no podía explicar el comportamiento observado de ciertos experimentos como el de la mapa logístico. Lo que había sido previamente excluidos como medir la imprecisión y simple " ruido "fue considerado por las teorías del caos como un componente completo de los sistemas estudiados.

El principal catalizador para el desarrollo de la teoría del caos fue la electrónica equipo . Gran parte de las matemáticas de la teoría del caos implica la iteración repetida de fórmulas matemáticas simples, lo que sería poco práctico hacerlo a mano. Ordenadores electrónicos hacen estos cálculos repetidos práctico, mientras que las cifras y las imágenes han permitido visualizar estos sistemas. Uno de los primeros ordenadores electrónicos digitales, ENIAC, se utiliza para ejecutar los modelos de predicción meteorológica simples.

La turbulencia en el torbellino de punta de un ala de avión. Los estudios de la punto crítico más allá del cual un sistema crea turbulencia era importante para la teoría del caos, analiza, por ejemplo, por el físico soviético Lev Landau que desarrolló el Teoría de Landau-Hopf de turbulencia. David Ruelle y Floris Takens más tarde predijo, en contra de Landau, que turbulencia del fluido podría desarrollar a través de una atractor extraño, un concepto central de la teoría del caos.

Uno de los pioneros de la teoría era Edward Lorenz cuyo interés en el caos se produjo accidentalmente a través de su trabajo en la predicción del tiempo en 1961 . Lorenz estaba usando un sencillo digital de la computadora , un Royal McBee LGP-30, para ejecutar su simulación meteorológica. Quería ver una secuencia de datos de nuevo y para ahorrar tiempo comenzó la simulación en el medio de su curso. Él fue capaz de hacer esto al introducir una copia impresa de los datos correspondientes a las condiciones en el medio de su simulación que había calculado la última vez.

Para su sorpresa, el tiempo que la máquina comenzó a predecir era completamente diferente del tiempo calculado antes. Lorenz rastreado esto a la impresión de la computadora. El equipo trabajó con una precisión de 6 dígitos, pero la impresión redondea las variables fuera a un número de 3 dígitos, por lo que un valor como 0.506127 fue impreso como 0,506. Esta diferencia es muy pequeña y el consenso en el momento habría sido que debería haber tenido prácticamente ningún efecto. Sin embargo Lorenz había descubierto que los pequeños cambios en las condiciones iniciales producen grandes cambios en el resultado a largo plazo. El descubrimiento de Lorenz, que dio su nombre a Atractores de Lorenz, demostraron que la meteorología no podía predecir razonablemente el tiempo más allá de un período semanal (como máximo).

El año anterior, Benoit Mandelbrot encontró patrones recurrentes en todas las escalas de datos sobre los precios del algodón. Antes, había estudiado teoría de la información y concluyó ruido fue modelado como una Conjunto de Cantor: períodos en cualquier escala, la proporción de los períodos que contiene ruido libre de errores era un constant-- tanto errores eran inevitables y deben ser planificadas para la incorporación redundancia. Mandelbrot describe tanto el Efecto Noé (en el que pueden ocurrir repentinos cambios discontinuos, por ejemplo, en los precios de una acción después de una mala noticia, por lo tanto difícil de distribución normal teoría en las estadísticas , también conocido como la curva de Bell) y el Joseph efecto (en la que la persistencia de un valor puede ocurrir durante un tiempo, sin embargo, cambia de repente después). En 1967, publicó ¿Qué longitud tiene la costa de Gran Bretaña? Estadística auto-similaridad y fraccional dimensión, lo que demuestra que la longitud de una línea costera varía con la escala del instrumento de medición, se parece a sí mismo a todas las escalas, y es infinita en longitud para un dispositivo de medición infinitamente pequeño. Argumentando que aparece una bola de hilo sea de 1 dimensión (ahora), en 3 dimensiones (bastante cerca), o 1-dimensional (cerrar), argumentó que las dimensiones de un objeto son en relación con el observador y pueden ser fraccionada. Un objeto cuya irregularidad es constante en diferentes escalas ("auto-similitud") es un fractal (por ejemplo, la Curva de Koch o " copo de nieve ", que es infinitamente larga todavía encierra un espacio finito con dimensiones = 1,2618; o la Menger esponja y la Junta de Sierpinski). En 1975 publicó Mandelbrot La geometría fractal de la naturaleza, que se convirtió en un clásico de la teoría del caos. Los sistemas biológicos, tales como la ramificación de los sistemas circulatorio y bronquiales probaron para ajustar un modelo fractal.

Yoshisuke Ueda identificado independientemente un fenómeno caótico como tal por el uso de un computadora analógica el 27 de noviembre de 1961. El caos exhibido por una computadora analógica es un fenómeno real, en contraste con aquellos que las computadoras digitales calculan, que tiene un tipo diferente de límite de precisión. Profesor supervisor de Ueda, Hayashi, no creía en el caos, y por lo tanto se prohíbe Ueda publicar sus hallazgos hasta 1970 .

En diciembre de 1977 el Academia de Ciencias de Nueva York organizó el primer simposio sobre el caos, a la que asistieron David Ruelle, Robert May, James Yorke (quien acuñó el término "caos" como se usa en las matemáticas), Robert Shaw (un físico, parte de la Grupo Eudaemons con J. Doyne Farmer y Norman Packard que intentó encontrar un método matemático para vencer ruleta y, luego creó con ellos el Colectivo Sistemas Dinámicos en Santa Cruz), y el meteorólogo Edward Lorenz.

El año siguiente, Mitchell Feigenbaum publicó el artículo señalado "Quantitative Universalidad para una clase de Transformaciones no lineales", donde describió mapas logísticos. Feigenbaum había aplicado la geometría fractal para el estudio de las formas naturales, tales como líneas de costa. Feigenbaum notablemente descubrió la universalidad en el caos, lo que permite una aplicación de la teoría del caos a muchos fenómenos diferentes.

En 1979, Albert J. Libchaber, durante un simposio organizado en Aspen por Pierre Hohenberg, presentó su observación experimental de la cascada de bifurcación que conduce al caos y la turbulencia en convectivo Sistemas de Rayleigh-Benard. Fue galardonado con el Premio Wolf en Física en 1986 junto con Mitchell J. Feigenbaum "por su demostración brillante experimental de la transición a la turbulencia y el caos en los sistemas dinámicos".

La Academia de Ciencias de Nueva York y luego co-organizada, en 1986, con la Instituto Nacional de Salud Mental y la Oficina de Investigación Naval de la primera conferencia importante sobre el caos en la biología y la medicina. Bernardo Huberman presenta de esta manera un modelo matemático de la trastorno de seguimiento de los ojos de los esquizofrénicos . La teoría del caos posteriormente renovado la fisiología en la década de 1980, por ejemplo, en el estudio de la patológica ciclos cardíacos.

En 1987, Per Bak, Chao Tang y Kurt Wiesenfeld publicó un artículo en Cartas Physical Review describen por primera vez criticidad auto-organizada (SOC), considerado como uno de los mecanismos por los cuales complejidad surge en la naturaleza. Junto enfoques en gran parte de laboratorio basado, como el Bak-Tang-Wiesenfeld pila de arena, muchas otras investigaciones se han centrado en los sistemas naturales o sociales a gran escala que se sabe (o sospecha) para mostrar escala invariante comportamiento. Si bien estos métodos no siempre fueron bienvenidos (al menos inicialmente) por especialistas en los temas que se estudian, SOC ha, sin embargo, llegar a establecerse como un fuerte candidato para explicar una serie de fenómenos naturales, como: terremotos (que, mucho antes de SOC fue descubierto, eran conocidos como una fuente de comportamiento invariante en escala como el La ley de Gutenberg-Richter que describe la distribución estadística de los tamaños del terremoto, y la Ley Omori describir la frecuencia de réplicas); erupciones solares; fluctuaciones en los sistemas económicos como los mercados financieros (referencias a SOC son comunes en econofísica); formación del paisaje; incendio forestal; deslizamientos de tierra; epidemias; y la evolución biológica (donde SOC se ha invocado, por ejemplo, como el mecanismo dinámico detrás de la teoría del "equilibrio puntuado" propuesto por Niles Eldredge y Stephen Jay Gould ). Preocupante, dadas las implicaciones de una la distribución libre de escala de tamaños de eventos, algunos investigadores han sugerido que otro fenómeno que debe ser considerado un ejemplo de SOC es la ocurrencia de guerras . Estas investigaciones "aplicación" del SOC han incluido dos intentos de modelado (ya sea en desarrollo de nuevos modelos o adaptar las existentes a las características específicas de un sistema natural dado), y el análisis de datos extensos para determinar la existencia y / o características de leyes de escala naturales.

El mismo año, James Gleick publicó Caos: la creación de una ciencia, que se convirtió en un best-seller y presentó los principios generales de la teoría del caos, así como su historia para el público en general. Al principio, los ámbitos de trabajo de unos pocos individuos, aislados, la teoría del caos surgió progresivamente como transdisciplinar y disciplina institucional, principalmente bajo el nombre de análisis de sistemas no lineales. Aludiendo a Thomas Kuhn concepto de una 's cambio de paradigma expuesto en La estructura de las revoluciones científicas (1962), muchos "chaologists" (como un poco de auto-nominado a sí mismos) afirmó que esta nueva teoría fue un ejemplo de como el cambio, la tesis sostenida por J. Gleick.

La disponibilidad de ordenadores más potentes, más baratos amplía la aplicabilidad de la teoría del caos. En la actualidad, la teoría del caos sigue siendo un área de investigación muy activa, que implica muchos diferentes disciplinas (matemáticas, la topología , la física, la biología de las poblaciones, la biología, la meteorología, la astrofísica, teoría de la información, etc.).

Dinámica caótica

Para un sistema dinámico para ser clasificado como caótica, debe tener las siguientes propiedades:

• que debe ser sensible a las condiciones iniciales,
• tendria que ser mezcla topológicamente, y
• su órbitas periódicas deben ser densa.

La sensibilidad a las condiciones iniciales significa que cada punto en un sistema de este tipo está arbitrariamente estrechamente aproximada por otros puntos con significativamente diferentes trayectorias futuras. Así, un arbitrariamente pequeña perturbación de la trayectoria actual puede conducir a significativamente diferente comportamiento futuro.

La sensibilidad a las condiciones iniciales se conoce popularmente como la " efecto mariposa ", llamada así por el título de un trabajo presentado por Edward Lorenz en 1972 para la Asociación Americana para el Avance de la Ciencia en Washington, DC La previsibilidad titulado: ¿El aleteo de una mariposa en Brasil provocó un tornado en Texas El aleteo representa un pequeño cambio en la condición inicial del sistema, lo que provoca una cadena de? eventos que conducen a fenómenos a gran escala. Había la mariposa no batió sus alas, la trayectoria del sistema podría haber sido muy diferente.

La sensibilidad a las condiciones iniciales a menudo se confunde con el caos en los relatos populares. También puede ser una propiedad sutil, ya que depende de una selección de métrica, o la noción de distancia en el espacio de fases del sistema. Por ejemplo, considere el sistema dinámico sencillo producido por duplicar repetidamente un valor inicial (definida por la cartografía en la recta real de x a 2x). Este sistema tiene la dependencia sensible de las condiciones iniciales en todas partes, ya que cualquier par de puntos cercanos eventualmente se convertirá en muy distantes entre sí. Sin embargo, tiene un comportamiento extremadamente simple, ya que todos los puntos excepto 0 tienden a infinito. Si en cambio usamos la métrica acotada en la línea obtenida sumando el punto en el infinito y ver el resultado en forma de círculo, el sistema ya no es sensible a las condiciones iniciales. Por esta razón, en la definición de caos, la atención se limitan normalmente a los sistemas con métricas acotadas, o cerrado, acotado subgrupos invariantes de sistemas no acotados.

Incluso para sistemas acotados, la sensibilidad a las condiciones iniciales no es idéntico con el caos. Por ejemplo, considere el toro de dos dimensiones descritas por un par de ángulos (x, y), cada uno que oscila entre cero y 2π. Definir un mapeo que se lleva a cualquier punto (x, y) a (2x, y + a), donde a es cualquier número tal que un / 2π es irracional. Debido a la duplicación de la primera coordenada, el mapeo exhibe dependencia sensible de las condiciones iniciales. Sin embargo, debido a la rotación irracional en la segunda coordenada, no hay órbitas periódicas, y por lo tanto la asignación no es caótica de acuerdo con la definición anterior.

Mezcla Topológicamente significa que el sistema evolucionará con el tiempo de manera que cualquier región o conjunto abierto de su espacio de fase, finalmente se solapará con cualquier otra región. Aquí, "la mezcla" sirve realmente para corresponder a la intuición estándar: la mezcla de color colorantes o fluidos es un ejemplo de un sistema caótico.

Attractors

Algunos sistemas dinámicos son caóticos en todas partes (véase, por ejemplo Difeomorfismos Anosov), pero en muchos casos el comportamiento caótico se encuentra solamente en un subconjunto del espacio de fase. Los casos de mayor interés surgen cuando el comportamiento caótico se lleva a cabo en un atractor, desde entonces, un gran conjunto de condiciones iniciales dará lugar a órbitas que confluyen a esta región caótica.

Una manera fácil de visualizar un atractor caótico es comenzar con un punto en el cuenca de atracción del atractor, y luego simplemente trazar su órbita posterior. Debido a la condición de transitividad topológica, es probable que para producir una imagen de todo el atractor final.

Diagrama de fases para un amortiguado impulsado péndulo, con doble periodo de movimiento

Por ejemplo, en un sistema que describe un péndulo, el espacio de fases podría ser de dos dimensiones, que consiste en información acerca de la posición y velocidad. Se podría trazar la posición de un péndulo contra su velocidad. Un péndulo en reposo se representa como un punto, y una en movimiento periódico se representará gráficamente como una curva cerrada simple. Cuando una parcela tal forma una curva cerrada, la curva se denomina órbita. Nuestra péndulo tiene un número infinito de tales órbitas, formando una lápiz de elipses anidados sobre el origen.

Los atractores extraños

Si bien la mayoría de los tipos de movimiento mencionadas anteriormente dan lugar a atractores muy simples, tales como puntos y curvas de círculo como llamadas ciclos límite, movimiento caótico da lugar a lo que se conoce como atractores extraños, atractores que pueden tener gran detalle y complejidad. Por ejemplo, un modelo tridimensional simple del Sistema meteorológico Lorenz da lugar a la famosa Atractor de Lorenz. El atractor de Lorenz es quizás uno de los diagramas del sistema caóticos más conocidos, probablemente porque no sólo fue uno de los primeros, pero es uno de los más complejos y, como tal, da lugar a un patrón muy interesante que se parece a las alas de una mariposa. Otra de tales atractor es el Mapa Rössler, que experimenta período de dos ruta duplicación al caos, al igual que el mapa logístico.

Los atractores extraños ocurren en ambos sistemas dinámicos continuos (tales como el sistema de Lorenz) y en algunas sistemas discretos (tales como la Hénon mapa). Otros sistemas dinámicos discretos tienen una estructura repelente llama Julia establece que se forma en el límite entre las cuencas de atracción de puntos fijos - conjuntos de Julia puede pensarse repelentes como extraños. Ambos atractores extraños y conjuntos de Julia tienen típicamente un fractal estructura.

La Poincaré-Bendixson teorema muestra que un atractor extraño sólo puede surgir en un sistema dinámico continuo si tiene tres o más dimensiones. Sin embargo, no hay tal restricción se aplica a sistemas discretos, que pueden exhibir atractores extraños en dos o incluso uno sistemas dimensionales.

Las condiciones iniciales de tres o más cuerpos que interactúan a través de la atracción gravitatoria (ver el n problema -cuerpo) puede estar dispuesto para producir un movimiento caótico.

Complejidad mínima de un sistema caótico

Diagrama de bifurcación de un mapa logístico, mostrando un comportamiento caótico pasado un umbral

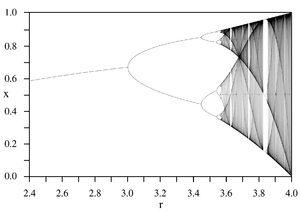
Los sistemas simples también pueden producir caos sin depender de ecuaciones diferenciales . Un ejemplo es el mapa logístico, que es una ecuación de diferencia ( relación de recurrencia) que describe el crecimiento de la población a través del tiempo.

Incluso la evolución de los sistemas discretos simples, tales como autómatas celulares, en gran medida puede depender de las condiciones iniciales. Stephen Wolfram ha investigado un autómata celular con esta propiedad, denominado por él regla 30.

Un modelo mínimo de conservador (reversible) comportamiento caótico es proporcionada por Mapa gato de Arnold.

La teoría matemática

Teorema de Sarkovskii es la base de la Li y Yorke (1975) prueba de que cualquier sistema unidimensional que exhibe un ciclo periódico de período de tres también se mostrará ciclos regulares de cada otra longitud, así como órbitas completamente caóticos.

Los matemáticos han ideado muchas maneras de hacer declaraciones cuantitativas sobre los sistemas caóticos. Éstas incluyen: dimensión fractal del atractor, Exponentes de Lyapunov, parcelas de recurrencia, Mapas de Poincaré, diagramas de bifurcación, y operador de transferencia.

Distinguir azar de datos caótica

Puede ser difícil saber a partir de los datos si un proceso observado física u otro es aleatoria o caótica, porque en la práctica no existen series temporales consiste en pura 'señal'. Siempre habrá algún tipo de ruido corruptora, incluso si está presente como salida redonda o error de truncamiento. Así, cualquier serie de tiempo real, incluso si la mayoría determinista, contendrá algo de aleatoriedad.

Todos los métodos para distinguir los procesos deterministas y estocásticos se basan en el hecho de que un sistema determinista siempre evoluciona de la misma manera a partir de un determinado punto de partida. Así, dada una serie de tiempo para probar el determinismo, se puede:

1. elegir un estado de prueba;
2. buscar en la serie temporal de un estado similar o 'cerca'; y
3. comparar sus respectivas evoluciones de tiempo.

Definir el error como la diferencia entre el tiempo de evolución de la situación 'test' y la evolución temporal del estado cerca. Un sistema determinista tendrá un error que, o bien sigue siendo pequeño (solución estable, regular) o aumenta exponencialmente con el tiempo (caos). Un sistema estocástico tendrá un error distribuida al azar.

Esencialmente todas las medidas de determinismo tomadas de series de tiempo se basan en la búsqueda de los estados más cercanos a un estado de "prueba" dado (es decir, la dimensión de correlación, exponentes de Liapunov, etc.). Para definir el estado de un sistema uno se basa típicamente en métodos de incrustación de espacio de fase. Normalmente uno elige una dimensión de inmersión, e investiga la propagación del error entre dos estados vecinos. Si el error parece aleatoria, se aumenta la dimensión. Si usted puede aumentar la dimensión de obtener un error de mirar determinista, entonces ya está. Aunque puede sonar simple en realidad no es. Una complicación es que a medida que aumenta la dimensión de la búsqueda de un estado cercano requiere mucho más tiempo de cálculo y una gran cantidad de datos (la cantidad de datos necesarios aumenta exponencialmente con la dimensión de inmersión) para encontrar un lugar próximo candidato. Si la dimensión de inmersión (número de medidas por estado) se elige demasiado pequeño (menor que el "verdadero" valor) de datos deterministas pueden parecen ser al azar, pero en teoría no hay ningún problema de elegir la dimensión demasiado grande - el método funcionará. En la práctica, algo que se aproxime a unos 10 dimensiones se considera tan grande que una descripción estocástica es probablemente más adecuada y conveniente de todos modos.

Aplicaciones

La teoría del caos se aplica en muchas disciplinas científicas: la matemática , biología , ciencias de la computación , economía , ingeniería , finanzas , filosofía , física , política , dinámica de la población, la psicología , y robótica.

La teoría del caos también se está aplicando actualmente a los estudios médicos de epilepsia , específicamente a la predicción de ataques aparentemente al azar mediante la observación de las condiciones iniciales.

Literatura

Artículos

• Li, TY y Yorke, JA "Período de Tres Implica Caos." American Mathematical Monthly 82, 985-992, 1975.
• Kolyada, SF "Sensibilidad de Li-Yorke y otros conceptos de caos", Matemáticas ucraniano. J. 56 (2004), desde 1242 hasta -1257.
• CE Shannon, " Una teoría matemática de la comunicación ", Campana System Technical Journal, vol. 27, pp. 379-423, 623-656, julio, octubre, 1948

Los libros de texto

• Alligood, KT (1997) Chaos:. Una introducción a los sistemas dinámicos. Springer-Verlag New York, LLC. ISBN 0-387-94677-2.
• Baker, GL (1996). El caos, la dispersión y la Mecánica Estadística. Cambridge University Press. ISBN 0-521-39511-9.
• Badii, R .; A. Politi (1997). "Complejidad: estructuras jerárquicas y la ampliación de la física". Cambridge University Press. ISBN 0521663857. http://www.cambridge.org/catalogue/catalogue.asp?isbn=0521663857.
• Devaney, Robert L. (2003). Una introducción a Chaotic Sistemas Dinámicos, 2ª ed,. Westview Press. ISBN 0-8133-4085-3.
• Gollub, JP; Baker, GL (1996). Dinámica caótica. Cambridge University Press. ISBN 0-521-47685-2.
• Gutzwiller, Martin (1990). El caos en la mecánica clásica y cuántica. Springer-Verlag New York, LLC. ISBN 0-387-97173-4.
• Hoover, William Graham (1999,2001). Tiempo de reversibilidad, Simulación Computacional, y el Caos. Científico Mundial. ISBN 981-02-4073-2.
• Kiel, L. Douglas; Elliott, Euel W. (1997). Teoría del Caos en las Ciencias Sociales. Perseo Publishing. ISBN 0-472-08472-0.
• Luna, Francisco (1990). Chaotic y Fractal Dynamics. Springer-Verlag New York, LLC. ISBN 0-471-54571-6.
• Ott, Edward (2002). Caos en Sistemas Dinámicos. Cambridge University Press Nueva, York. ISBN 0-521-01084-5.
• Strogatz, Steven (2000). Dinámica no lineal y caos. Perseo Publishing. ISBN 0-7382-0453-6.
• Sprott, Julien Clinton (2003). El caos y el análisis de series temporales. Oxford University Press. ISBN 0-19-850840-9.
• Tél, Tamás; Gruiz, Márton (2006) la dinámica caótica:. Una introducción sobre la base de la mecánica clásica. Cambridge University Press. ISBN 0-521-83912-2.
• Tufillaro, Abbott, Reilly (1992). Una aproximación experimental a la dinámica no lineal y caos. Addison-Wesley Nueva York. ISBN 0-201-55441-0.
• Zaslavsky, George M. (2005). Hamiltoniano Caos y fraccionarios Dynamics. Oxford University Press. ISBN 0-198-52604-0.

Obras semitécnico y populares

• Ralph H. Abraham y Yoshisuke Ueda (Ed.), El Caos Avant-Garde: Memorias de los primeros días de la teoría del caos, World Scientific Publishing Company, 2001, 232 pp.
• Michael Barnsley, fractales todas partes, Academic Press 1988, 394 pp.
• Richard J Bird, Caos y de la Vida: La complejidad y orden de la Evolución y Pensamiento, Columbia University Press 2003, 352 pp.
• John Briggs y David Peat, turbulento Espejo:: Una guía ilustrada de la teoría del caos y la Ciencia de la Totalidad, Harper Perenne 1990, 224 pp.
• John Briggs y David Peat, Siete Lecciones de la vida del Caos: la sabiduría espiritual de la ciencia del cambio, Harper Perenne 2000, 224 pp.
• Lawrence A. Cunningham, de Random Walks a Chaotic Crashes: El Linear Genealogía del mercado de capitales eficiente Hipótesis, George Washington Law Review, vol. 62, 1994, 546 pp.
• Leon Glass y Michael C. Mackey, desde relojes a Chaos: El ritmo de la vida, Princeton University Press 1988, 272 pp.
• James Gleick, Caos: la creación de una ciencia, Nueva York: Penguin, 1988. 368 pp.
• John Gribbin, Profundo Sencillez,
• L Douglas Kiel, Euel W Elliott (ed.), La teoría del caos en las ciencias sociales: fundamentos y aplicaciones de la Universidad de Michigan Press, 1997, 360 pp.
• Arvind Kumar, Caos, fractales y la auto-organización; Nuevas perspectivas sobre la complejidad de la naturaleza, National Book Trust, 2003.
• Hans Lauwerier, Fractales, Princeton University Press, 1991.
• Edward Lorenz, La esencia del caos, de la Universidad de Washington Press, 1996.
• Heinz-Otto Peitgen y Dietmar Saupe (Eds.), La Ciencia de Imágenes Fractal, Springer 1988, 312 pp.
• Clifford A. Pickover, Informática, Diseño, Caos, y belleza: Gráficos de un mundo invisible, St Martins Pr 1991.
• Ilya Prigogine e Isabelle Stengers, orden en el caos, Bantam 1984.
• H.-O. Peitgen y PH Richter, la belleza de los fractales: Imágenes de Complejo Sistemas Dinámicos, Springer 1986, 211 pp.
• David Ruelle, Chance y el Caos, Princeton University Press 1993.
• David Ruelle, Chaotic Evolución y atractores extraños, Cambridge University Press, 1989.
• Peter Smith, Explicar Caos, Cambridge University Press, 1998.
• Ian Stewart, ¿Dios juega a los dados ?: Las Matemáticas del Caos, Blackwell Publishers, 1990.
• Steven Strogatz, Sync: La ciencia emergente del orden espontáneo, Hiperión, 2003.
• Yoshisuke Ueda, El camino a Caos, Pr aérea, 1993.
• M. Mitchell Waldrop, Complejidad: La Ciencia Emergente en el borde de la Orden y el Caos, Simon & Schuster, 1992.