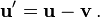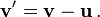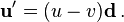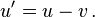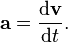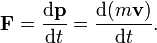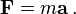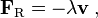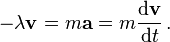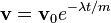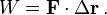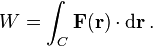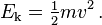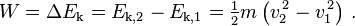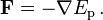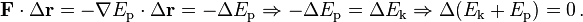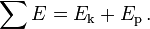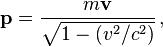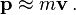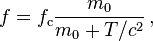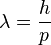La mecánica clásica
Antecedentes
SOS cree que la educación da una mejor oportunidad en la vida para los niños en el mundo en desarrollo también. Haga clic aquí para obtener más información sobre SOS Children.
| La mecánica clásica |
|---|
|
Ramas
|
Formulaciones
|
Conceptos fundamentales
|
Temas básicos
|
El movimiento de rotación
|
En la física , la mecánica clásica es una de las dos principales sub-campos de la la mecánica, que tiene que ver con el conjunto de leyes físicas que describen el movimiento de cuerpos bajo la acción de un sistema de fuerzas. El estudio del movimiento de los cuerpos es muy antigua, por lo que la mecánica clásica de uno de los temas más antiguos y más grandes de la ciencia , la ingeniería y la tecnología .
La mecánica clásica describe el movimiento de objetos macroscópicos, desde proyectiles a partes de maquinaria, así como objetos astronómicos, tales como vehículos espaciales, planetas , estrellas y galaxias . Además de esto, muchas especializaciones dentro del tema tratan con los gases , líquidos , sólidos y otros subtemas específicos. La mecánica clásica proporciona resultados muy precisos, siempre y cuando el dominio de estudio se limita a los objetos grandes y las velocidades involucradas no se acercan a la velocidad de la luz . Cuando los objetos se tratan convertido suficientemente pequeño, se hace necesario introducir el otro mayor sub-campo de la mecánica, la mecánica cuántica , que reconcilia las leyes macroscópicas de la física con la naturaleza atómica de la materia y se encarga de la la dualidad onda-partícula de átomos y moléculas . En el caso de altas velocidades objetos se acercan a la velocidad de la luz, la mecánica clásica se ve reforzada por la relatividad especial . La relatividad general unifica la relatividad especial con La ley de Newton de la gravitación universal, lo que permite a los físicos a manejar la gravitación a un nivel más profundo.
El término mecánica clásica fue acuñado en el siglo 20 para describir el sistema de la física iniciada por Isaac Newton y muchos contemporánea del siglo 17 filósofos de la naturaleza, basándose en las teorías astronómicas anteriores de Johannes Kepler , que a su vez se basa en las observaciones precisas de Tycho Brahe y los estudios de la terrestre movimiento de proyectiles de Galileo . Desde la construcción de estos aspectos de la física mucho antes de la aparición de la física cuántica y la relatividad, algunas fuentes excluyen de Einstein la teoría de la relatividad de esta categoría. Sin embargo, un número de fuentes modernas sí incluyen la mecánica relativista, que a su juicio representa la mecánica clásica en su forma más desarrollada y más preciso.
La etapa inicial en el desarrollo de la mecánica clásica se refiere a menudo como la mecánica de Newton, y se asocia con los conceptos empleados por físicos y los métodos matemáticos inventados por el propio Newton, en paralelo con Leibniz , y otros. Esto se describe con más detalle en las siguientes secciones. Más tarde, se desarrollaron métodos más abstractos y generales, que lleva a la reformulación de la mecánica clásica conocido como Mecánica lagrangiana y Mecánica hamiltoniana. Estos avances se hicieron en gran parte en los siglos 18 y 19, y se extienden sustancialmente más allá del trabajo de Newton, en particular mediante el uso de mecánica analítica. En última instancia, las matemáticas desarrolladas para estos eran fundamentales para la creación de la mecánica cuántica.
Historia
Algunos Filósofos griegos de la antigüedad, entre ellos Aristóteles , fundador de La física aristotélica, puede haber sido el primero en mantener la idea de que "todo sucede por una razón" y que los principios teóricos pueden ayudar en la comprensión de la naturaleza. Mientras que para un lector moderno, muchas de estas ideas conservados saldré como eminentemente razonable, hay una falta evidente de ambos matemática teoría y controlada experimentar, tal como la conocemos. Estos dos resultaron ser factores decisivos en la formación de la ciencia moderna, y que comenzaron con la mecánica clásica.
La "ciencia de pesos" medieval (es decir, la mecánica) debe gran parte de su importancia para el trabajo de Jordanus Nemorarius. En el Elementa ponderum súper demonstrationem, se introduce el concepto de "posicional gravedad "y el uso de componentes de fuerzas .
El primero publicado explicación causal de los movimientos de los planetas fue Johannes Kepler Astronomia nova publicó en 1609. Llegó a la conclusión, basada en Observaciones de Tycho Brahe de la órbita de Marte , que las órbitas eran elipses. Esta ruptura con pensamiento antiguo estaba ocurriendo alrededor del mismo tiempo que Galileo estaba proponiendo leyes matemáticas abstractas para el movimiento de los objetos. Él puede (o no) han realizado el famoso experimento de dejar caer dos bolas de cañón de diferentes pesos de la torre de Pisa , mostrando que ambos cayeron al piso al mismo tiempo. La realidad de este experimento se disputa, pero, más importante aún, él llevó a cabo experimentos cuantitativos por bolas rodando sobre una plano inclinado. Su teoría de movimiento acelerado deriva de los resultados de tales experimentos, y forma una piedra angular de la mecánica clásica.

Como fundamento de sus principios de la filosofía natural, Isaac Newton propuso tres leyes del movimiento : el ley de la inercia , la segunda ley de la aceleración (mencionado anteriormente), y la ley de acción y reacción; y de ahí sentado las bases de la mecánica clásica. Tanto las leyes segundo y tercero de Newton se les dio tratamiento científico y matemático adecuado en Newton Philosophiæ Naturalis Principia Mathematica, que los distingue de los anteriores intentos de explicar los fenómenos similares, que eran incompletas, incorrectas, o dado poca expresión matemática precisa. Newton también enunció los principios de conservación del momento y momento angular . En mecánica, Newton también fue el primero en proporcionar la primera formulación científica y matemática correcta de gravedad en La ley de Newton de la gravitación universal. La combinación de las leyes del movimiento y la gravitación de Newton proporciona la descripción más completa y precisa de la mecánica clásica. Demostró que estas leyes se aplican a los objetos cotidianos, así como a los objetos celestes. En particular, se obtiene una explicación teórica de las leyes de Kepler del movimiento de los planetas.
Newton previamente inventó el cálculo , de las matemáticas, y lo utilizó para realizar los cálculos matemáticos. Para aceptabilidad, su libro, el Principia , se formuló en su totalidad en términos de los métodos geométricos de larga data, que pronto fueron eclipsadas por su cálculo. Sin embargo, fue Leibniz quien desarrolló la notación del derivado y integral hoy preferido.

Newton, y la mayoría de sus contemporáneos, con la notable excepción de Huygens, trabajaron en el supuesto de que la mecánica clásica sería capaz de explicar todos los fenómenos, incluyendo la luz , en forma de la óptica geométrica. Incluso al descubrir la llamada Anillos de Newton (un interferencia de ondas fenómeno) su explicación se quedó con su propia la teoría corpuscular de la luz.
Después de Newton, la mecánica clásica se convirtió en un campo principal de estudio en matemáticas, así como la física. Después de Newton, varias reformulaciones permite progresivamente la búsqueda de soluciones a un número mucho mayor de problemas. La primera notable re-formulación fue en 1788 por Joseph Louis Lagrange . Mecánica lagrangiana fue a su vez re-formulados en 1833 por William Rowan Hamilton.
Algunas dificultades fueron descubiertos en el siglo 19 que sólo puede ser resuelto por la física más moderna. Algunas de estas dificultades relacionadas con la compatibilidad con la teoría electromagnética , y el famoso Experimento de Michelson-Morley. La resolución de estos problemas llevaron a la teoría especial de la relatividad , incluye a menudo en la mecánica clásica plazo.
Un segundo conjunto de dificultades que estaban relacionados con la termodinámica. Cuando se combina con la termodinámica , la mecánica clásica lleva a la Gibbs paradoja de la clásica mecánica estadística , en los que la entropía no es una cantidad bien definida. La radiación del cuerpo negro no se explica sin la introducción de cuantos. Como experimentos alcanzaron el nivel atómico, la mecánica clásica no pudo explicar, ni siquiera aproximadamente, cosas tan básicas como la los niveles de energía y tamaños de los átomos y la efecto fotoeléctrico. El esfuerzo en la solución de estos problemas condujo al desarrollo de la mecánica cuántica .
Desde finales del siglo 20, el lugar de la mecánica clásica en la física ha sido ya no el de una teoría independiente. En su lugar, la mecánica clásica se considera ahora una teoría aproximada a la mecánica cuántica más generales. El énfasis se ha desplazado a la comprensión de las fuerzas fundamentales de la naturaleza como en el modelo estándar y sus extensiones más modernas en un unificado teoría del todo. La mecánica clásica es una teoría para el estudio del movimiento de las partículas no-mecánica cuántica, de baja energía en campos gravitatorios débiles. En la mecánica clásica del siglo 21 se ha ampliado en el dominio complejo y la mecánica clásica complejos exhibe comportamientos muy similares a la mecánica cuántica.
Descripción de la teoría
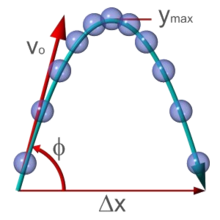
A continuación se presentan los conceptos básicos de la mecánica clásica. Para simplificar, a menudo modelos objetos del mundo real como partículas puntuales, los objetos con tamaño insignificante. El movimiento de una partícula punto se caracteriza por un pequeño número de parámetros: su posición, masa , y las fuerzas que se le aplican. Cada uno de estos parámetros se discute en turno.
En realidad, el tipo de objetos que la mecánica clásica puede describir siempre tienen un no-cero tamaño. (La física de partículas muy pequeñas, como el electrón , se describe con mayor precisión por la mecánica cuántica ). Los objetos con tamaño distinto de cero tienen un comportamiento más complicado que las partículas punto hipotético, debido a la adicional grados de libertad para ejemplo, un béisbol puede girar mientras se está moviendo. Sin embargo, los resultados para partículas puntuales se pueden utilizar para estudiar tales objetos tratándolos como objetos compuestos, compuestos por un gran número de partículas que interactúan de punto. El centro de masa de un objeto compuesto se comporta como una partícula puntual.
Usos mecánica clásica existen e interactúan nociones de sentido común de cómo la materia y las fuerzas. Se asume que la materia y la energía tienen atributos definidos, conocibles tales como que un objeto está en el espacio y su velocidad. También se supone que los objetos pueden estar directamente influidos sólo por su entorno inmediato, conocido como el principio de localidad. En la mecánica cuántica objetos pueden tener posición incognoscible o velocidad, o instantáneamente interactuar con otros objetos a distancia.
Posición y sus derivados
| La Derivadas SI "mecánica" (Es decir, no electromagnética o térmica) unidades con kg, m y s | |
| posición | m |
| posición angular / ángulo | sin unidades (radian) |
| velocidad | m · s -1 |
| velocidad angular | s -1 |
| aceleración | m · s -2 |
| aceleración angular | s -2 |
| tirón | m · s -3 |
| "Jerk angular" | s -3 |
| energía específica | m 2 · s -2 |
| tasa de dosis absorbida | m 2 · s -3 |
| momento de inercia | kg · m 2 |
| impulso | kg · m · s -1 |
| momento angular | kg · m 2 · s -1 |
| fuerza | kg · m · s -2 |
| esfuerzo de torsión | kg · m 2 · s -2 |
| energía | kg · m 2 · s -2 |
| energía | kg · m 2 · s -3 |
| presión y densidad de energía | kg · m -1 · s -2 |
| tensión superficial | kg · s -2 |
| constante de resorte | kg · s -2 |
| irradiancia y flujo de energía | kg · s -3 |
| viscosidad cinemática | m 2 · s -1 |
| viscosidad dinámica | kg · m -1 · s -1 |
| la densidad (densidad de masa) | kg · m -3 |
| la densidad (densidad peso) | kg · m-2 · s -2 |
| densidad numérica | m -3 |
| acción | kg · m 2 · s -1 |
La posición de una punto de partícula se define con respecto a un punto de referencia fijo arbitrario, O, en espacio, por lo general acompañado por un sistema de coordenadas, con el punto de referencia situado en el origen del sistema de coordenadas. Se define como el vector r de O a la partícula. En general, la partícula punto no necesita ser estacionaria con respecto a O, por lo que r es una función de t, el tiempo transcurrido desde un tiempo inicial arbitrario. En pre-Einstein de la relatividad (conocido como La relatividad de Galileo), el tiempo se considera un absoluto, es decir, el intervalo de tiempo entre cualquier par dado de eventos es la misma para todos los observadores. Además de confiar en tiempo absoluto, la mecánica clásica asume la geometría euclidiana para la estructura del espacio.
La velocidad y la velocidad
La velocidad , o la velocidad de cambio de la posición con el tiempo, se define como la derivada de la posición con respecto al tiempo o
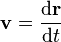 .
.
En la mecánica clásica, las velocidades son directamente aditivo y sustractivo. Por ejemplo, si un automóvil que viaja hacia el este a 60 kmh pasa otro coche en dirección este a 50 km / h, a continuación, desde la perspectiva del coche más lento, el coche más rápido se desplaza hacia el este a 60-50 = 10 km / h. Considerando que, desde la perspectiva del coche más rápido, el coche más lento se mueve 10 kmh al oeste. Las velocidades son directamente aditivo según magnitudes vectoriales; deben ser tratadas con el uso de análisis vectorial .
Matemáticamente, si la velocidad del primer objeto en la discusión anterior se denota por el vector u = u d y la velocidad de la segunda objeto por el vector v = v e, donde u es la velocidad de la primera objeto, v es la velocidad del segundo objeto, y D y E son vectores unitarios en las direcciones de movimiento de cada partícula, respectivamente, entonces la velocidad del primer objeto, como se ve por el segundo objeto es
Del mismo modo,
Cuando ambos objetos se mueven en la misma dirección, esta ecuación se puede simplificar a
O, haciendo caso omiso de dirección, la diferencia puede ser dado en términos de sólo la velocidad:
Aceleración
La aceleración , o la tasa de cambio de la velocidad, es el derivado de la velocidad con respecto al tiempo (la segunda derivada de la posición con respecto al tiempo) o
La aceleración puede surgir de un cambio con el tiempo de la magnitud de la velocidad o de la dirección de la velocidad o ambos. Si sólo la magnitud v de la velocidad disminuye, esto se refiere a veces como la desaceleración, pero en general, cualquier cambio en la velocidad con el tiempo, incluyendo la desaceleración, se refiere simplemente como la aceleración.
Fuerzas; La segunda ley de Newton
Newton fue el primero en expresar matemáticamente la relación entre la fuerza y el ímpetu . Algunos físicos interpretan segunda ley del movimiento de Newton como una definición de la fuerza y la masa, mientras que otros consideran que es un postulado fundamental, una ley de la naturaleza. De cualquier interpretación tiene las mismas consecuencias matemáticas, históricamente conocido como "La Segunda Ley de Newton":
La cantidad m v se llama el ( canónica) impulso . La fuerza neta sobre una partícula es por lo tanto igual a la tasa de cambio de impulso de la partícula con el tiempo. Dado que la definición de aceleración es a = d v / d t, la segunda ley puede escribirse en forma simplificada y más familiar:
Mientras se conoce la fuerza que actúa sobre una partícula, la segunda ley de Newton es suficiente para describir el movimiento de una partícula. Una vez que las relaciones independientes para cada fuerza que actúa sobre una partícula están disponibles, pueden ser sustituidos en la segunda ley de Newton para obtener una ecuación diferencial ordinaria , que se llama la ecuación de movimiento.
Como ejemplo, supongamos que la fricción es la única fuerza que actúa sobre la partícula, y que puede ser modelado como una función de la velocidad de la partícula, por ejemplo:
donde λ es una constante positiva. Entonces la ecuación de movimiento es
Esto puede ser integrada para obtener
donde v 0 es la velocidad inicial. Esto significa que la velocidad de esta partícula decae exponencialmente a cero a medida que avanza el tiempo. En este caso, un punto de vista equivalente es que la energía cinética de la partícula es absorbida por la fricción (que la convierte en calor la energía de acuerdo con la conservación de la energía), frenarla. Esta expresión puede integrarse adicionalmente para obtener la posición r de la partícula como una función del tiempo.
Fuerzas importantes incluyen la fuerza de la gravedad y la Fuerza de Lorentz para el electromagnetismo . Además, la tercera ley de Newton a veces se puede utilizar para deducir las fuerzas que actúan sobre una partícula: si se sabe que la partícula A ejerce una fuerza F sobre otra partícula B, se deduce que B debe ejercer una fuerza de reacción igual y opuesta, - F , en A. La forma fuerte de la tercera ley de Newton requiere que F y - F acto lo largo de la línea que une A y B, mientras que la forma débil no lo hace. Ilustraciones de la forma débil de la tercera ley de Newton se encuentran a menudo por fuerzas magnéticas.
Trabajo y energía
Si una fuerza constante F se aplica a una partícula que logra un desplazamiento Δ r, el trabajo realizado por la fuerza se define como la producto escalar de los vectores de fuerza y desplazamiento:
Más en general, si la fuerza varía como una función de la posición que la partícula se mueve de r a r 1 2 a lo largo de una trayectoria C, el trabajo realizado sobre la partícula está dada por la integral de línea
Si el trabajo realizado en el movimiento de la partícula de R 1 a R 2 es el mismo sin importar qué camino le consta a la fuerza se dice que es conservador. La gravedad es una fuerza conservadora, como es la fuerza debida a una idealizada primavera, como se da por La ley de Hooke. La fuerza debida a la fricción es no conservadora.
La energía cinética E k de una partícula de masa m que viaja a la velocidad v está dada por
Para objetos extendidos compuestos por muchas partículas, la energía cinética del cuerpo compuesto es la suma de las energías cinéticas de las partículas.
El teorema de trabajo-energía establece que para que una partícula de masa constante m el trabajo total W realizado sobre la partícula de posición r 1 r 2 es igual a la variación de la energía cinética E k de la partícula:
Las fuerzas conservadoras se pueden expresar como la gradiente de una función escalar, conocido como el energía potencial y denotado E p:
Si todas las fuerzas que actúan sobre una partícula son conservadores, y E p es el total energía potencial (que se define como una obra de fuerzas involucradas para reorganizar posiciones mutuas de los órganos), que se obtiene sumando las energías potenciales correspondientes a cada fuerza
Este resultado se conoce como la conservación de la energía y establece que el total de la energía ,
es constante en el tiempo. A menudo es útil, porque muchas fuerzas comúnmente encontrados son conservadoras.
Más allá de las leyes de Newton
La mecánica clásica también incluye descripciones de los complejos movimientos de los objetos no puntuales extendidas. Leyes de Euler proporcionan extensiones a las leyes de Newton en este ámbito. Los conceptos de momento angular se basan en el mismo cálculo se utiliza para describir el movimiento unidimensional. La ecuación cohete se extiende el concepto de velocidad de cambio de impulso de un objeto para incluir los efectos de un objeto "pérdida de masa".
Hay dos importantes formulaciones alternativas de la mecánica clásica: Mecánica lagrangiana y Mecánica hamiltoniana. Estas, y otras formulaciones modernas, por lo general pasan por alto el concepto de "fuerza", en vez refiriéndose a otras magnitudes físicas, como la energía, la velocidad y el momento, para la descripción de los sistemas mecánicos en coordenadas generalizadas.
Las expresiones dadas anteriormente para el impulso y la energía cinética sólo son válidos cuando no hay una contribución significativa electromagnética. En el electromagnetismo, la segunda ley de Newton para cables conductores de corriente se rompe menos uno incluye la contribución del campo electromagnético al impulso del sistema según lo expresado por el Vector de Poynting divide por 2 c, donde c es la velocidad de la luz en el espacio libre.
Límites de validez

Muchas ramas de la mecánica clásica son simplificaciones o aproximaciones de las formas más exactos; dos de los más precisos siendo la relatividad general y relativistas mecánica estadística . La óptica geométrica es una aproximación a la la teoría cuántica de la luz, y no tiene una forma "clásica" superior.
La aproximación newtoniana a la relatividad especial
En la relatividad especial, el momento de una partícula viene dada por
donde m es la masa en reposo de la partícula, v su velocidad, y c es la velocidad de la luz.
Si v es muy pequeño en comparación con c, v 2 / c 2 es aproximadamente cero, y así
Así, la ecuación newtoniana p = m v es una aproximación de la ecuación relativista para cuerpos que se mueven con velocidades bajas en comparación con la velocidad de la luz.
Por ejemplo, la frecuencia de ciclotrón relativista de una ciclotrón, girotrón, o de alta tensión magnetrón está dada por
donde f es la frecuencia c clásica de un electrón (o de otra partícula cargada) con cinética de energía y T ( descanso) masa m 0 rodeando en un campo magnético. El (resto) masa de un electrón es 511 keV. Así que la corrección de la frecuencia es de 1% para un tubo de vacío magnético con una tensión de corriente continua 5,11 kV de aceleración.
La aproximación clásica a la mecánica cuántica
El modelo de rayos de la mecánica clásica se rompe cuando el longitud de onda de De Broglie no es mucho menor que otras dimensiones del sistema. Para partículas no relativistas, esta longitud de onda es
donde h es P constante de Planck es el impulso.
Una vez más, esto ocurre con los electrones antes de que suceda con las partículas más pesadas. Por ejemplo, los electrones utilizados por Clinton Davisson y Lester Germer en 1927, acelerado por 54 voltios, tenía una longitud de onda de 0.167 nm, lo que fue suficiente para exhibir un solo difracción lóbulo lateral al reflexionar desde la cara de una moneda de cristal con un espaciado atómico de 0.215 nm. Con un mayor cámara de vacío, parecería relativamente fácil de aumentar la resolución angular de todo un radian a una difracción cuántica miliradián y ver en los patrones periódicos de circuito integrado de memoria del ordenador.
Los ejemplos más prácticos del fracaso de la mecánica clásica en una escala de ingeniería son la conducción por túnel cuántico en diodos túnel y muy estrecho transistor puertas en circuitos integrados .
La mecánica clásica es el mismo extremo aproximación de alta frecuencia como la óptica geométrica. Es más a menudo precisa porque describe partículas y cuerpos con masa en reposo. Estos tienen más impulso y por lo tanto más cortas longitudes de onda de De Broglie que las partículas sin masa, como la luz, con las mismas energías cinéticas.
Ramas
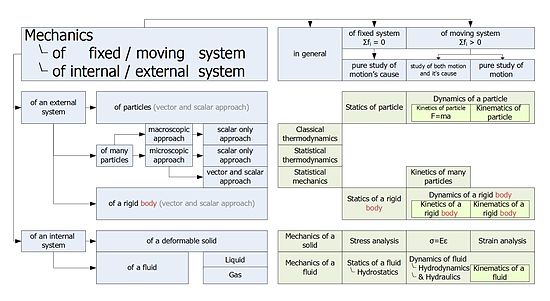
La mecánica clásica fue dividido tradicionalmente en tres ramas principales:
- Estática, el estudio de equilibrio y su relación con las fuerzas
- Dinámica, el estudio del movimiento y su relación con las fuerzas
- Cinemática , frente a las consecuencias de movimientos observados sin tener en cuenta las circunstancias causándoles
Otra división se basa en la elección de formalismo matemático:
- Mecánica newtoniana
- Mecánica lagrangiana
- Mecánica hamiltoniana
Alternativamente, una división puede ser hecha por región de aplicación:
- La mecánica celeste, en relación con estrellas , planetas y otros cuerpos celestes
- Mecánica de medios continuos, para materiales modelados como un proceso continuo, por ejemplo, sólidos y líquidos (es decir, los líquidos y los gases ).
- Mecánica relativista (es decir, incluyendo los especiales y generales teorías de la relatividad), para los órganos cuya velocidad cercana a la velocidad de la luz.
- La mecánica estadística , que proporciona un marco para relacionar las propiedades microscópicas de los átomos y moléculas individuales a los macroscópicos o granel termodinámicas propiedades de los materiales.