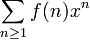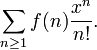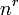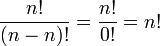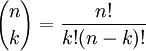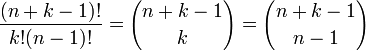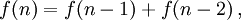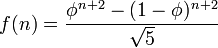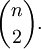Combinatoria

Temas relacionados: Matemáticas

Acerca de este escuelas selección Wikipedia

SOS Children han producido una selección de artículos de la Wikipedia para escuelas desde 2005. Una buena manera de ayudar a otros niños es mediante el patrocinio de un niño

Combinatoria es una rama de matemáticas puras concerniente al estudio de discreta (y por lo general objetos finitos). Se relaciona con muchas otras áreas de las matemáticas , como el álgebra , teoría de la probabilidad , teoría ergódica y geometría , así como a los sujetos aplicadas en ciencias de la computación y la física estadística. Aspectos de la combinatoria incluyen "contar" los objetos que cumplan con ciertos criterios ( combinatoria enumerativa), decidir cuando se puedan cumplir los criterios, y la construcción y análisis de objetos que satisfacen los criterios (como en diseños combinatorios y teoría matroid), encontrar, u objetos "más grandes" "más pequeños" "óptimas" ( combinatoria extremal y optimización combinatoria), y encontrar algebraicas estructuras estos objetos pueden tener ( combinatoria algebraica).

Combinatoria es tanto sobre la resolución de problemas como la construcción de teorías, aunque ha desarrollado métodos teóricos potentes, sobre todo desde finales del siglo XX (ver la página Lista de combinatoria temas para los detalles de la evolución más reciente de la asignatura). Una de las partes más antiguas y más accesibles de la combinatoria es la teoría de grafos, que también tiene numerosas conexiones naturales a otros ámbitos.

Hay muchos patrones combinatorios y teoremas relacionados con la estructura de los conjuntos combinatorios. Estos a menudo se centran en un partición o partición ordenada de un conjunto. Vea el Lista de los asuntos de partición para una lista ampliada de temas relacionados o del Lista de combinatoria temas para obtener una lista más general. Algunos de los resultados más notables se destacan a continuación.

Un ejemplo de una pregunta combinatoria simple es la siguiente: ¿Cuál es el número de ordenaciones posibles de una baraja de 52 cartas distintas? La respuesta es 52! (52 factorial ), que es igual a aproximadamente 8,0658 × 10 ^67.

Otro ejemplo de un problema más difícil: Dado un cierto número n de personas, es posible asignar a los conjuntos de modo que cada persona está en al menos un conjunto, cada par de personas es exactamente de un juego juntos, cada dos conjuntos tienen exactamente una persona en común, y ningún conjunto contiene a todos, todas menos una persona, o exactamente una persona? La respuesta depende de n. Consulte " La teoría del diseño "a continuación.

Combinatoria se utiliza con frecuencia en la informática para obtener estimaciones sobre el número de elementos de ciertos conjuntos. Un matemático que estudia la combinatoria se refiere a menudo como un combinatorialist o combinatorist.

Historia de Combinatoria

Usos más tempranos

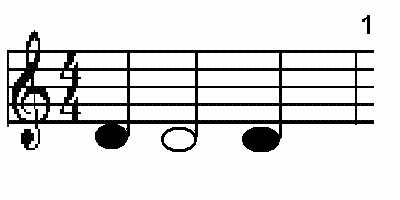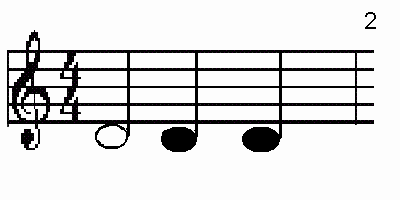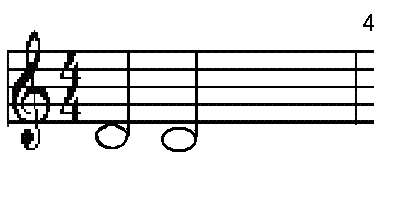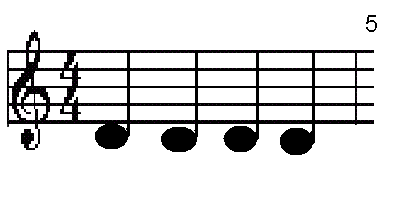
La aparición del número de Fibonacci cinco en la prosodia. Hay una manera de organizar un golpe, dos por dos, tres por tres, y cinco para cuatro tiempos.

Los primeros libros sobre la combinatoria son de la India. La Texto jainista, el Bhagabati Sutra, tuvo la primera mención de un problema de combinatoria; se preguntó cuántas maneras se podría tomar seis sabores uno, dos, o tres sabores a la vez. El Bhagabati Sutra fue escrito alrededor del año 300 aC, y por lo tanto era el primer libro para hablar de la función de elección . Las siguientes ideas de Combinatoria vinieron de Pingala, que estaba interesado en prosodia. En concreto, quería saber cuántas maneras un metro sílaba seis se podría hacer de notas cortas y largas. Escribió este problema en el sutra Chanda (también Chandahsutra) en el segundo siglo antes de Cristo. Además, también encontró el número de metros que tenían notas n largos y k notas cortas, lo cual es equivalente a encontrar los coeficientes binomiales.

Las ideas de la Bhagabati se generalizaron por el matemático indio Mahariva en 850 dC, y la obra de Pingala en la prosodia se amplió por Bhaskara y Hemacandra en 1100 AD. Bhaskara fue la primera persona conocida para encontrar la función de elección generalizada, aunque Brahmagupta pudo haber conocido antes. Preguntó Hemacandra cómo existían muchos metros de una cierta longitud si una nota larga se consideró dos veces más que una breve nota, lo que equivale a la búsqueda de los números de Fibonacci.

Un hexagrama

Mientras que la India fue el primer país en publicar los resultados en Combinatoria, hubo descubrimientos de otras naciones sobre temas similares. La conexión más antiguo conocido de Combinatoria proviene de la Papiro Rhind, problema 79, para la implementación de una serie geométrica. El siguiente hito se lleva a cabo por el I Ching . El libro es acerca de lo que significan los diferentes hexagramas, y para hacer esto que necesitaban saber cuántos hexagramas posible existían. Dado que cada hexagrama es una permutación con repeticiones de seis líneas, donde cada línea puede ser de dos estados, sólidas o discontinuas, la combinatoria de producir el resultado que su son 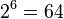$2 ^ 6 = 64$ hexagramas. Un monje también puede haber contado el número de configuraciones para un juego similar al Ir alrededor de 700 dC. Aunque China tenía relativamente pocos avances en la combinatoria enumerativa, resolvieron un problema de diseño combinatoria, el cuadrado mágico , alrededor de 100 dC.

En Grecia, Plutarco escribió que los Jenócrates descubrieron el número de sílabas diferentes posibles en el idioma griego. Esto, sin embargo, es poco probable porque esta es una de las pocas menciones de Combinatoria en Grecia. El número de los que encontraron, 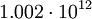$1.002 \ cdot 10 ^ {12}$ También parece demasiado redondo para ser más que una conjetura. .

Cuadrados mágicos mantuvieron un interés de China, y comenzaron a generalizar su plaza original de 3 × 3 entre 900 y 1300 dC. China, mantuvo correspondencia con el Medio Oriente sobre este problema en el siglo 13. El Medio Oriente también se enteró de coeficientes binomiales de obra india, y encontró la conexión a la expansión polinómica.

Combinatoria en Occidente

Combinatoria llegó a Europa en el siglo 13 a través de dos matemáticos, Leonardo Fibonacci y Jordanus Nemorarius. Fibonacci de Líber Abad introdujo muchos de los árabes e indias ideas para Europa, incluido el de los números de Fibonacci. Jordanus fue la primera persona para arreglar el coeficiente binomial de un triángulo, como lo hizo en la proposición 70 de De la Aritmética. Esto se hizo también en el Oriente Medio en 1265, y China alrededor de 1300. Hoy, este triángulo es conocido como el triángulo de Pascal.

La contribución de Pascal al triángulo que lleva su nombre se debe a su trabajo en pruebas formales al respecto, además de su conexión entre ella y la probabilidad. Junto con Leibniz y sus ideas acerca de las particiones en el siglo 17, son considerados los fundadores de la combinatoria modernas.

Tanto Pascal y Leibniz entendieron que el álgebra y la combinatoria correspondían (aka, la expansión binomial fue equivalente a la función de la elección). Esto fue ampliado por De Moivre, que encontró la expansión de una multinomial. De Moivre también encontró la fórmula para desarreglos utilizando el principio de inclusión-exclusión, un método diferente de Nikolaus Bernoulli, que los había encontrado previamente. Se las arregló para aproximar la coeficientes binomiales y factorial. Finalmente, encontró una forma cerrada para los números de Fibonacci inventando funciones generadoras.

En el siglo 18, Euler trabajó en problemas de combinatoria. Además de trabajar en varios problemas de probabilidad que enlazan con la combinatoria, trabajó en la gira caballeros, Cuadrado grecolatino, Número de Euler, y otros. También inventó la teoría de grafos resolviendo el Siete Puentes de Königsberg problema, que también conducen a la formación de topología . Por último, dio la palada inicial con particiones por el uso de funciones generadoras.

Combinatoria enumerativa

Contar el número de formas en que ciertos patrones se pueden formar es el problema central de la combinatoria enumerativa. Dos ejemplos de este tipo de problema están contando combinaciones y permutaciones contando (como se discutió en la sección anterior). Más en general, dada una colección infinita de conjuntos finitos _{i} S indexadas por los números naturales , combinatoria enumerativa pretende describir una función de recuento que cuenta el número de objetos en S _n para cada n. Aunque contar el número de elementos en un conjunto es una bastante amplia problema matemático, muchos de los problemas que surgen en aplicaciones tienen un relativamente simple descripción combinatoria.

Los más simples tales funciones son fórmulas cerradas, que se pueden expresar como una composición de funciones elementales como factoriales , poderes, y así sucesivamente. Por ejemplo, como se muestra a continuación, el número de diferentes ordenaciones posibles de una baraja de cartas n es f (n) = n!. A menudo, no hay forma cerrada está disponible inicialmente. En estos casos, con frecuencia primero derivamos una relación de recurrencia, a continuación, resolvemos la recurrencia de llegar a la forma cerrada deseada.

Finalmente, f (n) puede ser expresado por una series formales, llamado su función generatriz, que es más comúnmente ya sea la función generadora ordinaria

$\ Sum_ {n \ ge 1} f (n) x ^ n$

o la función de generación exponencial

$\ Sum_ {n \ ge 1} f (n) \ frac {x ^ n} {n!}.$

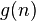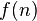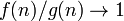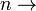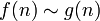A menudo, una fórmula cerrada complicado dan poca información acerca del comportamiento de la función de cuenta como el número de objetos contados crece. En estos casos, un simple aproximación asintótica puede ser preferible. Una función $g (n)$ es una aproximación asintótica a $f (n)$ si $f (n) / g (n) \ rightarrow 1$ como $n \ rightarrow$ el infinito . En este caso, escribimos $f (n) (n) \ \ sim g,$ .

Una vez determinada, la función generadora puede permitir uno para extraer toda la información dada por los enfoques anteriores. Además, las diversas operaciones naturales en la generación de funciones tales como suma, multiplicación, diferenciación, etc., tienen un significado combinatoria; esto le permite a uno extienden los resultados de un problema combinatorio para resolver otros.

Permutaciones con repetición

Cuando la orden importa, y un objeto se puede elegir más de una vez, el número de permutaciones es

$n ^ r \, \!$

donde n es el número de objetos de los que puede elegir y R es el número a ser elegido.

Por ejemplo, si usted tiene las letras A, B, C y D y de que deseen descubrir el número de maneras de organizar en tres patrones de letras ( trigramas)

cuestiones de orden (por ejemplo, AB es diferente de BA, ambos están incluidos como posibilidades)
un objeto se puede elegir más de una vez (AA posible)

usted encontrará que hay 4 ³ o 64 maneras. Esto se debe a que por primera ranura que puede elegir cualquiera de los cuatro valores, por la segunda ranura se puede elegir cualquiera de los cuatro, y para la ranura final que usted puede elegir cualquiera de las cuatro letras. Multiplicando juntos da el total.

Permutaciones sin repeticiones

Cuando las cuestiones de orden y cada objeto se pueden elegir sólo una vez, entonces el número de permutaciones es

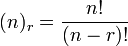$(N) _ {r} = \ frac {n!} {(N-r)!}$ donde n es el número de objetos de los que usted puede elegir, r es el número a ser elegido y "!" es el símbolo estándar significa factorial .

Por ejemplo, si usted tiene a cinco personas y se va a elegir tres de estos, usted tendrá 5 / (5-3)! = 60 permutaciones.

Tenga en cuenta que si n = r (es decir, el número de elementos elegidos es igual al número de elementos para elegir, cinco personas y recoger los cinco), entonces la fórmula se convierte

$\ Frac {n!} {(N-n)!} = \ Frac {n!} {0!} = N!$

donde 0! = 1.

Por ejemplo, si usted tiene las mismas cinco personas y desea saber cuántas maneras puede organizarlos, sería 5! o 5 × 4 × 3 × 2 × 1 = 120 maneras. La razón de esto es que usted puede elegir entre 5 para la ranura inicial, entonces se quedan con sólo 4 a elegir para la segunda ranura etc. Multiplicando juntos da el total de 120.

Combinaciones sin repeticiones

Cuando el orden no importa y cada objeto se puede elegir sólo una vez, el número de combinaciones es el coeficiente binomial :

${N \ choose k} = {{n} \ over {k! (N - k)}!}$

donde n es el número de objetos de los que puede elegir y K es el número a ser elegido.

Por ejemplo, si usted tiene diez números y desea elegir 5 tendrías 10 / (5 (10 -!! 5))! = 252 maneras de elegir. El coeficiente binomial también se utiliza para calcular el número de permutaciones en una lotería.

Las combinaciones con repeticiones

Cuando el orden no importa y un objeto se puede elegir más de una vez, entonces el número de combinaciones es

${{(N + k - 1)!} \ Over {k (n - 1)!}!} = {{N + k - 1} \ seleccione {k}} = {{n + k - 1} \ elegir {n - 1}}$

donde n es el número de objetos de los que puede elegir y K es el número a ser elegido.

Por ejemplo, si usted tiene diez tipos de rosquillas (n) en un menú para elegir y quiere tres donas (k) existen (10 + 3 - 1)! / 3 (10 - 1)! = 220 maneras de elegir (ver también multiset).

Los números de Fibonacci

Sea f (n) ser el número de distintos subconjuntos del conjunto 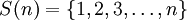$S (n) = \ {1,2,3, \ ldots, n \}$ que no contienen dos enteros consecutivos. Cuando n = 4, tenemos los conjuntos {}, {1}, {2}, {3}, {4}, {1,3}, {1,4}, {2,4}, por lo que f (4 ) = 8. Contamos con los subconjuntos deseados de 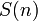$S (n)$ contando por separado los subconjuntos que contienen elemento 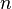$n$ y aquellos que no lo hacen. Si un subconjunto contiene 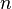$n$ , A continuación, que no contiene elemento 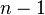$n-1$ . Así que no son exactamente 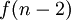$f (n-2)$ de los subconjuntos deseados que contienen elemento 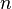$n$ . El número de subconjuntos que no contienen 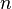$n$ es simplemente 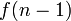$f (n-1)$ . La incorporación de estos números juntos, obtenemos la relación de recurrencia:

$f (n) = f (n-1) + f (n-2) \,,$

donde $f (1) = 2$ y $f (2) = 3$ .

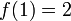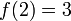Ya en 1202, Leonardo Fibonacci estudió estos números. Ahora se llaman números de Fibonacci ; en particular, 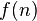$f (n)$ se conoce como el 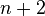$n + 2$ nd número de Fibonacci. Aunque la relación de recurrencia nos permite calcular todos los números de Fibonacci, el cálculo es ineficiente. Sin embargo, mediante el uso de técnicas estándar para resolver relaciones de recurrencia, que pueden llegar a la solución de forma cerrada:

$f (n) = \ frac {\ phi ^ {n + 2} - (1- \ phi) ^ {n + 2}} {\ sqrt {5}}$

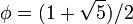donde $\ Phi = (1 + \ sqrt 5) / 2$ , La proporción áurea .

En el ejemplo anterior, una aproximación asintótica a 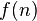$f (n)$ es:

$f (n) \ sim \ frac {\ phi ^ {n + 2}} {\ sqrt {5}}$

como n se hace grande.

Combinatoria Estructurales

La teoría de grafos

Los gráficos son objetos básicos en combinatoria. Las preguntas van desde contar (por ejemplo, el número de gráficos de n vértices con bordes k) estructural (por ejemplo, que contienen gráficos Ciclos hamiltonianos).

La teoría del diseño

Un simple resultado de la el área de diseño de bloques de la combinatoria es que el problema de los conjuntos que forman, descrito en la introducción, tiene una solución sólo si n tiene la forma q ² + q + 1. Es menos sencillas para demostrar que existe una solución si q es una Potencia primaria. Se conjetura que estas son las únicas soluciones. Se ha demostrado, además, que si existe una solución para q congruente con 1 o 2 mod 4, entonces q es una suma de dos números cuadrados. Este último resultado, la Bruck-Ryser teorema, se prueba por una combinación de métodos constructivos basados en campos finitos y una aplicación de formas cuadráticas.

Cuando no existe una estructura tal, se denomina finito plano proyectivo; mostrando así cómo geometría finita y la combinatoria se cruzan.

Teoría Matroid

Teoría Matroid abstrae parte de la geometría . Se estudia las propiedades de conjuntos (por lo general, conjuntos finitos) de vectores en un espacio vectorial que no dependen de los coeficientes particulares en una relación de dependencia lineal. No sólo la estructura, sino también propiedades enumerativos pertenecen a Matroid teoría.

Por ejemplo, dado un conjunto de n vectores en el espacio euclidiano , ¿cuál es el mayor número de aviones que pueden generar? Respuesta: el coeficiente binomial

$\ Binom {n} {2}.$

¿Hay un conjunto que genera exactamente un plano menos? (No, en casi todos los casos.) Estas son preguntas extremales en la geometría, como veremos a continuación.

Extremal y combinatoria probabilistas

Muchas de las preguntas se refieren a extremales sistemas establecidos. Un ejemplo simple es la siguiente: ¿cuál es el mayor número de subconjuntos de un n -element establecer que uno puede tener, si no dos de los subconjuntos son disjuntos? Respuesta: la mitad del número total de legajos. Prueba: Llame a la n conjunto -element S. Entre cualquier subconjunto T y su complementar S - T, como mucho uno puede ser elegido. Esto demuestra el número máximo de subconjuntos seleccionados no es mayor que la mitad del número de subconjuntos. Para mostrar uno puede alcanzar la mitad del número, elegir un elemento x de S y elegir todos los subconjuntos que contienen x.

Un problema más difícil es caracterizar las soluciones extremales; en este caso, para mostrar que no hay otra opción de subconjuntos puede alcanzar el número máximo tiempo que satisface el requisito.

A menudo es muy difícil, incluso para encontrar la respuesta extremal f (n) exactamente y uno sólo puede dar una estimación asintótica.

Teoría de Ramsey

Teoría de Ramsey es una parte célebre de la combinatoria extremal. Declara que toda suficientemente grande configuración aleatoria contendrá algún tipo de orden.

Frank P. Ramsey demostró que para cada entero k no es un entero n, tal que cada gráfico de n vértices o bien contiene una camarilla o un conjunto independiente de tamaño k. Este es un caso especial de Teorema de Ramsey. Por ejemplo, dado cualquier grupo de seis personas, siempre es el caso de que uno puede encontrar a tres personas de este grupo que, o bien todos se conocen entre sí o no todos se conocen entre sí. La clave de la prueba en este caso es la Principio del palomar: o A conoce a tres de las personas restantes, o A no sabe tres de las personas restantes.

Aquí está una prueba simple: Tome una de las seis personas, lo llaman A. O bien A conoce a tres de las personas restantes, o A no sabe tres de las personas restantes. Supongamos que la primera (la prueba es idéntica si asumimos este último). Deje que las tres personas que A sabe ser B, C y D. Ahora bien dos personas de {B, C, D} conocerse (en cuyo caso tenemos un grupo de tres personas que se conocen entre sí - estos dos, más un ) o ninguno de B, C, D conocerse (en cuyo caso tenemos un grupo de tres personas que no se conocen entre sí - B, C, D). QED.

Combinatoria extremal

Los tipos de preguntas formuladas en este caso son de la más grande gráfica posible que satisface ciertas propiedades. Por ejemplo, el más grande gráfico sin triángulos en 2n vértices es un grafo bipartito completo K _{n, n.}

Combinatoria probabilistas

Aquí las preguntas son del tipo siguiente: ¿cuál es la probabilidad de que una determinada propiedad gráfica de un gráfico aleatorio (dentro de una cierta clase) Por ejemplo, ¿cuál es el número medio de triángulos en un gráfico de azar?

Combinatoria geométricos

Combinatoria geométrica está relacionada con convexa y geometría discreta. Se pregunta, por ejemplo, el número de caras de cada dimensión puede un politopo convexo tienen. Propiedades métricas de politopos juegan un papel importante, así, por ejemplo, la Cauchy teorema sobre la rigidez de politopos convexos. Politopos especiales también se consideran, por ejemplo, permutohedron, associahedron y Polytope Birkhoff.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Combinatorics&oldid=197264587 "

We provide Linux to the World