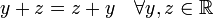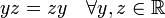Propiedad conmutativa
Acerca de este escuelas selección Wikipedia
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . ¿Quieres saber sobre el patrocinio? Ver www.sponsorachild.org.uk
Conmutatividad es un ampliamente utilizado matemática término que se refiere a la capacidad de cambiar el orden de algo sin cambiar el resultado final. Es una propiedad fundamental en la mayoría de las ramas de las matemáticas y muchas pruebas dependen de él. La conmutatividad de operaciones simples fue durante muchos años asumió implícitamente y la propiedad no se le dio un nombre o atribuyó hasta el siglo 19, cuando los matemáticos empezaron a formalizar la teoría de las matemáticas.
Los usos más comunes
La propiedad conmutativa (o ley conmutativa) es una propiedad asociada con operaciones y binarios funciones . Del mismo modo, si la propiedad conmutativa se mantiene para un par de elementos bajo una cierta operación binaria entonces se dice que los dos elementos conmutan bajo esa operación.
En grupo y la teoría de conjuntos , muchas estructuras algebraicas se llaman conmutativa cuando ciertos operandos satisfacen la propiedad conmutativa. En altas ramas de las matemáticas, como el análisis y el álgebra lineal la conmutatividad de las operaciones conocidas (como la adición y la multiplicación se utiliza en los números reales y complejos) a menudo (o implícitamente supone) en pruebas.
Definiciones matemáticas
El término "conmutativa" se utiliza en varios sentidos relacionados.
1. A operación binaria * en un conjunto S se dice que es conmutativo si:
- x * y = y * x para cada x, y ∈ S
- Una operación que no satisface la propiedad anterior se llama conmutativa.
2. Se dice que x conmuta con y bajo * si:
- x * y = y * x
3. A función binaria f: A × A → B se dice que es conmutativo si:
- f (x, y) = f (y, x) para cada x, y ∈ A.
Historia y etimología

Récords del uso implícito de la propiedad conmutativa se remontan a tiempos antiguos. Los egipcios utilizaron la propiedad conmutativa de la multiplicación para simplificar la computación productos. Euclides es conocido por haber asumido la propiedad conmutativa de la multiplicación en su libro Elementos . Usos formales de la propiedad conmutativa surgieron a finales del 18 y principios del siglo 19, cuando los matemáticos comenzaron a trabajar en una teoría de funciones. Hoy en día la propiedad conmutativa es una propiedad bien conocida y básico que se utiliza en la mayoría de las ramas de las matemáticas. Versiones simples de la propiedad conmutativa se enseña generalmente en el inicio de los cursos de matemáticas.
El primer uso de la conmutativa real plazo fue en un libro de memorias por Francois Servois en 1814, que utilizó la palabra commutatives al describir las funciones que tienen lo que ahora se denomina la propiedad conmutativa. La palabra es una combinación de la palabra francesa cercanías significado "para sustituir o interruptor" y el sufijo significado -ative "tiende a" por lo que la palabra significa literalmente "que tiende a sustituir o switch." El término entonces apareció en Inglés en Philosophical Transactions de la Royal Society en 1844.
Inmuebles relacionados
Asociatividad
La propiedad asociativa está estrechamente relacionada con la propiedad conmutativa. La propiedad asociativa establece que el orden en que se realizan las operaciones no afecta el resultado final. En contraste, la propiedad conmutativa establece que el orden de los términos no afecta el resultado final.
Simetría
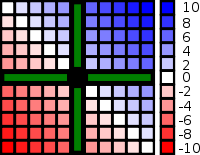
La simetría puede estar directamente relacionado con la conmutatividad. Cuando un operador conmutativo está escrito como una función binaria entonces la función resultante es simétrica al otro lado de la línea y = x. Como ejemplo, si permitimos que una función f representan adición (una operación conmutativa) de manera que f (x, y) = x + y entonces f es una función simétrica que se puede ver en la imagen de la derecha.
Ejemplos
Operaciones conmutativa en la vida cotidiana
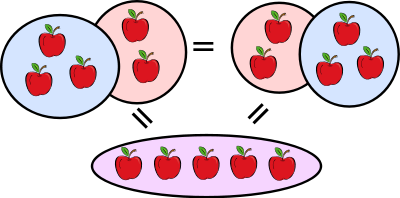
- De ponerse los zapatos se asemeja a una operación conmutativa, ya que no importa si usted pone el zapato izquierdo o derecho en primer lugar, el resultado final (que tiene dos zapatos), es el mismo.
- Al hacer el cambio aprovechamos la conmutatividad de la suma. No importa qué orden ponemos el cambio en el, siempre se suma al mismo total.
Operaciones conmutativas en matemáticas
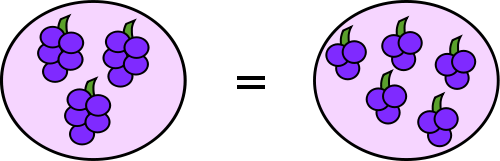
Dos ejemplos bien conocidos de operaciones binarias conmutativas son:
- La adición de los números reales , que es conmutativa desde
- Por ejemplo 4 + 5 + 5 = 4, ya que ambos expresiones equivalen a 9.
- La multiplicación de números reales , que es conmutativa desde
- Por ejemplo, 3 × 5 = 5 × 3, ya que ambas expresiones son iguales a 15.
- Otros ejemplos de operaciones binarias conmutativas incluyen la adición y multiplicación de números complejos , la adición de vectores , y la intersección y unión de conjuntos.
Operaciones no conmutativa en la vida cotidiana

- Lavado y secado de su ropa se parece a una operación conmutativa, si seca y luego se lava, se obtiene un resultado significativamente diferente que si se lava primero y luego seca.
- El Cubo de Rubik es conmutativa. Por ejemplo, girando la cara hacia la derecha delantera, la cara superior hacia la derecha y la cara frontal izquierda (FUF) no da el mismo resultado que torcer la cara frontal hacia la derecha y luego hacia la izquierda y finalmente torcer arriba en sentido horario (FF'U). Los giros no conmutan. Esto se estudia en la teoría de grupos .
Operaciones no conmutativa en matemáticas
Algunas operaciones binarias no conmutativos son:
- resta es no conmutativa desde
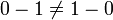
- división es no conmutativa desde
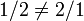
- matriz de la multiplicación es conmutativa desde
Las estructuras matemáticas y conmutatividad
- Una grupo abeliano es un grupo cuya operación del grupo es conmutativa.
- Un anillo conmutativo es un anillo cuya multiplicación es conmutativa. (Adición de un anillo es, por definición, siempre conmutativa.)
- En un campo tanto la suma y la multiplicación son conmutativa.
- La centro es el mayor subconjunto conmutativa de un grupo.