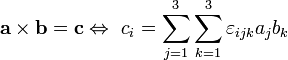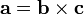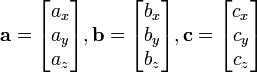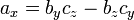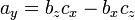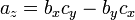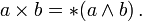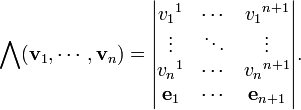Producto de la Cruz
Antecedentes
Esta selección se hace para las escuelas por caridad para niños leer más . Con Infantil SOS se puede elegir a apadrinar a los niños en más de cien países
En matemáticas , el producto vectorial es un operación binaria en dos vectores en un tridimensional espacio euclidiano que resulta en otro vector que es perpendicular a los dos vectores de entrada. Por el contrario, la producto escalar produce una resultado escalar. En muchos problemas de ingeniería y física, es útil ser capaz de construir un vector perpendicular a partir de dos vectores existentes, y el producto cruzado proporciona un medio para hacerlo. El producto cruz también se conoce como el producto vectorial, o Gibbs producto vectorial.
El producto cruz no se define, excepto en tres dimensiones (y el álgebra definido por el producto cruz no es asociativo ). Al igual que el producto de punto, que depende de la métrica del espacio euclidiano. A diferencia de la producto escalar, sino que también depende de la elección de orientación o "lateralidad". Ciertas características del producto vectorial se pueden generalizar a otras situaciones. Para opciones arbitrarias de orientación, el producto vectorial no debe considerarse como un vector, sino como un pseudovector. Para opciones arbitrarias de métrica, y en dimensiones arbitrarias, el producto vectorial se puede generalizar por la producto exterior de los vectores, definiendo una dos-forma en lugar de un vector.
Definición
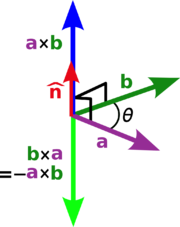
El producto vectorial de dos vectores a y b se denota por a × b. En una de tres dimensiones espacio euclidiano , con un usual sistema de la mano derecha de coordenadas , se define como un vector c que es perpendicular tanto a y b, con una dirección dada por el regla de la mano derecha y una magnitud igual al área de la paralelogramo que los vectores se extienden.
El producto cruz está dada por la fórmula
donde θ es la medida de la ángulo entre A y B (0 ° ≤ θ ≤ 180 °), a y b son las magnitudes de los vectores a y b, y 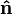 es un vector unitario perpendicular al plano que contiene a y b. Si los vectores a y b son colineales (es decir, el ángulo θ entre ellos es ya sea 0 ° o 180 °), por la fórmula anterior, el producto cruzado de a y b es el vector cero 0.
es un vector unitario perpendicular al plano que contiene a y b. Si los vectores a y b son colineales (es decir, el ángulo θ entre ellos es ya sea 0 ° o 180 °), por la fórmula anterior, el producto cruzado de a y b es el vector cero 0.
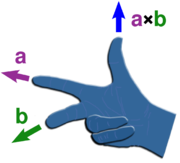
La dirección del vector 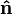 está dada por la regla de la mano derecha, donde se señala simplemente el dedo índice de la mano derecha en la dirección de A y el dedo medio en la dirección de b. Entonces, el vector
está dada por la regla de la mano derecha, donde se señala simplemente el dedo índice de la mano derecha en la dirección de A y el dedo medio en la dirección de b. Entonces, el vector 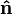 está saliendo del pulgar (ver la foto de la derecha).
está saliendo del pulgar (ver la foto de la derecha).
Uso del producto cruz requiere la imparcialidad del sistema de coordenadas que deben tenerse en cuenta (tan explícito en la definición anterior). Si un sistema de coordenadas de mano izquierda se utiliza, la dirección del vector 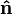 está dada por la regla de la mano izquierda y puntos en la dirección opuesta.
está dada por la regla de la mano izquierda y puntos en la dirección opuesta.
Esto, sin embargo, crea un problema porque la transformación de un sistema de referencia arbitrario a otro (por ejemplo, una transformación de la imagen de espejo de un diestro a un sistema de coordenadas de mano izquierda), no debe cambiar la dirección de 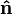 . El problema se aclara en darse cuenta de que el producto cruzado de dos vectores no es un (verdadero) vectores, sino más bien una pseudovector. Ver producto cruz y la prepotencia para más detalle.
. El problema se aclara en darse cuenta de que el producto cruzado de dos vectores no es un (verdadero) vectores, sino más bien una pseudovector. Ver producto cruz y la prepotencia para más detalle.
Cálculo del producto vectorial
Coordinar la notación
La vectores unitarios i, j, k y de la ortogonal determinado sistema de coordenadas de satisfacer las siguientes igualdades:
- i × j = k j × k = i k × i = j.
Con estas reglas, las coordenadas del producto vectorial de dos vectores se pueden calcular fácilmente, sin la necesidad de determinar los ángulos: Let
- a = a 1 i + a 2 j + a 3 k = (a 1, a 2, a 3)
y
- b = b 1 i + b 2 j + b 3 k = (b1, b2, b3)
Entonces
- a × b = (a 2 b 3 - 3 b 2) i + (un 3 b 1 - a 1 b 3) j + (a 1 b 2 - a 2 b 1) k = (a 2 b 3 - un 3 b 2, a 3 b 1 - a 1 b 3, un 1 b 2 - a 2 b 1)
Notación Matrix
La notación de coordenadas también se puede escribir formalmente como el determinante de una matriz :
El determinante de tres vectores se puede recuperar como
- det (a, b, c) = a · (b × c).
Intuitivamente, el producto cruzado puede ser descrita por Esquema Sarrus '. Considere la mesa
Durante los primeros tres vectores unitarios, multiplicar los elementos de la diagonal hacia la derecha (por ejemplo, la primera diagonal contendría i, a 2, y b 3). Durante los últimos tres vectores unitarios, multiplicar los elementos de la diagonal hacia la izquierda y luego negar el producto (por ejemplo, la última diagonal contendría k, a 2, y b 1). El producto cruz se define por la suma de estos productos:
Aunque está escrito aquí en términos de coordenadas, se desprende de la definición geométrica anteriormente que el producto cruz es invariante bajo rotaciones alrededor del eje definido por un × b, y voltea signo bajo el canje de a y b.
Ejemplos
Ejemplo 1
Consideremos dos vectores a = (1,2,3) y B = (4,5,6). El producto una cruz × b es
- a × b = (1,2,3) x (4,5,6) = ((2 × 6 - 3 × 5), - (1 × 6 - 3 × 4), + (1 × 5 - 2 × 4)) = (3,6, -3).
Ejemplo 2
Consideremos dos vectores a = (3,0,0) y B = (0,2,0). El producto una cruz × b es
- a × b = (3,0,0) x (0,2,0) = ((0 × 0-0 × 2), (0 × 0-3 × 0), (3 × 2 - 0, x 0) ) = (0,0,6).
Este ejemplo tiene las siguientes interpretaciones:
- El área del paralelogramo (un rectángulo en este caso) es 2 × 3 = 6.
- El producto cruzado de dos vectores en el plano xy será paralela al eje z.
- Dado que el componente z del resultado es positivo, el ángulo no obtuso de A a B es la izquierda (cuando se observa desde un punto en los semieje Z +, y cuando el sistema de coordenadas es diestro).
Propiedades
Significado geométrico
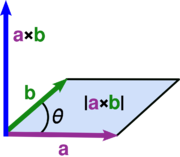
La magnitud del producto cruz puede ser interpretada como la unsigned área de la paralelogramo que tiene a y b como lados:
De hecho, también se puede calcular el volumen V de una paralelepípedo que tiene a, b y c como lados mediante el uso de una combinación de un producto de cruz y un producto de punto, llamado escalar triple producto:
Propiedades algebraicas
El producto cruz es anticonmutativo,
- a × b = - b × a,
distributiva sobre la suma,
- a × (b + c) = (a × b) + (a × c),
y compatible con la multiplicación escalar de manera que
- (Ra) × b = a × (r b) = r (a × b).
No es asociativa , pero satisface la Jacobi identidad:
- a × (b × c) + b × (c × a) + c × (a × b) = 0.
No obedecen al Derecho de cancelación:
- Si a × b = a × c y a ≠ 0, entonces podemos escribir:
- (A × b) - (a × c) = 0 y, por la ley distributiva arriba:
- a × (b - c) = 0
- Ahora, si a es paralelo a (b - c), a continuación, incluso si a ≠ 0 es posible que (b - c) ≠ 0 y por lo tanto que b ≠ c.
Sin embargo, si ambos a · b = a · c y a × b = a × c, entonces podemos concluir que b = c. Ciertamente,
- a. (B - c) = 0, y
- a × (b - c) = 0
de modo que b - c es a la vez paralela y perpendicular al vector distinto de cero a. Esto sólo es posible si b - c = 0.
El distributividad, linealidad y Jacobi espectáculo identidad que R3 junto con la suma de vectores y el producto forma una cruz Acuéstese álgebra.
Además, dos vectores distintos de cero a y b son paralelas si y sólo si a × b = 0.
Expansión Triple producto
La expansión del producto triple, también conocida como la fórmula de Lagrange, es una fórmula que relaciona el producto cruzado de tres vectores (llamado la triple producto vectorial) con el producto escalar:
- a × (b × c) = b (a · c) - c (a · b).
La "BAC menos CAB" mnemotécnica se utiliza para recordar el orden de los vectores en el miembro de la derecha. Esta fórmula se utiliza en la física para simplificar los cálculos del vector. Un caso especial, con respecto gradientes y útiles en cálculo vectorial , es la siguiente.
Este es un caso especial de la más general Operador de Laplace-de Rham 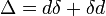 .
.
La siguiente identidad se refiere también al producto cruz y el producto escalar:
Este es un caso especial de la multiplicabilidad 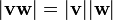 de la norma en el álgebra de cuaternión, y una restricción a
de la norma en el álgebra de cuaternión, y una restricción a 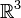 de Identidad de Lagrange.
de Identidad de Lagrange.
Formas alternativas para calcular el producto vectorial
Quaternions
El producto cruz también se puede describir en términos de cuaterniones, y es por eso que las letras i, j, k son una convención para la base estándar en 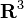 : Se está pensada como los cuaterniones imaginarios.
: Se está pensada como los cuaterniones imaginarios.
Aviso por ejemplo, que las relaciones de productos anteriores dadas cruzadas entre i, j, k, y de acuerdo con las relaciones multiplicativas entre los cuaterniones i, j, k. En general, si representamos un vector [a 1, a 2, a 3] como el cuaternión un 1 i + a 2 j + a 3 k, se obtiene el producto vectorial de dos vectores tomando su producto como cuaterniones y eliminar la parte real del resultado. La parte real será el negativo de la dot producto de los dos vectores.
La conversión a la multiplicación de matrices
Un producto de cruce entre dos vectores (que sólo se puede definir en el espacio tridimensional) se puede reescribir en términos de multiplicación de matrices puro como el producto de una sesgar-simétrica matriz y un vector, como sigue:
donde
Además, si 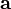 es en sí mismo un producto vectorial:
es en sí mismo un producto vectorial:
entonces
Esta notación proporciona otra manera de generalizar producto cruzado a las dimensiones superiores sustituyendo pseudovectors (tales como velocidad angular o campo magnético) con tales matrices antisimétrica. Es evidente que tales cantidades físicas tendrán n (n-1) / 2 componentes independientes en n dimensiones, lo que coincide con el número de dimensiones para el espacio tridimensional, y es por eso pueden usarse vectores (y más a menudo se utilizan) para representar cantidades tales.
Esta notación es también a menudo mucho más fácil trabajar con, por ejemplo, en geometría epipolar.
De las propiedades generales del producto cruz sigue inmediatamente que
![[\ Mathbf {a}] _ {\ épocas} \, \ mathbf {a} = \ vec {0}](../../images/212/21241.png) y
y ![\ Mathbf {a} ^ {T} \ [\ mathbf {a}] _ {\ épocas} = \ vec {0}](../../images/212/21242.png)
y desde hecho de que ![[\ Mathbf {a}] _ {\ épocas}](../../images/212/21243.png) es antisimétrica se deduce que
es antisimétrica se deduce que
La expansión triple producto mencionados arriba (regla bac-taxi) se puede probar fácilmente con esta notación.
La definición anterior de ![[\ Mathbf {a}] _ {\ épocas}](../../images/212/21243.png) significa que hay un mapeo uno a uno entre el conjunto de matrices 3 × 3 skew-simétricas, también denota SO (3), y la operación de tomar el producto cruzado con algún vector
significa que hay un mapeo uno a uno entre el conjunto de matrices 3 × 3 skew-simétricas, también denota SO (3), y la operación de tomar el producto cruzado con algún vector 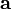 .
.
Notación Índice
El producto cruz, alternativamente, se puede definir en términos de la Levi-Civita tensor 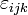
donde los índices 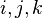 corresponden, como en la sección anterior, a los componentes vectoriales ortogonales.
corresponden, como en la sección anterior, a los componentes vectoriales ortogonales.
Mnemotécnico
La palabra xyzzy se puede utilizar para recordar la definición del producto cruz.
Si
donde:
entonces:
Observe que las segunda y tercera ecuaciones se pueden obtener de la primera simplemente verticalmente girando los subíndices, x → y → z → x. El problema, por supuesto, es cómo recordar la primera ecuación, y dos opciones están disponibles para este propósito: o bien te acuerdas de los pertinentes dos diagonales del esquema de Sarrus (los que contienen i), o recordar la secuencia xyzzy.
Desde la primera diagonal en el esquema de Sarrus es sólo el diagonal principal de la anterior -mentioned 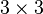 matriz, las tres primeras letras de la palabra xyzzy puede ser muy fácil de recordar.
matriz, las tres primeras letras de la palabra xyzzy puede ser muy fácil de recordar.
Aplicaciones
Geometría computacional
El producto cruzado se puede utilizar para calcular la normal para un triángulo o polígono, una operación que se realiza con frecuencia en gráficos de computadora.
En la geometría computacional de plano , el producto cruzado se utiliza para determinar el signo de la ángulo agudo definido por tres puntos 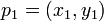 ,
, 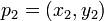 y
y 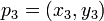 . Se corresponde con la dirección de el producto cruzado de los dos coplanares vectores definidos por los pares de puntos
. Se corresponde con la dirección de el producto cruzado de los dos coplanares vectores definidos por los pares de puntos 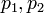 y
y 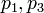 , Es decir, por el signo de la expresión
, Es decir, por el signo de la expresión 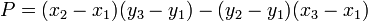 . En el sistema "diestro" coordinar, si el resultado es 0, los puntos están alineados; si es positivo, los tres puntos constituyen un ángulo negativo de rotación alrededor
. En el sistema "diestro" coordinar, si el resultado es 0, los puntos están alineados; si es positivo, los tres puntos constituyen un ángulo negativo de rotación alrededor 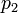 desde
desde 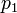 a
a 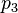 , De lo contrario un ángulo positivo. Desde otro punto de vista, el signo de
, De lo contrario un ángulo positivo. Desde otro punto de vista, el signo de 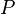 dice si
dice si 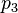 se encuentra a la izquierda oa la derecha de la línea
se encuentra a la izquierda oa la derecha de la línea  .
.
Otro
El producto cruz se produce en la fórmula para el operador vectorial rizo. También se utiliza para describir la Fuerza de Lorentz experimentada por una carga eléctrica se mueve en un campo magnético. Las definiciones de par y momento angular también implican el producto vectorial.
El truco de la reescritura de un producto cruzado en términos de una multiplicación de matrices aparece con frecuencia en epipolar y multi-vista geometría, en particular, cuando se derivan limitaciones coincidentes.
Producto de la Cruz como un producto exterior
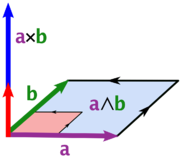
El producto vectorial se puede ver en términos de la producto exterior. Esta visión permite una interpretación geométrica natural del producto cruz. En exterior cálculo el exterior del producto (o producto cuña) de dos vectores es un bivector. A bivector es un elemento plano orientado, de la misma manera que un vector es un elemento de línea orientada. Dados dos vectores A y B, se puede ver el bivector un ∧ b como el paralelogramo orientado atravesado por a y b. El producto cruz entonces se obtiene tomando la Hodge dual del bivector un ∧ b, identificando 2-vectores con vectores:
Esto puede ser considerado como el elemento multidimensional orientado "perpendicular" al bivector. Sólo en tres dimensiones es el resultado de un elemento orientado línea - un vector - mientras que, por ejemplo, en 4 dimensiones del Hodge dual de un bivector es bidimensional - otro elemento plano orientado. Por lo tanto, en tres dimensiones sólo es el producto cruzado de a y b el vector dual a la bivector un ∧ b: es perpendicular a la bivector, con orientación depende de la lateralidad del sistema de coordenadas, y tiene la misma magnitud con respecto a la normal de la unidad vector como un ∧ b tiene respecto a la unidad bivector; precisamente las propiedades descritas anteriormente.
Producto de la Cruz y la lateralidad
Cuando cantidades medibles involucran productos cruzados, la imparcialidad de los sistemas de coordenadas utilizados no puede ser arbitraria. Sin embargo, cuando las leyes de la física se escriben como ecuaciones, debería ser posible hacer una elección arbitraria del sistema de coordenadas (incluyendo uso de las manos). Para evitar problemas, se debe tener cuidado de no escribir una ecuación en la que las dos partes no se comportan igual en todas las transformaciones que deben tenerse en cuenta. Por ejemplo, si un lado de la ecuación es un producto vectorial de dos vectores, hay que tener en cuenta que cuando la imparcialidad del sistema de coordenadas no está fijado a priori, el resultado no es un (verdadero) vectores sino una pseudovector. Por lo tanto, para la consistencia, el otro lado debe ser también un pseudovector.
Más en general, el resultado de un producto cruzado puede ser un vector o una pseudovector, dependiendo del tipo de sus operandos (vectores o pseudovectors). Es decir, vectores y pseudovectors están interrelacionados en las siguientes formas menores de la aplicación del producto cruz:
- vector x = vector pseudovector
- vector × pseudovector = vector
- pseudovector × pseudovector = pseudovector
Debido a que el producto cruzado puede ser también un (true) vector, puede que no cambie de dirección con una transformación de la imagen del espejo. Esto ocurre, de acuerdo con las relaciones anteriores, si uno de los operandos es un (true) vector y el otro es un pseudovector (por ejemplo, el producto cruzado de dos vectores). Por ejemplo, una vector producto triple que involucra a tres (verdaderos) vectores es un (verdadero) vectores.
Un enfoque imparcialidad libre es posible utilizando álgebra exterior.
Dimensiones superiores
Hay varias maneras de generalizar el producto cruzado de las dimensiones superiores.
En el contexto de álgebra multilineal, es posible definir un producto cruzado generalizada en términos de paridad de tal manera que el producto cruzado generalizada entre dos vectores de dimensión n es una sesgar-simétrica tensores de rango N -2.
Utilizando octoniones
Un producto cruz por vectores 7-dimensionales se puede obtener de la misma manera mediante el uso de la octoniones lugar de los cuaterniones. La inexistencia de este tipo de productos cruzados de dos vectores en las otras dimensiones está relacionado con el resultado de que el único álgebras de división normados son los que tienen la dimensión 1, 2, 4 y 8.
Producto de la cuña
En la dimensión general, no hay análogo directo del producto cruz binario. Sin embargo, existe la producto de cuña, que tiene propiedades similares, excepto que el producto de cuña de dos vectores es ahora una 2-vector en lugar de un vector de corriente. Como se mencionó anteriormente, el producto cruzado puede ser interpretado como el producto de cuña en tres dimensiones después de usar Hodge dualidad para identificar 2-vectores con vectores.
También se puede construir un análogo ary n del producto cruz en I n 1 dada por
Esta fórmula es idéntica en estructura a la fórmula determinante para el producto transversal normal en R 3, excepto que la fila de vectores de la base es la última fila en el determinante más que la primera. La razón de esto es asegurar que los vectores ordenados (v 1, ..., v n, Λ (v 1, ..., v n)) tienen un positivo orientación con respecto a (e 1, ..., e n +1). Si n es par, esta modificación deja el valor sin cambios, por lo que este convenio está de acuerdo con la definición normal del producto binario. En el caso de que n es impar, sin embargo, la distinción debe mantenerse. Esta forma n -ario goza de muchas de las mismas propiedades que el producto vectorial: es alterna y lineal en sus argumentos, es perpendicular a cada argumento, y su magnitud da la hipervolumen de la región limitada por los argumentos. Y al igual que el producto vectorial, que se puede definir en una coordenada de manera independiente como el dual de Hodge del producto exterior de los argumentos.
El producto cuña y producto escalar se pueden combinar para formar el Producto Clifford.
Historia
En 1773, Joseph Louis Lagrange introdujo la forma componente tanto el punto y productos cruzados con el fin de estudiar el tetraedro en tres dimensiones. En 1843 el físico matemático irlandés Sir William Rowan Hamilton introdujo el producto de cuaterniones, y con ella los términos "vector" y "escalar". Dadas dos cuaterniones [0, u] y [0, v], donde u y v son vectores en R3, su producto cuaternión pueden resumirse como [- u · v, u × v]. James Clerk Maxwell utiliza herramientas de cuaterniones de Hamilton para desarrollar sus famosas ecuaciones del electromagnetismo , y por esta y otras razones cuaterniones durante un tiempo eran una parte esencial de la educación física.
Sin embargo, Oliver Heaviside en Inglaterra y Josiah Willard Gibbs en Connecticut consideró que los métodos de cuaterniones eran demasiado engorroso, requiriendo a menudo la parte escalar o vectorial de un resultado que se extraiga. Por lo tanto, de unos cuarenta años después de que el producto de cuaterniones, la producto escalar y producto vectorial se introdujeron - a la oposición climatizada. Pivotal a (eventual) de aceptación fue la eficiencia del nuevo enfoque, permitiendo Heaviside para reducir las ecuaciones del electromagnetismo de originales 20 a los cuatro comúnmente visto hoy de Maxwell.
En gran medida independiente de este desarrollo, y en gran medida no apreciado en el momento, Hermann Grassmann creado un álgebra geométrica no atado a dimensionar dos o tres, con la producto exterior juega un papel central. William Kingdon Clifford combina las álgebras de Hamilton y Grassmann para producir Clifford álgebra, donde en el caso de tres dimensiones vectores de la bivector producido a partir de dos vectores dualizes a un vector, reproduciendo así el producto vectorial.
La notación cruz, que comenzó con Gibbs, inspiró el nombre de "producto cruzado". Originalmente apareciendo en las notas publicadas en privado para sus estudiantes en 1881 como elementos de análisis vectorial, la notación de Gibbs - y el nombre - más tarde llegó a un público más amplio a través Análisis vectorial (Gibbs / Wilson), un libro de texto por un ex alumno. Edwin Bidwell Wilson reorganizó el material de las conferencias de Gibbs, junto con material de las publicaciones de Heaviside, Föpps, y Hamilton. Dividió el análisis vectorial en tres partes:
- "En primer lugar, lo que se refiere a la suma y las escalares y vectoriales productos de vectores. En segundo lugar, lo que se refiere al cálculo diferencial e integral en sus relaciones con las funciones escalares y vectoriales. En tercer lugar, la que contiene la teoría de la función vectorial lineal."
Dos tipos principales de multiplicaciones vector se definieron, y fueron llamados de la siguiente manera:
- El escalar o producto directo, escalar de dos vectores
- La inclinación, vector, producto o cruz de dos vectores
Varios tipos de También se examinaron los productos triples y productos de más de tres vectores. La expansión triple producto mencionado anteriormente también se incluyó.


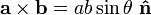
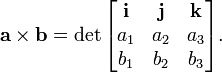
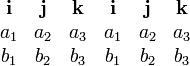
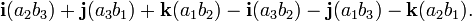
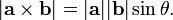
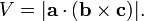
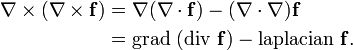
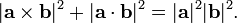
![\ Mathbf {a} \ times \ mathbf {b} = [\ mathbf {a}] _ {\ veces} \ mathbf {b} = \ begin {bmatrix} \, 0 & \ - a_3 & \, \, a_2 \\ \, \, a_3 y 0 & \ - a_1 \\ - a_2 & \, \, a_1 & \, 0 \ end {bmatrix} \ begin {} bmatrix b_1 \\ \\ b_2 b_3 \ end {bmatrix}](../../images/212/21236.png)
![\ Mathbf {b} \ times \ mathbf {a} = [\ mathbf {a}] ^ T _ {\ veces} \ mathbf {b} = \ begin {bmatrix} \, 0 & \, \, a_3 & \ - a_2 \ \ -a_3 y 0 & \, \, a_1 \\\, \, a_2 & \ - a_1 & \, 0 \ end {bmatrix} \ begin {} bmatrix b_1 \\ \\ b_2 b_3 \ end {bmatrix}](../../images/212/21237.png)
![[\ Mathbf {a}] _ {\ veces} \ stackrel {\ rm def} {} = \ begin {bmatrix} \, \, 0 & \ - a_3 & \, \, \, a_2 \\\, \, \ , a_3 y 0 & \ - a_1 \\\ - a_2 & \, \, a_1 & \, \, 0 \ end {bmatrix}.](../../images/212/21238.png)
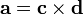
![[\ Mathbf {a}] _ {\ veces} = (\ mathbf {c} \ mathbf {d} ^ T) ^ T - \ mathbf {c} \ mathbf {d} ^ T.](../../images/212/21240.png)
![\ Mathbf {b} ^ {T} \ [\ mathbf {a}] _ {\ épocas} \, \ mathbf {b} = 0.](../../images/212/21244.png)