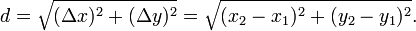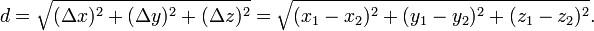Contenido Checked

Distancia

Temas relacionados: Matemáticas

Antecedentes

SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. Apadrina un niño para hacer una diferencia real.

La distancia es una descripción numérica de cuán lejos están los objetos. En la física o la discusión cotidiana, la distancia puede referirse a una longitud física, un período de tiempo, o una estimación basada en otros criterios (por ejemplo, "dos condados más"). En matemáticas , la distancia debe cumplir con criterios más rigurosos.

En la mayoría de los casos hay simetría y "distancia de A a B" es intercambiable con "distancia entre B y A".

Matemáticas

Geometría

En geometría neutral, la distancia mínima entre dos puntos es la longitud de la segmento de línea entre ellos.

En la geometría analítica , la distancia entre dos puntos del plano xy se puede encontrar utilizando la fórmula de distancia. La distancia entre (x 1, y 1) y (x 2, y 2) está dada por

d = \ sqrt {(\ Delta x) ^ 2 + (\ Delta y) ^ 2} = \ sqrt {(x_2-x_1) ^ 2 + (y_2-y_1) ^ 2}. \,

Puntos de la misma manera, dadas (x 1, y 1, z 1) y (x 2, y 2, z 2) en tres espacios , la distancia entre ellos es

d = \ sqrt {(\ Delta x) ^ 2 + (\ Delta y) ^ 2 + (\ Delta z) ^ 2} = \ sqrt {(x_1-x_2) ^ 2 + (y_1-y_2) ^ 2 + ( z_1-Z_2) ^ 2}.

Que es fácilmente demostrada mediante la construcción de un triángulo rectángulo con una pierna en el hipotenusa de otra (con la otra pierna ortogonal al plano que contiene la primera triángulo) y aplicando el teorema de Pitágoras .

En el estudio de geometrías complicadas, llamamos a este tipo (el más común) de distancia Distancia euclídea, ya que se deriva del teorema de Pitágoras , que no se sostiene en Geometrías no euclidianas. Esta distancia fórmula también se puede ampliar en el fórmula longitud de arco.

Distancia en el espacio euclidiano

En el espacio euclídeo R n, la distancia entre dos puntos es generalmente dada por la Distancia euclídea (distancia 2-norma). Otras distancias, sobre la base de otra las normas, a veces se utilizan en su lugar.

Para un punto (x 1, x 2, ..., x n) y un punto (y 1, y 2, ..., y n), la distancia de Minkowski de orden p (distancia p-norma) se define como :

Distancia 1-norma 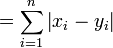= \ Sum_ {i = 1} ^ n \ left | x_i - y_i \ right |
Distancia 2-norma 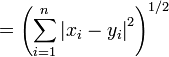= \ Left (\ sum_ {i = 1} ^ n \ left | x_i - y_i \ right | ^ 2 \ right) ^ {1/2}
distancia-norma p 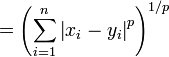= \ Left (\ sum_ {i = 1} ^ n \ left | x_i - y_i \ right | ^ p \ right) ^ {1 / p}
distancia norma infinito 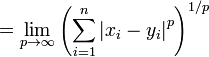= \ {Lim_ p \ to \ infty} \ left (\ sum_ {i = 1} ^ n \ left | x_i - y_i \ right | ^ p \ right) ^ {1 / p}
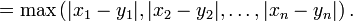= \ Max \ left (| x 1 - y_1 |, | x_2 - y_2 |, \ ldots, | x_n - y_n | \ right).

p no tiene que ser un número entero, pero no puede ser inferior a 1, porque de lo contrario la desigualdad del triángulo no se sostiene.

La distancia 2-norma es la Distancia euclidiana, una generalización del teorema de Pitágoras a más de dos coordina. Es lo que se obtendría si la distancia entre dos puntos se midieron con una gobernante: la idea "intuitiva" de distancia.

La distancia 1-norma es más colorido llama la norma taxi o Manhattan distancia, ya que es la distancia que un coche sería conducir en una ciudad diseñada en bloques cuadrados (si no hay calles de un solo sentido).

La distancia norma infinito también se llama Distancia Chebyshev. En 2D representa la distancia reyes tienen que viajar entre dos plazas en un tablero de ajedrez.

El p-norma rara vez se utiliza para valores de p distintos de 1, 2, y el infinito, pero ver súper elipse.

En el espacio físico de la distancia euclidiana es de una forma la más natural, porque en este caso la longitud de una cuerpo rígido no cambia con rotación.

Caso general

En matemáticas , en particular, la geometría , una función de distancia en un determinado conjunto M es una función de d: M × M → R, donde R denota el conjunto de números reales , que satisface las siguientes condiciones:

  • d (x, y) ≥ 0, y d (x, y) = 0 si y sólo si x = y. (La distancia es positiva entre dos puntos diferentes, y es cero, precisamente, de un punto a sí mismo.)
  • Es simétrica: d (x, y) = d (y, x). (La distancia entre x e y es la misma en cualquier dirección.)
  • Satisface el desigualdad triangular: d (x, z) ≤ d (x, y) + d (y, z). (La distancia entre dos puntos es la distancia más corta a lo largo de cualquier camino).

Tal función de distancia se conoce como una métrica. Junto con el conjunto, lo compensa con un espacio métrico.

Por ejemplo, la definición usual de distancia entre dos números reales x e y es: d (x, y) = | x - y |. Esta definición satisface las tres condiciones anteriores, y se corresponde con el estándar de la topología de la recta real. Pero la distancia en un conjunto dado es una opción de definición. Otra opción posible es definir: d (x, y) = 0 si x = y, y 1 en caso contrario. Esto también define una métrica, pero da una topología completamente diferente, el " topología discreta ", con estos números definición no puede ser arbitrariamente cerca.

Distancias entre series y entre un punto y un conjunto

d (A, B)> d (A, C) + d (C, B)

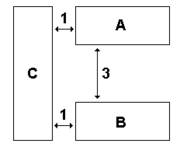
Varias definiciones distancia son posibles entre objetos. Por ejemplo, entre los cuerpos celestes no hay que confundir la distancia de superficie a superficie y la distancia de centro a centro. Si el primero es mucho menor que el segundo, como para una LEO, la primera tiende a ser citado (altitud), de lo contrario, por ejemplo, para la distancia Tierra-Luna, el último.

Hay dos definiciones comunes para la distancia entre dos no vacíos subconjuntos de un conjunto dado:

  • Una versión de la distancia entre dos conjuntos no vacíos es la ínfimo de las distancias entre dos de sus puntos, que es el significado de todos los días de la palabra. Este es un simétrica prametric. En una colección de conjuntos de los cuales algún toque o se superponen entre sí, no es "separación", ya que la distancia entre dos conjuntos diferentes, pero se tocan o solapan es cero. Además, no es hemimetric, es decir, el desigualdad del triángulo no se sostiene, excepto en casos especiales. Por lo tanto, sólo en casos especiales esta distancia hace que una colección de conjuntos un espacio métrico.
  • La Hausdorff distancia es el mayor de dos valores, uno de ellos el supremum, para un punto que varía más de un conjunto, de la ínfimo, por un segundo punto que van sobre el otro conjunto, de la distancia entre los puntos, y el otro valor que se está igualmente definido pero con los papeles de los dos conjuntos intercambiadas. Esta distancia hace que el conjunto de no vacíos compactos subconjuntos de un espacio métrico sí mismo una espacio métrico.

La Módulo: Metric_space ( hablar · · hist · Enlaces · subpáginas · pruebas - los resultados) es el ínfimo de las distancias entre el punto y los del conjunto. Esto corresponde a la distancia, de acuerdo con el mencionado en primer lugar definición anterior de la distancia entre los conjuntos, desde el conjunto que contiene sólo este punto al otro conjunto.

En cuanto a esto, la definición de la distancia de Hausdorff se puede simplificar: es el mayor de dos valores, uno de ellos el supremo, por un punto que va más de un conjunto, de la distancia entre el punto y el juego, y el otro valor siendo igualmente definido pero con los papeles de los dos conjuntos intercambiadas.

Distancia-desplazamiento

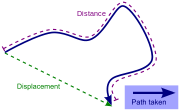
Distancia a lo largo de un camino en comparación con el desplazamiento

La distancia no puede ser negativa . La distancia es una cantidad escalar, que contiene sólo una magnitud, mientras el desplazamiento es un equivalente vector que contiene la cantidad tanto en magnitud como dirección.

La distancia recorrida por un vehículo (a menudo grabada por una odómetro), persona, animal, objeto, etc. debe distinguirse de la distancia del punto inicial al punto final, aunque este último se entiende por ejemplo, la distancia más corta a lo largo de la carretera, porque un desvío podría hacerse, y el punto final incluso puede coincidir con el punto de partida.

Otros "distancias"

  • La distancia de Mahalanobis se utiliza en las estadísticas .
  • Distancia de Hamming se utiliza en teoría de la codificación.
  • Levenshtein distancia
  • Chebyshev distancia
Recuperado de " http://en.wikipedia.org/w/index.php?title=Distance&oldid=202869167 "