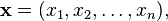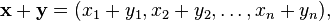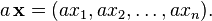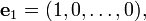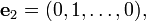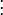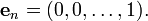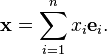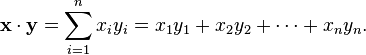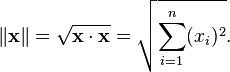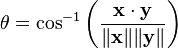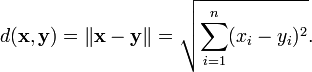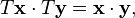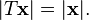Espacio euclidiano
Antecedentes
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Haga clic aquí para obtener más información sobre SOS Children.
Alrededor 300 antes de Cristo , el griego matemático Euclides realizó un estudio de las relaciones entre las distancias y ángulos , por primera vez en un avión (una superficie plana idealizado) y luego en el espacio. Un ejemplo de una relación de este tipo es que la suma de los ángulos de un triángulo es siempre 180 grados. Hoy en día estas relaciones se conocen como de dos y tres dimensional geometría euclidiana .
En la moderna matemática lengua, la distancia y el ángulo pueden generalizarse fácilmente a los espacios 4-dimensionales, 5-dimensionales, e incluso de dimensiones superiores. Un espacio n-dimensional con las nociones de distancia y el ángulo que obedecen a las relaciones euclidianas se llama un espacio euclidiano dimensional n. La mayor parte de este artículo está dedicado al desarrollo de la lengua moderna necesaria para el salto conceptual de dimensiones superiores.
Una propiedad esencial de un espacio euclidiano es su planeidad. Existen otros espacios en la geometría euclidiana que no lo son. Por ejemplo, la superficie de una esfera no lo es; un triángulo en una esfera (convenientemente definido) tendrá ángulos que resumen a algo mayor que 180 grados. De hecho, no es esencialmente sólo un espacio euclidiano de cada dimensión, mientras que hay muchos espacios no euclidianas de cada dimensión. A menudo, estos otros espacios se construyen mediante la deformación sistemáticamente espacio euclidiano.
Resumen intuitivo
Una forma de pensar en el plano euclidiano es como conjunto de señala ciertas relaciones satisfactorias, expresables en términos de distancia y ángulo. Por ejemplo, hay dos operaciones fundamentales en el plano. Uno es traducción, lo que significa un desplazamiento del plano de manera que cada punto se desplaza en la misma dirección y por la misma distancia. El otro es rotación alrededor de un punto fijo en el plano, en el que cada punto en el plano gira alrededor de ese punto fijo a través del mismo ángulo. Uno de los principios básicos de la geometría euclidiana es que dos figuras (es decir, subconjuntos ) del plano deben considerarse equivalentes ( congruentes) si uno puede ser transformado en el otro por una secuencia de traslaciones y rotaciones. (Ver Grupo euclidiana.)
Para hacer todo esto matemáticamente precisa, se debe definir claramente los conceptos de distancia, el ángulo, la traducción y la rotación. La forma habitual de hacer esto, como se realiza en el resto de este artículo, es definir el plano euclidiano como bidimensional verdadero espacio vectorial equipado con un producto interno. Para entonces:
- la vectores en el espacio vectorial corresponden a los puntos del plano euclidiano,
- la adición operación en el espacio vectorial corresponde a la traducción, y
- el producto interno implica nociones de ángulo y distancia, que pueden ser utilizados para definir la rotación.
Una vez que el plano euclidiano se ha descrito en este idioma, en realidad es una simple cuestión de extender su concepto a dimensiones arbitrarias. En su mayor parte, el vocabulario, las fórmulas y cálculos no se hacen más difícil por la presencia de más dimensiones. (Sin embargo, las rotaciones son más sutiles en grandes dimensiones, y la visualización de espacios de alta dimensión sigue siendo difícil, incluso para los matemáticos experimentados.)
Una arruga final es que el espacio euclidiano no es técnicamente un espacio vectorial, sino más bien una espacio afín, en el que un espacio vectorial actúa. Intuitivamente, la distinción sólo dice que no hay elección canónica de donde el origen debe ir en el espacio, ya que se puede traducir en cualquier lugar. En este artículo, este tecnicismo es ignorado en gran medida.
Coordinar Bienes espacio
Sea R denota el campo de los números reales . Para cualquier no negativo entero n, el espacio de todos los n - tuplas de números reales forma un espacio vectorial dimensional n más de R, que se denota R n y a veces se llama verdadero espacio de coordenadas. Un elemento de R n se escribe
donde cada x i es un número real. Las operaciones en el espacio vectorial sobre R n se definen por
El espacio vectorial R n viene con una base estándar:
Un vector arbitrario en R n se puede escribir en la forma
R n es el ejemplo prototípico de un verdadero n-dimensional espacio vectorial. De hecho, cada verdadero espacio vectorial n-dimensional V es isomorfo a R n. Este isomorfismo no es canónica, sin embargo. Una selección de isomorfismo es equivalente a la opción de base para V (mirando a la imagen de la base estándar para R n en V). La razón para trabajar con espacios vectoriales arbitrarios en lugar de R n es que a menudo es preferible trabajar de una manera coordinar libre (es decir, sin la elección de una base preferida).
Estructura euclidiana
Espacio euclidiano es algo más que un verdadero espacio de coordenadas. Para la aplicación de la geometría euclidiana que uno tiene que ser capaz de hablar de las distancias entre puntos y los ángulos entre líneas o vectores. La forma natural de obtener estas cantidades es mediante la introducción y utilizar el producto interior estándar (también conocido como el dot producto) en R n. El producto interno de dos vectores x e y se define por
El resultado es siempre un número real. Además, el producto interno de x con sí mismo es siempre no negativo. Este producto nos permite definir la "longitud" de un vector x como
Esta función de longitud satisface las propiedades requeridas de una norma y se llama la norma euclidiana en I n.
La (no obtuso) ángulo θ (0 ° ≤ θ ≤ 180 °) entre x e y entonces dada por
donde cos -1 es el función arco coseno.
Finalmente, se puede usar la norma para definir una métrica (o función de distancia) en R n por
Esta función se llama la distancia Métrica euclidiana. Puede ser visto como una forma de la teorema de Pitágoras .
Coordinar Bienes espacio junto con esta estructura euclidiana se llama el espacio euclidiano y, a menudo denotado E n. (Muchos autores se refieren a R n como espacio euclidiano, con la estructura euclidiana entendiéndose). La estructura euclidiana hace E n una espacio del producto interior (de hecho, una Espacio de Hilbert), un espacio vectorial normado, y un espacio métrico.
Rotaciones de espacio euclidiano, se definen como conserva la orientación Transformaciones lineales T que preservan ángulos y longitudes:
En el lenguaje de las matrices , las rotaciones son matrices ortogonales especiales.
Topología del espacio euclidiano
Dado que el espacio euclidiano es una espacio métrico también es una espacio topológico con lo natural topología inducida por la métrica. La topología métrica sobre E n se llama la topología euclidiana. Un conjunto es abierto en la topología euclidiana si y sólo si contiene una bola abierta en torno a cada uno de sus puntos. La topología euclidiana resulta ser equivalente a la topología producto en R n considerado como un producto de n copias de la recta real R (con su topología estándar).
Un resultado importante de la topología de R n, que está lejos de ser superficial, es Brouwer de invariancia del dominio. Cualquier subconjunto de R n (con su topología del subespacio) es homeomorfo a otro subconjunto abierto de R n es en sí mismo abierto. Una consecuencia inmediata de esto es que la I m no es homeomorfo a R n si m ≠ n - una intuitivamente "obvio" número que es, sin embargo, difícil de probar.
Las generalizaciones
En las matemáticas modernas, espacios euclídeos forman los prototipos para otros más complicados objetos geométricos. Por ejemplo, una múltiple liso es una Hausdorff espacio topológico que es localmente difeomorfa a espacio euclidiano. Difeomorfismo no respeta la distancia y el ángulo, por lo que estos conceptos claves de la geometría euclidiana se pierden en una variedad diferenciable. Sin embargo, si se prescribe, además, un producto interior suavemente variable en el colector de espacios tangentes, entonces el resultado es lo que se denomina Variedad de Riemann. Dicho de otra manera, una variedad de Riemann es un espacio construido por deformación y remendar juntos espacios euclídeos. Dicho espacio cuenta con nociones de distancia y el ángulo, pero se comportan de una curvada manera, no euclidiana. La variedad de Riemann más simple, que consiste en R n con un producto interno constante, es esencialmente idéntica a euclidiana n-espacio en sí.
Si uno altera un espacio euclidiano de modo que su producto interno se vuelve negativo en una o más direcciones, entonces el resultado es una espacio pseudo-euclidiana. Múltiples lisos construidos a partir de tales espacios se llaman colectores pseudo-riemanniana. Tal vez su aplicación más famosa es la teoría de la relatividad , donde vacía espacio-tiempo sin cuestión está representada por el espacio pseudo-euclidiana plana llamada El espacio de Minkowski, espaciotiempos con la materia en ellos forman otros colectores de pseudo-Riemann, y la gravedad corresponde a la curvatura de una variedad tal.
Nuestro universo, estando sujeto a la relatividad, no es euclidiana. Esto se convierte en significativo en consideraciones teóricas de la astronomía y la cosmología , y también en algunos problemas prácticos como de posicionamiento global y avión navegación. Sin embargo, un modelo euclidiano del universo todavía se puede utilizar para resolver muchos otros problemas prácticos con suficiente precisión.