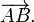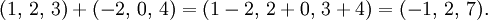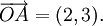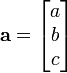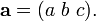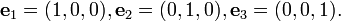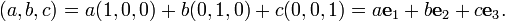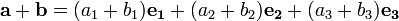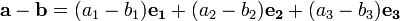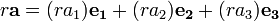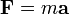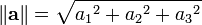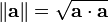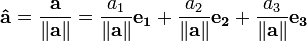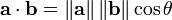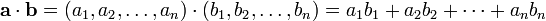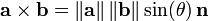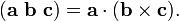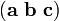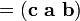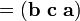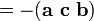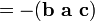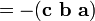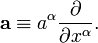Vector

Un vector que va de A a B.

Un vector espacial, o simplemente vector, es un objeto geométrico que tiene tanto una magnitud y una dirección. Un vector se representa con frecuencia por una segmento de línea que une el punto A inicial con el punto B y denotado terminales

La magnitud es la longitud del segmento y la dirección caracteriza el desplazamiento de B respecto a A: cuánto se debe mover el punto A a "llevar" hasta el punto B.

Muchos operaciones algebraicas en los números reales tienen estrechos análogos para los vectores. Los vectores pueden ser añadidos , restados , multiplicado por un número, y da la vuelta alrededor de modo que la dirección se invierte. Estas operaciones obedecen las leyes algebraicas familiares: conmutatividad , asociatividad , distributividad. La suma de dos vectores con el mismo punto inicial se puede encontrar geométricamente usando el ley del paralelogramo. La multiplicación por un número positivo, comúnmente llamado un escalar en este contexto, que equivale a cambiar la magnitud del vector, es decir, estiramiento o compresión mientras que mantiene su dirección; la multiplicación por -1 preserva la magnitud del vector pero invierte su dirección.

Coordenadas cartesianas proporcionan una forma sistemática de describir vectores y operaciones con ellos. Un vector se convierte en un triple de los números reales, sus componentes. La adición de vectores y multiplicación de un vector por un escalar se hace simplemente componente por componente, consulte coordinar vector.

Vectores juegan un papel importante en la física : la velocidad y la aceleración de un objeto en movimiento y las fuerzas que actúan sobre un cuerpo son todos descrito por vectores. Muchas otras cantidades físicas pueden ser útilmente considerados como vectores. Uno tiene que tener en cuenta, sin embargo, que los componentes de un vector físico dependen de la sistema utilizado para describir de coordenadas. Otros objetos en vectores que describen como cantidades físicas y transforman de una manera similar bajo cambios del sistema de coordenadas incluyen pseudovectors y tensores.

Visión de conjunto

De manera informal, un vector es una cantidad caracterizado por una magnitud (en matemáticas un número, en la física de un número de veces de una unidad) y una dirección, a menudo representan gráficamente por una flecha. A veces, se habla de vectores encuadernados o fijos, que son vectores cuyo punto inicial es el origen. Esto está en contraste con vectores libres, que son vectores cuyo punto inicial no es necesariamente el origen.

El uso en la física y la ingeniería

Los vectores son fundamentales en las ciencias físicas. Pueden ser utilizados para representar cualquier cantidad que tiene una magnitud y dirección, tales como la velocidad , la magnitud de los cuales es velocidad. Por ejemplo, la velocidad de 5 metros por segundo hacia arriba podían ser representados por el vector (0,5). Otra cantidad representada por un vector es la fuerza , ya que tiene una magnitud y dirección. Los vectores también describen muchas otras cantidades físicas, tales como desplazamiento, aceleración , eléctrica y campos magnéticos, impulso y momento angular .

Vectores en el espacio cartesiano

En coordenadas cartesianas , un vector puede representarse mediante la identificación de las coordenadas de su punto inicial y terminal. Por ejemplo, los puntos A = (1,0,0) y B = (0,1,0) en el espacio libre de determinar el vector 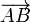señalando desde el punto x = 1 en el eje x y al punto = 1 en el eje y.

Normalmente, en coordenadas cartesianas, se considera vectores principalmente ligados. Un vector de la envolvente está determinada por las coordenadas del punto terminal, su punto inicial que tiene siempre las coordenadas del origen O = (0,0,0). Así, el vector de la envolvente representada por (1,0,0) es un vector de unidad de longitud que apunta desde el origen hasta el eje x positivo.

La representación de coordenadas de vectores permite que las características algebraicas de vectores que se expresen de forma numérica conveniente. Por ejemplo, la suma de los vectores (1,2,3) y (-2,0,4) es el vector

Vectores y vectores afines euclidiana

En los ajustes geométricos y físicos, a veces es posible asociar, de una manera natural, una longitud a los vectores, así como la noción de un ángulo entre dos vectores. Cuando se define la longitud de los vectores, es posible definir también un producto de punto - un producto escalar de valor de dos vectores - que da una caracterización algebraica conveniente de la longitud y el ángulo. En tres dimensiones, es posible además definir un producto cruzado que suministra una caracterización algebraica de área.

Sin embargo, no siempre es posible o deseable para definir la longitud de un vector de una manera natural. Este tipo más general de vector espacial es el tema de los espacios vectoriales (por vectores encuadernadas) y espacios afines (por vectores libres).

Las generalizaciones

En las clases más generales de los sistemas, la rotación de un vector (y también de coordinar tensores) se pueden generalizar y categorizar a admitir una caracterización análoga por su covarianza y contravarianza bajo cambios de coordenadas.

En las matemáticas , un vector se considera más de una representación de una cantidad física. En general, un vector es cualquier elemento de un espacio vectorial sobre algunos campo. Los vectores espaciales de este artículo son un caso muy especial de esta definición general (no son simplemente cualquier elemento de R ^d en d dimensiones), que incluye una variedad de objetos matemáticos ( álgebras, la conjunto de todas las funciones de un dado dominio a un lineal dada gama, y transformaciones lineales). Tenga en cuenta que bajo esta definición, un tensor es un vector especial.

Representación de un vector

Los vectores se denominan generalmente en negrita, como una. Otros convenios incluyen 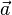o una, especialmente en escritura a mano. Alternativamente, algunos utilizan un tilde (~) o un subrayado ondulado dibujado debajo del símbolo, que es una convención para indicar negrita.

Los vectores son generalmente muestran en los gráficos u otros diagramas como flechas, como se ilustra a continuación:

Aquí el punto A se llama el punto inicial, cola, o base; punto B se llama la cabeza, la punta o extremo. La longitud de la flecha representa la magnitud del vector, mientras que la dirección en la que los puntos de flecha representa la dirección del vector.

En la figura anterior, la flecha también se puede escribir como 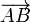o AB.

En un diagrama de dos dimensiones, a veces un vector perpendicular al plano del diagrama se desea. Estos vectores se muestran comúnmente como pequeños círculos. Un círculo con un punto en su centro indica un vector que apunta hacia fuera de la parte frontal del diagrama, hacia el espectador. Un círculo con una cruz inscrita en él indica un vector que apunta en y detrás del diagrama. Estos pueden ser considerados como de ver la una punta flecha frente en y ver las aspas de una flecha de la parte posterior.

Un vector en el plano cartesiano, con punto final (2,3). El vector en sí se identifica con su punto final.

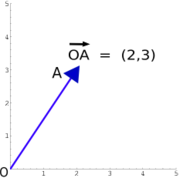
Con el fin de calcular con vectores, la representación gráfica puede ser demasiado engorroso. Vectores en un espacio euclídeo de dimensión n n pueden ser representados en un sistema de coordenadas cartesianas . El punto final de un vector puede ser identificado con una lista de n números reales, a veces llamado una vector fila o vector columna. Como un ejemplo en dos dimensiones (véase la imagen), el vector desde el origen O = (0,0) hasta el punto A = (2,3) es simplemente escribe como

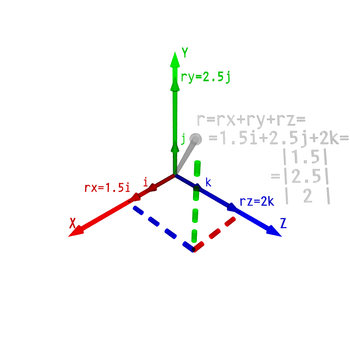
En tres espacio euclidiano tridimensional (o R ^3), los vectores se identifican con triples de números correspondientes a las coordenadas cartesianas del punto final (a, b, c). Estos números son a menudo dispuestos en un vector de columna o fila vector, particularmente cuando se trata de matrices , como sigue:

Otra forma de expresar un vector en tres dimensiones es introducir las tres coordenadas vectores básicos, a veces referido como vectores unitarios:

Estos tienen la interpretación intuitiva como vectores de la unidad de longitud que destacan los, Y y eje z x, respectivamente. En términos de estos, cualquier vector en R ³ se puede expresar en la forma:

Nota: En las clases de introducción a la física, estos tres vectores especiales están a menudo en lugar denotan i, j, k (o 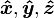cuando en coordenadas cartesianas ), pero estos enfrentamientos con la notación notación índice y el convención sumatoria de uso común en las matemáticas superiores de nivel, la física y la ingeniería. En este artículo se va a optar por utilizar e _1, e _2, e _3.

El uso de vectores unitarios cartesianos 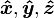como un base en el que representar un vector, no es obligatoria. Los vectores también pueden expresarse en términos de vectores unitarios cilíndricos 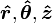o esféricas vectores unitarios 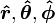. Las dos últimas opciones son más convenientes para la solución de problemas que poseen simetría esférica o cilíndrica, respectivamente.

La suma y la multiplicación escalar

Igualdad vectorial

Dos vectores se dice que son iguales si tienen la misma magnitud y dirección. Sin embargo, si estamos hablando de vectores gratis, luego dos vectores libres son iguales si tienen el mismo punto base y el punto final.

Por ejemplo, el vector e ₁ + 2 + 3 e ₂ e ₃ con el punto base (1,0,0) y el vector e ₁ e 2 ₂ 3 ₃ e con el punto base (0,1,0) son diferentes vectores gratis, pero la misma (desplazamiento) del vector.

Además Vector y resta

Vamos a = a ₁ e ₁ + a ₂ e ₂ + ₃ e ₃ y b = b ₁ e ₁ + b ₂ e ₂ + b ₃ e _3, donde e _1, e _2, e ₃ son vectores unitarios ortogonales (Nota : sólo tienen que ser linealmente independientes, es decir, no en paralelo y no en el mismo plano, para que se apliquen estas reglas de suma y resta algebraicas)

La suma de a y b es:

La adición puede ser representada gráficamente mediante la colocación del inicio de la flecha b en la punta de la flecha A, y luego dibujando una flecha desde el inicio de la A a la punta de b. La nueva flecha dibujada representa el vector a + b, como se ilustra a continuación:

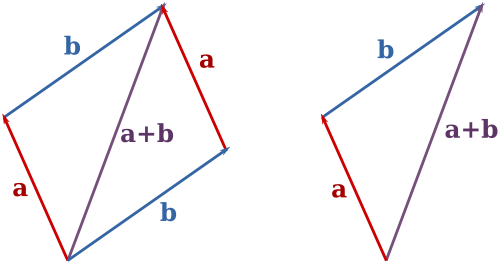
Este método, además a veces se llama la regla del paralelogramo porque ayb formar los lados de un paralelogramo y a + b es una de las diagonales. Si a y b son vectores libres, entonces la adición está definido sólo si A y B tienen el mismo punto de base, que luego también ser el punto de base de a + b. Se puede comprobar geométricamente que a + b = b + a y (a + b) + c = a + (b + c).

La diferencia de A y B es:

La resta de dos vectores puede ser geométricamente definida de la siguiente manera: para restar b de una, colocar los extremos de A y B en el mismo punto, y luego dibujar una flecha desde la punta de b a la punta de una. Eso flecha representa el vector a - b, como se ilustra a continuación:

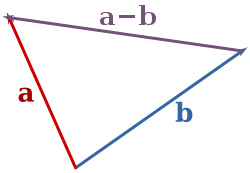
Si a y b son vectores libres, entonces la resta sólo se define si comparten el mismo punto de base que a su vez también se convertirá en el punto base de su diferencia. Esta operación se merece el nombre de "sustracción" porque (a - b) + b = a.

Multiplicación escalar

Un vector también puede ser multiplicado, o re- escala, por un número real r. En el contexto de los vectores espaciales, estos números reales son a menudo llamados escalares (de escala) para distinguirlos de los vectores. La operación de multiplicar un vector por un escalar se llama multiplicación escalar. El vector resultante es:

Multiplicación escalar de un vector por un factor de 3 se extiende a cabo el vector.

Intuitivamente, la multiplicación por un escalar r estira un vector a cabo por un factor de r. Geométricamente, esto puede ser visualizado (al menos en el caso cuando r es un número entero) como la colocación de copias r del vector en una línea donde el punto final de un vector es el punto inicial de la siguiente vector.

Si r es negativa, entonces el vector cambia de dirección: se voltea alrededor de un ángulo de 180 °. Dos ejemplos (r = -1 y r = 2) se dan a continuación:

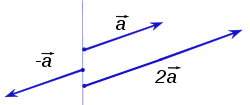
Multiplicación escalar es distributiva sobre la suma de vectores en el sentido siguiente: r (a + b) = r b para todos los vectores a y b r a + y todos los escalares r. También se puede demostrar que a - b = a + (-1) b.

El conjunto de todos los vectores geométricos, junto con las operaciones de suma de vectores y multiplicación escalar, satisface todos los axiomas de un espacio vectorial . Del mismo modo, el conjunto de todos los vectores unidos con un punto de base común forma un espacio vectorial. Aquí es donde se originó el término "espacio vectorial".

En la física, escalares también pueden tener una unidad de medida asociada con ellos. Por ejemplo, la segunda ley de Newton es

donde F tiene unidades de fuerza, una tiene unidades de aceleración, y el escalar m tiene unidades de masa. En una posible interpretación física de el diagrama anterior, la escala de aceleración es, por ejemplo, 2 m / s ^2: cm, y que la fuerza de 5 N: cm. Así, una relación de escala de 2,5 kg: 1 se utiliza para la masa. Del mismo modo, si el desplazamiento tiene una escala de 1: 1000 y la velocidad de 0,2 cm: 1 m / s, o equivalente, 2 ms: 1, una relación de escala de 0,5: s se usa para el tiempo.

La longitud y el producto escalar

Longitud de un vector

La longitud o magnitud o norma del vector a se denota por || a || o, menos comúnmente, | a |, que no se debe confundir con el valor absoluto (una "norma" escalar).

La longitud del vector a = a ₁ e ₁ + a ₂ e ₂ + a ₃ e ₃ en una de tres dimensiones espacio euclidiano , donde E _1, E _2, E ₃ son vectores unitarios ortogonales, se puede calcular con la Norma euclidiana

que es una consecuencia de la teorema de Pitágoras ya que la base de vectores e _1, e _2, e ₃ son vectores unitarios ortogonales.

Esto pasa a ser igual a la raíz cuadrada de la dot producto del vector por sí mismo:

Longitud del vector y las unidades

Si un vector es en sí mismo espacial, la longitud de la flecha depende de una sin dimensiones escala. Si se representa, por ejemplo una fuerza, la "escala" es de física dimensión de longitud / fuerza. Por lo tanto no es típicamente la consistencia en la escala entre cantidades de la misma dimensión, pero por lo demás escala proporciones pueden variar; Por ejemplo, si "1 newton" y "5 m" están representados con una flecha de 2 cm, las escalas son 1: 250 y 1 m: 50 N, respectivamente. Longitud igual de vectores de diferente dimensión no tiene ningún significado particular, a menos que haya alguna constante de proporcionalidad inherente al sistema que el diagrama representa. También longitud de un vector unidad (de dimensión longitud, no la longitud / fuerza, etc.) no ha coordinar invariante del sistema importancia.

Vector unitario

Un vector unitario es cualquier vector con una longitud de uno; geométricamente, indica una dirección, pero no magnitud. Si usted tiene un vector de longitud arbitraria, puede dividirlo por su longitud para crear un vector unitario. Esto se conoce como la normalización de un vector. Un vector unitario se indica a menudo con un sombrero como en una.

Para normalizar un vector a = [a _1, a _2, a _3], escalar el vector por el recíproco de su longitud || a ||. Esto es:

Vector Null

El vector null (o cero vector) es el vector con longitud cero. Escrito en coordenadas, el vector es (0,0,0), y comúnmente se denota 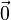O 0, o simplemente 0. A diferencia de cualquier otro vector, que no tiene una dirección, y no se puede normalizar (es decir, no hay vector unitario que es un múltiplo del vector nulo). La suma del vector nulo con cualquier vector a es un (es decir, 0 + a = a).

Producto escalar

Artículo principal: Producto escalar

El producto escalar de dos vectores ayb (a veces llamado el producto interno, o, ya que su resultado es un escalar, el producto escalar) se denota por un ∙ b y se define como:

donde || a || y || b || denota el norma (o longitud) de A y B, y θ es la medida de la ángulo entre A y B (véase la función trigonométrica para una explicación de coseno). Geométricamente, esto significa que a y b se dibujan con un punto de inicio común y luego la longitud de una se multiplica por la longitud de dicho componente de b que apunta en la misma dirección que a.

El producto escalar también puede ser definido como la suma de los productos de los componentes de cada vector:

donde a y b son vectores de n dimensiones; a _1, a _2, ..., a _n son coordenadas de a; y b _1, b _2, ..., b _n son coordenadas de b.

Esta operación suele ser útil en la física ; por ejemplo, el trabajo es el producto escalar de la fuerza y desplazamiento.

Producto de la Cruz

El producto cruzado (también llamado el producto vectorial o producto externo) difiere del producto escalar principalmente en que el resultado del producto vectorial de dos vectores es un vector. Mientras que todo lo que se dijo anteriormente puede generalizarse de una manera directa a más de tres dimensiones, el producto cruzado sólo tiene sentido en tres dimensiones, aunque la siete producto cruzado dimensional es similar en algunos aspectos. El producto cruz, denota a × b, es un vector perpendicular tanto a A y B y se define como:

donde θ es la medida del ángulo entre A y B, y n es un vector unitario perpendicular tanto a y b. El problema con esta definición es que hay dos vectores unitarios perpendiculares tanto a b y a.

Una ilustración del producto cruz.

La base de vectores e _1, e _2, e ₃ se llama diestro, si los tres vectores se sitúan como el pulgar, el dedo índice y el dedo medio (apuntando hacia arriba a partir de la palma) de su mano derecha. Gráficamente el producto cruzado puede ser representado por la figura de la derecha.

El producto una cruz × b se define de manera que a, b, y a × b también se convierte en un sistema de mano derecha (pero tenga en cuenta que A y B no son necesariamente ortogonal). Este es el regla de la mano derecha.

La longitud de un × b puede ser interpretado como el área del paralelogramo que tiene a y b como lados.

Para opciones arbitrarias de orientación espacial (es decir, lo que permite zurdo, así como diestro sistemas de coordenadas) el producto vectorial de dos vectores es un pseudovector en lugar de un vector (véase más adelante).

Triple producto escalar

El triple producto escalar (también llamada la caja o producto triple mixta) no es realmente un nuevo operador, sino una forma de aplicar los otros dos operadores de multiplicación de tres vectores. El producto triple escalar a veces se denota por (a b c) y se define como:

Cuenta con tres usos principales. En primer lugar, el valor absoluto del producto caja es el volumen de la paralelepípedo que tiene bordes que se definen por los tres vectores. En segundo lugar, el producto triple escalar es cero si y sólo si los tres vectores son linealmente dependientes, que puede ser fácilmente demostrado por teniendo en cuenta que, para que los tres vectores para no hacer un volumen, todos ellos deben estar en el mismo plano. En tercer lugar, el producto caja es positivo si y sólo si los tres vectores a, b y c son diestros.

En los componentes (con respecto a una base ortonormal de mano derecha), si los tres vectores son considerados como filas (o columnas, pero en el mismo orden), el producto triple escalar es simplemente el factor determinante de la 3-por-3 matriz teniendo los tres vectores como filas. El triple producto escalar es lineal en las tres entradas y anti-simétrica en el siguiente sentido:

Los componentes del vector

Ilustración de los componentes tangencial y normal de un vector a una superficie.

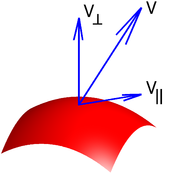
Un componente de un vector es la influencia de ese vector en una dirección dada. Los componentes son ellos mismos vectores.

Un vector se describe a menudo por un número fijo de componentes que sintetizan en este vector única y totalmente. Cuando se usa en este papel, la elección de sus direcciones que constituyen depende del sistema de coordenadas particular que se usa, tales como coordenadas cartesianas , coordenadas esféricas o coordenadas polares . Por ejemplo, el componente axial de un vector es tal que su componente cuya dirección está determinada por una de las coordenadas cartesianas ejes, mientras radial y componentes tangenciales se refieren a la radio de rotación de un objeto como su dirección de referencia. El primero es paralela a la radio y el último es ortogonal a la misma. Ambos permanecen ortogonal al eje de rotación en todo momento. (En dos dimensiones de este requisito se convierte en redundante como eje degenera a un punto de rotación.) La elección de un sistema de coordenadas no afecta a las propiedades de un vector o su comportamiento bajo transformaciones.

Vectores como los derivados direccionales

Un vector también puede ser definido como una derivada direccional: considerar una función 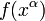y una curva de 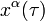. Entonces la derivada direccional de 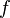se define como un escalar

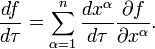
donde el índice 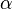es sumada sobre el número apropiado de las dimensiones (por ejemplo, de 1 a 3 en el espacio euclidiano 3-dimensional, de 0 a 3 en el espacio-tiempo de 4 dimensiones, etc.). Entonces considere un vector tangente a :

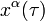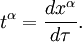
Podemos reescribir la derivada direccional en forma diferencial (sin una función determinada 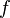) Como

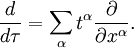
Por tanto, cualquier derivada direccional puede ser identificado con un vector correspondiente, y cualquier vector puede ser identificado con un derivado direccional correspondiente. Por tanto, podemos definir un vector con precisión:

Vectores, pseudovectors y transformaciones

Una caracterización alternativa de vectores espaciales, especialmente en la física, describe vectores como listas de las cantidades que se comportan de cierta manera bajo un transformación de coordenadas. Se requiere un vector para tener componentes que "transforman como las coordenadas" bajo coordinar rotaciones. En otras palabras, si todo el espacio se rotaron, el vector giraría exactamente de la misma manera. Matemáticamente, si el sistema de coordenadas se somete a una rotación descrita por una matriz de rotación R, de modo que un vector de coordenadas x se transforma en x '= x R, entonces cualquier otro vector v debe ser transformado de manera similar a través de v' = R v. Este requisito importante es lo que distingue a un vector espacial de cualquier otro triplete de cantidades significativas físicamente. Por ejemplo, si v consta de las x, y, y z -Componentes de velocidad , entonces v es un vector porque los componentes de la velocidad transforman bajo coordinar los cambios. Por otra parte, por ejemplo, un triplete formado por la longitud, anchura y altura de una caja rectangular podría considerarse como los tres componentes de un resumen de vectores , pero no un vector espacial, ya que la rotación de la caja no se transforma en consecuencia éstos tres componentes. Los ejemplos de vectores incluyen desplazamiento, velocidad , campo eléctrico , impulso , fuerza y aceleración .

En el lenguaje de la geometría diferencial , el requisito de que los componentes de un vector transforman de acuerdo con la misma matriz de la transición de coordenadas es equivalente a la definición de un vector para ser una tensor de rango uno contravariante. Sin embargo, en la geometría diferencial y otras áreas de las matemáticas como teoría de la representación, los "coordinar transiciones" no tiene por qué limitarse a las rotaciones. Otras nociones de vector espacial corresponden a diferentes opciones de grupo de simetría.

Como un caso particular en el que el grupo de simetría es importante, todos los ejemplos anteriores son vectores que "transforman como las coordenadas" bajo tanto adecuada y rotaciones inadecuadas. Un ejemplo de una rotación impropios es una reflejo en el espejo. Es decir, estos vectores se definen de una manera tal que, si todo el espacio se volteó a través de un espejo (o de lo contrario sometidos a una rotación incorrecta), que sería vector voltear alrededor exactamente de la misma manera. Vectores con esta propiedad se llaman vectores verdaderos o vectores polares. Sin embargo, otros vectores se definen de una manera tal que, al mover de un tirón a través de un espejo, el vector voltea de la misma manera, pero también adquiere un signo negativo. Estos se llaman pseudovectors (o vectores axiales), y más comúnmente se producen como productos cruzados de vectores verdaderos.

Un ejemplo de un vector axial es el momento angular . El conducir en un coche , y mirando hacia adelante, cada una de las ruedas tiene un momentum angular del vector que apunta hacia la izquierda. Si el mundo se refleja en un espejo que cambia el lado izquierdo y derecho del coche, el reflejo de este impulso de vector angular puntos a la derecha, pero el vector momento angular real de la rueda sigue apuntando a la izquierda, lo que corresponde a la menos firmar. Otros ejemplos de pseudovectors incluyen campo magnético, par, o más en general, cualquier producto vectorial de dos vectores (true).

Esta distinción entre vectores y pseudovectors es a menudo ignorado, pero se convierte en importante para estudiar la simetría propiedades. Ver paridad (física).