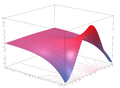
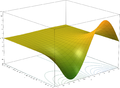
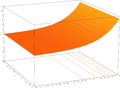
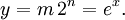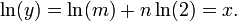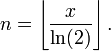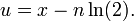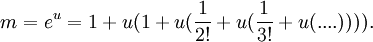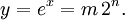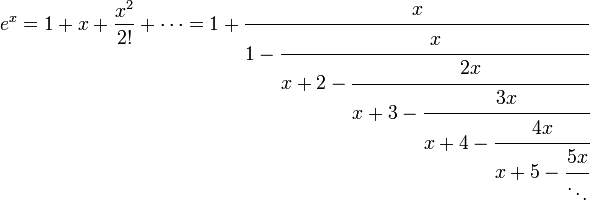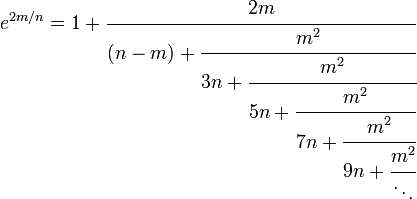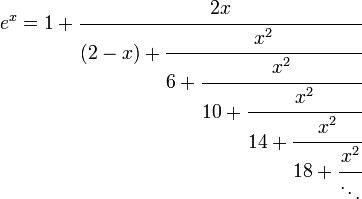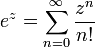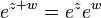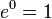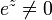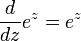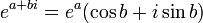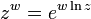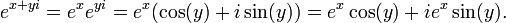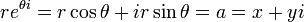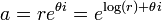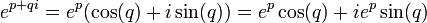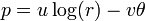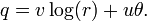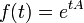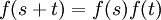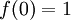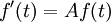Funcion exponencial
Sabías ...
Esta selección Wikipedia está disponible sin conexión de SOS Children para su distribución en el mundo en desarrollo. El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.
La función exponencial es una función de las matemáticas . La aplicación de esta función para un valor x se escribe como exp (x). De manera equivalente, esto se puede escribir en la forma e x, donde e es una constante matemática, la base del logaritmo natural, que es aproximadamente igual a 2,718281828, y también se conoce como Euler número 's.
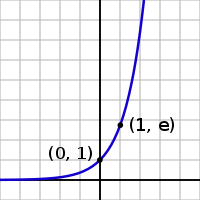
En función de las reales variable x, el gráfica de y = e x es siempre positiva (por encima del eje x) y el aumento (visto de izquierda a derecha). Es nunca toca el eje x, aunque se pone arbitrariamente cerca de ella (por lo tanto, el eje x es una horizontal asíntota de la gráfica). Su función inversa , el logaritmo natural , ln (x), se define para todo x positivo. La función exponencial se denomina ocasionalmente como el anti-logaritmo . Sin embargo, esta terminología parece haber caído en desuso en los últimos tiempos.
A veces, sobre todo en las ciencias , el término función exponencial se usa más generalmente para funciones de la forma ka x, donde a, llamada la base, es cualquier número real positivo no es igual a uno. Este artículo se centrará inicialmente en la función exponencial con base e, el número de Euler.
En general, la variable x puede ser cualquier real o número complejo , o incluso un tipo completamente diferente de objeto matemático; ver la definición formal de abajo .
Propiedades
La mayoría simplemente, funciones exponenciales se multiplican a una velocidad constante. Por ejemplo, la población de un cultivo bacteriano que se duplica cada 20 minutos puede (aproximativamente, ya que esto no es realmente un problema continuo) se expresa como una exponencial, al igual que el valor de un coche que disminuye en un 10% por año.
Usando el logaritmo natural, uno puede definir funciones exponenciales más general. La función
definido para todo a> 0, y todos los números reales x, se llama la función exponencial con la base a. Tenga en cuenta que esta definición de 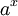 se basa en la existencia previamente establecido de la función de
se basa en la existencia previamente establecido de la función de 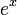 , Definida para todos los números reales. (Aquí, ni formal ni conceptualmente aclarar si existe tal función o qué exponentes no naturales se supone que significa eso.)
, Definida para todos los números reales. (Aquí, ni formal ni conceptualmente aclarar si existe tal función o qué exponentes no naturales se supone que significa eso.)
Tenga en cuenta que la ecuación anterior es válido para a = e, ya
Las funciones exponenciales "traducen entre la suma y multiplicación", como se expresa en los tres primeros y el quinto de las siguientes leyes exponenciales:
Estos son válidas para todos positivos números reales a y b y todos los números x e y real. Expresiones con fracciones y raíces a menudo se pueden simplificar el uso de la notación exponencial:
y, para cualquier a> 0, número real b, y entero n> 1:
Derivados y ecuaciones diferenciales
La importancia de las funciones exponenciales en las matemáticas y las ciencias se debe principalmente a las propiedades de sus derivados . En particular,
Es decir, e x es su propio derivado . Funciones de la forma 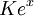 de constante K son las únicas funciones con esa propiedad. (Esto se deduce de la Teorema de Picard-Lindelöf, con
de constante K son las únicas funciones con esa propiedad. (Esto se deduce de la Teorema de Picard-Lindelöf, con 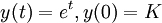 y
y 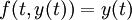 .) Otras formas de decir lo mismo incluyen:
.) Otras formas de decir lo mismo incluyen:
- La pendiente de la gráfica en cualquier punto es la altura de la función en ese punto.
- La tasa de aumento de la función en x es igual al valor de la función en x.
- La función resuelve la ecuación diferencial
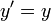 .
. - exp es una punto fijo de derivada como funcional
De hecho, muchas ecuaciones diferenciales dan lugar a funciones exponenciales, incluyendo el Ecuación de Schrödinger y la La ecuación de Laplace, así como las ecuaciones para movimiento armónico simple.
Para las funciones exponenciales con otras bases:
Por lo tanto, cualquier función exponencial es una múltiplo constante de su propio derivado.
Si el crecimiento o decaimiento tasa de una variable es proporcional a su tamaño - como es el caso en el crecimiento ilimitado de la población (véase Catástrofe maltusiana), compuesto continuo interés, o desintegración radiactiva - entonces la variable se puede escribir como una constante por una función exponencial de tiempo.
Además para cualquier función diferenciable f (x), encontramos, por el regla de la cadena:
Definición formal
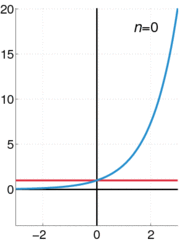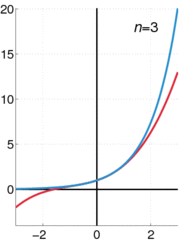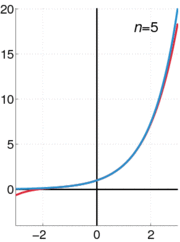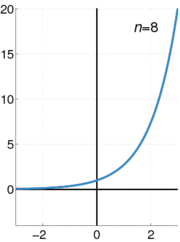
La función exponencial e x se puede definir en una variedad de formas equivalentes, como una serie infinita. En particular, puede ser definida por una serie de potencias :
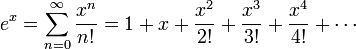 .
.
Tenga en cuenta que esta definición tiene la forma de una serie de Taylor . Utilizando una definición alternativa para la función exponencial debe conducir al mismo resultado cuando se expande como una serie de Taylor .
Una definición menos común define  como la solución
como la solución  a la ecuación
a la ecuación
Valor numérico
Para obtener el valor numérico de la función exponencial, la serie infinita se puede reescribir como:
Esta expresión convergerá rápidamente si podemos asegurar que x es menor que uno.
Para asegurar esto, podemos usar la siguiente identidad.
- Donde
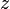 es la parte entera de
es la parte entera de 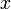
- Donde
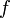 es la parte fraccionaria de
es la parte fraccionaria de 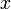
- Por lo tanto,
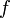 es siempre menor que 1 y
es siempre menor que 1 y 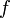 y
y 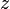 sumar
sumar 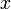 .
.
El valor de la constante e z se puede calcular de antemano mediante la multiplicación e consigo mismo veces z.
Informática exp (x) para x real
Una mejor algoritmo se puede encontrar como sigue.
Primero, note que la respuesta y = e x es por lo general un número de coma flotante representado por un mantisa y un exponente m n de modo y = m 2 n para algún entero n y m adecuadamente pequeño. De este modo, se obtiene:
Tomando registro en ambos lados de los dos últimos nos da:
Por lo tanto, obtenemos n como el resultado de dividir x por log (2) y encontrar el mayor número entero que no es mayor que esto - es decir, el la función del suelo:
Habiendo encontrado n entonces podemos encontrar la parte fraccionaria u como esto:
El número u es pequeña y en el rango 0 ≤ u <ln (2) y para que podamos usar las series mencionadas anteriormente para calcular m:
Tener encontrado myn entonces podemos producir y simplemente combinando los dos en un número de punto flotante:
Fracciones continuas para e x
Vía identidad de Euler:
Técnicas más avanzadas son necesarias para construir el siguiente:
Configuración m = x y n = 2 rendimientos
Cálculo de 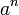 por número natural (entero positivo) n
por número natural (entero positivo) n
No es una forma rápida de calcular 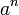 cuando n es un entero positivo. Se hace uso del hecho de que las pruebas de que un número tan es impar es muy fácil en un equipo y dividiendo por 2 también es rápido simplemente cambiando todos los bits a la derecha.
cuando n es un entero positivo. Se hace uso del hecho de que las pruebas de que un número tan es impar es muy fácil en un equipo y dividiendo por 2 también es rápido simplemente cambiando todos los bits a la derecha.
paso 1, inicializar algunas variables
y: = 1, k: = n, f: = a
el paso 2, la prueba de k
si k es 0, vaya al paso 7
el paso 3, (k no es 0 aquí, prueba si k es par)
si k es ni siquiera ir al paso 5
el paso 4, (k es impar aquí, se multiplican en) 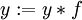
el paso 5, (divide por 2 k / ignore resto, se divide por turno, también cuadrado f)
k: = k desplazamiento a la derecha por 1 f: = f * f
paso 6 (circular)
vuelva al paso 2
el paso 7, (hecho, y es resultado = a n)
volver y
En C se puede escribir el algoritmo de la siguiente manera:
energía doble (doble un unsigned int n) {double y = 1; doble f = a; unsigned int k = n; mientras que (k = 0) {if ((k & 1) = 0!) y * = f; k >> = 1; f * = f; } Return y; }energía doble (doble un unsigned int n) {double y = 1; doble f = a; unsigned int k = n; mientras que (k = 0) {if ((k & 1) = 0!) y * = f; k >> = 1; f * = f; } Return y; }
Mientras que una multiplicación ingenua de un ^ 100 requeriría 100 iteraciones de un bucle multiplicando a, este bucle itera sólo 7 veces (El número 100 se escribe utilizando 7 bits).
Este algoritmo se puede ampliar fácilmente para enteros firmados por realizar los siguientes pasos antes y después:
paso 1. si k es negativo, negar el valor por lo que tenemos un positivo k. n todavía recuerda el valor original.
paso 2. Realizar el cómputo anterior para 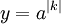
el paso 3. Si n es negativo, invierta el resultado tan y: = 1 / a. y ahora es el resultado de 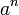 para un entero n.
para un entero n.
En el plano complejo
Como en el verdadero caso, la función exponencial se puede definir en el plano complejo de varias formas equivalentes. Algunas de estas definiciones reflejan las fórmulas para la función exponencial de valor real. En concreto, todavía se puede utilizar la definición de series de potencias, en el que el valor real se sustituye por una compleja:
Usando esta definición, es fácil de demostrar por qué 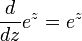 posee en el plano complejo.
posee en el plano complejo.
Otra definición extiende la verdadera función exponencial. En primer lugar, afirmamos la propiedad deseada 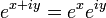 . Para
. Para 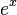 usamos la verdadera función exponencial. Entonces procedemos definiendo solamente:
usamos la verdadera función exponencial. Entonces procedemos definiendo solamente: 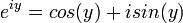 . Así que usamos la verdadera definición en lugar de ignorarlo.
. Así que usamos la verdadera definición en lugar de ignorarlo.
Cuando se considera como una función definida en el plano complejo , la función exponencial conserva las propiedades importantes
para todo z y w.
Es un función holomorfa que es periódica con período imaginario 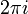 y puede ser escrito como
y puede ser escrito como
donde a y b son valores reales. Esta fórmula se conecta la función exponencial con las funciones trigonométricas y a la funciones hiperbólicas. Vemos, pues, que todos funciones elementales a excepción de los polinomios de brotar de la función exponencial de una manera u otra.
Ver también La fórmula de Euler.
Extendiendo el logaritmo natural de argumentos complejos produce una función de varios valores, ln (z). Entonces podemos definir una exponenciación más general:
para todos los números complejos z y w. Esta es también una función de múltiples valores. Las leyes exponenciales arriba indicados se mantienen fieles si se interpreta correctamente como declaraciones acerca de las funciones de varios valores.
La función exponencial mapas de cualquier línea en el plano complejo a una espiral logarítmica en el plano complejo con el centro en el origen. Dos casos especiales podrían tenerse en cuenta: cuando la línea original es paralelo al eje real, la sprial resultante nunca se cierra sobre sí misma; cuando la línea original es paralelo al eje imaginario, la espiral resultante es un círculo de radio de algunos.
- Los gráficos de la función exponencial en el plano complejo
Cálculo de exp (z) para un complejo z
Esto es bastante sencillo dada la fórmula
Tenga en cuenta que el argumento y de las funciones trigonométricas es real.
Cálculo de 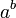 donde tanto a como b son complejos
donde tanto a como b son complejos
Esto también es sencillo dado las fórmulas:
si a = x + yi y b = u + vi lo primero que puede convertir una de coordenadas polares mediante la búsqueda de un 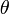 y un
y un  tal que:
tal que:
o
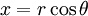 y
y 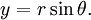
Por lo tanto, 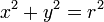 o
o 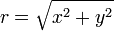 y
y 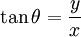 o
o 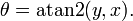
Ahora, tenemos que:
así:
El exponente es, pues, una simple multiplicación de dos valores complejos que producen un resultado complejo que puede ser traído de vuelta a formato cartesiano habitual por la fórmula:
donde p es la parte real de la multiplicación:
y q es la parte imaginaria de la multiplicación:
Tenga en cuenta que todos los 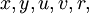
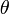 ,
, 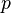 y
y 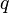 son todos los valores reales en estos cálculos. El resultado de
son todos los valores reales en estos cálculos. El resultado de 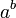 es por lo tanto
es por lo tanto 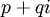 .
.
También tenga en cuenta que, dado que se calcula y uso 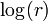 en lugar de r sí usted no tiene que calcular la raíz cuadrada. En su lugar, simplemente calcular
en lugar de r sí usted no tiene que calcular la raíz cuadrada. En su lugar, simplemente calcular 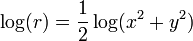 . Cuidado con potencial desbordamiento sin embargo y posiblemente reducir la amplitud del x e y antes de la informática
. Cuidado con potencial desbordamiento sin embargo y posiblemente reducir la amplitud del x e y antes de la informática 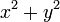 por una potencia adecuada de 2 si
por una potencia adecuada de 2 si 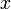 y
y 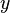 son tan grandes que le desbordarse. Si por el contrario se corre el riesgo de desbordamiento, escalar por una potencia adecuada de 2 antes de calcular la suma de los cuadrados. En cualquier caso, a continuación, obtener la versión a escala de
son tan grandes que le desbordarse. Si por el contrario se corre el riesgo de desbordamiento, escalar por una potencia adecuada de 2 antes de calcular la suma de los cuadrados. En cualquier caso, a continuación, obtener la versión a escala de 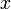 - Podemos llamarlo
- Podemos llamarlo 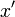 y la versión a escala de
y la versión a escala de 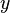 - Llámalo
- Llámalo 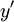 y por lo que se obtiene:
y por lo que se obtiene:
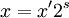 y
y 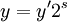
donde 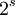 es el factor de escala.
es el factor de escala.
Entonces usted consigue 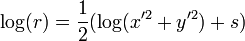 donde
donde 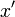 y
y 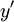 son escalados de modo que la suma de los cuadrados no se desbordará o subdesbordamiento. Si
son escalados de modo que la suma de los cuadrados no se desbordará o subdesbordamiento. Si 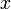 es muy grande, mientras
es muy grande, mientras 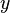 es muy pequeño, por lo que no se puede encontrar un factor de escala tal va desbordar todos modos y por lo que la suma es esencialmente igual a
es muy pequeño, por lo que no se puede encontrar un factor de escala tal va desbordar todos modos y por lo que la suma es esencialmente igual a 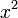 puesto que y se ignora y por lo tanto se obtiene
puesto que y se ignora y por lo tanto se obtiene 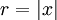 en este caso y
en este caso y 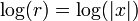 . Lo mismo sucede en el caso cuando
. Lo mismo sucede en el caso cuando 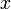 es muy pequeño y
es muy pequeño y 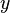 es muy grande. Si ambos son muy grandes o ambos son muy pequeñas se puede encontrar un factor de escala como se mencionó anteriormente.
es muy grande. Si ambos son muy grandes o ambos son muy pequeñas se puede encontrar un factor de escala como se mencionó anteriormente.
Tenga en cuenta que esta función es, en general, varios valores para argumentos complejos. Esto es porque la rotación de un solo punto a través de cualquier ángulo de más de 360 grados, o 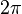 radianes, es el mismo que el ángulo de rotación a través de sí mismo. Así
radianes, es el mismo que el ángulo de rotación a través de sí mismo. Así  anterior no es único:
anterior no es único: 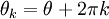 para cualquier entero
para cualquier entero 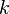 haría también. La convención es sin embargo que cuando
haría también. La convención es sin embargo que cuando 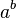 se toma como un solo valor debe ser que para
se toma como un solo valor debe ser que para 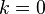 , Es decir. usamos el valor más pequeño posible (en magnitud) de theta, que tiene una magnitud de, como máximo,
, Es decir. usamos el valor más pequeño posible (en magnitud) de theta, que tiene una magnitud de, como máximo, 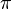 .
.
Matrices y álgebras de Banach
La definición de la función exponencial dada anteriormente se puede utilizar verbatim para cada Banach álgebra, y en particular para cuadrados matrices (en cuyo caso la función se llama la matriz exponencial). En este caso tenemos
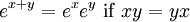
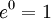
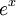 es invertible con inversa
es invertible con inversa 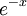
- la derivada de
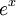 en el punto
en el punto 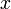 es que el mapa lineal que envía
es que el mapa lineal que envía 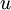 a
a 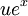 .
.
En el contexto de las álgebras no conmutativas Banach, como álgebras de matrices u operadores en Banach o Espacios de Hilbert, la función exponencial se considera a menudo como una función de un argumento real:
donde A es un elemento fijo de la álgebra y t es cualquier número real. Esta función tiene las propiedades importantes
En álgebras de Lie
La mapa exponencial el envío de una Acuéstese álgebra a la Grupo de Lie que dio lugar a que comparte las propiedades anteriores, lo que explica la terminología. De hecho, dado que R es el álgebra de Lie del grupo de Lie de todos los números reales positivos con la multiplicación, la función exponencial ordinaria para argumentos reales es un caso especial de la situación álgebra de Lie. Del mismo modo, ya que el álgebra de Lie M (n, R) de todas las matrices reales cuadrados pertenece al grupo de Lie de todas las matrices cuadradas invertibles, la función exponencial para matrices cuadradas es un caso especial de la función exponencial álgebra de Lie.
Función exponencial Doble
La función exponencial doble término puede tener dos significados:
- una función con dos términos exponenciales, con diferentes exponentes
- una función
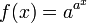 ; este crece incluso más rápido que una función exponencial; Por ejemplo, si a = 10: f (-1) = 1,26, f (0) = 10, f (1) = 10 10, f (2) = 10 100 = googol, ..., f (100) = googolplex.
; este crece incluso más rápido que una función exponencial; Por ejemplo, si a = 10: f (-1) = 1,26, f (0) = 10, f (1) = 10 10, f (2) = 10 100 = googol, ..., f (100) = googolplex.
Los factoriales crecen más rápido que las funciones exponenciales, pero más lento que las funciones de doble exponencial. Números de Fermat, generados por 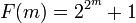 y números dobles de Mersenne generados por
y números dobles de Mersenne generados por 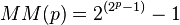 son ejemplos de funciones exponenciales dobles.
son ejemplos de funciones exponenciales dobles.
Inmuebles similares de  y la función de
y la función de 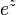
La función 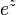 no está en C (z) (es decir. no el cociente de dos polinomios con coeficientes complejos).
no está en C (z) (es decir. no el cociente de dos polinomios con coeficientes complejos).
Para los números complejos n distintas 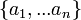 ,
, 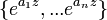 es linealmente independiente sobre C (z).
es linealmente independiente sobre C (z).
La función 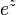 es trascendental sobre C (z).
es trascendental sobre C (z).
Periodicidad
Para todos los enteros n y compleja x:
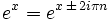
Prueba:
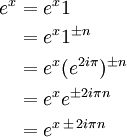
Para todos los enteros positivos n y complejo a & x:
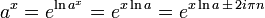


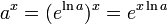
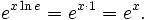
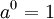
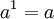
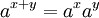
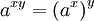
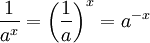
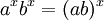
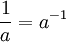
![\, \ Sqrt [n] {a ^ b} = \ left (\ sqrt [n] {a} \ right) ^ b = a ^ {b / n}.](../../images/90/9057.png)
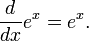
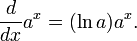
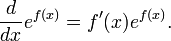
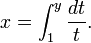
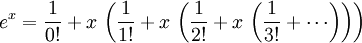
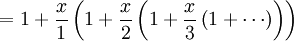
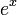
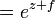
![\, = E ^ z \ épocas \ left [{1 \ over 0!} + F \, \ dejó ({1 \ over 1!} + F \, \ dejó ({1 \ over 2!} + F \, \ left ({1 \ over 3!} + \ cdots \ right) \ right) \ right) \ right]](../../images/90/9079.png)