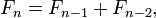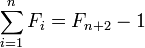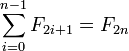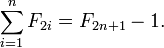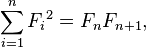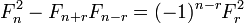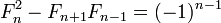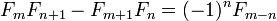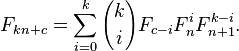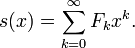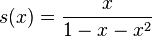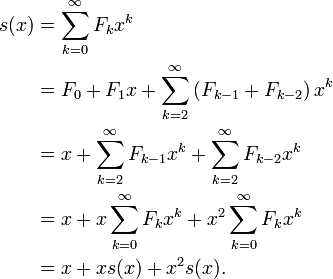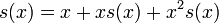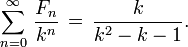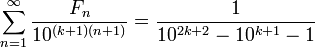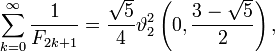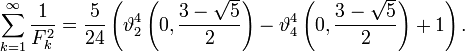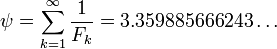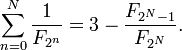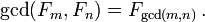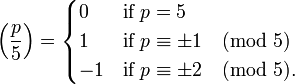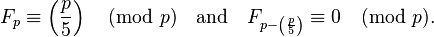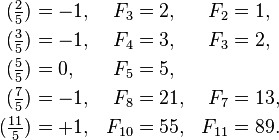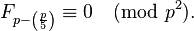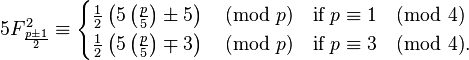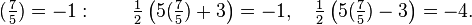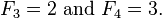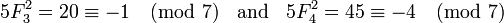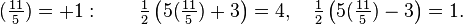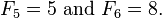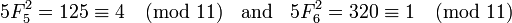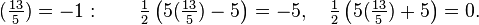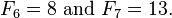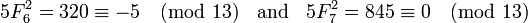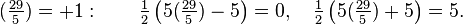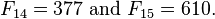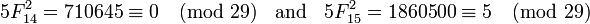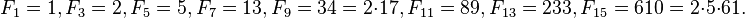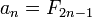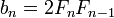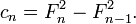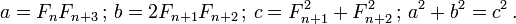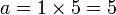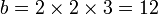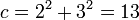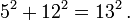Número de Fibonacci
Sabías ...
Esta selección Wikipedia está disponible sin conexión de SOS Children para su distribución en el mundo en desarrollo. Antes de decidir sobre el patrocinio de un niño, ¿por qué no aprender sobre diferentes obras de caridad de patrocinio primero ?
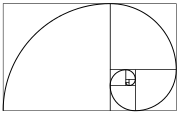
En matemáticas , los números de Fibonacci o series de Fibonacci o secuencia de Fibonacci son los números de la siguiente secuencia de enteros:
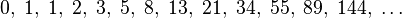 (Secuencia A000045 en OEIS )
(Secuencia A000045 en OEIS )
Por definición, los primeros dos números en la secuencia de Fibonacci son 0 y 1, y cada número subsiguiente es la suma de los dos anteriores.
En términos matemáticos, la secuencia F de n números de Fibonacci se define por la relación de recurrencia
con valores de semilla
La secuencia de Fibonacci se nombra después Leonardo de Pisa, que era conocido como Fibonacci. 1202 El libro de Fibonacci Líber Abad introdujo la secuencia de matemáticas de Europa occidental, aunque la secuencia se había descrito anteriormente en matemáticas indias . Por convención moderna, la secuencia comienza ya sea con F 0 = 0 o 1 con F = 1. El ábacos de Liber comenzó la secuencia con F 1 = 1, sin un 0 inicial.
Números de Fibonacci están estrechamente relacionados con Números de Lucas en que son un par complementario de Secuencias de Lucas. Ellos están íntimamente conectados con la proporción áurea ; Por ejemplo, el aproximaciones racionales más cercanos a la relación son 2/1, 3/2, 5/3, 8/5, .... Las aplicaciones incluyen algoritmos informáticos tales como el Técnica de búsqueda de Fibonacci y la Estructura de datos montón de Fibonacci, y gráficos de llamada Cubos de Fibonacci utilizados para la interconexión de sistemas paralelos y distribuidos. También aparecen en la configuración biológicos, tales como ramificación en los árboles, filotaxis (la disposición de las hojas en un tallo), los brotes de la fruta de un piña, el florecimiento de alcachofa, un défrisage helecho y la disposición de una cono de pino.
Orígenes

La secuencia de Fibonacci aparece en matemáticas indias , en relación con Prosodia sánscrita. En la tradición oral sánscrito, había mucho énfasis en cuánto tiempo se mezclan (L) sílabas con el corto (S), y contando los diferentes patrones de L y S dentro de un determinado resultado de longitud fija en los números de Fibonacci; el número de patrones que son m sílabas cortas de largo es el número de Fibonacci F m + 1.
Susantha Goonatilake escribe que el desarrollo de la secuencia de Fibonacci "se atribuye en parte a Pingala (200 aC), después de ser asociado con Virahanka (c. 700 dC), Gopāla (c. 1135), y Ataudes (c. 1150) ". Parmanand Singh cita críptico cha fórmula misrau de Pingala (" los dos se mezclan ") y cita estudiosos que lo interpretan en el contexto como diciendo que los casos de m latidos (F m + 1) se obtiene sumando una a los casos m F y [L] a los F m -1 casos. Él fechas [S] Pingala antes de 450 aC.
Sin embargo, la exposición más clara de la serie se presenta en la obra de Virahanka (c. 700 dC), cuyo propio trabajo se pierde, pero está disponible en una cita de Gopala (c 1135.):
- Variaciones de dos metros anteriores [es la variación] ... Por ejemplo, para [un metro de longitud] cuatro, variaciones de metros de dos [y] siendo mezclados tres, cinco sucede. [Resuelve ejemplos 8, 13, 21] ... De esta manera, el proceso debe ser seguido en todas Matra-vṛttas [combinaciones prosódicos].
La serie también es discutido por Gopala (antes de 1135 dC) y por el erudito Jain Ataudes (c. 1150).
En Occidente, la secuencia de Fibonacci aparece por primera vez en el libro Líber Abad (1202) por Leonardo de Pisa, conocido como Fibonacci. Fibonacci considera el crecimiento de un (biológicamente realista) idealizada conejo población, suponiendo que: un par recién nacido de conejos, un macho, una hembra, se ponen en un campo; conejos son capaces de aparearse a la edad de un mes, de modo que al final de su segundo mes una hembra puede producir otro par de conejos; conejos nunca mueren y un par de acoplamiento siempre produce un nuevo par (un hombre y una mujer) cada mes a partir del segundo mes. El rompecabezas que Fibonacci planteó fue: ¿cuántos pares habrá en un año?
- Al final del primer mes, se aparean, pero todavía hay sólo 1 par.
- Al final del segundo mes la hembra produce un nuevo par, por lo que ahora hay 2 pares de conejos en el campo.
- Al final del tercer mes, la hembra original, produce un segundo par, haciendo 3 pares en todo en el campo.
- Al final del cuarto mes, la hembra original ha producido otro nuevo par, la hembra nacido hace dos meses produce su primer par también, haciendo 5 pares.
Al final de la n-ésima meses, el número de pares de conejos es igual al número de nuevos pares (que es el número de pares en meses n - 2) más el número de pares vivo mes pasado (n - 1). Este es el enésimo número de Fibonacci.
El nombre de "sucesión de Fibonacci" fue utilizado por primera vez por el teórico número del siglo 19 Édouard Lucas.
Lista de los números de Fibonacci
La primera 21 números Fibonacci F n para n = 0, 1, 2, ..., 20 son:
F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11 F 12 F 13 F 14 F 15 F 16 F 17 F 18 F 19 F 20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765
La secuencia también se puede extender a negativo índice n usando la relación de recurrencia re-dispuesta
que produce la secuencia de números "negafibonacci" satisfactorio
Así, la secuencia es bidireccional
F -8 F -7 F -6 F -5 F -4 F -3 F -2 F -1 F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 -21 13 -8 5 -3 2 -1 1 0 1 1 2 3 5 8 13 21
Ocurrencias en matemáticas

Los números de Fibonacci se producen en las sumas de las diagonales "superficiales" en el triángulo de Pascal (véase el coeficiente binomial ).
Los números de Fibonacci se pueden encontrar en diferentes formas en la secuencia de binario cuerdas.
- El número de cadenas binarias de longitud n sin 1s consecutivos es el número de Fibonacci F n 2. Por ejemplo, de las 16 cadenas binarias de longitud 4, hay F 6 = 8 sin 1s consecutivos - son 0000, 0100, 0010, 0001, 0101, 1000, 1010 y 1001. Por simetría, el número de cadenas de longitud n sin 0s consecutivos es también F n 2.
- El número de cadenas binarias de longitud n sin un número impar de 1s consecutivos es el número Fibonacci F n + 1. Por ejemplo, de las 16 cadenas binarias de longitud 4, hay F 5 = 5 sin un número impar de 1s consecutivos - son 0.000, 0.011, 0.110, 1.100, 1.111.
- El número de cadenas binarias de longitud n sin un número par de 0s o 1s consecutivos es 2 F n. Por ejemplo, de las 16 cadenas binarias de longitud 4, hay 2 F 4 = 6 sin un número par de 0s o 1s consecutivos - son 0.001, 1.000, 1.110, 0.111, 0.101, 1.010.
Relación con la proporción áurea
De forma cerrada expresión
Como cada secuencia definida por una recurrencia lineal con coeficientes constantes, los números de Fibonacci tienen una solución de forma cerrada. Se ha dado a conocer como La fórmula de Binet, a pesar de que ya era conocido por Abraham de Moivre:
donde
es la proporción áurea (secuencia A001622 en OEIS ), y
Para ver esto, tenga en cuenta que φ y ψ son dos soluciones de las ecuaciones
por lo que los poderes de φ y ψ satisfacen la recursividad de Fibonacci. En otras palabras
y
De ello se deduce que para cualquier valores de a y b, la secuencia definida por
satisface la misma recurrencia
Si A y B se eligen de manera que U 0 = 0 y T = 1 1 a continuación, la secuencia resultante U n debe ser la secuencia de Fibonacci. Esto es lo mismo que exigir a y b satisfacer el sistema de ecuaciones:
que tiene solución
la producción de la fórmula requerida.
Computación redondeando
Desde
para todo n ≥ 0, el número F n es el número entero más cercano de
Por lo tanto, se puede encontrar redondeo, o en términos de la la función del suelo:
O la función de número entero más cercano:
Del mismo modo, si ya sabemos que el número F> 1 es un número Fibonacci, podemos determinar su índice dentro de la secuencia de
Límite de cocientes consecutivos
Johannes Kepler observó que la relación de los números de Fibonacci consecutivos converge. Escribió que "como 5 es a 8, de modo es de 8 a 13, en la práctica, y como 8 es 13, por lo que es casi 13 a 21", y concluyó que el límite se acerca la relación φ oro.
Esta convergencia no depende de los valores de partida elegidos, excluyendo 0, 0. Por ejemplo, los valores iniciales 19 y 31 generan la secuencia 19, 31, 50, 81, 131, 212, 343, 555 ... etc. La proporción de términos consecutivos en esta secuencia muestra la misma convergencia hacia la proporción áurea.
De hecho, esto es válido para cualquier secuencia que satisface la recurrencia Fibonacci que no sea una secuencia de 0 de. Esto puede ser derivado de la fórmula de Binet .
Otra consecuencia es que el límite de la relación de dos números de Fibonacci compensado por una desviación finita en particular en el índice corresponde a la relación de oro planteado por esa desviación. O, en otras palabras:
La descomposición de los poderes de la razón áurea
Dado que la proporción de oro satisface la ecuación
esta expresión se puede utilizar para descomponer poderes superiores φ n como una función lineal de las potencias más bajas, que a su vez puede ser descompuesto todo el camino hacia abajo a una combinación lineal de φ y 1. El resultante relaciones de recurrencia producen números de Fibonacci como los coeficientes lineales:
Esta ecuación puede ser probado por inducción sobre n.
Esta expresión también es cierto para n <1 si la secuencia de Fibonacci F n es extendido a números enteros negativos utilizando la regla de Fibonacci 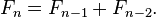
Forma de matriz
Un sistema de 2 dimensiones lineales ecuaciones diferenciales que describen la secuencia de Fibonacci es
Los valores propios de la matriz A son 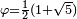 y
y 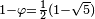 , Y los elementos de los vectores propios de A,
, Y los elementos de los vectores propios de A, 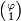 y
y 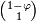 , Se encuentran en las proporciones y φ 1-φ El uso de estos hechos, así como las propiedades de los valores propios, podemos derivar una fórmula directa para el enésimo elemento de la serie de Fibonacci como función analítica de n:
, Se encuentran en las proporciones y φ 1-φ El uso de estos hechos, así como las propiedades de los valores propios, podemos derivar una fórmula directa para el enésimo elemento de la serie de Fibonacci como función analítica de n:
La matriz tiene un determinante de -1, y por lo tanto se trata de un 2 × 2 matriz unimodular. Esta propiedad puede ser entendida en términos de la seguido representación fracción de la proporción áurea:
Los números de Fibonacci ocurrir como la relación de convergentes sucesivos de la fracción continua de φ, y la matriz formada a partir convergentes sucesivos de cualquier fracción continua tiene un determinante de 1 o -1.
La representación de la matriz da la siguiente expresión cerrada para los números de Fibonacci:
Tomando el determinante de ambos lados de esta ecuación rendimientos La identidad de Cassini
Además, desde 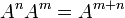 para cualquier matriz cuadrada A, las siguientes identidades pueden derivar:
para cualquier matriz cuadrada A, las siguientes identidades pueden derivar:
En particular, con m = n,
Estas dos últimas identidades ofrecen una forma de calcular los números de Fibonacci de forma recursiva en O (log (n)) para las operaciones aritméticas y en tiempo O (M (n) log (n)), donde M (n) es el tiempo para la multplication de dos número de n dígitos. Esto coincide con el tiempo para calcular el n-ésimo número de Fibonacci partir de la fórmula de la matriz de forma cerrada, pero con menos pasos redundantes si se evita para volver a calcular una ya calcula número de Fibonacci (recursión con memorización).
Reconociendo los números de Fibonacci
La pregunta puede surgir si un entero positivo z es un número Fibonacci. Desde F (n) es el número entero más cercano de 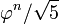 , La, prueba de fuerza bruta más directa es la identidad
, La, prueba de fuerza bruta más directa es la identidad
cual es verdad si y sólo si z es un número Fibonacci. En esta fórmula, F (n) puede ser calculada utilizando rápidamente cualquiera de las anteriormente discutidas expresiones de forma cerrada.
Una implicación de la expresión anterior es la siguiente: si se sabe que un número z es un número Fibonacci, podemos determinar un n tal que F (n) = z por el siguiente:
Alternativamente, un número entero positivo z es un número Fibonacci si y sólo si una de 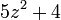 o
o 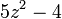 es un cuadrado perfecto.
es un cuadrado perfecto.
Una prueba de un poco más sofisticado utiliza el hecho de que la convergentes de la fracción continua representación de φ son cocientes de los números de Fibonacci sucesivos. Es decir, la desigualdad
(Con coprimero enteros positivos p, q) es verdadera si y sólo si p y q son números de Fibonacci sucesivos. De esto se deriva el criterio de que z es un número Fibonacci si y sólo si el intervalo cerrado
contiene un número entero positivo. Para z ≥ 2, es fácil demostrar que este intervalo contiene a lo sumo un número entero, y en el caso de que z es un número Fibonacci, el entero contenida es igual al siguiente número Fibonacci sucesivos después de z. Algo notable, este resultado aún es válido para el caso z = 1, pero hay que señalar cuidadosamente desde el 1 aparece dos veces en la sucesión de Fibonacci, y por lo tanto tiene dos sucesores distintos.
Identidades combinatorias
La mayoría de las identidades que se usan números de Fibonacci se pueden probar usando argumentos combinatorios utilizando el hecho de que F n se puede interpretar como el número de secuencias de 1s y 2s que suma hasta n - 1. Esto se puede tomar como la definición de F n, con la convención de que F 0 = 0, que significa que no suma se suman a -1, y que F 1 = 1, es decir, la suma vacío se "suman" a 0. Aquí el orden de los asuntos de sumandos. Por ejemplo, 1 + 2 + 1 y 2 se consideran dos sumas diferentes.
Por ejemplo, la relación de recurrencia
o en palabras, el n-ésimo número de Fibonacci es la suma de los dos números anteriores de Fibonacci, pueden dar muestra dividiendo el F (n) sumas de 1s y 2s que se suman a n -1 en dos grupos que no se solapan. Un grupo contiene esas sumas cuyo primer término es 1 y el otro esas sumas cuyo mandato primero es 2. En el primer grupo los términos restantes añadir a n - 2, por lo que tiene F (n -1) sumas, y en el segundo grupo los términos restantes se suman a n-3, por lo que hay F (n -2) sumas. Así que hay un total de F (n-1) + F n -2) sumas por completo, mostrando esto es igual a F (n).
Del mismo modo, se puede demostrar que la suma de los números de Fibonacci primero hasta el n-ésimo es igual a la (n + 2) -nd Fibonacci menos el número 1. En símbolos:
Esto se hace dividiendo las sumas añadiendo a n + 1 de una manera diferente, esta vez por la ubicación de la primera 2. En concreto, el primer grupo consiste de dichas cantidades que comienzan con 2, el segundo grupo los que empiezan 1 + 2 , el tercero 1 + 1 + 2, y así sucesivamente, hasta que el último grupo que se compone de la suma única donde se utilizan sólo 1 de. El número de sumas en el primer grupo es F (n), F (n - 1) en el segundo grupo, y así sucesivamente, con 1 suma en el último grupo. Así que el número total de sumas es F (n) + F (n -1) + ... + F (1) 1 y por lo tanto esta cantidad es igual a F (n 2)
Un argumento similar, que agrupa a las sumas por la posición de la primera 1 en lugar de los 2 primeros, da dos más de las identidades:
y
En palabras, la suma de los primeros números de Fibonacci con índice impar hasta F 2 n -1 es el (2n) -ésimo número de Fibonacci, y la suma de los primeros números de Fibonacci, incluso con índice hasta F 2 n es el (2n + 1) -San número Fibonacci menos 1.
Un truco diferente puede ser usado para probar
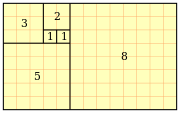
o en palabras, la suma de los cuadrados de los primeros números de Fibonacci hasta F n es el producto de la n-ésima y (n 1) -St números de Fibonacci. En este caso nota de que Fibonacci rectángulo de tamaño n F por F (n 1) se puede descomponer en cuadrados de tamaño n F, F n -1, y así sucesivamente hasta F 1 = 1, de la que la identidad sigue por áreas que comparan .
Otras identidades
Hay muchas otras identidades que pueden derivarse utilizando diversos métodos. Algunos de los más notables son:
Identidad del catalán:
Identidad de la Cassini:
la identidad del d'Ocagne:
donde L n es el n 'th Número Lucas. La última es una identidad para duplicar n; otras identidades de este tipo son
por la identidad de la Cassini.
Estos se pueden encontrar experimentalmente usando reducción de celosía, y son útiles en la creación de la especial tamiz campo número a Factorizar un número de Fibonacci.
Más generalmente,
Poner k = 2 en esta fórmula, se obtiene de nuevo las fórmulas de la final de la sección anterior forma Matrix .
Series de potencias
La función de generación de la secuencia de Fibonacci es la serie de potencias
Esta serie es convergente para 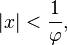 y su suma tiene una forma cerrada simple:
y su suma tiene una forma cerrada simple:
Esto se puede comprobar mediante el uso de la repetición de Fibonacci para expandir cada coeficiente en la suma infinita:
La solución de la ecuación
para s (x) se traduce en la forma cerrada anteriores.
Si x es la inversa de un número entero, la forma cerrada de la serie se convierte
En particular,
para todos los enteros no negativos k.
Algunos matemáticas rompecabezas-libros presentes como curiosidad el valor particular 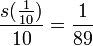 .
.
Sumas Recíprocos
Sumas infinitas más de los números de Fibonacci recíprocas a veces pueden ser evaluados en términos de funciones theta. Por ejemplo, podemos escribir la suma de todos los números de Fibonacci recíproca y pico indexado como
y la suma de los números de Fibonacci recíprocos como cuadrados
Si sumamos 1 a cada número de Fibonacci en la primera suma, existe también la forma cerrada
y hay una bonita suma anidada de los números de Fibonacci cuadrados que dan la inversa de la proporción áurea ,
Resultados como estos hacen que sea posible que una fórmula cerrada para la suma simple de los números de Fibonacci recíprocas se pudo encontrar, pero ninguno es todavía conocida. A pesar de ello, la recíproca constante Fibonacci
se ha demostrado irracional por Richard André-Jeannin.
Serie Millin da una identidad notable:
que se desprende de la forma cerrada para sus sumas parciales cuando n tiende a infinito:
Primes y divisibilidad
Propiedades de divisibilidad
Cada tercio número de la secuencia es incluso y más generalmente, cada k-ésimo número de la secuencia es un múltiplo de F k. Así, la secuencia de Fibonacci es un ejemplo de una secuencia divisibilidad. De hecho, la secuencia de Fibonacci satisface la propiedad divisibilidad fuerte
Primos de Fibonacci
Un primer Fibonacci es un número Fibonacci que es primordial . Los primeros son los siguientes:
- 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ... (secuencia A005478 en OEIS ).
Fibonacci imprima con el se han encontrado miles de dígitos, pero no se sabe si hay infinitamente muchos.
F kn es divisible por n F, por lo que, aparte de F 4 = 3, cualquier primer Fibonacci debe tener un índice prima. Como hay arbitrariamente largas carreras de números compuestos, hay, por tanto, también arbitrariamente tandas largas de números de Fibonacci compuestos.
Con las excepciones de 1, 8 y 144 (F 1 = F 2, F 6 F y 12) cada número Fibonacci tiene un factor primordial que no es un factor de cualquier número de Fibonacci más pequeño ( El teorema de Carmichael).
El único no trivial plaza número de Fibonacci es 144. Atila Pethő demostró en 2001 que sólo hay un número finito de números de Fibonacci potencia perfectos. En 2006, Y. Bugeaud, M. Mignotte, y S. Siksek demostraron que el 8 y 144 son las únicas potencias perfectas no triviales.
No hay un número Fibonacci mayor que F 6 = 8 es un mayor o un menor que un número primo.
Cualquiera de las tres números de Fibonacci consecutivos, tomados de dos en dos, son primos: es decir,
- mcd (F n, F n + 1) = mcd (F n, M n 2) = 1.
Más generalmente,
- mcd (n F, F m) = F mcd (n, m).
Divisores primos de los números de Fibonacci
La divisibilidad de los números de Fibonacci por un primo p es relacionado con el Símbolo de Legendre 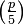 que se evalúa de la siguiente manera:
que se evalúa de la siguiente manera:
Si p es un número primo, entonces
Por ejemplo,
No se sabe si existe un primo p tal que
Tales números primos (si hay alguno) serían llamados Wall-Sun-Sun ceba.
Además, si p ≠ 5 es un número primo impar entonces:
Ejemplo 1. p = 7, en este caso p ≡ 3 (mod 4) y tenemos:
Ejemplo 2. p = 11, en este caso p ≡ 3 (mod 4) y tenemos:
Ejemplo 3. p = 13, en este caso p ≡ 1 (mod 4) y tenemos:
Ejemplo 4. p = 29, en este caso p ≡ 1 (mod 4) y tenemos:
Para n impar, todos los divisores primos impares de F n son congruentes a 1 modulo 4, lo que implica que todos los divisores impares de F (n como los productos de divisores primos impares) son congruentes con 1 módulo 4.
Por ejemplo,
Todos los factores conocidos de Fibonacci números F (i) para todo i <50000 se recogen en los depósitos correspondientes.
Periodicidad módulo n
Se puede ver que si se toman los miembros de la secuencia de Fibonacci mod n, la secuencia resultante debe ser periódica de período a lo sumo n 2 -1. Las longitudes de los periodos para diversos n forman la llamada Períodos Pisano (secuencia A001175 en OEIS ). La determinación de los períodos de Pisano, en general, es un problema abierto, aunque para cualquier particular, n puede ser resuelto como una instancia de detección de ciclo.
Triángulos rectángulos
Comenzando con 5, cada segundo número de Fibonacci es la longitud de la hipotenusa de un triángulo rectángulo con lados de números enteros, o en otras palabras, el número más grande en una Terna pitagórica. La longitud de la pierna más larga de este triángulo es igual a la suma de los tres lados del triángulo precedente en esta serie de triángulos, y la pata más corta es igual a la diferencia entre el número de Fibonacci bypass anterior y la pata más corta de la anterior triángulo.
El primer triángulo en esta serie tiene lados de longitud 5, 4 y 3. Saltarse 8, el siguiente triángulo tiene lados de longitud 13, 12 (5 + 4 + 3), y 5 (8 - 3). Saltarse 21, el siguiente triángulo tiene lados de longitud 34, 30 (13 + 12 + 5), y 16 (21 - 5). Esta serie continúa indefinidamente. Los lados del triángulo a, b, c pueden calcularse directamente:
Estas fórmulas satisfacen 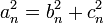 para todo n, pero sólo representan lados del triángulo cuando n> 2.
para todo n, pero sólo representan lados del triángulo cuando n> 2.
Cualquier cuatro números Fibonacci consecutivo F n, F n 1, n 2 F y F n 3 también se puede utilizar para generar un triple de Pitágoras de una manera diferente:
Ejemplo 1: dejar que los números de Fibonacci ser 1, 2, 3 y 5. A continuación:
Magnitud
Desde F n es asintótica a 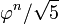 , El número de dígitos en F n es asintótica a
, El número de dígitos en F n es asintótica a 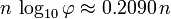 . Como consecuencia, para cada entero d> 1 hay 4 o 5 números de Fibonacci con los dígitos decimales d.
. Como consecuencia, para cada entero d> 1 hay 4 o 5 números de Fibonacci con los dígitos decimales d.
Más en general, en la representación base b, el número de dígitos en F n es asintótica a 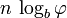 .
.
Aplicaciones
Los números de Fibonacci son importantes en el análisis computacional de tiempo de ejecución de El algoritmo de Euclides para determinar el máximo común divisor de dos enteros: el peor caso de entrada para este algoritmo es un par de números de Fibonacci consecutivos.
Yuri Matiyasevich fue capaz de demostrar que los números de Fibonacci se pueden definir por un Diophantine ecuación, lo que llevó a su solución original de Décimo problema de Hilbert.
Los números de Fibonacci son también un ejemplo de una secuencia completa. Esto significa que todo entero positivo se puede escribir como la suma de los números de Fibonacci, donde se utiliza un solo número una vez como máximo. Específicamente, cada número entero positivo se puede escribir de una manera única como la suma de uno o más números de Fibonacci distintas de tal manera que la suma no incluye ninguna dos números de Fibonacci consecutivos. Esto se conoce como El teorema de Zeckendorf, y una suma de los números de Fibonacci que satisface estas condiciones se llama representación Zeckendorf. La representación Zeckendorf de un número se puede utilizar para derivar su Fibonacci codificación.
Números de Fibonacci se utilizan por algunos generadores de números pseudoaleatorios.
Números de Fibonacci se utilizan en una versión polifásico de la fusionar algoritmo de ordenación en la que una lista no seleccionados se divide en dos listas cuyas longitudes corresponden a secuencial números de Fibonacci - dividiendo la lista para que las dos partes tienen longitudes en el φ proporción aproximada. Una aplicación de unidad de cinta de la combinación polifásica especie fue descrita en The Art of Computer Programming.
Números de Fibonacci surgen en el análisis de la Estructura de datos montón de Fibonacci.
La Cubo de Fibonacci es una grafo no dirigido con un número Fibonacci de nodos que se ha propuesto como una topología de red para computación paralela.
Un método de optimización unidimensional, llamado Técnica de búsqueda de Fibonacci, utiliza los números de Fibonacci.
La serie de números de Fibonacci se utiliza para opcional compresión con pérdida en el IFF 8SVX formato de archivo de audio utilizado en Ordenadores Amiga. La serie de números compands la onda de audio original similar a los métodos logarítmicas tales como μ-law.
Desde el factor de conversión de 1.609344 por millas a kilómetros se encuentra cerca de la proporción áurea (φ denota), la descomposición de la distancia en millas en una suma de los números de Fibonacci se vuelve casi la suma kilómetro cuando los números de Fibonacci son sustituidos por sus sucesores. Este método equivale a una radix número 2 registrarse en oro φ base de la relación que se desplaza. Para convertir de kilómetros a millas, cambiar el registro por la secuencia de Fibonacci en su lugar.
En naturaleza
Secuencias de Fibonacci aparecen en contextos biológicos, en dos números de Fibonacci consecutivos, como ramificación de los árboles, disposición de las hojas en un tallo, los frutos jóvenes de un piña, el florecimiento de alcachofa, un helecho défrisage y la disposición de una cono de pino. Además, numerosas reclamaciones mal fundamentados de los números de Fibonacci o secciones de oro en la naturaleza se encuentran en fuentes populares, por ejemplo, en relación con la cría de conejos en el propio ejemplo realista de Fibonacci, las semillas de girasol, las espirales de las conchas, y la curva de olas. Los números de Fibonacci también se encuentran en el árbol genealógico de las abejas.
Przemyslaw Prusinkiewicz avanzó la idea de que los casos reales pueden en parte ser entendidas como la expresión de ciertas restricciones algebraicas en grupos libres, específicamente como cierta Gramáticas Lindenmayer.
Un modelo para el patrón de floretes en la cabeza de un girasol fue propuesta por H. Vogel en 1979. Esto tiene la forma
donde n es el número de índice de la flósculo y c es un factor de escala constante; así los floretes se encuentran en espiral de Fermat. El ángulo de divergencia, aproximadamente 137,51 °, es el ángulo de oro, dividiendo el círculo en el número áureo. Debido a que esta relación es irracional, no flósculo tiene un vecino en exactamente el mismo ángulo desde el centro, por lo que los flósculos paquete de manera eficiente. Debido a las aproximaciones racionales a la proporción áurea son de la forma F ( j ): F ( j + 1), los vecinos más cercanos de la serie florete n son los que están en n ± F ( j ) de algún índice j que depende de r , la distancia desde el centro. A menudo se dice que los girasoles y arreglos similares tienen 55 espirales en un sentido y 89 en la otra (o algún otro par de números de Fibonacci adyacentes), pero esto es cierto sólo de una gama de radios, por lo general el más exterior y por lo tanto más conspicuo.
El código de la ascendencia de abeja
Números de Fibonacci también aparecen en la descripción de la reproducción de una población de abejas idealizadas, de acuerdo con las siguientes reglas:
- Si un huevo es puesto por una mujer sin pareja, que trama un hombre ozumbido de las abejas.
- Si, sin embargo, un huevo fue fertilizado por un macho, una hembra que eclosiona.
Por lo tanto, una abeja macho siempre tendrá uno de los padres, y una abeja hembra tendrá dos.
Si uno traza la ascendencia de cualquier abeja macho (1 de abeja), tiene 1 padre (1 de abeja), 2 abuelos, bisabuelos 3, 5 tatara-tatara-abuelos, y así sucesivamente. Esta secuencia de números de los padres es la secuencia de Fibonacci. El número de los antepasados en cada nivel, F n , es el número de antepasados femeninos, que es F n-1 , más el número de antepasados masculinos, que es F n-2 . Esto es en el supuesto poco realista de que los antepasados de cada nivel son de otra manera no relacionada.
Cultura popular
Las generalizaciones
La secuencia de Fibonacci se ha generalizado en muchas maneras. Éstas incluyen:
- Generalizando el índice de enteros negativos para producir losNegafibonaccinúmeros.
- Generalizando el índice para los números reales utilizando una modificación de la fórmula de Binet.
- Comenzando con otros números enteros.números de Lucas hanL 1= 1,L 2= 3, yLn=L n-1+L n-2.Primefree utilizan secuencias de la recursión Fibonacci con otros puntos de partida con el fin de generar secuencias en las que todos los números sonde material compuesto.
- Dejar que un número ser una función lineal (aparte de la suma) de los 2 números precedentes. La números de Pell tienenPn= 2P n- 1+P n- 2.
- No sumando los números inmediatamente anteriores. La Padovan y secuencia denúmeros de Perrin tienenP(n) =P(n- 2) +P(n- 3).
- Generando el siguiente número añadiendo 3 números (números tribonacci), 4 números (números tetranacci), o más. Las secuencias resultantes se conocen como números de Fibonacci n-Step .
- Adición de otros objetos de números enteros, por ejemplo, funciones o cuerdas -uno ejemplo esencial espolinomios de Fibonacci.


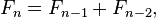
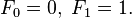
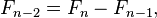
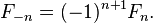
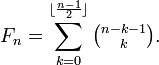
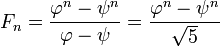
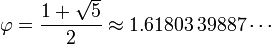
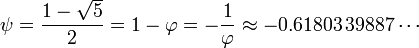
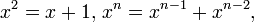
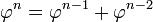
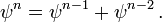
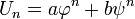
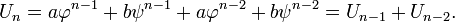
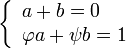
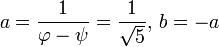
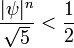
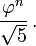
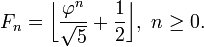
![F_n = \ Bigg [\ frac {\ varphi ^ n} {\ sqrt 5} \ Bigg], \ n \ geq 0.](../../images/2741/274107.png)
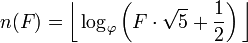
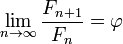
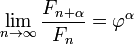
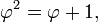
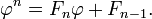
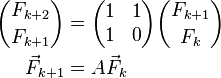
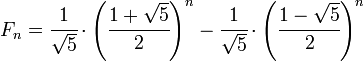
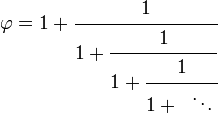
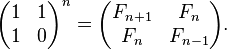
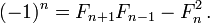
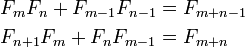
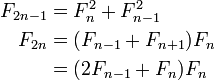
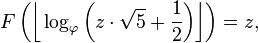
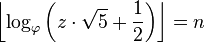
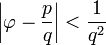
![\ Bigg [\ varphi z \ frac {1} {z}, \ varphi z + \ frac {1} {z} \ Bigg]](../../images/2741/274132.png)