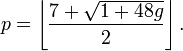Teorema de los cuatro colores
Sabías ...
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . patrocinio SOS Niño es cool!

El teorema de los cuatro colores (también conocido como el mapa de cuatro colores teorema) señala que, dado cualquier plano separado en regiones, tales como un mapa político de los estados de un país, las regiones pueden ser coloreadas usando no más de cuatro colores de tal manera que no hay dos regiones adyacentes reciben el mismo color. Dos regiones se llaman adyacentes sólo si comparten un segmento de frontera, no sólo un punto. Cada región debe estar contiguas: es decir, que no puede tener enclaves como algunos países reales, tales como Angola , Azerbaiyán , el de Estados Unidos o Rusia .
A menudo es el caso que el uso de sólo tres colores es inadecuada. Esto ya se aplica al mapa con una región rodeada por otras tres regiones (aunque con un número par de países que rodean tres colores son suficientes) y no es en absoluto difícil probar que cinco colores son suficientes para colorear un mapa.
El teorema de los cuatro colores fue la primera gran teorema no se ha demostrado que utilizar un ordenador, y la prueba no es aceptada por todos los matemáticos, ya que sería inviable para un ser humano para verificar con la mano (ver asistida por ordenador la prueba). En última instancia, para poder creer la prueba, uno tiene que tener fe en la exactitud de la compilador y hardware de ejecutar el programa utilizado para la prueba.
La percepción de falta de elegancia matemática por la comunidad matemática general fue otro factor, y parafraseando a los comentarios de la época, "una buena prueba matemática es como un poema-este es un directorio telefónico! "
Historia
La conjetura fue propuesto por primera vez en 1852, cuando Francis Guthrie, mientras trata de colorear el mapa de los condados de Inglaterra , se dio cuenta de que se necesitaban sólo cuatro colores diferentes. En ese momento, el hermano de Guthrie, Fredrick, era un estudiante de Augustus De Morgan en Universidad. Francis preguntó con Fredrick respecto a ella, que luego lo llevó a DeMorgan. (Fredrick Guthrie graduó más adelante en 1852, y más tarde se convirtió en profesor de matemáticas en Sudáfrica ). Según De Morgan:
Un alumno mío [Guthrie] me pidió hoy a darle una razón a un hecho que yo no sabía era un hecho - y sin embargo no lo hago. Él dice que si una figura se divide de todos modos y los compartimentos de color diferente para que figuras con cualquier parte de la línea límite común son de color diferente - cuatro colores pueden querían, pero no más, el siguiente es el caso en el que se quieren cuatro colores. Query puede no una necesidad para cinco o más se inventó ...
La primera referencia publicado es por Arthur Cayley, quien a su vez acredita la conjetura de De Morgan.
Hubo varios intentos fallidos de principios de la prueba de la teorema . Una prueba del teorema fue dada por Alfred Kempe en 1879, que fue ampliamente aclamado; otra prueba fue dada por Peter Guthrie Tait en 1880. No fue sino hasta 1890 que la prueba de Kempe se demostró errónea por Percy Heawood, y 1891 que la prueba de Tait se demostró errónea por Julius Petersen-cada prueba falsa de pie sin respuesta desde hace 11 años.
En 1890, además de la exposición de la falla en la prueba de Kempe, Heawood demostró que todos grafos planos son cinco verosímil; ver cinco teorema de color.
Los resultados más significativos se produjeron mediante croata matemático Danilo Blanuša en la década de 1940 por la búsqueda de un original snark.
Durante la década de 1960 y 1970 alemán matemático Heinrich Heesch desarrollado métodos de aplicación de la informática en la búsqueda de una prueba.
No fue sino hasta 1976 que la conjetura de los cuatro colores fue finalmente probada por Kenneth Appel y Wolfgang Haken en el Universidad de Illinois. Fueron asistidos en algún trabajo algorítmico por John Koch.
Si la conjetura de los cuatro colores eran falsas, habría al menos un mapa con el menor número posible de regiones que requiere de cinco colores. La prueba mostró que un contraejemplo tales mínima no puede existir a través de la utilización de dos conceptos técnicos:
- Un conjunto inevitable contiene regiones de tal manera que cada mapa debe tener al menos una región de esta colección.
- Una configuración reducible es una disposición de los países que no pueden ocurrir en un contraejemplo mínimo. Si un mapa contiene una configuración reducible, y el resto del mapa puede ser de color con cuatro colores, a continuación, todo el mapa puede ser coloreado con cuatro colores y por lo que este mapa no es mínima.
El uso de normas y procedimientos matemáticos basados en las propiedades de configuraciones reducibles (por ejemplo, la método de descarga, anillos, cadenas Kempe, etc.), Appel y Haken encontró un conjunto inevitable de configuraciones reducibles, demostrando así que no podría existir un contraejemplo mínimo a la conjetura de los cuatro colores. Su prueba reduce la infinidad de posibles mapas de 1936 configuraciones reducibles (más tarde reducido a 1476), que tuvo que ser comprobada uno por uno por equipo. Esta parte reducibilidad de la obra fue independiente doble comprobarse con diferentes programas y computadoras. Sin embargo, la parte inevitabilidad de la prueba fue de más de 500 páginas de venta libre contra-ejemplos-escritas a mano, gran parte de los cuales era el hijo adolescente de Haken Lippold verificación colorantes gráfico. El programa de ordenador corrió durante cientos de horas.
Desde la experimentación del teorema, algoritmos eficientes se han encontrado mapas de 4 colorantes que requieren sólo O (n 2) el tiempo, donde n es el número de vértices. En 1996 , Neil Robertson, Daniel P. Sanders, Paul Seymour, y Robin Thomas crearon un algoritmo de tiempo cuadrática, utilizando El trabajo de Edward Belaga para mejorar un algoritmo basado en la prueba de cuarto grado Appel y Haken del. Esta nueva prueba es similar a Appel y Haken de pero más eficiente, ya que reduce la complejidad del problema y requiere la comprobación sólo 633 configuraciones reducibles. Tanto las partes inevitabilidad y reducibilidad de esta nueva prueba deben ser ejecutadas por ordenador y no son prácticos para comprobar a mano.
En 1980, George Spencer-Brown depositó su supuesta prueba del mapa de cuatro colores teorema en el Real Sociedad. La validez de esta prueba, que conforma el Anexo 5 de la traducción al alemán de su libro " Leyes de la Forma "(Lübeck 1997), es generalmente dudaban.
En el año 2004 Benjamin y Werner Georges Gonthier formalizó una demostración del teorema dentro de la Coq asistente de prueba (Gonthier, sf). Esto elimina la necesidad de confiar en los diversos programas de ordenador utilizados para verificar los casos particulares; sólo es necesario confiar en el kernel Coq.
También hay algoritmos eficientes para determinar si 1 o 2 colores bastan para colorear un mapa. La determinación de si 3 colores son suficientes, sin embargo, NP-completo, y por lo tanto es poco probable que un algoritmo rápido. La determinación de si un general (posiblemente no plana) gráfico puede ser de 4 de color es igualmente NP-completo.
No por cartógrafos
Aunque el teorema de los cuatro colores fue descubierto en el proceso de colorear un mapa real, rara vez se utiliza en la práctica cartografía. Según Kenneth mayo, un historiador matemático que estudió una muestra de los atlas en la Biblioteca del Congreso, no existe una tendencia a minimizar el número de colores utilizados. Muchos mapas utilizan el color para cosas distintas de las regiones políticas. La mayoría de los mapas utilizan más de cuatro colores, y cuando se utilizan solamente cuatro colores, por lo general el número mínimo de colores en realidad se necesita es menos de cuatro.
En la mayoría de los mapas reales existen lagos, que todos deben estar en el mismo color. Este es entonces adicional a cualquier color que se requieren para las regiones políticas. Si los lagos se cuentan como una sola región, el teorema no se aplica. Puede ser aplicado a áreas de tierra del mapa solo considerando los lagos como no perteneciente a las regiones de mapa, pero en los mapas reales varios no regiones mapa contiguos pueden pertenecer además a un único no conectada región política y requieren el mismo color (ver más abajo ), por lo que, de nuevo el teorema no se aplica.
Los libros de texto sobre la cartografía y la historia de la cartografía no mencionan el teorema de los cuatro colores, a pesar mapa colorante es un tema de discusión. En general, los cartógrafos dicen que están más preocupados por la coloración de los mapas políticos de una manera equilibrada, por lo que no hay color único domina. Ya sea que se utilizan cuatro, cinco, o más colores no es una preocupación primordial.
Declaración formal en la teoría de grafos
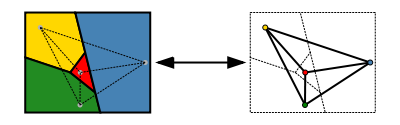
Para declarar formalmente el teorema, es más fácil de reformularla en la teoría de grafos. A continuación, señala que el vértices de cada grafo plano puede ser coloreada con un máximo de cuatro colores de modo que no hay dos vértices adyacentes reciben el mismo color. O "cada grafo plano es de cuatro plausible" para abreviar. Aquí, cada región del mapa se sustituye por un vértice de la gráfica, y dos vértices están conectados por una borde si y sólo si las dos regiones comparten un segmento de borde (no sólo una esquina).
Refutaciones falsos
Al igual que muchos problemas abiertos famosos de las matemáticas, el teorema de los cuatro colores ha atraído a un gran número de falsas pruebas y refutaciones en su larga historia. Algunos, como Kempe de Tait y del mencionado anteriormente, se puso bajo el escrutinio público durante más de una década antes de que fueran expuestas. Pero muchos más, escrito por los aficionados, nunca fueron publicadas en absoluto.
 |  |
| Este mapa se ha coloreado con cinco colores ... | ... Pero es necesario cambiar al menos cuatro de las diez regiones para obtener una coloración con sólo cuatro colores. |
En general, el "contraejemplos" intento más sencilla de crear una región que toca todas las demás regiones. Esto obliga a las demás regiones a ser de color con sólo tres colores. Debido a que el teorema de los cuatro colores es verdad, esto es siempre posible; sin embargo, porque la persona dibujar el mapa se centra en la región grande, no se dan cuenta de que las regiones restantes pueden de hecho ser coloreados con tres colores.
Este truco se puede generalizar: hay muchos mapas en la que si se seleccionan los colores de algunas regiones de antemano, se hace imposible para colorear las regiones restantes sin exceder de cuatro colores. Un verificador casual del contraejemplo puede no pensará en cambiar los colores de estas regiones, por lo que el contraejemplo aparecerá como si es válida.
Quizás uno de los efectos que subyace a este error común es el hecho de que la restricción de color no es transitiva: una región sólo tiene que ser de color diferente a las regiones lo que toca directamente, no a regiones que tocan regiones que toca. Si esto fuera la restricción, grafos planos requerirían arbitrariamente un gran número de colores.
Otros refutaciones falsas violan los supuestos del teorema de maneras inesperadas, tales como el uso de una región que consiste en múltiples partes desconectadas, o no permitir regiones del mismo color se toquen en un punto.
Las generalizaciones
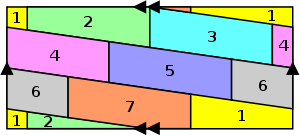
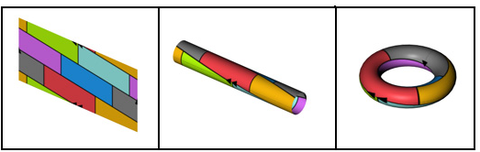
Uno puede también considerar el problema de la coloración sobre superficies que no sean el avión . El problema en la esfera o cilindro es equivalente a que en el plano. Por cerrado (orientable o no orientable) superficies con positivo género, el número p máximo de colores necesarios depende de la superficie característica de Euler χ acuerdo con la fórmula
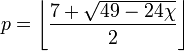 ,
,
donde los corchetes denotan la ultraperiféricas la función del suelo. La única excepción a la fórmula es la botella de Klein , que tiene característica de Euler 0 y requiere 6 colores. Esto fue conocido inicialmente como el Conjetura Heawood y demostrado como El color de mapa Teorema por Gerhard Ringel y JTW Youngs en 1968.
Alternativamente, para una superficie orientable la fórmula puede ser dada en términos de la género de una superficie, g:
Por ejemplo, el toro tiene característica de Euler χ = 0 (y género g = 1) y por lo tanto p = 7, por lo que no se requieren más de 7 colores para colorear cualquier mapa de un toro.
La Cinta de Moebius también requiere seis colores.
No hay extensión útil del problema de coloración a las regiones sólidos tridimensionales. Es trivial para construir un conjunto de n varillas flexibles, por ejemplo, de tal manera que cada varilla toca cada otra varilla. El conjunto requeriría entonces n colores, o n + 1 si se tiene en cuenta el espacio vacío que también toca cada varilla. n puede ser tomado como un entero, tan grande como se desee.
Regiones no contiguas
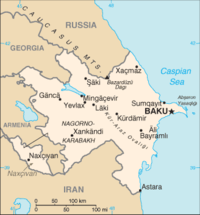
En el mundo real, no todos los países son contiguos (por ejemplo, Alaska como parte de la de Estados Unidos , Najicheván como parte de Azerbaiyán , y Kaliningrado como parte de Rusia ). Si el esquema de color elegido requiere que el territorio de un país en particular debe ser del mismo color, cuatro colores pueden no ser suficientes. Por ejemplo, considere un mapa simplificado:
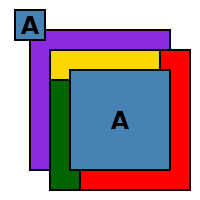
En este mapa, las dos regiones marcadas A pertenecen a un mismo país, y debe ser el mismo color. Este mapa se requiere de cinco colores, ya que las dos regiones A juntos son contiguas a otras cuatro regiones, cada una de las cuales es contigua a todos los demás. Si A consistió en tres regiones, podrían ser necesarios seis o más colores; uno puede construir mapas que requieren un número arbitrariamente alto de colores.