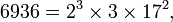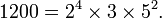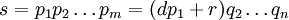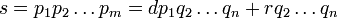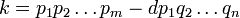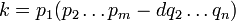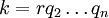Teorema fundamental de la aritmética
Sabías ...
SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Infantil SOS es la mayor donación de caridad del mundo niños huérfanos y abandonados de la oportunidad de la vida familiar.
En la teoría de números , el teorema fundamental de la aritmética (o teorema única-prime-factorización) establece que cada número natural mayor que 1 puede escribirse como un producto único de los números primos . Por ejemplo,
No hay otras posibles factorizaciones de 6936 o 1200 en números primos. La representación anterior repetidos colapsos factores primos en poderes para facilitar la identificación. Debido a que la multiplicación es conmutativa y asociativa , el orden de los factores no es relevante y por lo general por escrito de menor a mayor.
Muchos autores toman los números naturales para comenzar con 0, que no tiene factores primos. Así teorema 1 de Hardy y Wright (1979) toma la forma: "Cada entero positivo, excepto 1, es un producto de números primos", y el Teorema 2 (su "Fundamental") afirma singularidad. El número 1 no es en sí es de primera, pero ya que es el producto de ningún número, a menudo es conveniente incluirlo en el teorema por el regla del producto vacío. (Véase, por ejemplo, Cálculo de la GCD ).
Hardy y Wright definen un número anormal de ser un número hipotético de que no tiene una factorización prima única. Prueban el teorema fundamental de la aritmética, demostrando que no existe un número anormal.
Aplicaciones
El teorema fundamental de la aritmética establece la importancia de los números primos. Los números primos son los pilares básicos de cualquier número entero positivo, en el sentido de que cada número entero positivo se puede construir a partir del producto de primos con una construcción única. Encontrar la descomposición en factores primos de un entero permite la derivación de todos sus divisores, tanto de primera y segunda calidad.
Por ejemplo, la factorización anterior de 6936 muestra que cualquier divisor positivo de 6936 debe tener la forma 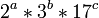 , Donde
, Donde 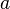 toma uno de los valores 4 en {0, 1, 2, 3}, donde
toma uno de los valores 4 en {0, 1, 2, 3}, donde 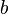 toma uno de los valores 2 en {0, 1}, y donde
toma uno de los valores 2 en {0, 1}, y donde  toma uno de los valores 3 en {0, 1, 2}. Multiplicando el número de opciones independientes entre sí produce un total de
toma uno de los valores 3 en {0, 1, 2}. Multiplicando el número de opciones independientes entre sí produce un total de 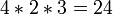 divisores positivos.
divisores positivos.
Una vez que se conocen los factores primos de dos números, su máximo común divisor y el mínimo común múltiplo se puede encontrar de forma rápida. Por ejemplo, a partir de lo anterior se demuestra que el máximo común divisor de 6936 y 1200 es 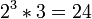 . Sin embargo, si no se conocen los factores primos, el uso de la Euclidiana algoritmo general requiere mucho menos cálculo de factoring los dos números.
. Sin embargo, si no se conocen los factores primos, el uso de la Euclidiana algoritmo general requiere mucho menos cálculo de factoring los dos números.
El teorema fundamental que asegura aditivo y multiplicativo funciones aritméticas están totalmente determinados por sus valores sobre los poderes de los números primos.
Prueba
El teorema fue prácticamente demostrado por Euclides , pero la primera prueba completa y correcta se encuentra en el Disquisitiones Arithmeticae por Carl Friedrich Gauss . Puede ser importante tener en cuenta que los egipcios gusta Ahmes usa aspectos anteriormente prácticos del factoring, y más bajo común múltiplo, del teorema fundamental de la aritmética que permite una larga tradición de desarrollar, formalizado por Euclides, y rigurosamente probada por Gauss.
Aunque a primera vista el teorema parece "obvio", no lleva a cabo en los sistemas de numeración más generales, incluyendo muchos anillos de enteros algebraicos. Así lo señaló en primer lugar por Ernst Kummer en 1843, en su obra sobre el último teorema de Fermat . El reconocimiento de este fracaso es uno de los primeros desarrollos en teoría algebraica de números.
La demostración de Euclides
La prueba consta de dos pasos. En el primer paso se muestra cada número a ser un producto de cero o más números primos. En la segunda, la prueba muestra que dos representaciones pueden unificarse en una sola representación.
Números compuestos no prime
Supongamos que hubiera un número entero positivo que no puede ser escrito como un producto de números primos. Entonces debe haber un tal número más pequeño (ver bien-orden): deja que sea n. Este número n no puede ser 1, debido a la convención-vacío producto anteriormente. No puede ser un número primo o bien, ya que cualquier número primo es un producto de una sola prima, sí. Por lo tanto, debe ser un número compuesto. Así
- n = ab
donde tanto a como b son números enteros positivos menor que n. Puesto que n es el número más pequeño que no puede ser escrito como un producto de números primos, ambos a y b pueden ser escritas como productos de números primos. Pero entonces
- n = ab
puede ser escrito como un producto de números primos, así, una prueba por la contradicción. Esto es un argumento mínimo contraejemplo.
Descenso infinito
Una prueba de la unicidad de la factorización prima de un determinado usos enteros descenso infinito: Supongamos que un cierto número entero se puede escribir como (al menos) dos diferentes productos de números primos: entonces debe existir un número entero más pequeño  con este tipo de propiedad. Denotemos estos dos factorizaciones de
con este tipo de propiedad. Denotemos estos dos factorizaciones de  como
como 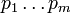 y
y 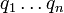 , De tal manera que
, De tal manera que 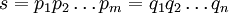 .
.
No 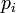 (Con
(Con 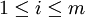 ) Puede ser igual a cualquier
) Puede ser igual a cualquier 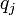 (Con
(Con 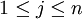 ), Ya que de otro modo sería un número entero menor factorizable de dos maneras (mediante la eliminación de los factores primos comunes en ambos productos), violando el supuesto anterior. Ahora se puede suponer sin pérdida de generalidad que
), Ya que de otro modo sería un número entero menor factorizable de dos maneras (mediante la eliminación de los factores primos comunes en ambos productos), violando el supuesto anterior. Ahora se puede suponer sin pérdida de generalidad que 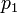 es un factor primo más pequeño que cualquier
es un factor primo más pequeño que cualquier 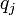 (Con
(Con 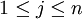 ). Dejar
). Dejar 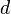 ser el cociente y
ser el cociente y  la resto de dividir
la resto de dividir 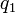 por
por 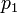 . Por el algoritmo de la división
. Por el algoritmo de la división 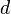 y
y  están garantizados ser números enteros tales que
están garantizados ser números enteros tales que 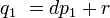 y
y 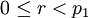 . Tenga en cuenta que
. Tenga en cuenta que  no puede ser
no puede ser 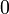 , Ya que eso haría que
, Ya que eso haría que 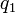 un múltiplo de
un múltiplo de 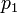 y no prime. También
y no prime. También 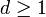 , Ya
, Ya 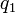 es mayor que
es mayor que 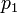 .
.
Sustituyendo en para 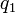 en la definición original de
en la definición original de  anteriormente,
anteriormente,
Por distributividad:
Definir un nuevo entero 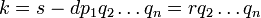 . Desde
. Desde 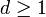 , Es claro que
, Es claro que 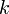 debe ser menor que
debe ser menor que  . Y desde
. Y desde 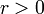 ,
, 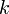 debe ser positivo. De la definición de
debe ser positivo. De la definición de 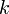 , Se deduce que:
, Se deduce que:
y al factorizar el 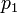 :
:
Por lo tanto hay una factorización prima de 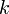 eso incluye
eso incluye 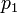 . Pero también es cierto que
. Pero también es cierto que
Desde 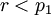 ,
, 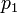 no puede ser un factor primordial de
no puede ser un factor primordial de  . Por lo tanto, mediante la combinación de los factores primos de
. Por lo tanto, mediante la combinación de los factores primos de  con
con 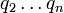 , También es posible construir una factorización prima de
, También es posible construir una factorización prima de 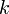 que no incluye
que no incluye 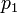 . Por lo tanto
. Por lo tanto 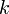 tiene dos factores primos diferentes, contradiciendo la suposición original que
tiene dos factores primos diferentes, contradiciendo la suposición original que  es la factorizable menor entero en más de una forma. Así, el supuesto original debe ser falsa.
es la factorizable menor entero en más de una forma. Así, el supuesto original debe ser falsa.