Teoría del juego
Acerca de este escuelas selección Wikipedia
SOS Children, una organización benéfica educación , organizó esta selección. Una buena manera de ayudar a otros niños es mediante el patrocinio de un niño
| Ciencias económicas |
|---|
 Economías por país |
| Clasificaciones generales |
|
| Métodos técnicos |
|
| Los campos y subcampos |
|
| Listas |
|
|
Portal de negocios y economía | La teoría de juegos está incluido en el JEL códigos de clasificación: JEL: C7 |
La teoría de juegos es un estudio de la estratégica toma de decisiones. Más formalmente, es "el estudio de modelos matemáticos de los conflictos y la cooperación entre los tomadores de decisiones racionales inteligentes. "Un término alternativo sugirieron" como un nombre más descriptivo para la disciplina "es interactivo teoría de la decisión. La teoría de juegos se utiliza principalmente en la economía, la ciencia política y la psicología, así como la lógica y la biología. El tema abordado primero juegos de suma cero, pérdidas netas de ganancias de tal manera que una persona exactamente iguales de otro participante (s). Hoy, sin embargo, la teoría de juegos se aplica a una amplia gama de relaciones de clase, y se ha convertido en un término general para el lado lógico de la ciencia, para incluir tanto los no-humanos y humanos, como las computadoras. Usos clásicos incluyen un sentido de equilibrio en numerosos juegos, en la que cada persona se ha encontrado o desarrollado una táctica que no pueden con éxito mejor sus resultados, dado el otro enfoque.
La teoría de juegos moderna comenzó con la idea de la existencia de equilibrios en estrategias mixtas en dos personas juegos de suma cero y su prueba por John von Neumann . Prueba original de Von Neumann utiliza Teorema del punto fijo de Brouwer en aplicaciones continuas en conjuntos convexos compactos, que se convirtió en un método estándar en la teoría de juegos y la economía matemática. Su papel fue seguido por su libro 1944 Teoría de Juegos y Comportamiento Económico, con Oskar Morgenstern, que considera los juegos cooperativos de varios jugadores. La segunda edición de este libro proporciona una teoría axiomática de la utilidad esperada, lo que permitió a los estadísticos matemáticos y economistas para tratar la toma de decisiones en condiciones de incertidumbre.
Esta teoría fue desarrollada ampliamente en la década de 1950 por muchos estudiosos. La teoría de juegos se aplicó más tarde explícitamente a la biología en la década de 1970, a pesar de una evolución similar se remontan al menos hasta el 1930. La teoría de juegos ha sido ampliamente reconocido como una herramienta importante en muchos campos. Ocho juego-teóricos han ganado el Premio Nobel de Economía, y John Maynard Smith fue galardonado con el Premio Crafoord por su aplicación de la teoría de juegos a la biología.
Representación de juegos
Los juegos estudiados en la teoría de juegos son objetos matemáticos bien definidos. Un juego consiste en un conjunto de jugadores, un conjunto de movimientos (o estrategias) a disposición de los jugadores, y una especificación de pagos para cada combinación de estrategias. La mayoría de los juegos cooperativos son presentados en forma de función característica, mientras que la extensa y las formas normales se utilizan para definir los juegos no cooperativos.
Forma extensiva
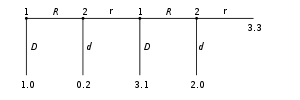
La forma extensa puede ser utilizado para formalizar juegos con una secuencia temporal de movimientos. Acción aquí se juegan en árboles (como se muestra a la izquierda). Aquí cada vértice (o nodo) representa un punto de elección para un jugador. El jugador se especifica por un número que se indica por el vértice. Las líneas de cada vértice representan una posible acción para ese jugador. Los pagos se especifican en la parte inferior del árbol. La forma extensa puede ser visto como un multi-jugador generalización de una árbol de decisión. (Fudenberg y Tirole 1991, p. 67)
En el juego se muestra a la izquierda, hay dos jugadores. El jugador 1 mueve primero y elige F o U. Jugador 2 ve movimiento del jugador 1 's y luego elige A o R. Supongamos que el jugador 1 elige U y entonces el jugador 2 elige A, entonces el jugador 1 obtiene 8 y el jugador 2 obtiene 2.
La forma extensiva también puede capturar juegos simultánea-movimiento y juegos con información imperfecta. Para representarlo, ya sea una línea de puntos conecta diferentes vértices para representarlos como formando parte de la misma información que figura (es decir, los jugadores no saben en qué punto lo son), o una línea cerrada se dibuja alrededor de ellos. (Véase el ejemplo en la sección de información imperfecta .)
Forma normal
| Jugador 2 elige Izquierda | Jugador 2 elige Derecho | |
| Jugador 1 elige Hasta | 4, 3 | -1, -1 |
| Jugador 1 elige Abajo | 0, 0 | 3, 4 |
| Forma o recompensa normal matriz de un 2-jugador, juego 2-estrategia | ||
El (forma o estratégicos) de juego normal se suele representar por una matriz que muestra a los jugadores, estrategias, y pagar compensaciones (ver el ejemplo de la derecha). Más generalmente se puede representar por cualquier función que asocia un pago por cada jugador con cada combinación posible de acciones. En el ejemplo adjunto hay dos jugadores; uno elige la fila y el otro elige la columna. Cada jugador tiene dos estrategias, que se especifican por el número de filas y el número de columnas. Los beneficios se proporcionan en el interior. El primer número es la recompensa recibida por el jugador de la primera (Jugador 1 en nuestro ejemplo); el segundo es la recompensa para el jugador columna (jugador 2 en nuestro ejemplo). Supongamos que el jugador 1 juega Arriba y ese jugador 2 juega Izquierda. Entonces el jugador 1 recibe un pago de 4, y el jugador 2 consigue 3.
Cuando un juego se presenta en forma normal, se supone que cada jugador actúa simultáneamente o, al menos, sin conocer las acciones de la otra. Si los jugadores tienen alguna información acerca de las opciones de los otros jugadores, el juego está por lo general se presenta en forma extensiva.
Cada forma extensiva juego tiene un juego en forma normal equivalente, sin embargo, la transformación en forma normal puede resultar en una explosión exponencial en el tamaño de la representación, por lo que es computacionalmente poco práctico. (Leyton-Brown & Shoham 2008, p. 35)
Forma de función característica
En los juegos que poseen utilidad extraíble no se dan recompensas por separado; más bien, la función característica decide la rentabilidad de cada unidad. La idea es que la unidad que es "vacío", por así decirlo, no recibe una recompensa en absoluto.
El origen de esta forma se encuentra en John von Neumann y Oskar Morgenstern libro de; cuando se mira en estos casos, se supuso que cuando un sindicato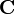 
aparece, va en contra de la fracción 
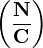como si dos personas estaban jugando un juego normal. La recompensa equilibrada de C es una función básica. Aunque existen diferentes ejemplos que ayudan a determinar las cantidades de coalición de los juegos normales, no todo parece que en su forma de función se puede derivar de tales.
Formalmente, una función característica es visto como: (N, v), donde N representa el grupo de personas y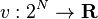 
es una utilidad normal.
Tales funciones características se han ampliado para describir los juegos donde no hay utilidad extraíble.
Forma de función de partición
La forma de función característica ignora la posible externalidades de la formación de coaliciones. En la función de partición forman la recompensa de una coalición no sólo depende de sus miembros, sino también de la forma en que el resto de los jugadores se reparte (Thrall & Lucas 1963).
General y usos aplicados
Como un método de matemática aplicada , la teoría de juegos ha sido utilizado para estudiar una amplia variedad de comportamientos humanos y animales. Fue desarrollado inicialmente en economía para entender una gran colección de los comportamientos económicos, incluidos los comportamientos de las empresas, los mercados y los consumidores. El uso de la teoría de juegos en las ciencias sociales se ha expandido, y la teoría de juegos se ha aplicado a los comportamientos políticos, sociológicos y psicológicos.
Análisis Juego-teórico se utilizó inicialmente para estudiar el comportamiento animal por Ronald Fisher en la década de 1930 (aunque incluso Charles Darwin hace algunas declaraciones de teoría de juegos informales). Este trabajo es anterior el nombre de "teoría de juegos", pero comparte muchas características importantes con este campo. Los avances en la economía más tarde se aplicaron a la biología en gran parte por John Maynard Smith en su libro Evolución y la Teoría de Juegos.
Además de ser utilizado para describir, predecir y explicar el comportamiento, la teoría de juegos también se ha utilizado para desarrollar teorías de comportamiento ético o normativo ya prescribir este tipo de comportamiento. En economía y filosofía, los estudiosos han aplicado la teoría de juegos para ayudar en la comprensión de la conducta buena o adecuada. Argumentos de la teoría de los juegos de este tipo se pueden encontrar ya en Platón .
Descripción y modelado
El primer uso conocido es describir y modelo de cómo las poblaciones humanas se comportan. Algunos estudiosos creen que mediante la búsqueda de los equilibrios de juegos que pueden predecir cómo las poblaciones humanas reales se comportan cuando se enfrentan a situaciones análogas a la partida que se está estudiando. Este punto de vista particular de la teoría de juegos ha sido objeto de críticas recientes. En primer lugar, se critica porque las suposiciones hechas por los teóricos del juego son a menudo violados. Los teóricos de juegos pueden asumir los jugadores siempre actúan de una manera de maximizar directamente sus victorias (la Modelo de homo economicus), pero en la práctica, el comportamiento humano a menudo se desvía de este modelo. Las explicaciones de este fenómeno son muchas; irracionalidad, nuevos modelos de deliberación, o incluso diferentes motivos (como la del altruismo ). Los teóricos de juegos responden mediante la comparación de sus supuestos a los que se utilizan en la física. Así, aunque sus supuestos no siempre se mantienen, pueden tratar la teoría de juegos como un científico razonable semejante ideal para los modelos utilizados por los físicos. Sin embargo, en el juego del ciempiés, adivinar 2/3 de la media de juego, y el juego del dictador, la gente regularmente no juego equilibrios de Nash. Estos experimentos han demostrado que las personas no juegan estrategias de equilibrio. Hay un debate en curso sobre la importancia de estos experimentos.
Por otra parte, algunos autores afirman que los equilibrios de Nash no proporcionan predicciones para las poblaciones humanas, sino más bien una explicación de por qué las poblaciones que desempeñan los equilibrios de Nash permanecen en ese estado. Sin embargo, la cuestión de cómo las poblaciones alcancen esos puntos se mantiene abierto.
Algunos teóricos de juegos han recurrido a la teoría de juegos evolutiva con el fin de resolver estos problemas. Estos modelos suponen bien hay racionalidad o racionalidad limitada por parte de los jugadores. A pesar del nombre, la teoría de juegos evolutiva no supone necesariamente la selección natural en el sentido biológico. La teoría de juegos evolutiva incluye tanto biológicos, así como la evolución cultural y también los modelos de aprendizaje individual (por ejemplo, la dinámica de juego ficticio).
Análisis prescriptivo o normativo
| Cooperar | Defecto | |
| Cooperar | -1, -1 | -10, 0 |
| Defecto | 0, -10 | -5, -5 |
| El dilema del prisionero | ||
Por otro lado, algunos estudiosos ven no como teoría de juegos una herramienta de predicción del comportamiento de los seres humanos, sino como una sugerencia de cómo hay que comportarse. Desde una estrategia, que corresponde a un equilibrio de Nash de un juego constituye uno de mejor respuesta a las acciones de los otros jugadores - siempre que hayan sido (lo mismo) el equilibrio de Nash -, jugando una estrategia que forma parte de un equilibrio de Nash parece apropiado. Sin embargo, la racionalidad de una decisión de este tipo se ha probado sólo en casos especiales. Este uso normativo de la teoría del juego también ha sido objeto de críticas. En primer lugar, en algunos casos es apropiado para jugar una estrategia de no equilibrio si se espera que otros jueguen estrategias de no-equilibrio también. Para ver un ejemplo, consulte adivinar 2/3 de la media.
En segundo lugar, la dilema del prisionero presenta otro contraejemplo potencial. En el dilema del prisionero, cada jugador persigue su propio interés conduce a ambos jugadores a ser peor que si no hubieran seguido adelante con sus propios intereses.
Economía y negocios
La teoría de juegos es un método principal que se utiliza en economía matemática y las empresas para modelar comportamientos competitivos de la interacción agentes. Las aplicaciones incluyen una amplia gama de fenómenos y enfoques económicos, tales como subastas, la negociación, fusiones y adquisiciones de precios, división justa, duopolios, oligopolios, social, formación de redes, economía computacional basada en agentes, equilibrio general, diseño de mecanismos, y sistemas de votación, ya través de campos tan amplios como economía experimental, la economía del comportamiento , economía de la información, organización industrial y economía política .
Esta investigación se centra generalmente en conjuntos particulares de estrategias conocidos como equilibrios en juegos. Estos "conceptos de solución" generalmente se basan en lo que se requiere por las normas de racionalidad. En los juegos no cooperativos, el más famoso de ellos es el equilibrio de Nash . Un conjunto de estrategias es un equilibrio de Nash si cada uno representa una mejor respuesta a las otras estrategias. Así que, si todos los jugadores están jugando las estrategias en un equilibrio de Nash, no tienen ningún incentivo para desviarse unilateral, ya que su estrategia es la mejor que pueden hacer teniendo en cuenta lo que otros están haciendo.
Los beneficios del juego se toman generalmente para representar el utilidad de los jugadores individuales. A menudo, en situaciones de modelado los pagos representan dinero, que presumiblemente corresponde a la utilidad de un individuo. Esta hipótesis, sin embargo, puede estar defectuoso.
Un papel prototípico en la teoría de juegos en economía comienza presentando un juego que es una abstracción de una situación económica particular. Uno o más conceptos de solución se eligen, y el autor demuestra que los conjuntos de estrategias en el juego presentado son los equilibrios del tipo apropiado. Naturalmente cabe preguntarse a qué uso se debe poner esta información. Los economistas y profesores de negocios sugieren dos usos primarios (mencionados anteriormente): descriptivo y prescriptivo.
Ciencias Políticas
La aplicación de la teoría de juegos a la ciencia política se centra en las áreas de solapamiento de división justa, la economía política , la elección pública, negociación guerra, teoría política positiva, y teoría de la elección social. En cada una de estas áreas, los investigadores han desarrollado modelos de teoría de juegos en el que los jugadores son a menudo los votantes, estados, grupos de intereses especiales, y los políticos.
Para los primeros ejemplos de la teoría de juegos aplicada a la ciencia política, ver el trabajo de Anthony Downs. En su libro Una Teoría Económica de la Democracia (Downs 1957), que se aplica la Hotelling modelo situación firme al proceso político. En el modelo downsiano, candidatos políticos se comprometen a ideologías en un espacio político unidimensional. Downs primero muestra cómo los candidatos políticos se reunirán con la ideología preferida por el votante medio si los votantes están plenamente informados, pero sostiene que los votantes eligen permanecer racionalmente ignorantes que permite la divergencia candidato.
Una explicación de teoría de juegos para paz democrática es que el debate público y abierto en las democracias enviar información clara y fiable sobre sus intenciones a otros estados. Por el contrario, es difícil saber las intenciones de los dirigentes no democráticos, lo tendrán concesiones efecto, y si se mantendrá promesas. Por lo tanto, habrá desconfianza y falta de voluntad para hacer concesiones si al menos una de las partes en una controversia es un no-democracia (Levy y Razin 2003).
Biología
| Halcón | Paloma | |
| Halcón | 20, 20 | 80, 40 |
| Paloma | 40, 80 | 60, 60 |
| El juego del halcón-paloma | ||
Los beneficios para los juegos en la biología , a diferencia de los de la economía, a menudo se interpretan como correspondiente a gimnasio. Además, el enfoque ha sido menos en equilibrios que corresponden a una noción de racionalidad y más en los que se mantienen por evolutivos fuerzas. El equilibrio más conocido en biología se conoce como la estrategia evolutivamente estable (o ESS), y se introdujo por primera vez en (Smith & Precio 1.973). Aunque su motivación inicial no recurra a ninguno de los requisitos mentales del equilibrio de Nash , cada EEE es un equilibrio de Nash.
En biología, la teoría de juegos se ha utilizado para entender muchos fenómenos diferentes. Fue utilizado por primera vez para explicar la evolución (y estabilidad) de los aproximadamente 1: 1 la proporción de sexos. (Fisher 1930) sugirió que los 1: 1 proporción de sexos son el resultado de fuerzas evolutivas que actúan sobre las personas que podrían considerarse como tratando de maximizar el número de sus nietos.
Además, los biólogos han utilizado la teoría de juegos evolutiva y el SEE para explicar la aparición de la comunicación animal (Harper & Maynard Smith, 2003). El análisis de juegos de señalización y otros de comunicación ha proporcionado información sobre la evolución de la comunicación entre los animales. Por ejemplo, el mobbing comportamiento de muchas especies, en la que un gran número de animales de presa atacar a un depredador más grande, que parece ser un ejemplo de organización emergente espontánea. Las hormigas también han demostrado exhibir un comportamiento de alimentación hacia adelante similar a la moda, ver Economía de la mariposa.
Los biólogos han utilizado el juego de la gallina para analizar el comportamiento de la lucha y la territorialidad.
Maynard Smith, en el prefacio de la Evolución y la Teoría de Juegos, escribe, "paradójicamente, se ha puesto de manifiesto que la teoría de juegos se aplica más fácilmente a la biología que en el campo del comportamiento económico para el que fue diseñado originalmente". La teoría de juegos evolutiva se ha utilizado para explicar muchos fenómenos aparentemente incongruentes en la naturaleza.
Uno de tales fenómeno se conoce como altruismo biológico. Esta es una situación en la que un organismo parece actuar de una manera que beneficia a otros organismos y es perjudicial para sí mismo. Esto es distinto de las nociones tradicionales de altruismo, porque este tipo de acciones no son conscientes, pero parecen ser adaptaciones evolutivas para aumentar la condición física general. Se pueden encontrar ejemplos de especies que van desde los vampiros que regurgitan sangre que han obtenido de la caza de una noche y le dan a los miembros del grupo que no han podido alimentar a las abejas obreras que cuidan de la abeja reina durante toda su vida y nunca se aparean, a monos verdes que advierten los miembros del grupo de enfoque de un depredador, incluso cuando se pone en peligro la posibilidad de que la persona de la supervivencia. Todas estas acciones aumentan el estado físico general de un grupo, pero se producen a un costo para el individuo.
La teoría de juegos evolutiva explica este altruismo con la idea de la selección de parentesco. Los altruistas discriminar entre los individuos que ayudan y parientes favor. La regla de Hamilton explica el razonamiento detrás de esta selección evolutiva con la ecuación c La teoría de juegos ha pasado a desempeñar un papel cada vez más importante en la lógica y en ciencias de la computación . Varias teorías lógicas tienen una base en semántica de juego. Además, los informáticos han utilizado juegos para modelar cálculos interactivos. Además, la teoría de juegos proporciona una base teórica para el campo de la sistemas multiagente. Por otra parte, la teoría de juegos ha jugado un papel en la algoritmos en línea. En particular, la problema k-servidor, que en el pasado ha sido referido como juegos con costos de mudanza y juegos solicitud de respuesta (Ben David, Borodin y Karp et al. 1994). Principio de Yao es una técnica de teoría de juegos para demostrar cotas inferiores de la complejidad computacional de aleatorizado algoritmos, y especialmente de los algoritmos en línea. La aparición de Internet ha motivado el desarrollo de algoritmos para la búsqueda de equilibrios en los juegos, los mercados, las subastas de cómputo, sistemas peer-to-peer, y los mercados de seguridad y de información. La teoría de juegos algorítmica y dentro de ella diseño de mecanismos algorítmica combinar computacional diseño de algoritmos y análisis de sistemas complejos con la teoría económica. La teoría de juegos ha sido objeto de varios usos en la filosofía . En respuesta a dos documentos por WVO Quine (1960, 1967), Lewis (1969) utilizó la teoría de juegos para desarrollar una explicación filosófica de convención. Al hacerlo, él proporcionó el primer análisis de conocimiento común y lo empleó en el análisis de juego en juegos de coordinación. Además, se sugirió por primera vez que se puede entender lo que significa en términos de señalización juegos. Esta sugerencia más tarde ha sido perseguido por varios filósofos desde Lewis (Skyrms (1996), Grim, Kokalis, y Alai-Tafti et al. (2004)). Después de Lewis (1969) cuenta la teoría de juegos de convenciones, Edna Ullmann-Margalit (1977) y Bicchieri (2006) han desarrollado teorías de normas sociales que las definen como los equilibrios de Nash que resultan de la transformación de un juego mixto-motriz en un juego de coordinación. La teoría de juegos también ha desafiado a los filósofos a pensar en términos de interactivo epistemología: lo que significa para un colectivo que tiene creencias o conocimientos comunes, y cuáles son las consecuencias de este conocimiento para los resultados sociales que resultan de las interacciones de los agentes. Los filósofos que han trabajado en esta área incluyen Bicchieri (1989, 1993), Skyrms (1990), y Stalnaker (1999). En la ética , algunos autores han tratado de continuar con el proyecto, iniciado por Thomas Hobbes , de la moral que deriva de su propio interés. Desde juegos como el dilema del prisionero presenta un aparente conflicto entre la moral y el interés propio, lo que explica por qué se requiere la cooperación por el interés propio es un componente importante de este proyecto. Esta estrategia general es un componente de la general vista contrato social en la filosofía política (por ejemplo, ver Gauthier (1986) y Kavka (1986). Otros autores han intentado utilizar la teoría de juegos evolutiva para explicar el surgimiento de actitudes humanas acerca de la moral y de los comportamientos de los animales correspondientes. Estos autores examinan varios juegos, incluyendo el dilema del prisionero, caza del ciervo, y la Juego de negociación de Nash como proporcionar una explicación para la aparición de actitudes acerca de la moralidad (véase, por ejemplo, Skyrms (1996, 2004) y Sober y Wilson (1999)). Algunos supuestos utilizados en algunas partes de la teoría de juegos se han impugnado en la filosofía; por ejemplo, egoísmo psicológico afirma que la racionalidad reduce al interés propio-una reclamación debatida entre los filósofos. (Ver Egoísmo psicológico # Críticas) Un juego es cooperativo si los jugadores son capaces de formar compromisos vinculantes. Por ejemplo, el sistema legal les obliga a cumplir con sus promesas. En los juegos no cooperativos esto no es posible. A menudo se asume que se permite la comunicación entre los jugadores en los juegos cooperativos, pero no en los no cooperativos. Sin embargo, esta clasificación en dos criterios binarios ha sido cuestionada, ya veces rechazado (Harsanyi 1974). De los dos tipos de juegos, los juegos no cooperativos son capaces de modelar situaciones para los detalles más finos, produciendo resultados precisos. Juegos cooperativos se centran en el juego en general. Se han hecho esfuerzos considerables para vincular los dos enfoques. El llamado Nash-programa ya ha establecido muchas de las soluciones cooperativas como equilibrios no cooperativos. Juegos híbridos contienen elementos cooperativos y no cooperativos. Por ejemplo, las coaliciones de los jugadores se forman en un juegos cooperativos, pero estos desempeñan en forma no cooperativa. Un juego simétrico es un juego donde los beneficios para la reproducción de una estrategia en particular dependen sólo de las otras estrategias empleadas, no de quién está jugando con ellos. Si las identidades de los jugadores pueden ser cambiados sin cambiar la recompensa a las estrategias, a continuación, un juego es simétrica. Muchos de los comúnmente estudiados 2 × 2 juegos son simétricas. Las representaciones estándar de pollo, la dilema del prisionero, y la caza del ciervo son todos los juegos simétricos. Algunos estudiosos considerarían ciertos juegos asimétricos como ejemplos de estos juegos también. Sin embargo, los beneficios más comunes para cada uno de estos juegos son simétricas. Más comúnmente juegos asimétricos estudiados son juegos donde no hay conjuntos de estrategias idénticas para ambos jugadores. Por ejemplo, el juego del ultimátum y de manera similar la juego del dictador tienen diferentes estrategias para cada jugador. Es posible, sin embargo, para un juego de disponer de estrategias idénticas para ambos jugadores, sin embargo, ser asimétrica. Por ejemplo, el juego muestra a la derecha es asimétrico a pesar de tener conjuntos de estrategias idénticas para ambos jugadores. Juegos de suma cero son un caso especial de juegos de suma constante, en el que las decisiones de los jugadores no pueden aumentar ni disminuir los recursos disponibles. En los juegos de suma cero, el beneficio total a todos los jugadores en el juego, para cada combinación de estrategias, siempre añade a cero (de manera más informal, los beneficios de un jugador sólo a expensas igual de otros). Poker es un ejemplo de un juego de suma cero (ignorando la posibilidad de corte de la casa), porque uno gana exactamente la cantidad a los adversarios pierden. Otros juegos de suma cero incluyen juego peniques y la mayoría de los juegos de mesa clásicos incluyendo Go y ajedrez . Muchos de los juegos estudiados por los teóricos del juego (incluyendo el infame dilema del prisionero) son juegos que no son de suma cero, porque el resultado tiene resultados netos mayor o menor que cero. De manera informal, en juegos que no son de suma cero, una ganancia de un jugador no se corresponde necesariamente con una pérdida por otro. Juegos de suma constante corresponden a actividades como el robo y el juego, pero no a la situación económica fundamental en el que hay potencial las ganancias del comercio. Es posible transformar cualquier juego en un (posiblemente asimétrica) juego de suma cero añadiendo un jugador ficticio adicional (a menudo llamado "la junta"), cuyas pérdidas compensar las ganancias netas de los jugadores. Juegos simultáneos son juegos donde ambos jugadores se mueven simultáneamente, o si no se mueven al mismo tiempo, los jugadores posteriores no son conscientes de las acciones de los jugadores anteriores »(haciéndolos efectivamente simultánea). Juegos secuenciales (o juegos dinámicos) son juegos donde los jugadores posteriores tienen un poco de conocimiento acerca de las acciones anteriores. Esto no tiene por qué ser información perfecta sobre todas las acciones de los jugadores anteriores; puede ser que sea muy poco conocimiento. Por ejemplo, un jugador puede saber que un reproductor anterior no realizó una acción en particular, mientras que él no sabe cuál de las otras acciones disponibles realmente lleva a cabo en el primer jugador. La diferencia entre juegos simultáneos y secuenciales se captura en las distintas representaciones descritas anteriormente. A menudo, forma normal se utiliza para representar juegos simultáneos, y forma extensiva se utiliza para representar los secuenciales. La transformación de la extensa a forma normal es una manera, lo que significa que múltiples juegos en forma extensiva corresponden a la misma forma normal. En consecuencia, las nociones de equilibrio de partidas simultáneas son insuficientes para el razonamiento sobre los juegos secuenciales; ver la perfección en subjuegos. En resumen, las diferencias entre juegos secuenciales y simultáneas son los siguientes: Un subconjunto importante de los juegos secuenciales consiste en juegos de información perfecta. Un juego es una de información perfecta si todos los jugadores conocen los movimientos previamente por todos los otros jugadores. Por lo tanto, sólo los juegos secuenciales pueden ser juegos de información perfecta porque los jugadores en partidas simultáneas no conocen las acciones de los otros jugadores. La mayoría de los juegos estudiados en la teoría de juegos son juegos de información imperfecta. Ejemplos interesantes de juegos perfecto de información incluyen el juego del ultimátum y juego del ciempiés. Juegos recreativos de juegos perfectos de información incluyen ajedrez , ir y mancala . Muchos juegos de cartas son juegos de información imperfecta, por ejemplo poker o puente del contrato. Información perfecta se confunde a menudo con información completa, que es un concepto similar. Información completa requiere que cada jugador conoce las estrategias y beneficios disponibles a los otros jugadores, pero no necesariamente las acciones tomadas. Juegos de información incompleta pueden reducirse, sin embargo, a los juegos de información imperfecta, introduciendo " se mueve por la naturaleza "(Leyton-Brown & Shoham 2008, p. 60). Juegos en los que la dificultad de encontrar una estrategia óptima se debe a la multiplicidad de posibles movimientos se llaman juegos combinatorios. Algunos ejemplos son el ajedrez y van. Los juegos que involucran información imperfecta o incompleta también pueden tener un fuerte carácter combinatorio, por ejemplo backgammon . No existe una teoría unificada abordar elementos combinatorios en juegos. Hay, sin embargo, las herramientas matemáticas que pueden resolver problemas particulares y responder a preguntas generales. Juegos de información perfecta se han estudiado en la teoría del juego combinatorio, que ha desarrollado nuevas representaciones, por ejemplo, números surreales, así como combinatoria y algebraica (y a veces no constructivas) Métodos de prueba a resolver juegos de ciertos tipos, incluidos los juegos "descabellado" que pueden dar lugar infinitamente largas secuencias de movimientos. Estos métodos abordan los juegos con mayor complejidad combinatoria que las habitualmente consideradas en tradicional (o "económica") la teoría de juegos. Un juego típico que ha sido solucionado de esta manera es hexagonal. Un campo de estudio relacionado, dibujo de teoría de la complejidad computacional, es complejidad del juego, que se ocupa de la estimación de la dificultad computacional de encontrar estrategias óptimas. Research in la inteligencia artificial se ha ocupado de los dos juegos de información perfecta e imperfecta (o incompletos) que tienen estructuras combinatorias muy complejas (como el ajedrez, ir, o backgammon) para los que no se han encontrado estrategias óptimas demostrables. Las soluciones prácticas implican heurística computacionales, como poda alfa-beta o el uso de redes neuronales artificiales formados por aprendizaje por refuerzo, que hacen juegos más manejable en la práctica la computación. Juegos, ya estudiado por los economistas y los jugadores del juego de la vida real, por lo general terminaron en un número finito de movimientos. Los matemáticos puros no son tan restringidos, y establecen los teóricos en particular juegos de estudio que duran una infinidad de movimientos, con el ganador (o otra recompensa) no se conocía hasta después de todos esos movimientos se han completado. El foco de atención es por lo general, no tanto en lo que es la mejor manera de jugar un partido de este tipo, sino simplemente de si uno o el otro jugador tiene un ganar estrategia. (Se puede demostrar, utilizando la axioma de elección, que no son juegos, incluso con información perfecta, y donde los únicos resultados son "ganar" o "perder" -por la que ninguno de los jugadores tiene una estrategia ganadora.) La existencia de este tipo de estrategias, para los juegos inteligentemente diseñado, tiene consecuencias importantes en la teoría de conjuntos descriptiva. Sin embargo Gran parte de la teoría de juegos se refiere a, juegos discretos finitos, que tienen un número finito de jugadores, movimientos, eventos, resultados, etc. Muchos conceptos pueden extenderse,. Juegos continuos permiten a los jugadores elegir una estrategia de un conjunto de estrategias continua. Por ejemplo, Competencia Cournot es típicamente modelada con las estrategias de los jugadores siendo las cantidades no negativas, incluyendo cantidades fraccionarias. Juegos diferenciales tales como el continuo persecución y evasión juego son juegos continuas en las que la evolución de las variables de estado de los jugadores se rige por ecuaciones diferenciales . El problema de encontrar una estrategia óptima en un juego diferencial está estrechamente relacionada con la la teoría de control óptimo. En particular, hay dos tipos de estrategias: las estrategias de bucle abierto se encuentran usando el Pontryagin principio del máximo, mientras que las estrategias de circuito cerrado se encuentran utilizando Método de programación dinámica de Bellman. Un caso particular de juegos diferenciales son los juegos con horizonte de tiempo aleatorio. En tales juegos, el tiempo de terminal es una variable aleatoria con una determinada distribución de probabilidad función. Por lo tanto, los jugadores maximizar el esperanza matemática de la función de coste. Se demostró que el problema de optimización modificado puede ser reformulada como un juego diferencial de descuento sobre un intervalo de tiempo infinito. Juegos con un arbitrario, pero finito, el número de jugadores a menudo se llaman n personas juegos (Luce y Raiffa 1957). La teoría de juegos evolutiva considera juegos que implica un población de los tomadores de decisiones, donde la frecuencia con la que se toma una decisión en particular puede cambiar con el tiempo en respuesta a las decisiones tomadas por todos los individuos de la población. En biología, con ello se pretende modelar (biológica) evolución , donde los organismos genéticamente programados pasan a lo largo de una parte de su programación de estrategia para su descendencia.En economía, la misma teoría se pretende captar los cambios de población, porque la gente jugar el juego muchas veces en su vida, y conscientemente (y tal vez de manera racional) estrategias de conmutación (Webb 2007). Problemas de decisión individuales con resultados estocásticos a veces se consideran "juegos de un solo jugador". Estas situaciones no se consideran juego teórico por algunos autores. Pueden ser modelados utilizando herramientas similares dentro de las disciplinas relacionadas de teoría de la decisión, la investigación de operaciones y áreas de la inteligencia artificial, sobre todo la planificación de la IA (con incertidumbre) y sistema multi-agente. Aunque estos campos pueden tener diferentes motivaciones, las matemáticas involucradas son sustancialmente la misma, por ejemplo, utilizando los procesos de toma de Markov (MDP). Resultados estocásticos también pueden modelarse en términos de la teoría de juegos mediante la adición de un jugador que actúa al azar que hace "oportunidad mueve", también conocidos como " se mueve por la naturaleza "(Osborne y Rubinstein 1994). Este jugador no se considera normalmente un tercer jugador en lo que es un juego de dos jugadores, sino que simplemente sirve para proporcionar un rollo de los dados cuando sea necesario por el juego. Para algunos problemas, diferentes enfoques de los resultados de modelos estocásticos pueden dar lugar a diferentes soluciones. Por ejemplo, la diferencia de enfoque entre PDM y la solución minimax es que este último considera el peor de los casos a través de una serie de movimientos de confrontación, en vez de razonamiento en la expectativa sobre estos movimientos dados una distribución de probabilidad fija. El enfoque minimax puede ser ventajoso en modelos estocásticos de incertidumbre no están disponibles, pero también puede estar sobreestimando eventos muy improbables (pero costosas), balanceándose de manera espectacular la estrategia en este tipo de escenarios, si se asume que un adversario puede obligar a tal evento ocurra. (Ver la teoría del cisne negro para más discusión sobre este tipo de cuestiones de modelado, en particular en lo que se refiere a la predicción y limitar las pérdidas en la banca de inversión.) También se han estudiado los modelos generales que incluyen todos los elementos de los resultados estocásticos, adversarios y observabilidad parcial o ruidoso (de movimientos por parte de otros jugadores). El " estándar de oro "es considerado como parcialmente observable juego estocástico (POSG), pero son pocos los problemas reales son computacionalmente factible en representación POSG. Estos son los juegos el juego de las cuales es el desarrollo de las normas para otro juego, el juego objetivo o tema. metajuegos tratan de maximizar el valor de la utilidad del conjunto de reglas desarrollado. La teoría de la metajuegos se relaciona con la teoría de diseño de mecanismos. El término análisis de estrategia del juego también se utiliza para referirse a un enfoque práctico desarrollado por Nigel Howard (Howard 1971) por el que una situación se enmarca como un juego estratégico en el que los interesados tratan de hacer realidad sus objetivos por medio de las opciones disponibles para ellos. Los acontecimientos posteriores han llevado a la formulación de análisis de la confrontación. Las primeras discusiones de ejemplos de juegos de dos personas tuvieron lugar mucho antes de la aparición de la teoría del juego moderno, matemático. La discusión primera conocida de la teoría de juegos se produjo en una carta escrita por James Waldegrave en 1713. En esta carta, Waldegrave proporciona una minimax solución estrategia mixta a una versión de dos personas del juego de cartas le Her. James Madison hizo lo que hoy reconocemos como un análisis de teoría de juegos de las formas en los estados se puede esperar que se comporten bajo diferentes sistemas de tributación. En su 1838 Recherches sur les principes Matemáticas de la théorie des richesses ( Investigaciones en los principios matemáticos de la teoría de la riqueza ), Antoine Augustin Cournot considera un duopolio y presenta una solución que es una versión restringida del equilibrio de Nash . El matemático danés Zeuthen demostrado que el modelo matemático tenía una estrategia ganadora utilizando teorema del punto fijo de Brouwer. En sus 1.938 libros Aplicaciones aux Jeux de Hasard y notas anteriores, Émile Borel demostraron un teorema minimax para dos personas juegos de matriz de suma cero sólo cuando la matriz de pagos era simétrica. Borel conjeturó que ocurriría no existencia de equilibrios en estrategias mixtas en dos personas juegos de suma cero, una conjetura que se demostró falsa. La teoría de juegos en realidad no existe como un campo único hasta que John von Neumann publicó un artículo en la prueba original del 1928. Von Neumann utilizado teorema del punto fijo de Brouwer en aplicaciones continuas en conjuntos convexos compactos, que se convirtió en un método estándar en la teoría de juegos y la economía matemática. Su papel fue seguido por su libro 1944 Teoría de Juegos y Comportamiento Económico . La segunda edición de este libro proporciona una teoría axiomática de utilidad, que reencarna vieja teoría de la utilidad (del dinero) de Daniel Bernoulli como disciplina independiente. La obra de Von Neumann en la teoría de juegos culminó en este libro de 1944. Esta obra fundacional contiene el método para encontrar soluciones mutuamente consistentes para dos personas juegos de suma cero. Durante el siguiente período de tiempo, el trabajo sobre la teoría de juegos fue principalmente centrado en la teoría de juegos cooperativos, que analiza las estrategias óptimas para grupos de personas, suponiendo que puedan cumplir los acuerdos entre ellos acerca de estrategias adecuadas. En 1950, la primera discusión matemática del dilema del prisionero apareció, y un experimento se llevó a cabo por los matemáticos notables Merrill M. Flood y Melvin Dresher, como parte de la investigación de la corporación RAND en la teoría de juegos. Rand persiguió a los estudios debido a posibles aplicaciones a mundial estrategia nuclear. Alrededor de este mismo tiempo, John Nash desarrolló un criterio de coherencia mutua de las estrategias de los jugadores, conocidos como equilibrio de Nash, aplicable a una variedad más amplia de juegos que el criterio propuesto por von Neumann y Morgenstern. Este equilibrio es suficientemente general para permitir el análisis de juegos no cooperativos, además de las cooperativas. La teoría de juegos experimentó una intensa actividad en la década de 1950, tiempo durante el cual los conceptos del núcleo, el juego en forma extensiva, el juego ficticio, los juegos repetidos, y se desarrollaron valor de Shapley. Además, las primeras aplicaciones de la teoría de juegos a la filosofía y la ciencia política se produjeron durante este tiempo. En 1965, Reinhard Selten introdujo su concepto de la solución de equilibrio perfecto en subjuegos, que refina aún más el equilibrio de Nash (más tarde introduciría mano temblorosa la perfección también). En 1967, John Harsanyi desarrolló los conceptos de información completa y juegos bayesianos. Nash, Selten y Harsanyi convirtieron Economía Premios Nobel en 1994 por sus contribuciones a la teoría del juego económico. En la década de 1970, la teoría de juegos se ha aplicado ampliamente en la biología , en gran parte como resultado de la obra de John Maynard Smith y su estrategia evolutivamente estable . Además, los conceptos de equilibrio correlacionado, la perfección mano temblorosa, y el conocimiento común se presentaron y analizaron. En 2005, los teóricos de juegos Thomas Schelling y Robert Aumann siguieron Nash, Selten y Harsanyi como premios Nobel. Schelling trabajó en modelos dinámicos, los primeros ejemplos de la teoría de juegos evolutiva. Aumann contribuyó más a la escuela de equilibrio, la introducción de un engrosamiento de equilibrio, equilibrio correlacionado, y el desarrollo de un amplio análisis formal de la asunción de conocimiento común y de sus consecuencias. En el año 2007, Leonid Hurwicz, junto con Eric Maskin y Roger Myerson, fue galardonado con el Premio Nobel de Economía "por haber sentado las bases de la teoría de diseño de mecanismos ". Las contribuciones de Myerson incluyen la noción de equilibrio adecuado, y un texto de posgrado importante: Teoría de Juegos, Análisis de Conflictos (Myerson 1997). Hurwicz introdujo y formalizó el concepto de compatibilidad de incentivos. La historia de vida de juego teórico y matemáticoJohn Nash se convirtió en una película biográfica, Una mente maravillosa, protagonizada porRussell Crowe, basado en el libro deSylvia Nasar. "Juegos de la teoría" y "teoría de juegos" se mencionan en la novela de ciencia ficción militar Starship Troopers por Robert A. Heinlein. En la película del mismo nombre de 1997, el personaje de Carl Jenkins se refiere a su misión, la inteligencia militar, como "juegos y teoría." Uno de los principales mecanismos de juego de toma de decisiones del videojuego de Escape Zero: Última recompensa de la virtud se basa en la teoría de juegos. Algunos de los personajes, incluso la referencia dilema del prisionero. La película Dr. Strangelove satiriza juego las ideas teóricas acerca de la teoría de la disuasión. Por ejemplo, la disuasión nuclear depende de la amenaza de tomar represalias catastróficamente si se detecta un ataque nuclear. Un teórico juego podría argumentar que tales amenazas pueden dejar de ser creíble , en el sentido de que pueden conducir a subjuegos equilibrios imperfectos. La película lleva esta idea un paso más allá, con los rusos irrevocable de comprometerse con una respuesta nuclear catastrófica sin hacer público amenaza. La ciencia y la lógica del ordenador
Filosofía
Ciervo Liebre
Ciervo 3, 3 0, 2 Liebre 2, 0 2, 2 Caza del ciervo Tipos de juegos
Cooperativa o no cooperativo
Simétrica y asimétrica
E F E 1, 2 0, 0 F 0, 0 1, 2 Un juego asimétrico Cero-suma y no de suma cero
La B La -1, 1 3, -3 B 0, 0 -2, 2 Un juego de suma cero Simultánea y secuencial
Secuencial Simultáneo Normalmente denotado por: Árboles de decisión Payoff Matrices El conocimiento previo del movimiento rival: Sí No Tiempo Axis: Sí No También conocido como: Amplia Juego Juego Estratégico Información perfecta y la información imperfecta
Juegos combinatorios
Juegos infinitamente largos
Juegos discretas y continuas
Juegos diferenciales
Muchos jugadores y juegos de población
Resultados estocásticos (y relación con otros campos)
Metajuegos
Historia
Cultura popular
