Historia de las matemáticas
Antecedentes de las escuelas de Wikipedia
SOS Children han producido una selección de artículos de wikipedia para las escuelas desde el año 2005. Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...
| Historia de la ciencia |
|---|
 |
Fondo
|
Por época
|
Por cultura
|
Ciencias Naturales
|
Matemáticas
|
Ciencias Sociales
|
Tecnología
|
Medicina
|
Páginas de navegación
|
El área de estudio conocido como la historia de las matemáticas es principalmente una investigación sobre el origen de los descubrimientos en matemáticas y, en menor medida, una investigación sobre los métodos matemáticos y la notación del pasado.
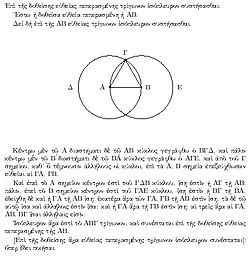
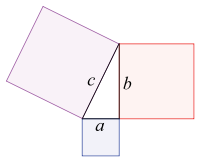
Antes de la era moderna y la difusión mundial del conocimiento, ejemplos escritos de nuevos desarrollos matemáticos han salido a la luz sólo en unos pocos lugares. Los textos más antiguos matemáticos disponibles son Plimpton 322 ( Babilonia matemáticas c. 1900 aC), el Rhind papiro matemático (matemáticas egipcias c. 2000-1800 aC) y la Papiro de Moscú ( Matemáticas egipcias c. 1890 aC). Todos estos textos se refieren a la llamada teorema de Pitágoras , que parece ser el más antiguo y extendido desarrollo matemático después de la aritmética básica y la geometría.
El estudio de las matemáticas como un tema en sí mismo comienza en el siglo sexto antes de Cristo con la Pitagóricos, que acuñó el término "matemáticas" de la antigua μάθημα griego (mathema), que significa "objeto de la instrucción". Matemáticas griegas refinaron grandemente los métodos (especialmente a través de la introducción de razonamiento deductivo y rigor matemático en pruebas ) y amplió el tema de las matemáticas. Matemáticas chinas hicieron contribuciones tempranas, incluyendo un colocar el sistema de valores. La Sistema de numeración hindú-árabe y las reglas para el uso de sus operaciones, en uso en todo el mundo hoy en día, probablemente evolucionaron a lo largo del primer milenio de nuestra era, en la India y se transmitió hacia el oeste a través de las matemáticas islámicas. Matemáticas islámicas, a su vez, desarrollar y ampliar las matemáticas conocidas por estas civilizaciones. Muchos textos griegos y árabes sobre matemáticas eran entonces traducido al latín, lo que llevó a un mayor desarrollo de las matemáticas en la Europa medieval .
Desde la antigüedad a través de las Edad Media , las ráfagas de creatividad matemática fueron seguidas a menudo por siglos de estancamiento. A partir del Renacimiento de Italia en el siglo 16, los nuevos desarrollos matemáticos, interactuando con los nuevos descubrimientos científicos, se hicieron a un ritmo cada vez mayor que continúa hasta nuestros días.
Matemáticas Prehistoria
El origen de matemática mentira pensamiento en los conceptos de número , magnitud, y formulario. Los estudios modernos de la cognición animal han demostrado que estos conceptos no son exclusivas de los seres humanos. Tales conceptos habrían sido parte de la vida cotidiana en las sociedades de cazadores-recolectores. La idea del concepto de "número" que evoluciona gradualmente con el tiempo se apoya en la existencia de lenguas que conservan la distinción entre "uno", "dos", y "muchos", pero no de un mayor número de dos.
El objeto conocido posiblemente matemática más antigua es la Hueso Lebombo, descubierto en las montañas Lebombo de Swazilandia y fechado aproximadamente a 35.000 antes de Cristo. Se compone de 29 muescas distintas cortadas en el peroné de un babuino. También prehistórico artefactos descubiertos en África y Francia , fechados entre 35.000 y 20.000 años de edad, sugieren los primeros intentos de cuantificar el tiempo.
El hueso Ishango , que se encuentra cerca de las cabeceras del Nilo río (noreste de Congo ), puede ser tanto como 20.000 años de edad y se compone de una serie de marcas de conteo talladas en tres columnas que recorren la longitud del hueso. Las interpretaciones comunes son que el hueso Ishango muestra ya sea la manifestación más antigua conocida de secuencias de números primos o un calendario lunar de seis meses. En el libro Cómo Matemáticas sucedió: los primeros 50.000 años, Peter Rudman argumenta que el desarrollo del concepto de los números primos sólo pudo haber ocurrido después de que el concepto de la división, que data de después de 10.000 antes de Cristo, con los números primos probablemente no ser comprendido hasta alrededor del año 500 aC. Él también escribe que "no se ha tratado de explicar por qué un recuento de algo debe exhibir múltiplos de dos números primos, entre 10 y 20, y algunos números que son casi múltiplos de 10." El hueso Ishango, según académico Alexander Marshack, puede haber influido en el desarrollo posterior de las matemáticas en Egipto, al igual que algunas entradas en el hueso Ishango, aritmética egipcia también hizo uso de la multiplicación por 2; esto, sin embargo, está en disputa.
Predinásticos egipcios del quinto milenio antes de Cristo representado pictóricamente geométricos diseños. Se ha afirmado que monumentos megalíticos de Inglaterra y Escocia , que data del 3er milenio antes de Cristo, incorporan ideas geométricas tales como círculos , elipses , y Ternas pitagóricas en su diseño.
Todo lo anterior se disputan sin embargo, y el uso matemático indiscutible actualmente más antigua es en fuentes egipcias y babilónicas dinásticos. Así que tomó los seres humanos por lo menos 45.000 años de la consecución de la modernidad y el lenguaje del comportamiento (generalmente cree que será un largo tiempo antes de eso) para desarrollar la matemática como tal.
La matemática babilónica
Babilonia matemáticas se refiere a nada de matemáticas de la gente de Mesopotamia (actual Irak ) desde los días de los primeros sumerios a través de la Período helenístico casi hasta el amanecer del cristianismo . Se nombra matemáticas babilónicas debido al papel central de Babilonia como un lugar de estudio. Más tarde bajo la Imperio Árabe, Mesopotamia, especialmente Bagdad , una vez más se convirtió en un importante centro de estudio para Matemáticas islámicas.
En contraste con la escasez de fuentes de Matemáticas egipcias, nuestro conocimiento de la matemática babilónica se deriva de más de 400 tablillas de arcilla desenterradas desde la década de 1850. Escrito en Escritura cuneiforme, tabletas fueron inscritos, mientras que la arcilla estaba húmeda, y se cuece duro en un horno o por el calor del sol. Algunas de ellas parecen estar graduada tarea.
La evidencia más temprana de las matemáticas escritas se remonta a los antiguos sumerios , quienes construyeron la primera civilización en Mesopotamia. Ellos desarrollaron un complejo sistema de metrología desde 3000 antes de Cristo. Desde alrededor de 2500 aC en adelante, los sumerios escribieron tablas de multiplicar en tablillas de arcilla y tratado geométricas ejercicios y división problemas. Los primeros rastros de los numerales babilónicos también datan de este período.
La mayoría de las tabletas de arcilla recuperadas datan desde 1800 hasta 1600 antes de Cristo, y cubre temas que incluyen fracciones, álgebra, ecuaciones cuadráticas y cúbicas, y el cálculo de regular recíproca pares. Las tabletas también incluyen tablas y métodos para resolver multiplicación lineal y ecuaciones cuadráticas . La tableta babilónica YBC 7289 da una aproximación de √2 precisa a cinco decimales.
Matemáticas babilónicas fueron escritas usando un sexagesimal (base-60) sistema de numeración . De aquí se deriva el uso moderno día de 60 segundos en un minuto, 60 minutos en una hora, y 360 (60 x 6) grados en un círculo, así como el uso de segundos y minutos de arco para denotar fracciones de un grado. Avances en matemáticas babilónicas fueron facilitadas por el hecho de que 60 tiene muchos divisores. También, a diferencia de los egipcios, griegos y romanos, los babilonios tenían un sistema de valor verdadero, donde los dígitos escritos en la columna de la izquierda representan los valores más grandes, tanto como en el decimal sistema. Carecían, sin embargo, un equivalente del punto decimal, por lo que el valor de posición de un símbolo a menudo tuvo que ser inferido a partir del contexto. Por otro lado, este "defecto" es equivalente a la utilización de hoy en día de la aritmética de punto flotante; Además, el uso de la base de 60 significa que cualquier recíproco de un número entero que es un múltiplo de divisores de 60 tiene necesariamente una expansión finita a la base 60. (En la aritmética decimal, sólo recíprocos de múltiplos de 2 y 5 tienen expansiones decimales finitos. ) Por lo tanto, hay un argumento fuerte de que la aritmética estilo babilónico antiguo es mucho más sofisticado que el de uso actual.
La interpretación de Plimpton 322 era la fuente de controversia durante muchos años después de que se dio cuenta de su importancia en el contexto de triángulos pitagóricos. En el contexto histórico, los problemas de herencia que involucran áreas equivalentes subdivisión de campos triangulares y trapezoidales (con lados de longitud enteros) se convierten rápidamente en la necesidad de calcular la raíz cuadrada de 2, o para resolver la "ecuación de Pitágoras" en números enteros: en lugar de considerar un cuadrado como la suma de dos cuadrados, podemos considerar equivalente de un cuadrado como una diferencia de dos cuadrados. Después de la división, (bis) (c + a) = bb se convierte en el producto de dos números racionales que dan 1: (c / ba / b) (c / b + a / b) = 1. Esto se resuelve fácilmente mediante la consulta de una tabla de pares recíprocos. Las soluciones de la ecuación original son así parametrizada por la elección de un número racional x, a partir del cual derechistas triángulos pitagóricos triples pueden ser fácilmente construidos por entero-escalar un derecho del triángulo con lados de longitud 2x, xx-1, xx + 1 (en caso de un deseo matemático contemporáneo para hacerlo). Todas las ternas pitagóricas surgen de esta manera, y los ejemplos proporcionados en Plimpton 322 implican algunas bastante grandes números, para los estándares modernos, tales como (4601, 4800, 6649) en notación decimal.
Matemáticas egipcias
Egipcia matemáticas se refiere a las matemáticas escritas en el Lengua egipcia. Desde el Período helenístico, griego reemplazó egipcia como el lenguaje escrito de Eruditos egipcios. Estudio matemático en Egipto después continuó bajo la Imperio árabe como parte de Matemáticas islámicas, cuando el árabe se convirtió en el lenguaje escrito de los eruditos egipcios.
El más extenso texto matemático egipcio es el Rhind papiro (a veces también llamado el Papiro de Ahmes de su autor), fechado en c. 1650 aC, pero probablemente una copia de un documento más antiguo de la Reino medio de alrededor de 2000-1800 aC. Se trata de un manual de instrucciones para los estudiantes de la aritmética y la geometría. Además de dar fórmulas y métodos para la multiplicación, la división de la zona y trabajar con fracciones de unidad, sino que también contiene evidencias de otros conocimientos matemáticos, incluyendo compuestos y los números primos , la aritmética , geométrica y medias armónicas; y entendimientos simplistas, tanto de la Criba de Eratóstenes y la teoría de números perfectos (es decir, la del número 6). También muestra cómo resolver primer orden ecuaciones lineales , así como aritmética y serie geométrica.
Otro texto matemático egipcio significativo es el Papiro de Moscú, también de la Período Reino Medio, fechado en c. 1890 antes de Cristo. Consiste en lo que hoy son llamados problemas de palabras o problemas de la historia, que aparentemente estaban destinados como entretenimiento. Un problema se considera que es de particular importancia, ya que da un método para encontrar el volumen de una tronco: "Si le dicen:. Una pirámide truncada de 6 para la altura vertical por 4 en la base por 2 en la parte superior Estás cuadrar este 4, como resultado 16. Usted es duplicar 4, resultado 8. Usted debe cuadrado de 2, como resultado 4. Usted debe agregar el 16, el 8 y el 4, como resultado 28. Usted debe tener un tercio de 6, resultado 2. Usted debe tener 28 dos veces, como resultado 56. Véase, es 56 . Usted encontrará que es correcto ".
Por último, la Berlín papiro (c. 1300 aC) muestra que los antiguos egipcios podían resolver un segundo orden ecuación algebraica.
La matemática griega
La matemática griega se refiere a las matemáticas escritas en el idioma griego desde la época de Tales de Mileto (~ 600 aC) hasta el cierre de la Academia de Atenas en el año 529 AD. Matemáticos griegos vivían en ciudades repartidas por todo el Mediterráneo oriental, desde Italia hasta el norte de África, pero estaban unidos por la cultura y el idioma. Matemáticas griegas de la época siguientes Alejandro Magno a veces se llama matemáticas helenísticas.
La matemática griega era mucho más sofisticado que las matemáticas que habían sido desarrollados por las culturas anteriores. Todos los registros supervivientes de las matemáticas pre-griegas muestran el uso del razonamiento inductivo, es decir, observaciones repetidas utilizan para establecer reglas generales. Matemáticos griegos, por el contrario, utilizan el razonamiento deductivo. Los griegos usaban la lógica para deducir conclusiones a partir de definiciones y axiomas, y utilizado rigor matemático a probar ellos.
La matemática griega se cree que han comenzado con Tales de Mileto (c. 624-c.546 aC) y Pitágoras de Samos (c. 582-c. 507 aC). Aunque el alcance de la influencia se disputa, probablemente estaban inspirados por Egipcia y Matemáticas babilónicas. Según la leyenda, Pitágoras viajó a Egipto para aprender matemáticas, geometría y astronomía de los sacerdotes egipcios.
Thales utilizó la geometría para resolver problemas tales como el cálculo de la altura de las pirámides y la distancia de los barcos de la orilla. Se le atribuye el primer uso del razonamiento deductivo aplicado a la geometría, derivando cuatro corolarios a Teorema de Thales. Como resultado, ha sido aclamado como el primer matemático verdadero y el individuo primero conocido a quien un descubrimiento matemático se ha atribuido. Pitágoras estableció el Pitágoras Escuela, cuya doctrina era que las matemáticas gobernaron el universo y cuyo lema era "todo es número". Fueron los pitagóricos que acuñó el término "matemáticas", y con la que comienza el estudio de las matemáticas por su propio bien. Los pitagóricos se le atribuye la primera prueba del teorema de Pitágoras , aunque la declaración del teorema tiene una larga historia, y con la prueba de la existencia de los números irracionales .
Platón (428/427 aC - 348/347 aC) es importante en la historia de las matemáticas para inspirar y guiar a otros. Su Academia Platónica, en Atenas , se convirtió en el centro de la matemática del mundo en el siglo cuarto, y fue de esta escuela que los principales matemáticos de la época, tales como Eudoxo de Cnido, vino. Platón también discutió los fundamentos de las matemáticas, aclaró algunas de las definiciones (por ejemplo, la de una línea como "longitud sin anchura"), y reorganizó los supuestos. El método analítico se atribuye a Platón, mientras que una fórmula para la obtención de ternas pitagóricas lleva su nombre.
Eudoxo (408-c.355 aC) desarrolló el método de agotamiento, un precursor de la moderna integración y una teoría de las relaciones que evitaron el problema de magnitudes inconmensurables . El primero permitió a los cálculos de áreas y volúmenes de figuras curvilíneas, mientras que el segundo habilitado geómetras posteriores para hacer avances significativos en la geometría. A pesar de que no hizo descubrimientos matemáticos técnicos específicos, Aristóteles (384-c.322 aC) contribuyó significativamente al desarrollo de las matemáticas por sentar las bases de la lógica .
En el siglo tercero antes de Cristo, el primer centro de enseñanza de las matemáticas y la investigación fue la Musaeum de Alejandría . Fue allí donde Euclides (c. 300 aC) enseñó, y escribió el elementos , ampliamente considerado como el libro de texto más exitoso e influyente de todos los tiempos. Los elementos introducidos rigor matemático a través de la método axiomático y es el primer ejemplo de formato todavía se utiliza en las matemáticas de hoy, la de definición, axioma, teorema, y la prueba. Aunque la mayor parte de los contenidos de los elementos que ya se conocían, Euclides los colocó en un único marco lógico y coherente. Los elementos se sabe que todas las personas educadas en Occidente hasta mediados del siglo 20 y su contenido todavía se enseñan en las clases de geometría en la actualidad. Además de los teoremas familiares de la geometría euclidiana , los elementos se entiende como un libro de texto de introducción a todos los temas matemáticos de la época, como la teoría de números , álgebra y geometría sólida, incluyendo pruebas de que la raíz cuadrada de dos es irracional y que hay infinitos números primos. Euclides también escribió extensamente sobre otros temas, como las secciones cónicas , la óptica , geometría esférica, y la mecánica, pero sólo la mitad de sus escritos sobrevivir.
La primera mujer matemática registrado por la historia era Hipatia de Alejandría (AD 350-415). Ella sucedió a su padre como bibliotecario en la Gran Biblioteca y escribió numerosas obras sobre matemáticas aplicadas. Debido a que era una mujer, la comunidad cristiana en Alejandría la castigó por su presunción desnudándola y el raspado de la piel con conchas de almeja (algunos dicen tejas).
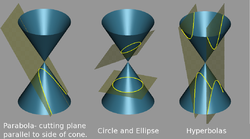
Arquímedes (BC c.287-212) de Syracuse, ampliamente considerado como el más grande matemático de la antigüedad, que se utiliza el método de agotamiento para calcular el área bajo el arco de parábola con la la suma de una serie infinita, de una manera no muy diferente de cálculo moderno. También mostró que uno podría utilizar el método de agotamiento para calcular el valor de π con tanta precisión como se desee, y obtuvo el valor más exacto de π entonces conocido, 3 10/71 <π <3 10/70. También estudió la espiral que lleva su nombre, obtuvo fórmulas para los volúmenes de superficies de revolución (paraboloide, elipsoide, hiperboloide), y un ingenioso sistema para expresar números muy grandes. Mientras que él también es conocido por sus contribuciones a la física y varios dispositivos mecánicos avanzados, el mismo Arquímedes puso mucho más valor en los productos de su pensamiento y principios matemáticos generales. Él consideraba su mayor logro de su hallazgo de la superficie y el volumen de una esfera, que obtuvo al probar estos son 2/3 de la superficie y el volumen de un cilindro que circunscribe la esfera.
Apolonio de Perge (c. 262-190 BC) hizo avances significativos para el estudio de las secciones cónicas , que muestra que uno puede obtener los tres variedades de sección cónica variando el ángulo del plano que corta un cono doble napped. Él también acuñó la terminología en uso hoy en día para las secciones cónicas, a saber, parábola ("colocar al lado" o "comparación"), "elipse" ("deficiencia"), y "hipérbola" ("más allá de un tiro"). Su trabajo de cónicas es uno de los trabajos matemáticos más conocidos y conservados de la antigüedad, y en él se deriva muchos teoremas relativos a las secciones cónicas que probarían un valor incalculable para los matemáticos y astrónomos posteriores que estudian el movimiento planetario, como Isaac Newton. Aunque ni Apolonio ni ningún otro matemáticos griegos dieron el salto a la geometría analítica, el tratamiento de Apolonio de curvas es en cierto modo similar al tratamiento moderno, y algunas de sus obras parece anticipar el desarrollo de la geometría analítica de Descartes unos 1800 años después.
Por la misma época, Eratóstenes de Cirene de Cirene (c. 276-194 aC) ideó el Criba de Eratóstenes para encontrar números primos . El siglo tercero antes de Cristo es generalmente considerada como la "Edad de Oro" de la matemática griega, con los avances en las matemáticas puras a partir de ahora en relativa decadencia. Sin embargo, en los siglos que siguieron se hicieron avances significativos en matemáticas aplicadas, especialmente la trigonometría , en gran parte para hacer frente a las necesidades de los astrónomos. Hiparco de Nicea (c. 190-120 aC) es considerado el fundador de la trigonometría para compilar la tabla trigonométrica primero conocido, ya él se debe también la utilización sistemática del círculo de 360 grados. Herón de Alejandría (c. 10-70 dC) se le atribuye La fórmula de Herón para calcular el área de un triángulo escaleno y con ser los primeros en reconocer la posibilidad de que los números negativos que poseen raíces cuadradas. Menelao de Alejandría (c. 100 dC), precursor trigonometría esférica a través Teorema de Menelao. El trabajo trigonométrica más completa e influyente de la antigüedad es el Almagesto de Ptolomeo (c. 90-168 dC), un tratado astronómico hito cuyas tablas trigonométricas sería utilizado por los astrónomos durante los próximos mil años. Tolomeo también se acredita con El teorema de Ptolomeo para derivar cantidades trigonométricas, y el valor más exacto de π fuera de China, hasta la época medieval, 3.1416.
Tras un período de estancamiento después de Ptolomeo, el período comprendido entre 250 y 350 dC se conoce como la "Edad de Plata" de las matemáticas griegas veces. Durante este período, Diofanto hizo avances significativos en álgebra , en particular análisis indeterminado, que también se conoce como "análisis de Diophantine". El estudio de Ecuaciones diofánticas y Aproximaciones diofánticas es un área importante de la investigación en la actualidad. Su obra principal fue la Aritmética, una colección de 150 problemas algebraicos tratar con soluciones exactas para determinar y ecuaciones indeterminadas. La Arithmetica tuvo una influencia significativa en los matemáticos posteriores, como Pierre de Fermat , que llegó a su famoso teorema pasado después de tratar de generalizar un problema que había leído en la Aritmética (la de dividir un cuadrado en dos plazas). Diofanto también hizo avances significativos en la notación, la Arithmetica ser el primer ejemplo de simbolismo algebraico y la síncopa.
Matemáticas chino
La matemática china temprana es tan diferente de la de otras partes del mundo que es razonable suponer un desarrollo independiente. El texto matemático más antiguo existente de China es el Chou Pei Suan Ching, de fecha diversamente entre 1200 aC y 100 aC, aunque la fecha de 300 aC parece razonable.
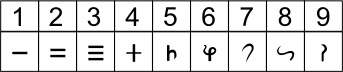
De particular interés es el uso de las matemáticas chinas de un sistema de notación posicional decimal, los llamados "números de la vara" en los que se utilizaron cifras distintas de los números entre 1 y 10, y sistemas de cifrado adicionales para potencias de diez. Así, el número 123 se escribiría con el símbolo de "1", seguido por el símbolo de "100", el símbolo de "2", seguido por el símbolo de "10", seguido por el símbolo de "3". Este fue el sistema de numeración más avanzado del mundo en ese momento, al parecer en el uso de varios siglos antes de la era común, y mucho antes de que el desarrollo del sistema de numeración indio. Números de la vara permite la representación de los números tan grandes como los cálculos deseados y se deja que se realizarán en el pan suan, o ábaco chino. La fecha de la invención de la sartén suan no es cierto, pero el primer escrito mención data desde el año 190, en las Notas Complementarias de Xu Yue en el arte de las figuras.
La obra más antigua existente en la geometría en China proviene de la filosofía Mohist canon c. 330 aC, compilado por los seguidores de Mozi (470-390 aC). El Mo Jing describe varios aspectos de muchos campos relacionados con la ciencia física, y proporcionó un pequeño número de teoremas geométricos también.
En 212 aC, el emperador Qin Shi Huang (Shi Huang-ti) ordenó a todos los libros en el Imperio Qin distintos oficialmente sancionados los quemarán. Este decreto no fue universalmente obedeció, pero como consecuencia de esta pequeña orden se conoce acerca de las antiguas matemáticas chinas antes de esta fecha. Después de la quema de libros de 212 aC, el Dinastía Han (202 aC-220 dC), produjo obras de la matemática que, presumiblemente, se expandieron en las obras que se iban a perder. El más importante de ellos es Los nueve capítulos en el arte matemático, el título completo de la que aparecieron por AD 179, pero existían en parte con otros títulos de antemano. Se compone de 246 problemas que involucren la agricultura, los negocios, el empleo de la geometría para calcular palmos de altura y proporciones de dimensión para Torres pagoda china, la ingeniería, topografía, e incluye material sobre triángulos rectángulos y los valores de π . Creó prueba matemática para el teorema de Pitágoras , y una fórmula matemática para la eliminación de Gauss . Liu Hui comentó sobre el trabajo en el siglo tercero dC, y dio un valor de π precisa a 5 decimales. Aunque más de una cuestión de resistencia de cálculo que la comprensión teórica, en el siglo 5 dC Zu Chongzhi calcula el valor de π a siete cifras decimales, que seguía siendo el valor más exacto de π durante casi los próximos 1000 años. También estableció un método que más tarde se llamaría Principio de Cavalieri para encontrar el volumen de una esfera .
La cota máxima de las matemáticas chinas se produce en el siglo 13 (última parte del período Sung ), con el desarrollo del álgebra china. El texto más importante de este periodo es el Espejo precioso de los cuatro elementos por Chu Shih-chieh (fl. 1280-1303), que trata de la solución de ecuaciones algebraicas de orden superior simultáneas utilizando un método similar al El método de Horner. El Espejo precioso también contiene un diagrama del triángulo de Pascal con coeficientes de expansión binomial a través de la octava potencia, aunque ambos aparecen en obras chinas ya en 1100. El chino también hizo uso del complejo diagrama combinatoria conocido como el cuadrado mágico y círculos mágicos, que se describen en la antigüedad y perfeccionadas por Yang Hui (1238-1298 dC).
Incluso después de las matemáticas europeas comenzaron a florecer durante el Renacimiento , las matemáticas europeas y chinas fueron las tradiciones distintas, con salida matemático chino significativa en declive desde el siglo 13 en adelante. Misioneros jesuitas como Matteo Ricci llevó las ideas matemáticas de ida y vuelta entre las dos culturas desde el 16 al 18 siglos, aunque en este punto las ideas mucho más matemáticos estaban entrando en China que salir.
La matemática india
La primera civilización en el subcontinente indio es la civilización del valle del Indo , que floreció entre 2600 y 1900 antes de Cristo en el río Indus cuenca. Sus ciudades fueron diseñadas con regularidad geométrica, pero no hay documentos matemáticos conocidos sobreviven de esta civilización.
Los registros más antiguos existentes matemáticos de la India son el Sulba Sutras (fecha diversamente entre el siglo I aC y el siglo octavo segundo dC), apéndices de textos religiosos que dan reglas simples para la construcción de altares de varias formas, como cuadrados, rectángulos, paralelogramos y otros. Al igual que en Egipto, la preocupación por las funciones del templo apunta a un origen de las matemáticas en el ritual religioso. Los Sutras Sulba dan métodos para construir un círculo con aproximadamente la misma área que un cuadrado dado, lo que implica varias aproximaciones diferentes del valor de π . Además, se calculan la raíz cuadrada de 2 a varias cifras decimales, lista ternas pitagóricas, y dan una declaración del teorema de Pitágoras . Todos estos resultados están presentes en las matemáticas babilónicas, lo que indica la influencia mesopotámica. No se sabe hasta qué punto los Sutras Sulba influenciados matemáticos más tarde indias. Al igual que en China, hay una falta de continuidad en las matemáticas indias; avances significativos están separados por largos períodos de inactividad.
Pāṇini (c. Siglo quinto antes de Cristo) formuló las reglas para Gramática sánscrita. Su notación es similar a la notación matemática moderna, y se utiliza metareglas, transformaciones, y recursividad. Pingala (aproximadamente tercero-primero siglos antes de Cristo) en su tratado de prosodia utiliza un dispositivo correspondiente a un sistema de numeración binaria . Su discusión de los combinatoria de metros corresponde a una versión elemental de la teorema del binomio. La obra de Pingala también contiene las ideas básicas de los números de Fibonacci (llamado mātrāmeru).
Los siguientes documentos matemáticos importantes de la India después de los Sutras Sulba son los Siddhantas, tratados astronómicos desde la quinta siglos cuarto y AD ( Periodo Gupta) que muestra una fuerte influencia helenística. Ellos son importantes porque contienen la primera instancia de las relaciones trigonométricas basados en la media-acorde, como es el caso en la trigonometría moderna, en lugar de la cuerda completa, como fue el caso en Ptolemaic trigonometría. A través de una serie de errores de traducción, las palabras "seno" y "coseno" derivan de la "jiya" sánscrito y "Kojiya".
En el siglo 5 dC, Aryabhata escribió el Aryabhatiya, un delgado volumen, escrito en verso, destinadas a completar las reglas de cálculo utilizados en la astronomía y la medición matemática, aunque sin ningún sentimiento de lógica o metodología deductiva. Aunque cerca de la mitad de las entradas que están mal, es en el Aryabhatiya que el sistema de valor decimal aparece por primera vez. Varios siglos después, la Matemático musulmán Abu Rayhan Biruni describe la Aryabhatiya como una "mezcla de piedras y cristales comunes costosos".
En el siglo séptimo, Brahmagupta identificó la Teorema de Brahmagupta, Identidad de Brahmagupta y La fórmula de Brahmagupta, y por primera vez, en Brahma-Sphuta-siddhanta, explicó lúcidamente el uso de cero tanto como un marcador de posición y dígito decimal , y explicó el Sistema de numeración hindú-árabe. Fue a partir de una traducción de este texto indio en matemáticas (c. 770) que los matemáticos islámicos fueron introducidas a este sistema de numeración, que se adaptaron como números arábigos . Eruditos islámicos llevaron a conocimiento de este sistema numérico a Europa en el siglo 12, y ahora se ha desplazado a todos los sistemas de números mayores de todo el mundo. En el siglo 10, El comentario de Halayudha en La obra de Pingala contiene un estudio de la secuencia de Fibonacci y el triángulo de Pascal , y describe la formación de una matriz .
En el siglo 12, Bhaskara II vivió en el sur de la India y escribió extensamente sobre todas las ramas de las matemáticas conocidas entonces. Su obra contiene objetos matemáticos equivalentes o aproximadamente equivalente a infinitesimales, derivados, el teorema de valor medio y la derivada de la función seno. ¿En qué medida se anticipó a la invención del cálculo es un tema controvertido entre los historiadores de las matemáticas.
En el siglo 14, Madhava de Sangamagrama, el fundador de la llamada Escuela de Kerala de Matemáticas, encontró el Serie Madhava-Leibniz, y, usando 21 términos, calcula el valor de π como 3,14159265359. Madhava también encontró la serie de Madhava-Gregory para determinar el arcotangente, la-Newton Madhava serie de potencias para determinar seno y el coseno y la aproximación de Taylor para funciones seno y coseno. En el siglo 16, Jyesthadeva consolida muchos de los desarrollos y los teoremas de la Escuela de Kerala en la Yukti-Bhasa. Sin embargo, la Escuela de Kerala no formuló una teoría sistemática de la diferenciación y la integración , ni tampoco existe ninguna prueba directa de sus resultados que se transmite fuera de Kerala. Los avances en las matemáticas, junto con otros campos de la ciencia se estancó en la India con el establecimiento de El dominio musulmán en la India.
Matemáticas islámica
La Imperio Islámico establecido a través de Persia , el Oriente Medio , Asia Central, África del Norte , Iberia, y en algunas partes de la India en el siglo octavo hicieron contribuciones significativas hacia las matemáticas. Aunque la mayoría de los textos islámicos en matemáticas fueron escritos en árabe , la mayoría de ellos no fueron escritos por los árabes , ya que al igual que el estado de griego en el mundo helenístico, árabe fue utilizado como el lenguaje escrito de los eruditos no árabes en todo el mundo islámico en el tiempo. Persas contribuyeron al mundo de Matemáticas junto a los árabes.
En el siglo noveno, la Matemático persa Muhammad ibn Musa al-Khwarizmi escribió varios libros importantes sobre los números indo-arábigos y sobre los métodos para resolver ecuaciones. Su libro sobre el cálculo con números hindúes , escrito alrededor 825, junto con el trabajo de Al-Kindi, jugaron un papel decisivo en la difusión de las matemáticas indias y numeración india a Occidente. La palabra algoritmo se deriva de la latinización de su nombre, Algoritmi, y la palabra álgebra del título de una de sus obras, Al-Kitab al-Mujtasar fî Hisab al-Gabr wa'l-muqabala ( El Libro compendioso de Cálculo por Terminación y equilibrio ). Él dio una explicación exhaustiva de la solución algebraica de ecuaciones de segundo grado con raíces positivas, y él fue el primero en enseñar álgebra en una forma elemental y por su propio bien. También discutió el método fundamental de la " reducción "y" equilibrio ", en referencia a la transposición de términos restados al otro lado de una ecuación, es decir, la cancelación de términos como en lados opuestos de la ecuación. Esta es la operación que al-Khwarizmi describió originalmente como al-Jabr . Su álgebra también fue mayor en cuestión no "con una serie de problemas que hay que resolver, sino una exposición que comienza con términos primitivos en los que las combinaciones deben dar todos los prototipos posibles de ecuaciones, que de ahora en adelante constituyen explícitamente el verdadero objeto de estudio. " También estudió una ecuación para su propio bien y "de manera genérica, en la medida que no se limita a surgir en el curso de la solución de un problema, pero se llama específicamente a definir una clase infinita de problemas."
Otros desarrollos en álgebra fueron hechas por Al-Karaji en su tratado al-Fakhri , donde se extiende la metodología para incorporar potencias enteras y raíces enteras de cantidades desconocidas. Algo parecido a una prueba por inducción matemática aparece en un libro escrito por Al-Karaji alrededor del año 1000, que lo utilizó para demostrar el teorema del binomio, el triángulo de Pascal , y la suma de integrales cubos. La historiador de las matemáticas, F. Woepcke, elogió Al -Karaji por ser "el primero que introdujo la teoría de algebraica cálculo . " También en el siglo 10, Abul Wafa tradujo las obras de Diofanto al árabe. Ibn al-Haytham fue el primer matemático para deducir la fórmula para la suma de las potencias cuartas, utilizando un método que es fácilmente generalizable para determinar la fórmula general para la suma de las potencias enteras. Él realizó una integración con el fin de encontrar el volumen de un paraboloide, y fue capaz de generalizar su resultado para las integrales de polinomios hasta el cuarto grado. Él por lo tanto estuvo cerca de encontrar una fórmula general para las integrales de polinomios, pero no se ocupa de ningún polinomios más altos que el cuarto grado.
A finales del siglo 11, Omar Khayyam escribió Las discusiones sobre las dificultades en Euclid , un libro sobre lo que él percibe como fallas en de Euclides elementos , especialmente el postulado de las paralelas. También fue el primero en encontrar la solución geométrica en general a las ecuaciones cúbicas. También fue muy influyente en la reforma del calendario.
En el siglo 13, Nasir al-Din Tusi (Nasireddin) hizo avances en la trigonometría esférica. También escribió influyente obra de Euclides 's postulado de las paralelas. En el siglo 15, Ghiyath al-Kashi calcula el valor de π a la posición decimal 16a. Kashi también tenía un algoritmo para calcular n º raíces, que era un caso especial de los métodos dados muchos siglos después por Ruffini y Horner.
Otros logros de los matemáticos musulmanes durante este período incluyen la adición de lanotación decimal de losnúmeros arábigos, el descubrimiento de todas las modernasfunciones trigonométricasademás del seno,la introducción de al-Kindi decriptoanálisis yanálisis de frecuencia, el desarrollo dela geometría analíticaporIbn al-Haytham, el comienzo dela geometría algebraica porOmar Khayyam y el desarrollo de unanotación algebraica poral-Qalasadi.
Durante la época delImperio Otomanoy elImperio Safávida en el siglo 15, el desarrollo de las matemáticas islámicas se estancó.
Matemáticas Europea Medieval
Interés europeo medieval en matemáticas fue impulsado por preocupaciones muy diferentes de las de los matemáticos modernos. Un elemento de conducción fue la creencia de que las matemáticas siempre la clave para entender el orden creado de la naturaleza, con frecuencia justifica por Platón 's Timeo y el pasaje bíblico (en el libro de la Sabiduría ) que Dios había ordenado a todas las cosas en la medida, y el número y de peso .
Boecio proporcionó un lugar para las matemáticas en el currículo en el siglo sexto cuando acuñó el término quadrivium para describir el estudio de la aritmética, geometría, astronomía y música. Él escribió De arithmetica institutione , una traducción libre del griego de Nicómaco de Introducción a la Aritmética ; De institutione musica , también derivado de fuentes griegas; y una serie de extractos de Euclides 's elementos . Sus obras fueron teórica, en lugar de práctica, y fueron la base de estudio matemático hasta que la recuperación de las obras matemáticas griegas y árabes.
En el siglo 12, los eruditos europeos viajaron a España y Siciliaen busca de textos científicos árabes, incluyendoal-Khwarizmi's El Libro compendioso en Cálculo de Terminación y de equilibrio, traducido al latín porRoberto de Chester, y el texto completo de lade EuclidesElementos, traducidos en varias versiones porAdelardo de Bath,Herman de Carintia, yGerardo de Cremona.
Estas nuevas fuentes provocó una renovación de las matemáticas. Fibonacci, escribiendo en el Liber Abaci , en 1202 y actualizado en 1254, produjeron las primeras matemáticas significativas en Europa desde la época de Eratóstenes, un espacio de más de mil años. El trabajo presenta los números indo-arábigos a Europa, y discutió otros muchos problemas matemáticos.
El siglo 14 vio el desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. Una contribución importante fue el desarrollo de las matemáticas del movimiento local.
Thomas Bradwardine propone que la velocidad (V) aumenta en proporción aritmética como la relación de la fuerza (F) a la resistencia (R) aumenta en proporción geométrica. Bradwardine expresó este por una serie de ejemplos concretos, pero aunque el logaritmo aún no había sido concebido, podemos expresar su conclusión anacrónicamente escribiendo: V = log (F / R). El análisis de Bradwardine es un ejemplo de la transferencia de una técnica matemática utilizada por al-Kindi y Arnald de Villanova para cuantificar la naturaleza de medicamentos compuesto a un problema físico diferente.
Uno de los del siglo 14Oxford Calculadoras,William Heytesbury, carente decálculo diferencial y el concepto delímites, propuestos para medir la velocidad instantánea "por el camino quepodríaser descrito por [un cuerpo]si... que fueron trasladados de manera uniforme al mismo grado de rapidez con que se mueve en ese instante dado ".
Heytesbury y otros determinaron matemáticamente la distancia recorrida por un cuerpo sometido a movimiento uniformemente acelerado (hoy resuelto porla integración), afirmando que "un cuerpo en movimiento uniformemente adquirir o perder ese incremento [de velocidad] atravesará en algún momento dado una [distancia] completamente iguales a la que sería atravesar si se mueve continuamente a través del mismo tiempo con el grado medio [de velocidad] ".
Nicole Oresme en la Universidad de París y el italiano Giovanni di Casali siempre independientemente manifestaciones gráficas de esta relación, afirmando que el área bajo la línea que representa la aceleración constante, representa la distancia total recorrida. En un comentario matemática más tarde de Euclides Elementos , Oresme hizo un análisis general más detallado en el que demostró que un cuerpo adquirirá en cada incremento sucesivo de tiempo un incremento de cualquier cualidad que aumenta a medida que los números impares. Desde Euclides había demostrado la suma de los números impares son los números cuadrados, la calidad total adquirido por el cuerpo aumenta con el cuadrado del tiempo.
Matemáticas Renacimiento
Durante el Renacimiento , el desarrollo de las matemáticas y de la contabilidad se entrelazan. Si bien no existe una relación directa entre el álgebra y la contabilidad, la enseñanza de las materias y los libros publicados a menudo destinada a los hijos de los comerciantes que fueron enviados a escuelas de cómputo (en Flandes y Alemania ) o el ábaco escuelas (conocido como ábaco en Italia), donde aprendieron las habilidades útiles para el comercio y el comercio. Probablemente no hay necesidad de álgebra en la realización de operaciones de contabilidad, pero para las operaciones de trueque complejos o el cálculo del interés compuesto, un conocimiento básico de la aritmética era obligatorio y el conocimiento del álgebra fue muy útil.
Luca Pacioli de "Summa de Aritmética, Geometría, Proportioni et Proportionalità" (en italiano: "Examen de Aritmética , Geometría , Razón y Proporción ") fue impreso y publicado en primera Venecia en 1494. Incluía una de 27 páginas Tratado sobre teneduría de libros, "Particularis de Computis et Scripturis " (italiano: "Detalles de Cálculo y Registro"). Fue escrito principalmente para, y se vende principalmente a los comerciantes que utilizan el libro como un texto de referencia, como una fuente de placer de los problemas matemáticos que contenía, y para ayudar a la educación de sus hijos. En Summa Arithmetica , Pacioli introdujo símbolos de más y menos, por primera vez en un libro impreso, que se convirtieron en símbolos de notación estándar en matemáticas renacentistas italianos. Summa Arithmetica fue también el primer libro conocido impreso en Italia para contener el álgebra . Es importante tener en cuenta que el propio Pacioli había prestado gran parte de la obra de Piero Della Francesca quien plagió.
En Italia, durante la primera mitad del siglo 16, Scipione del Ferro y Niccolò Fontana Tartaglia descubrieron soluciones para ecuaciones cúbicas. Gerolamo Cardano los publicó en su libro de 1545 Ars Magna , junto con una solución de las ecuaciones de cuarto grado, descubierto por su alumno Lodovico Ferrari. En 1572 Rafael Bombelli publicó su L'Algebra en el que mostró cómo hacer frente a las cantidades imaginarias que pudieran aparecer en la fórmula de Cardano para resolver ecuaciones cúbicas.
El libro de Simon StevinDe Thiende('el arte de décimas'), publicado por primera vez en Holanda en 1585, contenía el primer tratamiento sistemático dela notación decimal, que influyó en todo el trabajo posterior en elsistema de números reales.
Impulsada por las demandas de la navegación y la creciente necesidad de mapas precisos de grandes áreas,la trigonometríacreció hasta convertirse en una rama importante de las matemáticas.Bartholomaeus Pitiscus fue el primero en usar la palabra, publicando suTrigonometriaen 1595. tabla de senos y cosenos de Regiomontano fue publicado en 1533.
Durante el Renacimiento el deseo de los artistas para representar el mundo natural de manera realista, junto con la filosofía redescubierta de los griegos, dirigido a los artistas a estudiar matemáticas. También fueron los ingenieros y arquitectos de la época, y así tenían necesidad de las matemáticas, en cualquier caso. El arte de la pintura en perspectiva, y la evolución de la geometría que participan, se estudiaron intensamente.
Matemáticas durante la Revolución Científica
Siglo 17
El siglo 17 vio una explosión sin precedentes de ideas matemáticas y científicas de toda Europa. Galileo observó las lunas de Júpiter en órbita alrededor de ese planeta, usando un telescopio basado en un juguete importado de Holanda. Tycho Brahe había reunido una enorme cantidad de datos matemáticos que describen el posiciones de los planetas en el cielo. A través de su posición como ayudante de Brahe, Johannes Kepler fue expuesto primero y seriamente interactuó con el tema del movimiento planetario. Cálculos de Kepler se hicieron más simple por la invención contemporánea de logaritmos por John Napier y Jost Bürgi. Kepler tuvo éxito en la formulación de leyes matemáticas del movimiento planetario. La geometría analítica desarrollada por René Descartes (1596-1650) permitió a esas órbitas que se trazan en un gráfico, en coordenadas cartesianas . Simon Stevin (1585) creó la base para la moderna notación decimal capaz de describir todos los números, ya sea racional o irracional.
Basándose en trabajos anteriores de muchos predecesores, Isaac Newton descubrió las leyes de la física que explica las leyes de Kepler , y reunió a los conceptos ya conocidos como cálculo infinitesimal. Independientemente, Gottfried Wilhelm Leibniz desarrolló el cálculo y gran parte de la notación del cálculo todavía en uso hoy en día. Ciencia y matemáticas se habían convertido en una empresa internacional, que pronto se extendió por el mundo entero.
Además de la aplicación de las matemáticas a los estudios de los cielos, las matemáticas aplicadas comenzaron a expandirse hacia nuevas áreas, con la correspondencia de Pierre de Fermat y Blaise Pascal . Pascal y Fermat establecen las bases para las investigaciones de la teoría de probabilidades y las normas correspondientes de la combinatoria en sus discusiones sobre un juego de los juegos de azar. Pascal, con su apuesta, intentado utilizar la teoría de la probabilidad de reciente desarrollo para argumentar a favor de una vida dedicada a la religión, en la base de que, incluso si la probabilidad de éxito era pequeña, las recompensas eran infinitas. En cierto sentido, esto prefiguró el desarrollo de la teoría de la utilidad en el siglo 18o a 19no.
Siglo 18
El matemático más influyente del siglo 18 fue sin duda Leonhard Euler . Sus contribuciones van desde la fundación del estudio de la teoría de grafos con los siete puentes de Königsberg problema a la normalización de muchos términos y notaciones matemáticas modernas. Por ejemplo, nombró a la raíz cuadrada de menos 1 con el símbolo i , y se popularizó el uso de la letra griega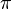 
para representar la relación de la circunferencia de un círculo y su diámetro. Hizo numerosas contribuciones al estudio de la topología, teoría de grafos, cálculo, la combinatoria y análisis complejo, como lo demuestra la multitud de teoremas y notaciones nombrados por él.
Otros matemáticos europeos importantes del siglo 18 incluyenJoseph Louis Lagrange, que hizo un trabajo pionero en la teoría de números, álgebra, cálculo diferencial y el cálculo de variaciones, yLaplace, que, en la época deNapoleón, hicieron un trabajo importante sobre los cimientos deceleste la mecánica y enlas estadísticas.
La matemática moderna
Siglo 19
A lo largo del siglo 19 las matemáticas se convirtieron cada vez más abstracto. En el siglo 19 vivió Carl Friedrich Gauss (1777-1855). Dejando a un lado sus muchas contribuciones a la ciencia, en la matemática pura que hizo un trabajo revolucionario en funciones de variables complejas, en la geometría y en la convergencia de serie. Él dio las primeras pruebas satisfactorias del teorema fundamental del álgebra y de la ley de reciprocidad cuadrática.
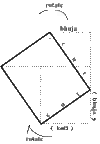
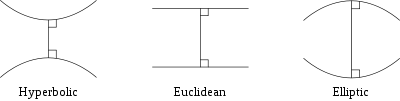
Este siglo vio el desarrollo de las dos formas de la geometría no euclidiana, donde el postulado de las paralelas de la geometría euclidiana ya no se sostiene. El matemático ruso Nikolai Ivanovich Lobachevsky y su rival, el matemático húngaro János Bolyai, definido de forma independiente y estudiaron geometría hiperbólica, donde la singularidad de paralelos ya no se sostiene. En esta geometría la suma de los ángulos de un triángulo suman menos de 180 °. geometría elíptica se desarrolló más tarde en el siglo 19 por el matemático alemán Bernhard Riemann ; aquí hay paralelo se puede encontrar y los ángulos de un triángulo suman a más de 180 °. Riemann desarrolló también la geometría de Riemann, que unifica y generaliza ampliamente los tres tipos de geometría, y se define el concepto de un colector , que generaliza las ideas de curvas y superficies.
El siglo 19 vio el comienzo de una gran cantidad de álgebra abstracta . Hermann Grassmann en Alemania dio una primera versión de los espacios vectoriales , William Rowan Hamilton en Irlanda desarrolló el álgebra no conmutativa. El matemático británico George Boole ideó un álgebra que pronto se convirtió en lo que ahora se llama el álgebra de Boole, en la que los únicos números fueron 0 y 1. álgebra de Boole es el punto de partida de la lógica matemática y tiene importantes aplicaciones en ciencias de la computación .
Augustin-Louis Cauchy,Bernhard Riemann, yKarl Weierstrass reformularon el cálculo de una manera más rigurosa.
También, por primera vez, se exploraron los límites de las matemáticas. Niels Henrik Abel, un noruego, y Evariste Galois, un francés, demostraron que no existe un método algebraico general para resolver ecuaciones polinómicas de grado mayor que cuatro ( Abel-Ruffini teorema ). Otros matemáticos del siglo 19 utilizaron esto en sus pruebas de que regla y compás solos no son suficientes para trisecar un ángulo arbitrario, para construir el lado de un cubo de dos veces el volumen de un cubo dado, ni para construir una plaza igual en la zona a un determinado círculo. Los matemáticos habían intentado en vano de resolver todos estos problemas desde la época de los antiguos griegos. Por otra parte, la limitación de tres dimensiones en la geometría fue superado en el siglo 19 a través de consideraciones de espacio de parámetros y números hipercomplejos.
Investigaciones Abel y Galois de en las soluciones de diferentes ecuaciones polinómicas sentaron las bases para la posterior evolución de la teoría de grupos , y los campos asociados de álgebra abstracta . En el vigésimo siglo los físicos y otros científicos han visto la teoría de grupos como el camino ideal para estudiar la simetría .
En la tarde del siglo 19, Georg Cantor estableció las primeras bases de la teoría de conjuntos , lo que permitió el tratamiento riguroso de la noción del infinito y se ha convertido en el lenguaje común de casi todas las matemáticas. La teoría de conjuntos de Cantor, y el surgimiento de la lógica matemática en manos de Peano, LEJ Brouwer, David Hilbert , Bertrand Russell y AN Whitehead, iniciaron un debate de larga data sobre la fundamentos de las matemáticas.
El siglo 19 vio la fundación de una serie de sociedades matemáticas nacionales: laSociedad Matemática de Londres en 1865, laSociété Mathématique de Francia en 1872, elCircolo Matematico di Palermo en 1884, laSociedad Matemática de Edimburgo en 1883, y de laSociedad Americana de Matemáticas en 1888. La primera, la sociedad internacional de intereses especiales, laSociedad Quaternion, se formó en 1899, en el contexto de unacontroversia vectorial.
En 1897, introdujo Henselnúmeros p-adic.
Siglo 20
El siglo 20 vio las matemáticas se convierten en una profesión importante. Cada año, miles de nuevos doctores en matemáticas se otorgan, y el empleo están disponibles tanto en la enseñanza y la industria.
En un discurso de 1900 en el Congreso Internacional de Matemáticos, David Hilbert propuso una lista de 23 problemas sin resolver en las matemáticas. Estos problemas, que abarca muchas áreas de las matemáticas, formaron un foco central de gran parte de las matemáticas del siglo 20. Hoy en día, 10 se han resuelto, 7 están parcialmente resueltos, y 2 son todavía abierto. El restante 4 se formulan demasiado flojo para ser declarado como resuelto o no.
Conjeturas históricas notables fueron finalmente probados. En 1976, Wolfgang Haken y Kenneth Appel utiliza una computadora para demostrar el teorema de los cuatro colores . Andrew Wiles, basándose en el trabajo de los demás, demostró Último Teorema de Fermat en 1995. Paul Cohen y Kurt Gödel demostró que la hipótesis del continuo es independiente de (posible ni ser probado ni refutado de) los axiomas estándar de la teoría de conjuntos. En 1998 Thomas Callister Hales demostró la conjetura de Kepler.
Colaboraciones matemáticos de tamaño y alcance sin precedentes tuvieron lugar. Un ejemplo es el clasificación de los grupos finitos simples (también llamados el "enorme teorema"), cuya prueba entre 1955 y 1983 requiere 500 artículos de revistas y pico en cerca de 100 autores, y decenas de llenado de miles de páginas. Un grupo de matemáticos franceses, entre ellos Jean Dieudonné y André Weil, publicación bajo el seudónimo de " Nicolas Bourbaki ", intentó Exposit todas las matemáticas conocidas en su conjunto riguroso coherente. Las resultantes varias docenas de volúmenes ha tenido una influencia polémico a la educación matemática.
Geometría diferencial entró en su propio cuando Einstein utilizó en la relatividad general . Nuevas áreas enteras de las matemáticas, como la lógica matemática, topología , y John von Neumann 's teoría del juego cambiaron el tipo de preguntas que pueden ser respondidas por métodos matemáticos. Todo tipo de estructuras se resumieron mediante axiomas y nombres dados como espacios métricos, espacios topológicos etc. Como hacen los matemáticos, el concepto de una estructura abstracta en sí era abstracta y condujeron a la teoría de categorías. Grothendieck y Serre refundición geometría algebraica usando teoría de la gavilla. Grandes avances se hicieron en el estudio cualitativo de los sistemas dinámicos que Poincaré había iniciado en la década de 1890. Mida la teoría fue desarrollada a finales del siglo 19 y principios del 20. Aplicaciones de medidas incluyen la integral de Lebesgue , axiomatización de Kolmogorov de teoría de la probabilidad , y la teoría ergódica. Nudo teoría enormemente ampliado. La mecánica cuántica llevaron al desarrollo de análisis funcional. otras áreas nuevas incluyen, de Laurent Schwarz teoría de la distribución, la teoría de punto fijo, teoría de la singularidad y de René Thom teoría de las catástrofes, modelo teoría, y de Mandelbrot fractales . Acuéstese teoría con sus grupos de Lie y álgebras de Lie se convirtió en una de las principales áreas de estudio.
Análisis no estándar, introducido por Abraham Robinson, rehabillitated el enfoque al cálculo infinitesimal, que había caído en el descrédito a favor de la teoría de límites , mediante la ampliación del campo de los números reales a los números hiperreal que incluyen cantidades infinitesimales e infinitos. Un sistema de número aún mayor, los números surrealistas fueron descubiertos por John Horton Conway en conexión con juegos combinatorios.
El desarrollo y la mejora continua de los ordenadores , en primeras máquinas analógicas mecánicas y luego las máquinas electrónicas digitales, permitió la industria para hacer frente a cantidades cada vez mayores de datos para facilitar la producción y la distribución y la comunicación de masas, y se desarrollaron nuevas áreas de las matemáticas para hacer frente a este : Alan Turing 's teoría de la computabilidad, teoría de la complejidad, de Claude Shannon teoría de la información, procesamiento de señales, análisis de datos, optimización y otras áreas de la investigación de operaciones . En los siglos anteriores mucho enfoque matemático estaba en el cálculo y las funciones continuas, pero el auge de las redes informáticas y de comunicación llevó a una creciente importancia de los conceptos discretos y la expansión de la combinatoria incluyendo la teoría de grafos. Las capacidades de velocidad y procesamiento de datos de las computadoras también permitió el manejo de matemática problemas que eran demasiado tiempo para hacer frente a por cálculos de lápiz y papel, lo que lleva a las áreas tales como el análisis numérico y cálculo simbólico. Algunos de los métodos más importantes y algoritmos del siglo 20 son: el algoritmo simplex, la Transformada Rápida de Fourier, los códigos de corrección de errores, el filtro de Kalman de la teoría de control y el algoritmo RSA de criptografía de clave pública.
Al mismo tiempo, se hicieron conocimientos profundos acerca de las limitaciones a las matemáticas. En 1929 y 1930, se comprobó la veracidad o falsedad de todas las declaraciones formuladas por los números naturales más uno de la suma y multiplicación, era decidible, es decir, podría ser determinado por algún algoritmo. En 1931, Kurt Gödel descubrió que esto no fue el caso de lo natural números más tanto la suma y la multiplicación; Este sistema, conocido como la aritmética de Peano, era de hecho incompletable. (Aritmética de Peano es adecuado para una buena parte de la teoría de números , incluyendo la noción de número primo .) A consecuencia de dos de Gödel teoremas de incompletitud es que en cualquier sistema matemático que incluye la aritmética de Peano (incluyendo todos los análisis y la geometría ), la verdad sobrepasa necesariamente la prueba, es decir, no son afirmaciones verdaderas que no pueden ser probadas dentro del sistema. De ahí que las matemáticas no puede reducirse a la lógica matemática, y David Hilbert sueño 's de hacer todas las matemáticas completas y coherentes necesarias para ser reformulado.
Una de las figuras más coloridas en las matemáticas del siglo 20 fue Srinivasa Ramanujan Aiyangar (1887-1920), un indio autodidacta que conjetura o probó más de 3000 teoremas, incluidas las propiedades de los números altamente compuestos, la función de partición y sus asintótica y funciones theta simulacros . También hizo importantes investigaciones en las áreas de funciones gamma, formas modulares, series divergentes, serie hipergeométrica y número primo teoría.
Paul Erdös publicó más documentos que cualquier otro matemático en la historia, el trabajo con cientos de colaboradores. Los matemáticos tienen un juego equivalente al Juego de Kevin Bacon, que lleva a la número Erdős de un matemático. Esto describe la "distancia de colaboración" entre una persona y Paul Erdös, medida por la autoría conjunta de documentos matemáticos.
Emmy Noetherha sido descrito por muchos como la mujer más importante en la historia de las matemáticas, que revolucionó las teorías de anillos, campos, y álgebras.
Como en la mayoría de las áreas de estudio, la explosión del conocimiento en la era científica ha llevado a la especialización: a finales del siglo había cientos de áreas especializadas en matemáticas y el Mathematics Subject Classification era docenas de páginas. Más y más revistas matemáticas fueron publicados y, a finales de siglo, el desarrollo de la World Wide Web condujo a la publicación en línea.
Siglo 21
En 2000, la Clay Mathematics Institute anunció los sieteproblemas del milenio, y en 2003 laconjetura de Poincaré fue resuelto porGrigori Perelman (que se negó a aceptar un premio en este punto).
La mayoría de las revistas matemáticas ahora tienen versiones en línea, así como las versiones impresas, y se ponen en marcha muchos sólo en línea revistas. Hay una unidad cada vez mayor hacia la publicación de acceso abierto, primero popularizado por el arXiv.
Futuro de las matemáticas
Hay muchas tendencias observables en las matemáticas, el ser más notable que el tema es cada vez mayor, las computadoras son cada vez más importante y poderosa, la aplicación de las matemáticas a la bioinformática se está expandiendo rápidamente, el volumen de datos a analizar siendo producido por la ciencia y la industria, facilitado por las computadoras, está expandiendo de forma explosiva.
