Infinito

Temas relacionados: Matemáticas

Sabías ...

Voluntarios SOS ayudaron a elegir artículos e hicieron otros materiales currículo madres SOS cada mirada después de un una familia de niños apadrinados .

El símbolo del infinito, ∞, en varios tipos de letra.

Infinito (simbólicamente representado con ∞) viene de los latinos Infinitas o "infinitud". Se refiere a varios conceptos distintos (por lo general vinculados a la idea de "sin fin") que se presenten en la filosofía , las matemáticas , y teología.

En matemáticas , el "infinito" se utiliza a menudo en contextos donde es tratado como si fuera un número (es decir, cuenta o mide las cosas: "un número infinito de términos"), pero es un tipo diferente de "número" que el números reales . Infinito está relacionado con límites , números aleph, clases en la teoría de conjuntos , Conjuntos Dedekind-infinitos, grandes cardenales, La paradoja de Russell, aritmética no estándar, números hiperreales, la geometría proyectiva, números reales extendidas y la absoluta Infinito.

Historia

Los primeros puntos de vista de la India del infinito

La Isha Upanishad del Yajurveda (c. 4 al siglo 3 aC) establece que "si se quita una parte del infinito o añade una parte al infinito, aún lo que queda es infinito".

Pūrṇam Ada pūrṇam idam (Eso es completo, esto está lleno)

udacyate pūrṇam pūrṇāt (Del total, el pleno se resta)

pūrṇasya pūrṇam ādāya (Cuando el pleno se ha tomado de la completa)

evāvasiṣyate pūrṇam (El pleno aún permanecerán.) - Isha Upanishad

El indio matemática texto Surya Prajnapti (c. 400 aC) clasifica todos los números en tres conjuntos: enumerables, innumerables e infinitas. Cada uno de éstos se subdividió en tres órdenes:

Enumerable: bajo, intermedio y alto
Innumerable: casi innumerables, verdaderamente innumerables e innumerable innumerable
Infinito: casi infinita, verdaderamente infinita, infinitamente infinita

La Jainistas fueron los primeros en descartar la idea de que todos los infinitos eran el mismo o equivalente. Reconocieron diferentes tipos de infinitos: infinitas de longitud (una dimensión), infinito en el área (dos dimensiones), infinito en volumen (tres dimensiones), e infinito perpetuamente (número infinito de dimensiones).

Según Singh (1987), Joseph (2000) y Agrawal (2000), el mayor número numerable N de los jainistas se corresponde con el concepto moderno de aleph-null 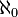$\ Aleph_0$ (El número cardinal del conjunto infinito de números enteros 1, 2, ...), el cardenal más pequeño número transfinito. El jainistas también definió todo un sistema de números cardinales infinitos, de los cuales el mayor número numerable N es el más pequeño.

En la obra Jaina en la teoría de conjuntos , dos tipos básicos de números infinitos se distinguen. Por tanto física como razones ontológicas, se hizo una distinción entre asaṃkhyāta ("incontable, innumerable") y Ananta ("sin fin, sin límites"), entre delimitada de manera rígida y poco infinitos acotadas.

Lógica

En una lógica argumento del regreso infinito es "un tipo distintivo filosófica del argumento que pretende mostrar que una tesis es defectuoso porque genera una serie infinita cuando cualquiera (forma A) no existe tal serie o (forma B) eran que exista, la tesis carecería de la papel (por ejemplo, de la justificación) que se supone que jugar ".

Símbolo del infinito

John Wallis introdujo el símbolo de infinito a la literatura matemática.

El origen exacto del símbolo del infinito "∞" no está claro. Una posibilidad es sugerido por el nombre a veces se llama la- lemniscata, desde el lemnisco latín, que significa "de la cinta". Uno puede imaginarse caminando para siempre a lo largo de un simple bucle formado a partir de una cinta.

Una explicación popular es que el símbolo de infinito se deriva de la forma de una Cinta de Moebius. Una vez más, uno puede imaginar a pie a lo largo de su superficie para siempre. Sin embargo, esta explicación es improbable, ya que el símbolo ha sido utilizado para representar el infinito durante más de doscientos años antes August Ferdinand Möbius y Johann Benedict Listing descubrió la cinta de Moebius en 1858 .

También es posible que se inspira en el más viejo religioso / alquímico simbolismo. Por ejemplo, se ha encontrado en tibetano Grabados rupestres, y el ouroboros, o infinito serpiente, es a menudo representado en esta forma.

John Wallis generalmente se le atribuye la introducción ∞ como símbolo de infinito en 1655 en su De sectionibus conicis. Una conjetura sobre por qué eligió este símbolo es que lo derivó de un número romano para 1000 que fue a su vez deriva de la Numeral etrusca de 1000, que parecía un poco como CIƆ ya veces se usa para referirse a "muchos". Otra conjetura es que él lo derivó de la letra griega ω ( omega), la última letra en el alfabeto griego .

Otra posibilidad es que el símbolo fue elegido porque era fácil de rotar un carácter "8" de 90 ° cuando composición tipográfica se hacía a mano. El símbolo es a veces llamado un "perezoso ocho", que evoca la imagen de un "8" miente en su lado.

Otra creencia popular es que el símbolo de infinito es una representación clara de la reloj de arena gira 90 °. Obviamente, esta acción puede provocar que el reloj de arena para tomar un tiempo infinito para vaciar presentando así un ejemplo tangible del infinito. La invención del reloj de arena es anterior a la existencia del símbolo de infinito permitiendo que esta teoría sea plausible.

El símbolo de infinito está representado en Unicode por el carácter ∞ (U + 221E).

Infinito matemático

Infinito se utiliza en diversas ramas de las matemáticas.

Cálculo

En análisis real, el símbolo 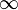$\ Infty$ , Llamado "el infinito", denota una ilimitada límite . 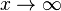$x \ rightarrow \ infty$ significa que x crece sin límite, y 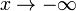$x \ rightarrow - \ infty$ significa el valor de x es decreciente sin límite. Si f (t) ≥ 0 para cada t, entonces

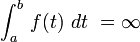$\ Int_ {a} ^ {b} \, f (t) \ dt \ = \ infty$ significa que f (t) no obligado un área finita de A a B
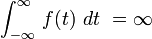$\ Int _ {- \ infty} ^ {\ infty} \, f (t) \ dt \ = \ infty$ significa que el área bajo f (t) es infinito.
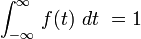$\ Int _ {- \ infty} ^ {\ infty} \, f (t) \ dt \ = 1$ significa que el área bajo f (t) es igual a 1

Infinito también se utiliza para describir serie infinita:

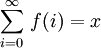$\ sum_ {i = 0} ^ {\ infty} \, f (i) = x$ significa que la suma de la serie infinita converge a un valor real x.
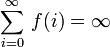$\ Sum_ {i = 0} ^ {\ infty} \, f (i) = \ infty$ significa que la suma de la serie infinita diverge en el sentido específico de que las sumas parciales crecer sin límite.

Propiedades algebraicas

Infinito se utiliza a menudo no sólo para definir un límite, sino como un valor en el sistema de números reales affinely extendida. Puntos marcado 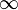$\ Infty$ y $- \ Infty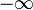$ se puede añadir a la espacio topológico de los números reales, la producción de los dos puntos compactación de los números reales. Adición de propiedades algebraicas para esto nos da los números reales extendidos. También podemos tratar 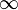$\ Infty$ y $- \ Infty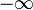$ como el mismo, que conduce a la de un punto compactación de los números reales, que es el recta proyectiva real. La geometría descriptiva también introduce un línea en el infinito en geometría plana , y así sucesivamente para las dimensiones superiores.

La recta real extendida añade dos elementos llamados infinito ( 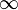$\ Infty$ ), Mayor que todos los demás números reales extendidas y menos infinito ( 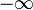$- \ Infty$ ), Menor que el resto de los números reales extendidos, para los cuales se pueden realizar algunas operaciones aritméticas.

Análisis complejo

Al igual que en el análisis real, análisis complejo el símbolo 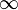$\ Infty$ , Llamado "el infinito", denota una ilimitada límite . 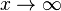$x \ rightarrow \ infty$ significa que la magnitud 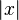$| X |$ de x crece más allá de cualquier valor asignado. La punto etiquetado 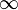$\ Infty$ se puede añadir al plano complejo como un espacio topológico dándole la de un punto compactificación del plano complejo. Cuando se hace esto, el espacio resultante es un unidimensional colector complejo, o superficie de Riemann , llamado el plano complejo extendido o la Esfera de Riemann. Las operaciones aritméticas similares a las dadas a continuación para los números reales extendidos también se pueden definir, aunque no existe una distinción en los signos (por lo tanto, es una excepción que el infinito no se puede añadir a sí mismo). Por otro lado, este tipo de infinito permite la división por cero, a saber, 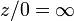$z / 0 = \ infty$ para cualquier número complejo z. En este contexto es a menudo útil tener en cuenta funciones meromorfas como mapas en la esfera de Riemann tomando el valor de 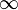$\ Infty$ en los polos. El dominio de una función de valor complejo podrá ampliarse para incluir el punto en el infinito también. Un ejemplo importante de este tipo de funciones es el grupo de Transformaciones de Möbius.

Análisis no estándar

La formulación original del cálculo por Newton y Leibniz usa cantidades infinitesimales. En el siglo XX, se ha demostrado que este tratamiento podría ser puesto en pie de rigurosa a través de varios sistemas lógicos, incluyendo análisis infinitesimal suave y análisis no estándar. En este último, los infinitesimales son invertible, y sus inversas son números infinitos. Los infinitos en este sentido son parte de un todo campo; no hay equivalencia entre ellos como con la cantoriana transfinitos. Por ejemplo, si H es un número infinito, entonces H + H = H y 2H + 1 son diferentes números infinitos.

Teoría de conjuntos

Un tipo diferente de "infinito" son la ordinales y cardinales infinitos de la teoría de conjuntos. Georg Cantor desarrollaron un sistema de números transfinitos, en el que la primera cardinal transfinito es aleph-null 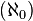$(\ Aleph_0)$ , La cardinalidad del conjunto de números naturales . Esta concepción matemática moderna del infinito cuantitativo desarrollado a finales del siglo XIX, desde el trabajo de Cantor, Gottlob Frege, Richard Dedekind y otros, utilizando la idea de colecciones, o conjuntos.

El enfoque de Dedekind era esencialmente de adoptar la idea de uno-a-uno correspondencia como un estándar para comparar el tamaño de los conjuntos, y para rechazar la vista de Galileo (que deriva de Euclides ) que el conjunto no puede ser del mismo tamaño que la parte. Un conjunto infinito simplemente puede ser definido como uno que tiene el mismo tamaño que al menos uno de sus " propios "partes; esta noción de infinito se llama Dedekind infinito.

Cantor definió dos tipos de números infinitos, los números ordinales y la números cardinales. Los números ordinales se pueden identificar con conjuntos bien ordenada, o conteo realizado a cualquier punto de parada, incluidos los puntos después de un número infinito ya han sido contados. Generalizando finito y lo infinito ordinaria secuencias que son mapas de los positivos enteros conduce a asignaciones de números ordinales, y secuencias transfinitos. Los números cardinales definen el tamaño de los conjuntos, es decir cuántos miembros que contienen, y pueden ser estandarizados por elegir el primer número ordinal de un cierto tamaño para representar el número cardinal de ese tamaño. El más pequeño infinito ordinal es la de los números enteros positivos, y cualquier conjunto que tiene la cardinalidad de los números enteros es infinito numerable. Si en el conjunto es demasiado grande para ser puesto en correspondencia uno a uno con los enteros positivos, se llama incontable. vistas de Cantor prevalecieron y la matemática moderna acepta infinito actual. Ciertos extendidos número de sistemas, tales como el números hiperreales, incorporan los números ordinarios (finitos) y un número infinito de diferentes tamaños.

Nuestra intuición adquirida conjuntos finitos se rompe cuando se trata de conjuntos infinitos. Un ejemplo de esto es El hotel infinito de Hilbert.

La cardinalidad del continuo

Uno de los resultados más importantes de Cantor fue que el cardinalidad del continuo ( 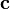$\ Mathbf c$ ) Es mayor que la de los números naturales ( 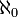${\ Aleph_0}$ ); es decir, hay más números reales R de los números naturales N. Es decir, Cantor mostró que 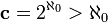$\ Mathbf {c} = 2 ^ {\ aleph_0}> {\ aleph_0}$ (Ver Argumento diagonal de Cantor).

La hipótesis del continuo establece que no hay número cardinal entre la cardinalidad de los números reales y la cardinalidad de los números naturales, es decir, 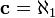$\ Mathbf {c} = \ aleph_1$ . Sin embargo, esta hipótesis puede ser probada ni refutada en el ampliamente aceptado Axiomas de Zermelo-Fraenkel, aun suponiendo que el Axioma de elección.

Cardenal aritmética se puede utilizar para mostrar no sólo que el número de puntos en una línea número real es igual al número de puntos en cualquier segmento de esa línea, pero que este es igual al número de puntos en un plano y, de hecho, en cualquier espacio de dimensión finita. Estos resultados son muy contrario a la intuición, porque implican que existen subconjuntos propios de un conjunto S infinita que tiene el mismo tamaño que S.

El primero de estos resultados es evidente al considerar, por ejemplo, la tangente función, que proporciona una uno-a-uno correspondencia entre la intervalo [-0.5π, 0.5π] y R (véase también El hotel infinito de Hilbert). El segundo resultado fue probado por Cantor en 1878, pero sólo llegó a ser intuitivamente evidente en 1890, cuando Giuseppe Peano introdujo el curvas que llenan el espacio, las líneas curvas que girar y girar lo suficiente para llenar la totalidad de cualquier cuadrado, o cubo, o hipercubo, o espacio de dimensión finita. Estas curvas se pueden utilizar para definir una uno-a-uno entre los puntos en el lado de un cuadrado y las de la plaza.

También es posible mostrar que los conjuntos con cardinalidad estrictamente mayor que 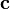$\ Mathbf c$ existir. Ellos incluyen, por ejemplo:

el conjunto de todos los subconjuntos de R, es decir, el conjunto potencia de R, P escrito (R) o 2 ^R
el conjunto R ^R de todas las funciones de R a R

Ambos tienen cardinalidad 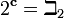$2 ^ \ mathbf {c} = \ beth_2$ (Ver Número Bet).

Matemáticas sin el infinito

Leopold Kronecker rechazó la noción de infinito y comenzó una escuela de pensamiento, en el filosofía de las matemáticas llamada finitismo que influyó en la escuela filosófica y matemática de constructivismo matemático.

Infinito Física

En la física , aproximaciones de números reales se utilizan para mediciones continuas y números naturales se utilizan para mediciones discretas (es decir, de conteo). Por lo tanto, se asume por los físicos que no cantidad mensurable podría tener un valor infinito, por ejemplo mediante la adopción de un valor infinito en una sistema de números reales de tiempo (consulte también: número hiperreal), o al exigir el recuento de un número infinito de eventos. Está por ejemplo presunta imposible para cualquier cuerpo tenga masa infinita o energía infinita. Existe el concepto de entidades infinitas (tales como un infinito onda plana), pero no hay modo de producir este tipo de cosas.

Cabe señalar que esta práctica de negarse valores infinitos para cantidades medibles no viene de a priori o motivaciones ideológicas, sino de las motivaciones más metodológicas y pragmáticas. Una de las necesidades de cualquier teoría física y científica es dar fórmulas utilizables que se corresponden con la realidad o por lo menos aproximada. Como ejemplo, si un objeto de masa gravitacional infinita fuera a existir, cualquier uso de la fórmula para calcular la fuerza gravitacional conduciría a un resultado infinito, lo que sería de ningún beneficio ya que el resultado sería siempre la misma independientemente de la posición y la masa del otro objeto. La fórmula sería útil ni para calcular la fuerza entre dos objetos de masa finita ni para calcular sus movimientos. Si un objeto de masa infinita fuera a existir, cualquier objeto de masa finita sería atraído con fuerza infinita (y por tanto la aceleración) por el objeto de masa infinita, que no es lo que podemos observar en la realidad.

Este punto de vista no significa que el infinito no se puede utilizar en la física. Por el amor, cálculos, ecuaciones, teorías y aproximaciones de conveniencia a menudo usan serie infinita, sin límites funciones , etc., y puede hacerse por cantidades infinitas. Los físicos, sin embargo requieren que el resultado final sea físicamente significativa. En la teoría cuántica de campo infinitos surgir que deben interpretarse de manera tal que conduzca a un resultado con significado físico, un proceso conocido como renormalización . Una aplicación en la que surgen infinitos es la cuantificación de temperaturas termodinámicas .

Sin embargo, hay algunas circunstancias actualmente aceptados en el que el resultado final es el infinito. Un ejemplo es un agujero negro . Los físicos han comprobado que, cuando una estrella experiencias colapso gravitacional, con el tiempo se reducirá hasta un punto de tamaño cero, y por lo tanto tienen una densidad infinita. Este es un ejemplo de lo que se llama una singularidad matemática, o un punto en que las leyes de las matemáticas, y por lo tanto de la física, se descomponen. Algunos físicos creen ahora que la singularidad puede ser física real, y desde entonces han centrado su atención en la búsqueda de nuevas matemáticas donde infinitos son posibles.

Infinito en la cosmología

Una pregunta interesante es si existe infinito actual en nuestro físico universo hay infinitas estrellas:? ¿El universo tiene volumen infinito? ¿Tiene espacio "continuar para siempre"? Esta es una importante pregunta abierta de la cosmología . Tenga en cuenta que la cuestión del ser infinito es lógicamente independiente de la cuestión de tener límites. La superficie bidimensional de la Tierra, por ejemplo, es finito, sin embargo, no tiene borde. Por caminar / vela / recto el tiempo suficiente, volverá al punto exacto se empezó. El universo, al menos en principio, podría tener un parecido topología ; si que volar tu nave espacial hacia el frente lo suficiente, tal vez con el tiempo podría volver a su punto de partida. Sin embargo, si el universo se está expandiendo siempre , entonces nunca podría volver a su punto de partida, incluso a una escala de tiempo infinito.

Representaciones informáticos del infinito

La IEEE estándar de punto flotante especifica valores infinito positivo y negativo; estos pueden ser el resultado de desbordamiento aritmético, división por cero, u otras operaciones excepcionales.

Algunos lenguajes de programación (por ejemplo, J y UNIDAD) especificar mayor y menos elementos, es decir, valores que comparar (respectivamente) mayor que o menor que todos los demás valores. Estos también pueden denominarse parte superior e inferior, o más infinito y menos infinito; que son útiles como valores centinela en algoritmos que involucran clasificación, búsqueda o de ventanas. En lenguajes que no tienen mayores y menos elementos, pero no permitir que sobrecarga de operadores relacionales, es posible crear más grandes y menos elementos (con alguna gastos generales, y el riesgo de incompatibilidad entre implementaciones).

Perspectiva y puntos en el infinito en las artes

Obra Perspectiva utiliza el concepto de imaginario puntos de fuga, o puntos del infinito, situado a una distancia infinita del observador. Esto permite a los artistas crear pinturas que 'realista' representan la distancia y el escorzo de objetos. Artista MC Escher se conoce específicamente para emplear el concepto de infinito en su trabajo en este y otros aspectos.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Infinity&oldid=198896642 "

We provide Linux to the World