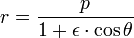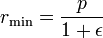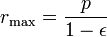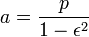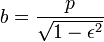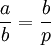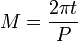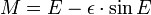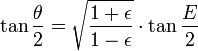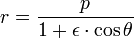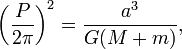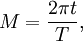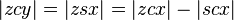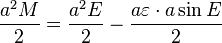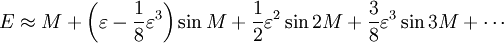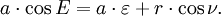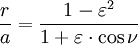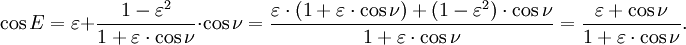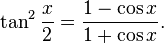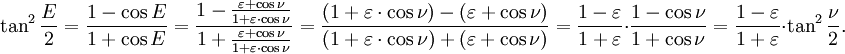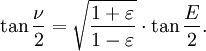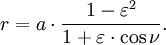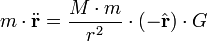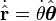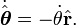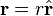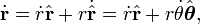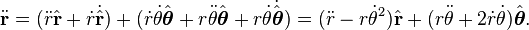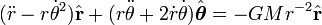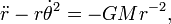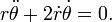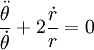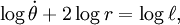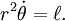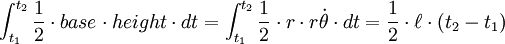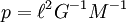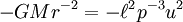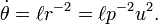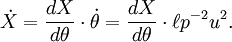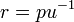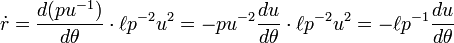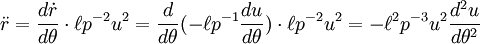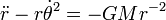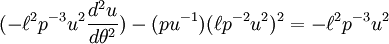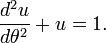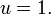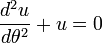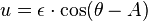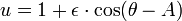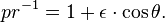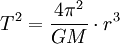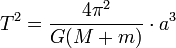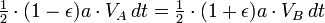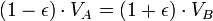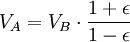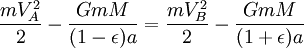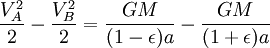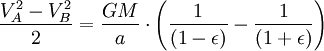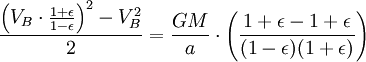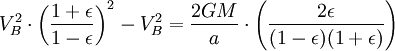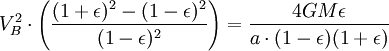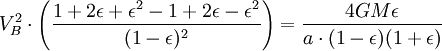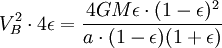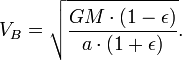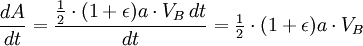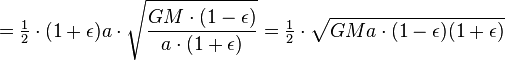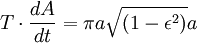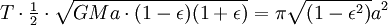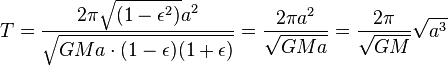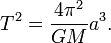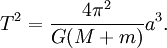Leyes de Kepler

Temas relacionados: Matemáticas

Antecedentes

SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. Haga clic aquí para obtener información sobre el apadrinamiento de niños.

Ilustración de tres leyes de Kepler con dos órbitas planetarias. (1) Las órbitas son elipses, con puntos focales f1 y f2 para el primer planeta y f1 y f3 para el segundo planeta. El sol se pone en el punto focal f1. (2) Los dos sectores sombreados A1 y A2 tienen la misma área de superficie y el tiempo para el planeta 1 para cubrir segmento A1 es igual al tiempo para cubrir segmento A2. 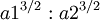(3) Los tiempos totales de órbita para el planeta y el planeta 1 2 tienen una relación $a1 ^ {3/2}: a2 ^ {3/2}$ .

En astronomía , leyes de movimiento planetario de Kepler son tres leyes matemáticas que describen el movimiento de los planetas en el Sistema Solar . Alemán matemático y el astrónomo Johannes Kepler ( 1571- 1630) las descubrieron.

Kepler estudió el observaciones del astrónomo danés precisa legendariamente Tycho Brahe. Alrededor de 1605, Kepler descubrió que las observaciones de Brahe de las posiciones de los planetas siguieron tres leyes matemáticas relativamente simples.

Las leyes de Kepler desafiaron la astronomía y la física aristotélica y ptolemaica. Su afirmación de que la Tierra se movía, su uso de puntos suspensivos en lugar de epiciclos, y su prueba de que las velocidades de los planetas varían, cambian la astronomía y la física . Sin embargo, la explicación física de la conducta de los planetas llegó casi un siglo más tarde, cuando Isaac Newton fue capaz de deducir las leyes de Kepler de las propias de Newton leyes del movimiento y su la ley de la gravitación universal, utilizando su invención del cálculo . Otros modelos de la gravitación darían resultados empíricamente falsas.

Tres leyes de Kepler son:

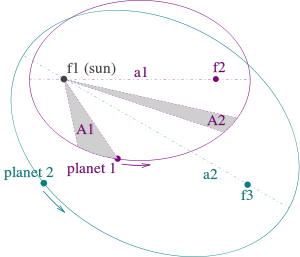
La órbita de cada planeta es una elipse con el Sol en uno de los focos. Una elipse se caracteriza por sus dos puntos focales; vea la ilustración. Así, Kepler rechazó la antigua aristotélica, de Ptolomeo, Copérnico y la creencia en el movimiento circular.
Una línea de unirse a un planeta y el Sol barre áreas iguales en tiempos iguales como el planeta se desplaza a lo largo de su órbita. Esto significa que el planeta viaja más rápido, mientras que cerca del sol y reduce la velocidad cuando se está más lejos del sol. Con su ley, Kepler destruido la teoría astronómica aristotélica de que los planetas tienen uniforme velocidad .
La plazas de la períodos orbitales de los planetas son directamente proporcional a la cubos de la semi-ejes principales (el "de longitud media" de la elipse) de sus órbitas. Esto significa no sólo que las órbitas más grandes tienen períodos más largos, sino también que la velocidad de un planeta en una órbita más grande es menor que en una órbita más pequeña.

Las leyes de Kepler se formulan a continuación, y se derivan de las leyes de Newton, usando heliocéntricas coordenadas polares 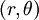$\ (R, \ theta)$ . Sin embargo, las leyes de Kepler, alternativamente, se pueden formular y derivados utilizando coordenadas cartesianas .

Descripción matemática

Primera ley

La primera ley de Kepler

La primera ley dice: "El órbita de cada planeta es una elipse con el Sol en uno de los focos ".

La matemática de la elipse es el siguiente.

La ecuación es

$r = \ frac {p} {1+ \ epsilon \ cdot \ cos \ theta}$

donde (r, θ) son las coordenadas polares heliocéntricas para el planeta, p es el recto semi-latus , y ε es el excentricidad, que es mayor que o igual a cero y menor que uno.

Para θ = 0, el planeta está en el perihelio a una distancia mínima de:

$r_ \ mathrm {min} = \ frac {p} {1+ \ epsilon}$

para θ = 90 °: r = p, y para θ = 180 ° del planeta está en el afelio a la máxima distancia:

$r_ \ mathrm {max} = \ frac {p} {1- \ epsilon}$

La semi-eje mayor es la media aritmética entre r _min y r _max:

$a = \ frac {p} {1- \ epsilon ^ 2}$

La semi-eje menor es la media geométrica entre r _min y r _max:

$b = \ frac {p \ sqrt {1- \ epsilon ^ 2}}$

y también la es media geométrica entre el semieje mayor y el recto semi latus:

$\ Frac a b = \ frac b p$

Segunda ley

Ilustración de la segunda ley de Kepler.

La segunda ley: "Una línea de unirse a un planeta y el Sol barre áreas iguales en tiempos iguales. "

Esto también se conoce como la ley de áreas iguales. Es una consecuencia directa de la ley de conservación del momento angular ; ver la derivación a continuación.

Supongamos que un planeta tarda un día para viajar de punto A a B. Las líneas desde el Sol a A y B, junto con la órbita del planeta, definirán un (más o menos triangular área). Esta misma cantidad de área se formará cada día sin importar donde en su órbita el planeta es. Esto significa que el planeta se mueve más rápido cuando se está más cerca del sol.

Esto se debe a la gravedad del sol acelera el planeta a medida que cae hacia el sol, y se desacelera en el camino de vuelta, pero Kepler no sabía eso.

Las dos leyes permitieron a Kepler para calcular la posición, (r, θ), del planeta, basados en el tiempo transcurrido desde perihelio, t, y el período orbital, P. El cálculo se realiza en cuatro pasos.

1. Calcular la anomalía media M de la fórmula

$M = \ frac {2 \ pi t} {P}$

2. Calcular el excéntrica anomalía E resolviendo numéricamente la ecuación de Kepler:

$\ M = E \ epsilon \ cdot \ pecado E$

3. Calcular el verdadera θ anomalía por la ecuación:

$\ Tan \ frac \ theta 2 = \ sqrt {\ frac {1+ \ epsilon} {1- \ epsilon}} \ cdot \ tan \ frac E 2$

4. Calcule la distancia r heliocéntrica de la primera ley:

$r = \ frac {p 1+ \ epsilon \ cdot \ cos \ theta}$

La prueba de este procedimiento se muestra a continuación.

Tercera ley

La tercera ley: "El plazas de la períodos orbitales de los planetas son directamente proporcional a la cubos de la semieje mayor de las órbitas. "Por lo tanto, no sólo la longitud de la órbita aumenta con la distancia, la velocidad orbital disminuye, por lo que el aumento de la período orbital es más que proporcional.

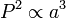
$P ^ 2 \ propto a ^ 3$

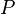$P$ = Período orbital de planeta

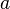$un$ = Semieje mayor de la órbita

Así que la expresión de P ² · un ^-3 tiene el mismo valor para todos los planetas del Sistema Solar , ya que tiene para la Tierra . Cuando se eligen ciertas unidades, es decir, P se mide en año sideral y una en unidades astronómicas, P ² · un ^-3 tiene el valor 1 para todos los planetas del Sistema Solar.

En Unidades del SI: 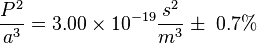$\ Frac {P ^ {2}} {a ^ {3}} = 3,00 \ times 10 ^ {- 19} \ frac {s ^ {2}} {m ^ {3}} \ pm \ 0,7% \,$ .

La ley, cuando se aplica a órbitas circulares, donde la aceleración es proporcional a una · P ^-2, muestra que la aceleración es proporcional a una · un ^-3 = a ^-2, de conformidad con La ley de Newton de la gravitación.

La ecuación general, que Kepler no lo sabía, es

$\ Left ({\ frac {P} {2 \ pi}} \ right) ^ 2 = {a ^ 3 \ over G (M + m)},$

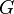donde $G$ es la constante gravitacional, 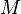$M$ es la masa del Sol, y 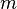$m$ es la masa del planeta. Este último aparece en la ecuación ya que la ecuación de movimiento implica el reducción de la masa. Tenga en cuenta que P es el tiempo por órbita y P / 2π es momento por radián .

Ver las cifras reales: atributos de los planetas mayores.

Esta ley también se conoce como la ley armónica.

Posición como una función del tiempo

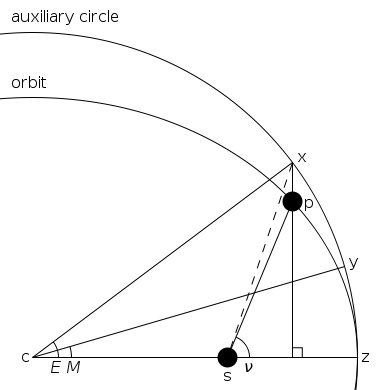
El problema kepleriano asume un órbita elíptica y los cuatro puntos:

s el sol (en uno de los focos de la elipse);
z el perihelio
c el centro de la elipse
p el planeta

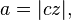$\ A = | cz |,$ distancia desde el centro hacia el perihelio, el semieje mayor,

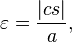$\ \ Varepsilon = {| cs | \ over a},$ la excentricidad,

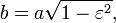$\ B = a \ sqrt {1- \ varepsilon ^ 2},$ los semieje menor,

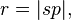$\ R = | sp |,$ la distancia del sol en planeta.

y el ángulo

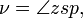$\ Nu = \ zsp ángulo,$ el planeta visto desde el sol, la anomalía verdadera.

El problema consiste en calcular las coordenadas polares (r, ν) del planeta desde el tiempo transcurrido desde el perihelio, t.

Se resuelve en pasos. Kepler comenzó mediante la adición de círculo auxiliar de la órbita (que con el eje mayor como diámetro) y define estos puntos:

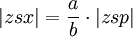
x es la proyección del planeta al círculo auxiliar; entonces el área $| ZSX | = \ frac una b \ cdot | zsp |$
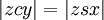
y es un punto en el círculo auxiliar tal que el área $\ | Zcy | = | ZSX |$

$M = \ zcy ángulo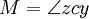$ , Y como se ve desde el centro, el anomalía media.

El área de la sector circular 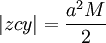$\ | Zcy | = \ frac {a ^ 2 M 2}$ , Y el área barrida desde el perihelio,

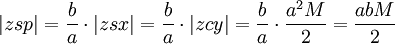$| Zsp | = \ frac ba \ cdot | ZSX | = \ frac ba \ cdot | zcy | = \ frac ba \ cdot \ frac {a ^ 2} M 2 = \ frac {ab M} {2}$ ,

es por segunda proporcional ley de Kepler en cuando desde el perihelio. Así que la anomalía media, M, es proporcional al tiempo transcurrido desde el perihelio, t.

$M = {2 \ pi t \ over T}$

donde T es el período orbital.

La anomalía media M se calcula en primer lugar. El objetivo es calcular la verdadera ν anomalía. La función ν = f (M) es, sin embargo, no elemental. Solución de Kepler es utilizar

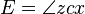$E = \ zcx ángulo$ , X como se ve desde el centro, el anomalía excéntrica

como una variable intermedia, y primero compute E como una función de M mediante la resolución de la ecuación de Kepler a continuación, y luego calcular la anomalía verdadera ν de la anomalía excéntrica E. Aquí están los detalles.

$\ | Zcy | = | ZSX | = | zcx | - | scx |$

$\ Frac {a ^ 2} M 2 = \ frac {a ^ 2 E} 2- \ frac {a \ varepsilon \ cdot un \ pecado E} 2$

División por un ² / 2 da la ecuación de Kepler

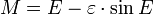$M = E \ varepsilon \ cdot \ pecado E$ .

El problema es que la ecuación de Kepler no puede ser reorganizado para aislar E. La función E = f (M) no es una fórmula elemental. La ecuación de Kepler se resuelve iterativamente ya sea por una Resolución numérica de ecuaciones no lineales o, como se deriva en el artículo sobre anomalía excéntrica, por una serie infinita

$E \ aprox M + \ left (\ varepsilon- \ frac18 \ varepsilon ^ 3 \ right) \ pecado M + \ frac12 \ varepsilon ^ 2 \ sin 2M + \ frac38 \ varepsilon ^ 3 \ pecado 3M + \ cdots$

Para el pequeño ε típico de los planetas (excepto Plutón ), dichas series son bastante precisa con sólo unos pocos términos.

Habiendo calculado la anomalía excéntrica E de la ecuación de Kepler, el siguiente paso es calcular la anomalía verdadera ν de la anomalía excéntrica E.

Nota de la geometría del problema que

$a \ cdot \ cos E = a \ cdot \ varepsilon + r \ cdot \ cos \ nu.$

Dividiendo por una y la inserción de la primera ley de Kepler

$\ \ Frac ra = \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}$

llegar

$\ Cos E = \ varepsilon + \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu} \ cdot \ cos \ nu = \ frac {\ varepsilon \ cdot (1+ \ varepsilon \ cdot \ cos \ nu) + (1- \ varepsilon ^ 2) \ cdot \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu} = \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}.$

El resultado es una relación utilizable entre la anomalía excéntrica E y el verdadero ν anomalía.

Una forma computacionalmente más conveniente sigue sustituyendo en el identidad trigonométrica:

$\ Tan ^ 2 \ frac {x} {2} = \ frac {1- \ cos x} {1+ \ cos x}.$

Llegar

$\ Tan ^ 2 \ frac {E} {2} = \ frac {1- \ cos E} {1+ \ cos E} = \ frac {1- \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} {1+ \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} = \ frac {(1+ \ varepsilon \ cdot \ cos \ nu) - (\ varepsilon + \ cos \ nu)} {(1+ \ varepsilon \ cdot \ cos \ nu) + (\ varepsilon + \ cos \ nu)} = \ frac {1- \ varepsilon} {1+ \ varepsilon} \ cdot \ frac {1- \ cos \ nu} {1+ \ cos \ nu} = \ frac {1- \ varepsilon} {1+ \ varepsilon} \ cdot \ tan ^ 2 \ frac {\ nu} {2}.$

Multiplicando por (1 + ε) / (1-ε) y tomando la raíz cuadrada da el resultado

$\ Tan \ frac \ nu2 = \ sqrt \ frac {1+ \ varepsilon} {1- \ varepsilon} \ cdot \ tan \ frac E2.$

Hemos completado el tercer paso en la conexión entre el tiempo y la posición en la órbita.

Incluso se podría desarrollar una serie de computación ν directamente de M.

El cuarto paso es calcular la distancia r heliocéntrica de la verdadera ν anomalía por la primera ley de Kepler:

$\ R = a \ cdot \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}.$

Derivación de las leyes de Newton

Las leyes de Kepler son sobre el movimiento de los planetas alrededor del sol, mientras que las leyes de Newton son más generalmente sobre el movimiento de las partículas puntuales atraerse entre sí por la fuerza de la gravitación . En el caso especial en que sólo hay dos partículas, y una de ellas es mucho más ligero que el otro, y la distancia entre las partículas sigue siendo limitada, entonces la partícula se mueve más claras alrededor de la partícula pesada como un planeta alrededor del sol de acuerdo con las leyes de Kepler , como se muestra abajo. Las leyes de Newton sin embargo también admiten otras soluciones, en donde la trayectoria de la partícula más ligero es una parábola o una hipérbola. Estas soluciones muestran que hay una limitación a la aplicabilidad de la primera ley de Kepler, que establece que la trayectoria siempre será una elipse. En el caso de que una partícula no es mucho más ligero que el otro, resulta que cada partícula se mueve alrededor de su común centro de masa , por lo que el general dos problema cuerpo se reduce al caso especial donde una partícula es mucho más ligero que el otro. Si bien las leyes de Kepler se expresan en lenguaje geométrico o como ecuaciones que conectan las coordenadas del planeta y la variable tiempo con la elementos orbitales, la segunda ley de Newton es una ecuación diferencial . Así las derivaciones inferiores implican el arte de resolver ecuaciones diferenciales. La segunda ley se deriva en primer lugar, como la derivación de la primera ley depende de la derivación de la segunda ley.

Derivación de la segunda ley de Kepler

La ley de la gravitación de Newton dice que "cada objeto en el universo atrae a todos los demás objetos a lo largo de una línea de los centros de los objetos, de forma proporcional a la masa de cada objeto, e inversamente proporcional al cuadrado de la distancia entre los objetos", y su segunda ley de movimiento dice que "la masa por la aceleración es igual a la fuerza". Así la masa de los tiempos planeta el vector aceleración del planeta es igual a la masa de los tiempos dom la masa del planeta, dividido por el cuadrado de la distancia, los tiempos menos el radial vector unitario, los tiempos de una constante de proporcionalidad. Esto está escrito:

$m \ cdot \ ddot \ mathbf {r} = \ frac {M \ cdot m} {r ^ 2} \ cdot (- \ hat {\ mathbf {r}}) \ cdot G$

donde un punto en la parte superior de la variable significa la diferenciación con respecto al tiempo, y el segundo punto indica la segunda derivada.

Supongamos que el planeta es mucho más ligero que el sol que la aceleración del sol puede ser descuidado.

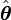$\ Dot \ hat {\ mathbf {r}} = \ dot \ theta \ hat {\ boldsymbol \ theta}$

donde $\ Hat {\ boldsymbol \ theta}$ es el vector unitario tangencial, y

$\ Dot \ hat {\ boldsymbol \ theta} = - \ dot \ theta \ hat {\ mathbf {r}}.$

Así el vector de posición

$\ Mathbf {r} = r \ hat {\ mathbf {r}}$

se diferencia dos veces para dar el vector de velocidad y el vector de aceleración

$\ Dot \ mathbf {r} = \ dot r \ hat \ mathbf {r} + r \ dot \ hat \ mathbf {r} = \ dot r \ hat {\ mathbf {r}} + r \ dot \ theta \ hat {\ boldsymbol \ theta},$

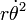$\ Ddot \ mathbf {r} = (\ ddot r \ hat {\ mathbf {r}} + \ dot r \ dot \ hat {\ mathbf {r}}) + (\ dot r \ dot \ theta \ hat {\ boldsymbol \ theta} + r \ ddot \ theta \ hat {\ boldsymbol \ theta} + r \ dot \ theta \ dot \ hat {\ boldsymbol \ theta}) = (\ ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta}.$

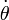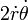Tenga en cuenta que para la distancia constante, $\ R$ , El planeta está sujeto a la aceleración centrípeta , $r \ dot \ theta ^ 2$ Y para la velocidad angular constante, $\ Dot \ theta$ , El planeta está sujeto a la aceleración de Coriolis, $2 \ dot r \ dot \ theta$ .

Inserción del vector aceleración en las leyes de Newton, y dividiendo por m, da el vector ecuación de movimiento

$(\ Ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta} = -GMr ^ {- 2} \ hat {\ mathbf {r}}$

Igualando componente, obtenemos las dos ecuaciones diferenciales ordinarias de movimiento, uno para la aceleración radial y uno para la aceleración tangencial:

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2},$

$r \ ddot \ theta + 2 \ dot r \ dot \ theta = 0.$

Con el fin de obtener la segunda ley de Kepler sólo se necesita la ecuación de la aceleración tangencial. Dividirlo por 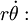$\ R \ dot \ theta:$

$\ Frac {\ ddot \ theta} {\ dot \ theta} 2 \ frac {\ dot r} {r} = 0$

e integrar:

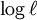$\ Log \ dot \ theta 2 \ log r = \ log \ ell,$

donde $\ Log \ ell$ es un constante de integración, y exponenciar:

$r ^ 2 \ dot \ theta = \ ell.$

Esto dice que la momento angular específica 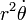$r ^ 2 \ dot \ theta$ es un constante de movimiento, incluso si tanto la distancia $\ R$ y la velocidad angular 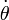$\ Dot \ theta$ variar.

El área barrida de vez en cuando t ₁ t _2,

$\ \ Int_ {t_1} ^ {t_2} \ frac 1 2 \ cdot altura de la base \ cdot \ cdot dt = \ {int_ t_1} ^ {t_2} \ frac 1 2 \ cdot r \ cdot r \ dot \ theta \ cdot dt = \ frac 1 2 \ cdot \ ell \ cdot (t_2-t_1)$

depende sólo de la duración t ₂ - t _1. Esta es la segunda ley de Kepler.

Derivando la primera ley de Kepler

La expresión

$p = \ ell ^ 2 G ^ {- 1} M ^ {- 1}$

tiene la dimensión de la longitud y se utiliza para hacer las ecuaciones de movimiento adimensional. Definimos

$\ U = pr ^ {- 1}$

y obtener

$-GMr ^ {- 2} = - \ ell ^ 2 p ^ {- 3} u ^ {2}$

$\ \ Dot \ theta = \ ell r ^ {- 2} = \ ell p ^ {- 2} u ^ 2.$

La diferenciación con respecto al tiempo se transforma en la diferenciación con respecto al ángulo:

$\ \ El punto X = \ frac {dx} {d \ theta} \ cdot \ dot \ theta = \ frac {dx} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ 2.$

Diferenciar

$\ R = pu ^ {- 1}$

dos veces:

$\ El punto r = \ frac {d (pu ^ {- 1})} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = -pu ^ {- 2} \ frac {du} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = - \ ell p ^ {- 1} \ frac {du} {d \ theta}$

$\ Ddot r = \ frac {d \ dot r} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = \ frac {d} {d \ theta} (- \ ell ^ p { -1} \ frac {du} {d \ theta}) \ cdot \ ell p ^ {- 2} u ^ {2} = - \ ell ^ 2 p ^ {- 3} u ^ {2} \ frac {d ^ 2 u} {d \ theta ^ 2}$

Sustituye en la ecuación radial de movimiento

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2}$

y obtener

$(- \ Ell ^ 2 p ^ {- 3} u ^ 2 \ frac {d ^ 2u} {d \ theta ^ 2}) - (pu ^ {- 1}) (\ ell p ^ {- 2} u ^ 2) ^ 2 = - \ ell ^ 2 p ^ {- 3} u ^ 2$

Dividido por 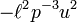$- \ Ell ^ 2 p ^ {- 3} u ^ 2$ para conseguir una sencilla ecuación diferencial lineal no homogénea de la órbita del planeta:

$\ Frac {d ^ 2u} {d \ theta ^ 2} + u = 1.$

Una solución obvia a esta ecuación es la órbita circular

$\ U = 1.$

Otras soluciones se obtienen mediante la adición de soluciones a la ecuación diferencial lineal homogénea con coeficientes constantes

$\ Frac {d ^ 2u} {d \ theta ^ 2} + u = 0$

Estas soluciones son

$\ U = \ epsilon \ cdot \ cos (\ theta-A)$

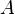donde $\ \ Epsilon$ y $\ A$ son constantes arbitrarias de la integración. Así, el resultado es

$\ U = 1 + \ epsilon \ cdot \ cos (\ theta-A)$

Elegir el eje de la tal sistema de coordenadas que 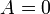$\ A = 0$ Y la inserción de 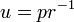$\ U = pr ^ {- 1}$ , Se obtiene:

$\ Pr ^ {- 1} = 1 + \ epsilon \ cdot \ cos \ theta.$

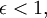Si $\ \ Epsilon <1,$ esta es la primera ley de Kepler.

La tercera ley de Kepler

Newton utilizó la tercera ley como uno de los elementos de prueba que se utilizan para construir el marco conceptual y matemático de la Ley de la Gravitación. Si tomamos las leyes del movimiento de Newton como un hecho, y consideramos un hipotético planeta que pasa a estar en una órbita perfectamente circular de radio r, entonces tenemos 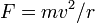$F = mv ^ 2 / r$ por la fuerza del sol en el planeta. La velocidad es proporcional a r / T, que por la tercera ley de Kepler varía como uno más de la raíz cuadrada de r. Sustituyendo esto en la ecuación de la fuerza, nos encontramos con que la fuerza de la gravedad es proporcional a uno sobre r al cuadrado. Cadena histórica real de Newton de razonamiento no se conoce con certeza, porque en su escritura tendía a borrar cualquier rastro de cómo había llegado a sus conclusiones. La inversión del sentido de razonamiento, podemos considerar esto como una prueba de la tercera ley de Kepler basado en la ley de la gravedad, y el cuidado de los factores de proporcionalidad que fueron descuidados en el argumento anterior de Newton, tenemos:

$T ^ 2 = \ frac {4 \ pi ^ 2} {GM} \ cdot r ^ 3$

donde:

T = planeta de periodo sideral
r = radio de la órbita circular del planeta
G = el constante gravitacional
M = masa del Sol

Los mismos argumentos se pueden aplicar a cualquier objeto en órbita cualquier otro objeto. Esta discusión asume implícitamente que el planeta orbita alrededor del Sol estacionario, aunque en realidad tanto el planeta y el Sol giran alrededor de su centro de masa común. Newton reconoció esto, y modificó esta tercera ley, señalando que el período también se ve afectada por el cuerpo en órbita masa . Sin embargo normalmente el cuerpo central es mucho más masiva que la masa del cuerpo en órbita puede ser ignorada. Newton también demostró que en el caso de una órbita elíptica, la semimayor eje podría ser sustituido por el radio. El resultado más general es:

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} \ cdot a ^ 3$

donde:

T = objeto de periodo sideral
a = objeto del semieje mayor
G = el constante gravitacional = 6,67 × 10 ^-11 N • m² / kg²
M = masa de un objeto
m = masa del otro objeto

Para los objetos que orbitan alrededor del sol, puede ser conveniente utilizar unidades de año, la Unión Africana, y masas solares, por lo que G, 4π² y los diversos factores de conversión se cancelan. También con m << M podemos establecer m + M = M, así que tenemos simplemente 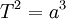$T ^ 2 = a ^ 3$ . Tenga en cuenta que los valores de G y masas planetarias no se conocen con buena precisión; Sin embargo, los productos transgénicos (la atracción kepleriano) son conocidos por una precisión extremadamente alta.

Definir el punto A al ser el periapsis, y el punto B como la apoapsis del planeta al orbitar el sol.

La segunda ley de Kepler establece que el cuerpo orbitando barrerá áreas iguales en cantidades iguales de tiempo. Si ahora miramos unos muy pequeños períodos de tiempo en los momentos en que el planeta se encuentra en los puntos A y B, entonces podemos aproximar el área barrida como un triángulo con una altura igual a la distancia entre el planeta y el sol, y la base igual a la vez que la velocidad del planeta.

$\ Begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot (1- \ epsilon) a \ cdot V_A \, dt = \ begin {matriz} \ frac {1} {2} \ end { matriz} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt$

$(1- \ epsilon) \ cdot V_A = (1+ \ epsilon) \ cdot V_B$

$V_A = V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon}$

Usando el ley de la conservación de la energía para la energía total del planeta en los puntos A y B,

$\ Frac {mV_A ^ 2} {2} - \ frac {} {GmM (1- \ epsilon) a} = \ frac {mV_B ^ 2} {2} - \ frac {} {GmM (1+ \ epsilon) un }$

$\ Frac {V_A ^ 2} {2} - \ frac {V_B ^ 2} {2} = frac {GM} {(1- \ epsilon) a} \ - \ frac {GM} {(1+ \ epsilon) un }$

$\ Frac {V_A ^ 2-V_B ^ 2} {2} = \ frac {GM} {a} \ cdot \ left (\ frac {1} {(1- \ epsilon)} - \ frac {1} {(1 + \ epsilon)} \ right)$

$\ Frac {\ dejó (V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2} {2} = \ frac {GM} {a} \ cdot \ left ( \ frac {1+ \ epsilon-1 + \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2 = \ {a} \ cdot \ left (\ frac frac {2GM} {2 \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {(1+ \ epsilon) ^ 2- (1- \ epsilon) ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot \ left (\ frac {1 + 2 \ epsilon + \ epsilon ^ 2-1 + 2 \ epsilon \ epsilon ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot 4 \ epsilon = \ frac {4GM \ epsilon \ cdot (1- \ epsilon) ^ 2} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B = \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}}.$

Ahora que tenemos 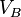$V_B$ , Podemos encontrar la velocidad a la que el planeta está barriendo a cabo en el área de la elipse. Esta tasa se mantiene constante, por lo que podemos deducir que desde cualquier punto que queremos, específicamente desde el punto B.

$\ Frac {dA} {dt} = \ frac {\ frac {1} {2} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt} {dt} = \ begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot (1+ \ epsilon) a \ cdot V_B$

$= \ Begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot (1+ \ epsilon) a \ cdot \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}} = \ begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot \ sqrt {GMA \ cdot (1- \ epsilon) (1+ \ epsilon)}$

Sin embargo, el área total de la elipse es igual a 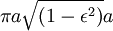$\ Pi a \ sqrt {(1- \ epsilon ^ 2)} un$ . (Eso es lo mismo que 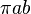$\ Pi a b$ , Porque 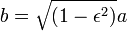$b = \ sqrt {(1- \ epsilon ^ 2)} un$ ). El tiempo que el planeta sacar para barrer toda el área de la elipse es igual área de la elipse, así,

$T \ cdot \ frac {dA} {dt} = \ pi a \ sqrt {(1- \ epsilon ^ 2)} un$

$T \ cdot \ begin {matriz} \ frac {1} {2} \ end {matriz} \ cdot \ sqrt {GMA \ cdot (1- \ epsilon) (1+ \ epsilon)} = \ pi \ sqrt {(1 - \ epsilon ^ 2)} a ^ 2$

$T = \ frac {2 \ pi \ sqrt {(1- \ epsilon ^ 2)} a ^ 2} {\ sqrt {GMA \ cdot (1- \ epsilon) (1+ \ epsilon)}} = \ frac {2 \ pi a ^ 2} {\ sqrt {GMA}} = \ frac {2 \ pi} {\ sqrt {GM}} \ sqrt {a ^ 3}$

$T ^ 2 = \ frac {4 \ pi ^ 2} {GM} a ^ 3.$

Sin embargo, si la masa m no es insignificante en relación con M, entonces el planeta orbita el sol con la misma velocidad y la posición exacta como un cuerpo muy pequeño en órbita un objeto de masa 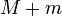$M + m$ (Ver reducción de la masa). Para integrar que en la fórmula anterior, M debe ser reemplazado con 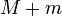$M + m$ , Dar

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} a ^ 3.$

QED

Recuperado de " http://en.wikipedia.org/w/index.php?title=Kepler%27s_laws_of_planetary_motion&oldid=198683410 "

We provide Linux to the World