
Regresión lineal
Acerca de este escuelas selección Wikipedia
SOS Children, una organización benéfica educación , organizó esta selección. Una buena manera de ayudar a otros niños es mediante el patrocinio de un niño
La regresión lineal es una forma de análisis de regresión en el que los datos de observación se modelan por un mínimos cuadrados función que es una combinación lineal de los parámetros del modelo y depende de uno o más variables independientes. En la regresión lineal simple de la función modelo representa una línea recta. Los resultados de los datos ajustados están sujetos a análisis estadístico.
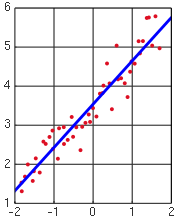
Definiciones
Los datos consisten en valores m 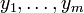 tomado de las observaciones de la variable dependiente ( variable de respuesta)
tomado de las observaciones de la variable dependiente ( variable de respuesta) 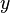 . La variable dependiente está sujeta a error. Se supone que este error sea variable aleatoria , con una media de cero. El error sistemático (por ejemplo, significa ≠ 0) pueden estar presentes, pero su tratamiento está fuera del alcance de los análisis de regresión. La variable independiente ( variable explicativa)
. La variable dependiente está sujeta a error. Se supone que este error sea variable aleatoria , con una media de cero. El error sistemático (por ejemplo, significa ≠ 0) pueden estar presentes, pero su tratamiento está fuera del alcance de los análisis de regresión. La variable independiente ( variable explicativa) 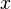 , Es libre de errores. Si esto no es así, el modelado debe hacerse utilizando errores en las variables técnicas de modelo. Las variables independientes son también llamadas regresores, variables exógenas, las variables de entrada y las variables predictoras. En la regresión lineal simple del modelo de datos se escribe como
, Es libre de errores. Si esto no es así, el modelado debe hacerse utilizando errores en las variables técnicas de modelo. Las variables independientes son también llamadas regresores, variables exógenas, las variables de entrada y las variables predictoras. En la regresión lineal simple del modelo de datos se escribe como
donde 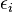 es un error de observación.
es un error de observación. 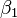 (El origen) y
(El origen) y 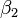 (Pendiente) son los parámetros del modelo. En general, hay parámetros n,
(Pendiente) son los parámetros del modelo. En general, hay parámetros n, 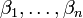 y el modelo se puede escribir como
y el modelo se puede escribir como
donde los coeficientes 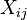 son constantes o funciones de la variable independiente, x. Modelos que no se ajusten a esta especificación deben ser tratadas por regresión no lineal.
son constantes o funciones de la variable independiente, x. Modelos que no se ajusten a esta especificación deben ser tratadas por regresión no lineal.
A menos que se indique lo contrario, se supone que los errores de observación son no correlacionado y pertenecen a una distribución normal . Esto, u otro supuesto, se utiliza cuando se realizan pruebas estadísticas sobre los resultados de la regresión. Una formulación equivalente de regresión lineal simple que muestra explícitamente la regresión lineal como un modelo de expectativa condicional se puede dar como
La distribución condicional de y x dado es una transformación lineal de la distribución del término de error.
Notación y convenciones de nombres
- Los escalares y vectores se denotan por letras minúsculas.
- Las matrices se denotan con letras mayúsculas.
- Los parámetros se denotan con letras griegas.
- Vectores y matrices se denotan por letras en negrita.
- Un parámetro con un sombrero, como
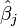 , Se refiere a un estimador de parámetros.
, Se refiere a un estimador de parámetros.
Análisis de mínimos cuadrados
El primer objetivo de análisis de regresión es mejor ajustar los datos mediante el ajuste de los parámetros del modelo. De los diferentes criterios que se pueden utilizar para definir lo que constituye un mejor ajuste, el criterio de mínimos cuadrados es muy poderoso. La función objetivo, S, se define como la suma de los residuos al cuadrado, r i
donde cada residual es la diferencia entre el valor observado y el valor calculado por el modelo:
Se obtiene el mejor ajuste cuando S, la suma de los residuos al cuadrado, se reduce al mínimo. Sujeto a ciertas condiciones, los parámetros a continuación tienen mínimo varianza ( Gauss-Markov teorema) y también puede representar un solución de máxima verosimilitud para el problema de optimización.
De la teoría de la mínimos cuadrados lineales, los estimadores de los parámetros se encuentran resolviendo las ecuaciones normales
En la notación de matrices, estas ecuaciones se escriben como
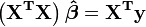 ,
,
Y así, cuando la matriz 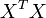 no es singular:
no es singular:
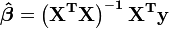 ,
,
Específicamente, para el montaje de línea recta, esto se muestra en apropiado línea recta.
Estadísticas de regresión
El segundo objetivo de la regresión es el análisis estadístico de los resultados de ajuste de datos.
Denotemos por 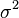 la varianza del término de error
la varianza del término de error  (De modo que
(De modo que 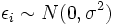 para cada
para cada 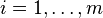 ). Una estimación no sesgada de
). Una estimación no sesgada de 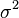 es dado por
es dado por
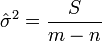 .
.
La relación entre la estimación y el valor verdadero es:
donde 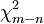 tiene distribución Chi-cuadrado con
tiene distribución Chi-cuadrado con 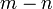 grados de libertad.
grados de libertad.
La aplicación de esta prueba requiere que 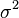 , La varianza de una observación de unidad de peso, ser estimado. Si el
, La varianza de una observación de unidad de peso, ser estimado. Si el 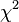 prueba se pasa, los datos se puede decir que ser instalados dentro del error de observación.
prueba se pasa, los datos se puede decir que ser instalados dentro del error de observación.
La solución a las ecuaciones normales se puede escribir como
Esto demuestra que los estimadores de los parámetros son combinaciones lineales de la variable dependiente. De ello se desprende que, si los errores observacionales se distribuyen normalmente, los estimadores de los parámetros pertenecerán a una distribución t de Student con 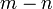 grados de libertad. La desviación estándar en un estimador de parámetros viene dada por
grados de libertad. La desviación estándar en un estimador de parámetros viene dada por
La 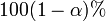 intervalo de confianza para el parámetro,
intervalo de confianza para el parámetro, 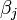 , Se calcula como sigue:
, Se calcula como sigue:
Los residuos se pueden expresar como
La matriz 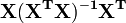 se conoce como el matriz sombrero y tiene la propiedad útil que es idempotente. Usando esta propiedad se puede demostrar que, si los errores se distribuyen normalmente, los residuos seguirán una distribución t de Student con
se conoce como el matriz sombrero y tiene la propiedad útil que es idempotente. Usando esta propiedad se puede demostrar que, si los errores se distribuyen normalmente, los residuos seguirán una distribución t de Student con 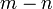 grados de libertad. Residuos studentizados son útiles en las pruebas de valores atípicos.
grados de libertad. Residuos studentizados son útiles en las pruebas de valores atípicos.
Dado un valor de la variable independiente, x d, la respuesta pronosticada se calcula como
Escribir los elementos 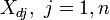 como
como  , La
, La 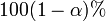 intervalo de confianza de respuesta media de se da la predicción, utilizando la teoría de la propagación de errores, por:
intervalo de confianza de respuesta media de se da la predicción, utilizando la teoría de la propagación de errores, por:
La 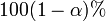 los intervalos de confianza de respuesta predichos para los datos están dados por:
los intervalos de confianza de respuesta predichos para los datos están dados por:
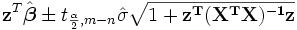 .
.
Caso lineal
En el caso de que la fórmula a ser instalados es una línea recta, 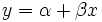 , Las ecuaciones normales son
, Las ecuaciones normales son
donde todas las sumas son desde i = 1 hasta i = m. Desde allí, por La regla de Cramer,
donde
La matriz de covarianza es
La significa intervalo de confianza respuesta está dada por
La intervalo de confianza respuesta predicha está dada por
El análisis de varianza
El análisis de varianza es similar a ANOVA en que la suma de residuos al cuadrado se divide en dos componentes. La suma de cuadrados de regresión (o suma de residuos al cuadrado) SSR (también llamado comúnmente RSS) viene dada por:
donde 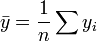 y u es un n por 1 unidad vector (es decir, cada elemento es 1). Tenga en cuenta que los términos
y u es un n por 1 unidad vector (es decir, cada elemento es 1). Tenga en cuenta que los términos 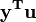 y
y 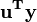 son ambos equivalente a
son ambos equivalente a 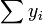 , Y así el término
, Y así el término 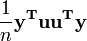 es equivalente a
es equivalente a 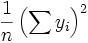 .
.
El error (o inexplicable) suma de los cuadrados ESS está dada por:
La suma total de cuadrados TSS está dada por
El coeficiente de Pearson de regresión, R ² viene dada como
Ejemplo
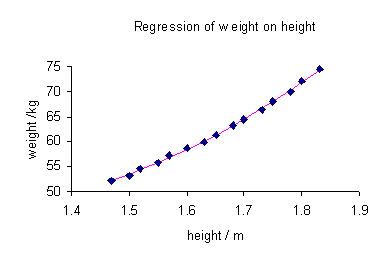
Para ilustrar los diversos objetivos de la regresión, damos un ejemplo. El siguiente conjunto de datos da las alturas y pesos medios de las mujeres estadounidenses mayores de 30-39 (fuente: El Almanaque Mundial y Reserva de Datos de 1975).
Altura / m 1.47 1.5 1.52 1.55 1.57 1.60 1.63 1.65 1.68 1.7 1.73 1.75 1.78 1.8 1.83 Peso (kg 52.21 53.12 54.48 55.84 57.2 58.57 59.93 61.29 63.11 64.47 66.28 68.1 69.92 72.19 74.46
Una parcela de peso en contra de la altura (véase más adelante) muestra que no puede ser modelado por una línea recta, por lo que una regresión se realiza mediante el modelado de los datos por una parábola.
donde la variable dependiente, y, es de peso y la variable independiente, x es la altura.
Coloca los coeficientes, 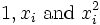 , De los parámetros para la i-ésima observación en el ª fila i de la matriz X.
, De los parámetros para la i-ésima observación en el ª fila i de la matriz X.
Los valores de los parámetros se encuentran resolviendo las ecuaciones normales
Elemento ij de la matriz normal de la ecuación, 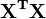 está formada por la suma de los productos de la columna i y la columna j de X.
está formada por la suma de los productos de la columna i y la columna j de X.
Elemento i del vector lado derecho 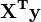 está formada por la suma de los productos de la columna i de X con la columna de valores de variables independientes.
está formada por la suma de los productos de la columna i de X con la columna de valores de variables independientes.
Por lo tanto, las ecuaciones normales son
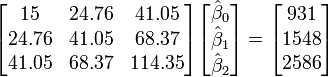
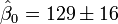 (Valor
(Valor 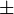 desviacion estandar)
desviacion estandar) 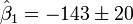
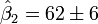
Los valores calculados se dan por
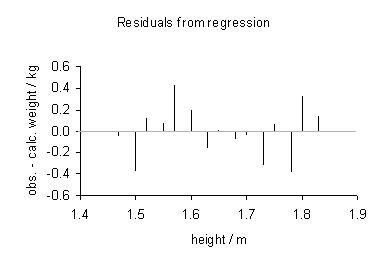
Los datos observados y calculados se representan juntos y los residuos, 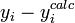 , Se calculan y se representan. Las desviaciones estándar se calculan mediante la suma de los cuadrados,
, Se calculan y se representan. Las desviaciones estándar se calculan mediante la suma de los cuadrados, 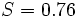 .
.
Los intervalos de confianza se calculan usando:
con 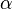 = 5%,
= 5%, 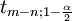 = 2,2. Por lo tanto, podemos decir que el 95% los intervalos de confianza son:
= 2,2. Por lo tanto, podemos decir que el 95% los intervalos de confianza son:
Comprobación de las hipótesis del modelo
Los supuestos del modelo se comprueban mediante el cálculo de los residuos y trazarlos. Los siguientes gráficos se pueden construir para probar la validez de los supuestos:
- Los residuos según la variable, como se ilustra arriba.
- La serie gráfico de tiempo de los residuos, es decir, el trazado de los residuales como una función del tiempo.
- Residuos contra los valores ajustados,
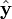 .
. - Residuos contra el residual anterior.
- Un gráfico de probabilidad normal de los residuales para probar la normalidad. Los puntos deben estar en línea recta.
No debe haber ningún patrón perceptible a los datos en todo menos en la última trama
Comprobación de la validez del modelo
La validez del modelo se puede comprobar con cualquiera de los métodos siguientes:
- Usando el intervalo de confianza para cada uno de los parámetros,
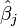 . Si el intervalo de confianza incluye 0, entonces el parámetro puede ser retirado del modelo. Idealmente, sería necesario un nuevo análisis de regresión excluyendo ese parámetro a realizar y continuó hasta que no hay más parámetros para eliminar.
. Si el intervalo de confianza incluye 0, entonces el parámetro puede ser retirado del modelo. Idealmente, sería necesario un nuevo análisis de regresión excluyendo ese parámetro a realizar y continuó hasta que no hay más parámetros para eliminar. - En el montaje de una línea recta, calcular el coeficiente de Pearson de regresión. Cuanto más cerca el valor es 1; mejor es la regresión es. Este coeficiente da qué fracción de la conducta observada se explica por las variables dadas.
- El examen de los intervalos de confianza de observación y predicción. Cuanto más pequeños son los mejores.
- Cálculo de la F-estadísticas.
Otros procedimientos
Mínimos cuadrados ponderados
Mínimos cuadrados ponderados es una generalización del método de mínimos cuadrados, que se utiliza cuando los errores observacionales tienen varianza desigual.
Errores en las variables del modelo
Errores en las variables de modelo o total de los mínimos cuadrados cuando la variable independiente está sujeta a error
Modelo lineal generalizado
Modelo lineal generalizado se utiliza cuando la función de distribución de los errores no es una distribución Normal. Los ejemplos incluyen la distribución exponencial , distribución gamma, Distribución Inversa de Gauss, la distribución de Poisson , distribución binomial , distribución multinomial
Regresión robusta
Una serie de enfoques alternativos para el cálculo de los parámetros de regresión se incluyen en la categoría conocida como regresión robusta. Una técnica minimiza la media error absoluto, o alguna otra función de los residuos, en lugar de error cuadrático medio como en la regresión lineal. Regresión robusta es mucho más computacionalmente intensivas que la regresión lineal y es algo más difícil de implementar también. Mientras menos estimaciones plazas no son muy sensibles a la ruptura de la normalidad de la suposición de errores, esto no es cierto cuando la varianza o media de la distribución de error no está acotado, o cuando un analista que puede identificar valores atípicos no está disponible.
Entre Usuarios de Stata, regresión robusta se toma con frecuencia en el sentido de regresión lineal con las estimaciones de error estándar Huber-blancos debido a las convenciones de nomenclatura para los comandos de regresión. Este procedimiento se relaja el supuesto de homocedasticidad de varianza estima solamente; los predictores son todavía mínimos cuadrados ordinarios (MCO) estimaciones. Esta vez en cuando lleva a la confusión; Usuarios de Stata veces creen que la regresión lineal es un método robusto cuando se utiliza esta opción, aunque en realidad no es robusto en el sentido de outlier-resistencia.
Aplicaciones de la regresión lineal
La regresión lineal es ampliamente utilizado en las ciencias biológicas, conductuales y sociales para describir las relaciones entre las variables. Esta considerado como una de las herramientas más importantes que se utilizan en estas disciplinas.
La línea de tendencia
Una línea de tendencia representa un tendencia, el movimiento a largo plazo en datos de series de tiempo después de otros componentes han tenido en cuenta. Le dice si un conjunto de datos en particular (digamos PIB, los precios del petróleo o precios de las acciones) han aumentado o disminuido durante el período de tiempo. Una línea de tendencia podría simplemente ser dibujado por ojo a través de un conjunto de puntos de datos, pero más adecuadamente su posición y la pendiente se calcula utilizando técnicas estadísticas como la regresión lineal. Las líneas de tendencia típicamente son líneas rectas, aunque algunas variaciones utilizan polinomios de grado superior, dependiendo del grado de curvatura deseada en la línea.
Las líneas de tendencia se utilizan a veces en Business Analytics para mostrar los cambios en los datos a través del tiempo. Esto tiene la ventaja de ser simple. Las líneas de tendencia se utilizan a menudo para argumentar que una acción particular o evento (como la formación, o una campaña publicitaria) causaron los cambios observados en un punto en el tiempo. Esta es una técnica simple, y no requiere de un grupo de control, el diseño experimental, o una técnica de análisis sofisticado. Sin embargo, adolece de una falta de validez científica en los casos en que otros cambios potenciales pueden afectar a los datos.
Medicina
Como un ejemplo, la evidencia preliminar en relación fumar tabaco a la mortalidad y la morbilidad vino de estudios que emplean regresión. Los investigadores por lo general incluyen varias variables en su análisis de regresión en un esfuerzo por eliminar los factores que podrían producir correlaciones espurias. Para el ejemplo tabaquismo, los investigadores podrían incluir el estatus socio-económico, además de fumar para asegurar que cualquier efecto del tabaquismo sobre la mortalidad observada no se debe a un efecto de la educación o ingresos. Sin embargo, nunca es posible incluir todas las posibles variables de confusión en un estudio de regresión empleando. Para el ejemplo de fumar, un hipotético gen podría aumentar la mortalidad y también hacer que las personas fuman más. Por esta razón, Los ensayos controlados aleatorios se consideran más fiables que un análisis de regresión.
Finanzas
La Capital Asset Pricing Model utiliza la regresión lineal, así como el concepto de Beta para analizar y cuantificar el riesgo sistemático de una inversión. Esto viene directamente de la Coeficiente Beta del modelo de regresión lineal que relaciona el rendimiento de la inversión para el retorno de todos los activos de riesgo.
Regresión puede no ser la forma apropiada para estimar beta en finanzas, dado que se supone que debe proporcionar la volatilidad de una inversión con respecto a la volatilidad del mercado en su conjunto. Para ello sería necesario que tanto estas variables ser tratados de la misma manera cuando se estima la pendiente. Mientras trata de regresión toda la variabilidad como en la inversión vuelve variable, es decir que sólo tiene en cuenta los residuos en la variable dependiente.

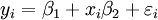
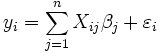
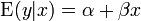
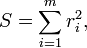
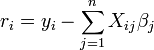
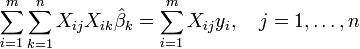
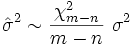
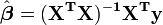
![\ Sombrero \ sigma_j = \ sqrt {\ frac {S} {mn} \ left [\ mathbf {(X ^ TX)} ^ {- 1} \ right] _ {jj}}](../../images/216/21697.png)
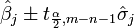
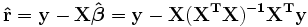
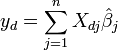
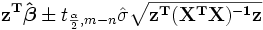
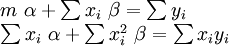
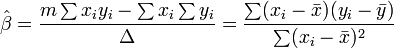
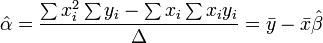
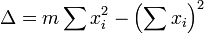
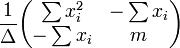
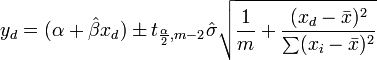
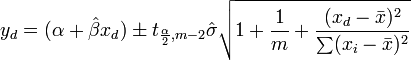
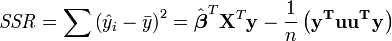
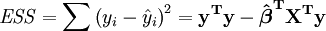
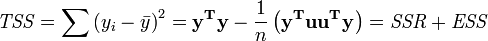
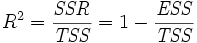
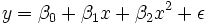
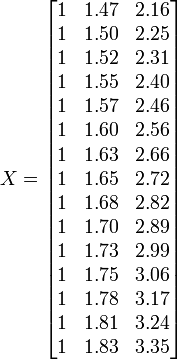
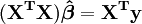
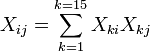
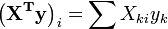
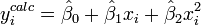
![[\ Hat {\ beta_j} - \ sigma_j t_ {mn; 1- \ frac {\ alpha} {2}}; \ hat {\ beta_j} + \ sigma_j t_ {mn; 1- \ frac {\ alpha} {2 }}]](../../images/217/21747.png)
![\ Beta_0 \ in [92.9,164.7]](../../images/217/21749.png)
![\ Beta_1 \ in [-186,8, -99,5]](../../images/217/21750.png)
![\ Beta_2 \ in [48.7,75.2]](../../images/217/21751.png)
