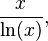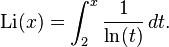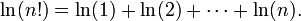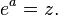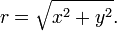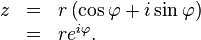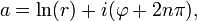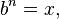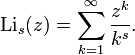Logaritmo
Acerca de este escuelas selección Wikipedia
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Madres SOS cada aspecto después de un una familia de niños apadrinados .
El logaritmo de un número es el exponente por las que otro valor fijo, la base, debe ser elevada para producir ese número. Por ejemplo, el logaritmo de 1000 a la base 10 es 3, porque 1000 es 10 a la potencia 3:. 1000 = 10 × 10 × 10 = 10 3 Más generalmente, si x = b y, entonces y es el logaritmo de x para base b, y se escribe y = log b (x), de modo de registro 10 (1000) = 3.
El logaritmo en base b = 10 se llama la logaritmo común y tiene muchas aplicaciones en la ciencia y la ingeniería. El logaritmo natural tiene la constante e (≈ 2.718) como su base; su uso está muy extendido en matemáticas puras, especialmente cálculo . La logaritmo binario utiliza la base b = 2 y es prominente en ciencias de la computación .
Los logaritmos fueron introducidos por John Napier en el siglo 17 como un medio para simplificar los cálculos. Ellos fueron adoptados rápidamente por los navegantes, científicos, ingenieros, y otros para realizar cálculos con mayor facilidad, utilizando reglas de cálculo y tablas de logaritmos. Pasos de multiplicación de varios dígitos tediosas pueden sustituirse por tabla de subidas y sencillo además por el hecho - importante por derecho propio - que el logaritmo de un producto es el suma de los logaritmos de los factores:
La noción actual de logaritmos viene de Leonhard Euler , que los conecta a la función exponencial en el siglo 18.
Las escalas logarítmicas reducen las cantidades de amplio alcance a ámbitos más pequeños. Por ejemplo, el decibel es una unidad de cuantificación logarítmica relaciones de presión y tensión de sonido. En química, El pH es una medida logarítmica para la acidez de una solución acuosa. Los logaritmos son comunes en científicos fórmulas , y en las medidas de la la complejidad de los algoritmos y de objetos geométricos llama fractales . Describen intervalos musicales, aparecen en las fórmulas contando números primos , informan algunos modelos en psicofísica, y pueden ayudar a contabilidad forense.
De la misma manera como el logaritmo invierte la exponenciación , la logaritmo complejo es la función inversa de la función exponencial se aplica a los números complejos . La logaritmo discreto es otra variante; Tiene aplicaciones en criptografía de clave pública.
Motivación y definición
La idea de los logaritmos es invertir la operación de exponenciación , que está levantando un número a una potencia. Por ejemplo, la tercera potencia (o cubo) de 2 es 8, 8 porque es el producto de tres factores de 2:
De ello se deduce que el logaritmo de 8 con respecto a la base 2 es 3, por lo que log 2 8 = 3.
Exponenciación
La tercera potencia de un número b es el producto de tres factores de b. Más en general, elevando b a la potencia n-ésima, donde n es un número natural , se hace multiplicando n factores de b. La potencia n-ésima de b se escribe b n, por lo que
Exponentation puede extenderse a b y, donde b es un número positivo y el exponente y es cualquier número real . Por ejemplo, b -1 es la recíproco de b, es decir, 1 / b.
Definición
El logaritmo de un número x con respecto a la base b es el exponente b por el cual debe ser elevada para producir x. En otras palabras, el logaritmo de x a la base b es la solución y a la ecuación
El logaritmo se denota "log b (x)" (pronunciado como "el logaritmo de x en base b" o "la b logaritmo valor inicial de x"). En la ecuación y = log b (x), el valor de y es la respuesta a la pregunta "¿Para qué poder tiene las b elevarse, con el fin de producir x?". Para definir el logaritmo, la base b debe ser una número real positivo no es igual a 1 y x debe ser un número positivo.
Ejemplos
Por ejemplo, log 2 (16) = 4, desde el 2 de 4 = 2 x 2 x 2 x 2 = 16. Los logaritmos también pueden ser negativos:
desde
Un tercer ejemplo:. Log 10 (150) es de aproximadamente 2.176, que se encuentra entre 2 y 3, así como 150 se encuentra entre 10 y 100 = 2 10 3 = 1000 Por último, para cualquier base b, log b (b) = 1 y log b (1) = 0, ya que b = 1 y b = 0 b 1, respectivamente.
Identidades logarítmicas
Varias fórmulas importantes, a veces se llaman identidades logarítmicas o registro leyes, se relacionan entre sí los logaritmos.
Producto, cociente, potencia y raíz
El logaritmo de un producto es la suma de los logaritmos de los números que se multiplican; el logaritmo de la relación de dos números es la diferencia de los logaritmos. El logaritmo de la potencia de p-ésima de un número es p veces el logaritmo de la propia serie; el logaritmo de una raíz p-ésimo es el logaritmo del número dividido por p. La siguiente tabla muestra estas identidades con ejemplos:
| Fórmula | Ejemplo | |
|---|---|---|
| producto | 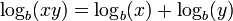 | 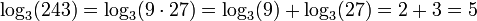 |
| cociente | 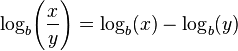 | 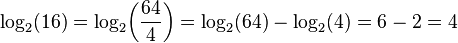 |
| energía | 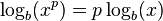 | 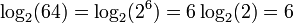 |
| raíz | ![\ Log_b \ sqrt [p] {x} = \ frac {\ log_b (x)} p \,](../../images/2455/245579.png) | 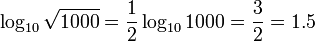 |
Cambio de la base
El registro de logaritmo b (x) se puede calcular a partir de los logaritmos de x y b con respecto a una base arbitraria k utilizando la siguiente fórmula:
Típico calculadoras científicas calcular los logaritmos a las bases 10 y e. Los logaritmos con respecto a cualquier base b se pueden determinar usando cualquiera de estas dos logaritmos por la fórmula anterior:
Dado un número x y su logaritmo log b (x) a una base desconocida b, la base está dada por:
Bases particulares
Entre todas las opciones para la base b, tres son particularmente comunes. Estos son b = 10, b = e (la irracional constante matemática ≈ 2,71828), y b = 2. En el análisis matemático , el logaritmo en base e es generalizada debido a sus propiedades de análisis particulares se explica a continuación. Por otro lado, de bases 10 logaritmos son fáciles de usar para los cálculos manuales en el decimal sistema de numeración:
Por lo tanto, log 10 (x) está relacionada con el número de dígitos decimales de un número entero positivo x: el número de dígitos es el más pequeño número entero estrictamente mayor que log 10 (x). Por ejemplo, log 10 (1430) es de aproximadamente 3,15. El siguiente entero es de 4, que es el número de dígitos de 1430. El logaritmo en base dos se utiliza en la informática , en el que el sistema binario es ubicuo.
La siguiente tabla muestra las notaciones comunes de logaritmos a estas bases y los campos en los que se utilizan. Muchas disciplinas escriben log (x) en lugar de log b (x), cuando la base prevista se puede determinar a partir del contexto. El registro de la notación b (x) también ocurre. Los "ISO notación" listas de columna designaciones propuestas por el Organización Internacional de Normalización ( ISO 31-11).
| Base b | Nombre de registro b (x) | Notación ISO | Otras notaciones | Utilizado en |
|---|---|---|---|---|
| 2 | logaritmo binario | libras (x) | ld (x), log (x), lg (x) | ciencias de la computación, teoría de la información, las matemáticas |
| e | logaritmo natural | ln (x) | log (x) (En matemáticas y en muchos lenguajes de programación ) | análisis matemático, física, química, estadísticas , economía y algunos campos de la ingeniería |
| 10 | logaritmo común | lg (x) | log (x) (En la ingeniería, la biología, la astronomía), | varios de ingeniería campos (véase decibelios y ver más adelante), logaritmo tablas, de mano calculadoras, espectroscopia |
Historia
Antecesores
La Babilonios en algún momento en 2000-1600 antes de Cristo pudo haber inventado el trimestre cuadrado algoritmo de multiplicación para multiplicar dos números usando sólo la suma, resta y una tabla de cuadrados. Sin embargo, no se podría utilizar para la división sin una tabla adicional de los recíprocos. Las grandes tablas de cuadrados trimestre se utilizan para simplificar la multiplicación precisa de un gran número de 1817 en adelante hasta que este fue reemplazado por el uso de las computadoras.
Michael Stifel publicó Arithmetica integra en Nuremberg en 1544, que contiene una tabla de números enteros y potencias de 2 que se ha considerado una primera versión de una tabla de logaritmos.
En los siglos 16 y principios del 17o un algoritmo llamado Prostaféresis se utiliza para aproximar la multiplicación y la división. Este utiliza la identidad trigonométrica
o similar para convertir las multiplicaciones de adiciones y búsquedas de la tabla. Sin embargo logaritmos son más directas y requieren menos trabajo. Se puede demostrar el uso de números complejos que esto es básicamente la misma técnica.
De Napier a Euler

El método de los logaritmos fue propuesto públicamente por John Napier en 1614, en un libro titulado Mirifici Logarithmorum Canonis Descriptio (Descripción del maravilloso Estado de logaritmos). Joost Bürgi inventó independientemente logaritmos pero publica seis años después de Napier.
Johannes Kepler , quien utilizó tablas de logaritmos extensivamente para compilar su Efemérides y por lo tanto lo dedicó a Napier, comentó:
... El acento en el cálculo llevó Justus Byrgius [Joost Bürgi] en el camino a estos años muy logaritmos muchos antes que el sistema de Napier apareció; pero ... en vez de criar a su hijo para el beneficio público desertó en el nacimiento.-Johannes Kepler, Tablas Rudolfinas (1627)
Por sustracciones repetidas Napier calcula (1 - 10 -7) L para L que van desde 1 a 100. El resultado para L = 100 es de aproximadamente 0,99999 = 1 - 10 -5. Napier continuación, calcula los productos de estos números con 10 7 (1 - 10 -5) para L L de 1 a 50, y lo hizo de manera similar con 0.9998 ≈ (1 - 10 -5) 20 y 0,9 ≈ 0,995 20. Estos cálculos, que ocuparon 20 años, le permitieron dar, para cualquier número N 5-10 millones, el número L que resuelve la ecuación
Napier primera llamada L un "número artificial", pero más tarde se introdujo la palabra "logaritmo" para referirse a un número que indica una relación: λόγος ( logos) que significa la proporción y ἀριθμός (arithmos), que significa número. En notación moderna, la relación con los logaritmos naturales es:
donde el aproximación muy cercana corresponde a la observación de que
La invención fue rápida y ampliamente se reunió con la aclamación. Las obras de Bonaventura Cavalieri (Italia), Edmund Wingate (Francia), Xue Fengzuo (China), y Johannes Kepler 's Chilias logarithmorum (Alemania) contribuyeron a difundir el concepto.
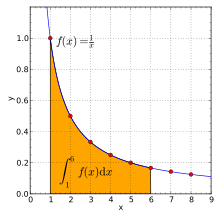
En 1647 Grégoire de Saint-Vincent logaritmos relacionado con la cuadratura de la hipérbola, señalando que el área de f (t) bajo la hipérbola desde x = 1 hasta x = t satisface
El logaritmo natural fue descrita por primera vez por Nicholas Mercator en su obra Logarithmotechnia publicado en 1668, aunque las matemáticas profesor John Speidell ya tenía en 1619 compiló una tabla en el logaritmo natural. Alrededor de 1730, Leonhard Euler definió la función exponencial y el logaritmo natural
Euler también mostró que las dos funciones son inversas entre sí.
Tablas de logaritmos, reglas de cálculo y aplicaciones históricas

Al simplificar los cálculos difíciles, logaritmos contribuyeron al avance de la ciencia, y en especial de la astronomía . Ellos fueron críticos a los avances en topografía, navegación astronómica, y otros dominios. Pierre-Simon Laplace llamados logaritmos
- "... [A] n artificio admirable que, al reducir a unos pocos días el trabajo de muchos meses, duplica la vida del astrónomo, y le perdona los errores y disgusto inseparables de cálculos largos."
Una herramienta clave que permitió el uso práctico de los logaritmos antes de calculadoras y computadoras era la tabla de logaritmos. El primero de estos tabla fue compilada por Henry Briggs en 1617, inmediatamente después de la invención de Napier. Posteriormente, las tablas con el aumento de alcance y precisión fueron escritos. Estas tablas enumeran los valores de log b (x) y b x para cualquier número x en un cierto rango, a una cierta precisión, para una cierta base b (generalmente b = 10). Por ejemplo, la primera mesa de Briggs contenía los logaritmos comunes de todos los números enteros en el rango de 1 a 1000, con una precisión de 8 dígitos. A medida que la función f (x) = b x es la función inversa de log b (x), se le ha llamado el antilogaritmo. El producto y el cociente de dos números c y d positivos se calcularon de forma rutinaria como la suma y la diferencia de sus logaritmos. El CD del producto o cociente c / d vino de buscar el antilogaritmo de la suma o la diferencia, también a través de la misma mesa:
y
Para los cálculos manuales que exigen precisión apreciable, la realización de las operaciones de búsqueda de los dos logaritmos, que calculen su suma o diferencia, y buscar el antilogaritmo es mucho más rápido que realizar la multiplicación por métodos anteriores, como Prostaféresis, que se basa en identidades trigonométricas. Los cálculos de los poderes y raíces se reducen a multiplicaciones o divisiones y las operaciones de búsqueda por
y
Muchas tablas de logaritmos dan logaritmos proporcionando separado la característica y mantisa de x, es decir, la parte entera y la parte fraccionaria de log 10 (x). La característica de 10 · x es uno más la característica de x, y su significandos son los mismos. Esto amplía el ámbito de tablas de logaritmos: dado un registro de la tabla 10 lista (x) para todos los enteros x van de 1 a 1000, el logaritmo de 3542 se aproxima por
Otra aplicación crítica fue el regla de cálculo, un par de escalas logarítmica divididos utilizados para el cálculo, como se ilustra aquí:
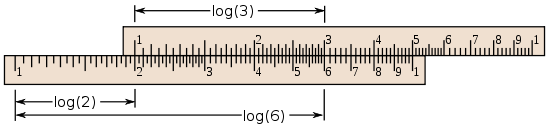
La escala logarítmica no deslizante, La regla de Gunter, se inventó poco después de la invención de Napier. William Oughtred mejorado para crear la diapositiva regla un par de escalas logarítmicas móvil con respecto a la otra. Los números se colocan en escalas correderas a distancias proporcionales a las diferencias entre sus logaritmos. Deslizar la escala superior asciende adecuadamente a añadir mecánicamente logaritmos. Por ejemplo, la adición de la distancia de 1 a 2 de la escala inferior a la distancia de 1 a 3 en la escala superior produce un producto de 6, que se lee en la parte inferior. La regla de cálculo es una herramienta esencial para el cálculo de los ingenieros y los científicos hasta la década de 1970, ya que permite, a expensas de la precisión, la computación mucho más rápido que las técnicas basadas en tablas.
Propiedades analíticas
Un estudio más profundo de los logaritmos requiere el concepto de una función . Una función es una regla que, dado un número, produce otro número. Un ejemplo es la función de producir el x-ésimo poder de b a partir de cualquier número real x, donde la base b es un número fijo. Esta función se escribe
Función logarítmica
Para justificar la definición de logaritmos, es necesario demostrar que la ecuación
tiene una solución x, y que esta solución es única, a condición de que y es positiva y que b es positivo y desigual a 1. Las pruebas de este hecho requiere la teorema del valor intermedio de la primaria cálculo . Este teorema establece que un función continua que produce dos valores m y n también produce cualquier valor que se encuentra entre m y n. Una función es continua si no lo hace "saltar", es decir, si su gráfica se puede dibujar sin levantar el lápiz.
Esta propiedad se puede demostrar que mantener durante la función f (x) = b x. Debido f toma arbitrariamente grandes y arbitrariamente pequeños valores positivos, cualquier número y> 0 se encuentra entre f (x 0) y f (x 1) para la adecuada x 0 y x 1. Por lo tanto, el teorema del valor intermedio se garantiza que la ecuación f (x) = y tiene una solución. Además, sólo hay una solución a esta ecuación, ya que la función f es estrictamente creciente (para b 1>), o estrictamente decreciente (para 0 <b <1).
La solución única x es el logaritmo de y para la base b, b (y) de registro. La función que asigna a y su logaritmo se llama función logarítmica o función logarítmica (o simplemente logaritmo).
Función inversa
La fórmula para el logaritmo de una potencia dice en particular, que para cualquier número x,
En prosa, tomando el x-ésima potencia de b y luego el b logaritmo basal devuelve x. Por el contrario, dado un número y positivo, la fórmula
dice que la toma primero el logaritmo y luego exponentiating devuelve y. Así, las dos formas posibles de combinar (o componer ) logaritmos y exponentes devuelven el número original. Por lo tanto, el logaritmo en base b es la función inversa de f (x) = b x.
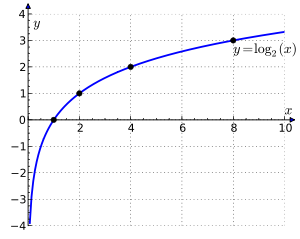
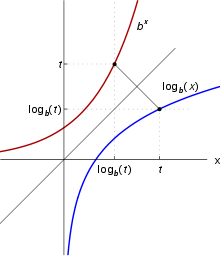
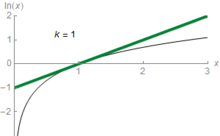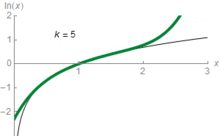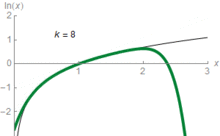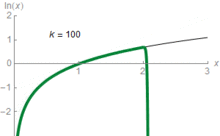
Funciones inversas están estrechamente relacionados con las funciones originales. Su gráficos se corresponden entre sí en sus intercambios de la x - y las coordenadas x Y (o después de reflexionar en la diagonal recta x = y), como se muestra a la derecha: un punto (t, u = b t) en el gráfico de rendimiento f un punto (u, t = log b u) en el gráfico del logaritmo y viceversa. Como consecuencia, b (x) log diverge a infinito (se hace más grande que cualquier número dado) si x crece hasta el infinito, a condición de que b es mayor que uno. En ese caso, b (x) log es un función creciente. Para b <1, log b (x) tiende a menos infinito en su lugar. Cuando x se aproxima a cero, log b (x) va a menos infinito para b> 1 (más infinito para b <1, respectivamente).
Derivada y antiderivada
Propiedades analíticas de las funciones pasan a sus inversas. Así, como f (x) = b x es un continuo y función diferenciable, por lo que es log b (y). Aproximadamente, una función continua es diferenciable si su gráfica no tiene "esquinas" afilados. Además, como el derivado de f (x) se evalúa como ln (b) b x por las propiedades de la función exponencial , la regla de la cadena implica que la derivada de log b (x) viene dada por
Es decir, el pendiente de la tangente que toca la gráfica de la basal b logaritmo en el punto (x, log b (x)) es igual a 1 / (x ln (b)). En particular, la derivada de ln (x) es 1 / x, que implica que la primitiva de 1 / x es ln (x) + C. El derivado con un argumento funcional generalizado f (x) es
El cociente en el lado de la mano derecha se llama la derivada logarítmica de f. Cálculo de f '(x) por medio de la derivada de ln (f (x)) es conocido como diferenciación logarítmica. La antiderivada del logaritmo natural ln (x) es:
Fórmulas relacionadas, tales como primitivas de los logaritmos a otras bases se pueden derivar de esta ecuación usando el cambio de bases.
Representación integral del logaritmo natural
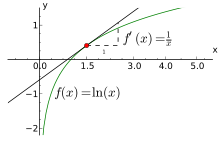
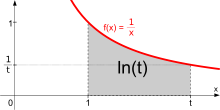
El logaritmo natural de la t de acuerdo con la integral de 1 / x dx de 1 a t:
En otras palabras, ln (t) es igual a la zona entre el eje X y la gráfica de la función 1 / x, que van desde x = 1 para x = t (figura de la derecha). Esto es una consecuencia de la teorema fundamental del cálculo y el hecho de que derivado de ln (x) es 1 / x. El lado derecho de esta ecuación puede servir como una definición del logaritmo natural. Fórmulas de los productos y de logaritmos de potencia se pueden derivar de esta definición. Por ejemplo, la fórmula del producto ln (tu) = ln (t) + ln (u) se deduce como:
La igualdad (1) divide la integral en dos partes, mientras que la igualdad (2) es un cambio de variable (w = x / t). En la siguiente ilustración, la división corresponde a la división en las partes amarillas y azules. Reescalando el área azul mano izquierda verticalmente por el factor de t y la contracción por el mismo factor horizontal no cambia su tamaño. Mover adecuadamente, el área se ajusta a la gráfica de la función f (x) = 1 / x de nuevo. Por lo tanto, el área azul mano izquierda, que es la integral de f (x) de T a tu es la misma que la integral de 1 a u. Esto justifica la igualdad (2) con una prueba más geométrica.
La fórmula de potencia ln (t r) = r ln (t) se puede derivar de una manera similar:
La segunda igualdad utiliza un cambio de variables ( la integración por sustitución), w = x 1 / r.
La suma sobre los recíprocos de los números naturales,
se llama serie armónica. Está íntimamente ligada al logaritmo natural: cuando n tiende a infinito , la diferencia,
converge (es decir, se pone arbitrariamente cerca) a un número conocido como Constante de Euler-Mascheroni. Esto ayuda en el análisis de la relación rendimiento de los algoritmos tales como quicksort.
Hay también otra representación integral del logaritmo que es útil en algunas situaciones.
Esto puede ser verificada mediante demostrando que tiene el mismo valor en x = 1, y el mismo derivado.
Trascendencia del logaritmo
El logaritmo es un ejemplo de una función trascendental y desde un punto de vista teórico, la Gelfond-Schneider teorema afirma que los logaritmos suelen tener valores "difíciles". La declaración formal se basa en la noción de números algebraicos, que incluye todos los números racionales , sino también los números como el raíz cuadrada de 2 o
Los números complejos que no son algebraicos se llaman trascendental; por ejemplo, π y e son esos números. Casi todos los números complejos son trascendentales. El uso de estas nociones, las teorema de Gelfond-Scheider que dan dos números algebraicos ayb, log b (a) es un número trascendental o un número racional p / q (en cuyo caso q = b p, por lo que a y b estaban estrechamente relacionados, para empezar).
Cálculo
Los logaritmos son fáciles de calcular, en algunos casos, tales como log 10 (1000) = 3. En general, los logaritmos pueden calcularse utilizando series de potencias o la -aritmética media geométrica, o recuperar de una precalculada logaritmo tabla que proporciona una precisión fija. el método de Newton , un método iterativo para resolver ecuaciones aproximadamente, también se puede utilizar para calcular el logaritmo, porque su función inversa, la función exponencial, se puede calcular de manera eficiente. El uso de tablas de consulta, CORDIC métodos similares se pueden utilizar para calcular logaritmos si las únicas operaciones disponibles son la suma y la desplazamientos de bit. Además, el logaritmo binario algoritmo calcula libras (x) recursivamente basado en squarings repetidas de x, tomando ventaja de la relación
Series de potencias
- Serie de Taylor
Para cualquier número real z que satisface 0 <z <2, la siguiente fórmula sostiene:
Esta es una forma abreviada de decir que ln (z) se puede aproximar a un valor mucho más precisas por las siguientes expresiones:
Por ejemplo, con z = 1,5 la tercera aproximación produce 0,4167, que es aproximadamente 0,011 mayor que ln (1,5) = 0,405465. Este serie se aproxima a ln (z) con precisión arbitraria, siempre que el número de sumandos es lo suficientemente grande. En el cálculo elemental, ln (z), por lo tanto es el límite de esta serie. Es la serie de Taylor del logaritmo natural en z = 1 La serie de Taylor de ln z proporciona una aproximación particularmente útil para ln (1 + z) cuando z es pequeña, |. z | << 1, desde entonces
Por ejemplo, con z = 0,1 a la aproximación de primer orden da ln (1,1) ≈ 0,1, que es menor que 5% en el valor correcto 0,0953.
- Serie más eficiente
Otra serie se basa en la área función tangente hiperbólica:
para cualquier número real z> 0. Utilizando el Notación Sigma, esto también se escribe como
Esta serie se puede derivar de la serie de Taylor anteriormente. Se converge más rápidamente que la serie de Taylor, especialmente si z es cercana a 1. Por ejemplo, para z = 1.5, los tres primeros términos de la ln aproximada segunda serie (1.5) con un error de aproximadamente 3 × 10 -6. La convergencia rápida para z cercano a 1 se puede tomar ventaja de la siguiente manera: dado un ln baja precisión aproximación y ≈ (z) y poniendo
el logaritmo de z es:
Cuanto mejor es la aproximación inicial y es, más cerca A es a 1, por lo que su logaritmo se puede calcular de manera eficiente. Una puede ser calculada usando la serie exponencial , que converge siempre rápidamente y no es demasiado grande. Cálculo del logaritmo de z más grande se puede reducir a valores más pequeños de z escribiendo z = a · 10 b, de modo que ln (z) = ln (a) + b · ln (10).
Un método estrechamente relacionado se puede utilizar para calcular el logaritmo de números enteros. De la serie anterior, se deduce que:
Si se conoce el logaritmo de un gran número entero n, entonces esta serie produce una serie convergente rápido para log (n +1).
Aproximación media aritmética-geométrica
La -aritméticas geométrica rendimientos medios aproximaciones de alta precisión del logaritmo natural. ln (x) se aproxima a una precisión de 2 - p (o p bits precisos) por la siguiente fórmula (debido a Carl Friedrich Gauss ):
Aquí M denota la media aritmética geométrica. Se obtiene calculando repetidamente la media ( media aritmética ) y la raíz cuadrada del producto de dos números ( media geométrica). Por otra parte, m se elige de tal manera que
Tanto la media aritmética geométrica y las constantes π y ln (2) se puede calcular con la convergencia de la serie rápidamente.
Aplicaciones
Los logaritmos tienen muchas aplicaciones dentro y fuera de las matemáticas. Algunos de estos hechos están relacionados con la noción de invariancia de escala. Por ejemplo, cada cámara de la cáscara de un Nautilus es una copia aproximada de la siguiente, a escala por un factor constante. Esto da lugar a una espiral logarítmica. La ley de Benford en la distribución de dígitos iniciales también se puede explicar por la invariancia de escala. Los logaritmos también están vinculados a auto-similitud. Por ejemplo, los logaritmos aparecen en el análisis de algoritmos que resuelven un problema dividiéndolo en dos pequeños problemas similares y remendar sus soluciones. Las dimensiones de las formas geométricas auto-similares, es decir, formas cuyas partes parecerse a la imagen general se basan también en logaritmos. Las escalas logarítmicas son útiles para cuantificar el cambio relativo de un valor en oposición a su diferencia absoluta. Por otra parte, debido a que la función logarítmica log (x) crece muy lentamente para grandes x, escalas logarítmicas se utilizan para comprimir datos científicos a gran escala. Los logaritmos también se producen en numerosas fórmulas científicas, tales como la Ecuación del cohete Tsiolkovsky, el Ecuación de Fenske, o la Ecuación de Nernst.
Escala logarítmica
Cantidades científicos a menudo se expresan como logaritmos de otras magnitudes, utilizando una escala logarítmica. Por ejemplo, el decibelio es una unidad logarítmica de medición. Se basa en el logaritmo común de Razones - 10 veces el logaritmo común de un relación de potencia o 20 veces el logaritmo común de una relación de voltaje. Se utiliza para cuantificar la pérdida de los niveles de tensión en la transmisión de señales eléctricas, para describir los niveles de potencia de los sonidos en acústica, y la absorbancia de la luz en los campos de la espectrometría y la óptica . La la relación señal a ruido describe la cantidad de subproductos no deseados ruido en relación con un (significativa) señal también se mide en decibelios. En la misma línea, la PSNR es comúnmente utilizado para evaluar la calidad del sonido y métodos de compresión de imagen utilizando el logaritmo.
La fuerza de un terremoto se mide tomando el logaritmo común de la energía emitida por el sismo. Esto se utiliza en la momento en escala de magnitud o la Escala de Richter. Por ejemplo, un terremoto de 5,0 libera 10 veces y un 6,0 libera 100 veces la energía de un 4,0. Otra escala logarítmica es magnitud aparente. Mide el brillo de las estrellas de forma logarítmica. Sin embargo, otro ejemplo es pH en la química ; pH es el negativo del logaritmo común de la la actividad de iones hidronio (la forma de hidrógeno iones H + toman en agua). La actividad de los iones hidronio en agua neutra es 10 -7 mol·L -1, por lo tanto, un pH de 7. El vinagre tiene típicamente un pH de aproximadamente 3. La diferencia de 4 corresponde a una relación de 10 4 de la actividad, es decir, la actividad del ion hidronio de vinagre es de aproximadamente 10 -3 mol · L -1.
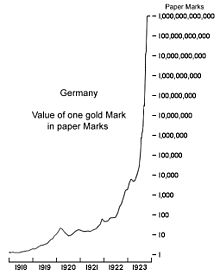
Gráficos semilogarítmico (log-lineales) utilizan el concepto de escala logarítmica para la visualización: un eje, normalmente el vertical, se escala logarítmica. Por ejemplo, el gráfico de la derecha comprime el fuerte aumento 1.000.000-1000000000000 al mismo espacio (en el eje vertical) como el aumento de 1-1 millones de dólares. En estos gráficos, funciones exponenciales de la forma f ( x ) = a · b X aparecen como líneas rectas con pendiente igual al logaritmo de b . log-log gráficos escalar ambos ejes de forma logarítmica, lo que hace que las funciones de la forma f ( x ) = una · x k que se representan como líneas rectas con pendiente igual al exponente k . Esto se aplica en la visualización y el análisis de las leyes de potencia.
Psicología
Los logaritmos ocurren en varias leyes que describe la percepción humana: . ley de Hick propone una relación logarítmica entre el momento en individuos toman para la elección de una alternativa y el número de opciones que tienen la ley de Fitts predice que el tiempo requerido para mover rápidamente a una zona objetivo es una función logarítmica de la distancia al y el tamaño del objetivo. En psicofísica, la ley de Weber-Fechner propone una relación logarítmica entre el estímulo y la sensación como el real frente al peso percibido de un artículo de una persona está llevando. (Esta "ley", sin embargo, es menos preciso que los modelos más recientes, como la ley de potencia de Stevens.)
Los estudios psicológicos encontraron que los individuos matemáticamente poco sofisticados tienden a estimar cantidades logarítmica, es decir, que posicionan un número en una línea sin marcar de acuerdo con su logaritmo, de modo que 10 se posiciona tan cerca de 20 como 100 es a 200. El aumento de la comprensión matemática desplaza a esta una estimación lineal (posicionamiento 100 10x tan lejos).
Teoría de la probabilidad y la estadística
Logaritmos surgen en teoría de la probabilidad : la ley de los grandes números establece que, para que una moneda al aire, como el número de monedas-lanzamientos aumenta hasta el infinito, la proporción observada de cabezas se acerca a la mitad . Las fluctuaciones de esta proporción aproximadamente la mitad son descritos por la ley del logaritmo iterado.
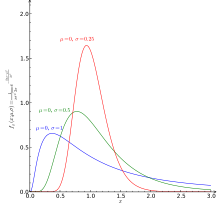
Logaritmos también ocurren en las distribuciones log-normal. Cuando el logaritmo de una variable aleatoria tiene una distribución normal , se dice que la variable a tener una distribución logarítmica normal. Distribuciones log-normal se encuentran en muchos campos, donde una variable se forma como el producto de muchas variables aleatorias independientes positivos, por ejemplo en el estudio de la turbulencia.
Los logaritmos son utilizados para la estimación de máxima verosimilitud de paramétricas modelos estadísticos. Para un modelo de este tipo, la función de probabilidad depende de al menos un parámetro que debe ser estimado. Un máximo de la función de probabilidad se produce en el mismo parámetro-valor como un máximo del logaritmo de la probabilidad (la " probabilidad de registro "), ya que el logaritmo es una función creciente. El diario de probabilidad es más fácil para maximizar, especialmente para las probabilidades multiplicadas para variables aleatorias independientes.
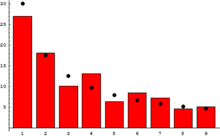
La ley de Benford describe la aparición de dígitos en muchos conjuntos de datos, tales como alturas de los edificios. Según la ley de Benford, la probabilidad de que el primer decimal dígitos de un elemento de la muestra de datos es d (de 1 a 9) es igual a log 10 ( d + 1) - log 10 ( d ), independientemente de la unidad de medida. Por lo tanto, aproximadamente el 30% de los datos se puede esperar que tenga 1 como primer dígito, inicio 18% con 2, etc. Cuentas examinan las desviaciones de la ley de Benford para detectar la contabilidad fraudulenta.
Complejidad computacional
Análisis de algoritmos es una rama de ciencias de la computación que estudia el comportamiento de los algoritmos (programas de computación para resolver un determinado problema). Los logaritmos son valiosos para describir algoritmos que dividen a un problema en otros más pequeños, y se unen a las soluciones de los subproblemas.
Por ejemplo, para encontrar un número en una lista ordenada, el algoritmo de búsqueda binaria comprueba la entrada media y procede con la media antes o después de la entrada medio si todavía no se encuentra el número. Este algoritmo requiere, en promedio, log 2 ( N ) comparaciones, donde N es la longitud de la lista. Del mismo modo, la fusionar algoritmo de ordenación ordena una lista sin ordenar al dividir la lista en dos mitades y clasificación de éstos antes de la fusión de los resultados. Merge algoritmos ordenar típicamente requieren un tiempo aproximadamente proporcional a N · log ( N ) . La base del logaritmo no se especifica aquí, ya que el resultado sólo cambia por un factor constante cuando se utiliza otra base. Un factor constante, por lo general se tomarán en cuenta para el análisis de algoritmos bajo la norma modelo de costo uniforme.
Una función f ( x ) se dice que crecen logarítmicamente si f ( x ) es (exactamente o aproximadamente) proporcional al logaritmo de x . (Descripciones biológicos de crecimiento del organismo, sin embargo, utilizan este término para una función exponencial.) Por ejemplo, cualquier número natural N se puede representar en forma binaria en no más de log 2 ( N ) + 1 Bits. En otras palabras, la cantidad de memoria necesaria para almacenar N crece logarítmicamente con N .
La entropía y el caos
La entropía es una medida ampliamente del trastorno de algún sistema. En termodinámica estadística , la entropía S de algún sistema físico se define como
La suma es sobre todos los estados posibles i del sistema en cuestión, tales como las posiciones de las partículas de gas en un contenedor. Además, p yo es la probabilidad de que el estado i se alcanza y k es la constante de Boltzmann. Del mismo modo, entropía en teoría de la información mide la cantidad de información. Si un destinatario del mensaje puede esperar una cualquiera de N posibles mensajes con igual probabilidad, entonces la cantidad de información transmitida por cualquiera de tales mensaje se cuantifica como log 2 ( N ) bits.
Exponentes de Lyapunov utilizan logaritmos para medir el grado de caoticidad de un sistema dinámico. Por ejemplo, para una partícula que se mueve en una mesa de billar ovalada, incluso pequeños cambios en las condiciones iniciales resultan en caminos muy diferentes de la partícula. Tales sistemas son caótica en una manera determinista, porque los pequeños errores de medición del estado inicial predeciblemente conducen a diferentes estados finales en gran medida. Al menos un exponente de Lyapunov de un sistema determinista caótica es positivo.
Fractales
Logaritmos se producen en las definiciones de la dimensión de los fractales . Los fractales son objetos geométricos que son auto-similar: piezas pequeñas se reproducen, al menos, más o menos, toda la estructura global. La triángulo de Sierpinski (en la foto) se puede cubrir con tres copias de sí mismo, cada uno con lados la mitad de la longitud original. Esto hace que la dimensión de Hausdorff de esta estructura de registro (3) / log (2) ≈ 1,58 . Otra noción basado en logaritmo de dimensión se obtiene contando el número de cajas necesarios para cubrir el fractal en cuestión.
Música
Logaritmos están relacionados con los tonos musicales y los intervalos. En temperamento igual, la relación de frecuencia depende sólo de que el intervalo entre dos tonos, no en la frecuencia específica, o el tono, de los tonos individuales. Por ejemplo, el nota A tiene una frecuencia de 440 Hz y si bemol tiene una frecuencia de 466 Hz. El intervalo entre la A y la B-plano es un semitono, como es la que existe entre bemol y B (frecuencia de 493 Hz). En consecuencia, las relaciones de frecuencia de acuerdo:
Por lo tanto, los logaritmos se pueden utilizar para describir los intervalos: un intervalo se mide en semitonos mediante la adopción de la base 2 1/12 logaritmo de la relación de frecuencia, mientras que la base de 2- 1/1200 logaritmo de la relación de frecuencia expresa el intervalo en centavos, centésimas de semitono. Este último se utiliza para la codificación más fino, ya que es necesario para no iguales temperamentos.
| Intervalo (Los dos tonos se reproducen al mismo tiempo) | Juego 1/12 tono | Juego Semitone | Sólo tercera mayor juego | Mayor tercera obra | Juego Tritone | Juego Octave |
| Relación Frecuencia r | 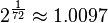 | 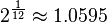 | 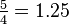 | ![\begin{align} 2^{\frac 4 {12}} & = \sqrt[3] 2 \\ & \approx 1.2599 \end{align}](../../images/2457/245704.png) | 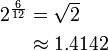 | 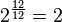 |
Correspondiente número de semitonos ![\log_{\sqrt[12] 2}(r) = 12 \log_2 (r)](../../images/2457/245707.png) | 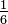 | 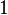 | 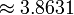 | 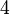 | 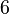 | 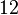 |
Correspondiente número de centavos ![\log_{\sqrt[1200] 2}(r) = 1200 \log_2 (r)](../../images/2457/245712.png) | 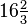 | 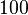 | 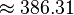 | 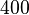 | 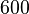 | 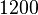 |
Teoría de los números
Logaritmos naturales están estrechamente vinculadas a contar los números primos (2, 3, 5, 7, 11, ...), un tema importante en la teoría de números . Para cualquier número entero x , la cantidad de números primos menores o iguales a x se denota π ( x ). La número primo teorema afirma que π ( x ) viene dado aproximadamente por
en el sentido de que la relación de π ( x ) y que se aproxima a la fracción 1 cuando x tiende a infinito. Como consecuencia, la probabilidad de que un número elegido al azar entre 1 y x es primo es inversamente proporcional al número de dígitos decimales de x . Un mucho mejor estimación de π ( x ) viene dada por la función integral logarítmica compensar Li ( x ), definida por
La Hipótesis de Riemann, uno de los más antiguos matemáticos abiertosconjeturas, se puede afirmar, en términos de la comparación de π (x) y Li (x). La Erdős-Kac teorema describe el número de distintosfactores primos también involucra el logaritmo natural.
El logaritmo de n factorial , n ! = 1 · 2 · ... · n , viene dada por
Esto puede ser usado para obtener la fórmula de Stirling, una aproximación de n ! para grandes n .
Las generalizaciones
Logaritmo complejo
Losnúmeros complejos ala solución de la ecuación
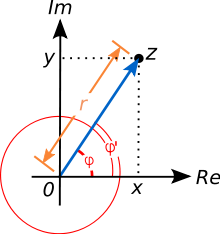
se llaman logaritmos complejos . Aquí, z es un número complejo. Un número complejo está representado comúnmente como z = x + iy , donde x y y son números reales y i es la unidad imaginaria . Un número de este tipo puede ser visualizado por un punto en el plano complejo , como se muestra a la derecha. La forma polar codifica un no-cero número complejo z por su valor absoluto , es decir, la distancia r al origen, y un ángulo entre la x eje y la línea que pasa por el origen y z . Este ángulo se llama el argumento de z . El valor absoluto r del z es
El argumento no se especifica de forma única por z : tanto φ y φ '= φ + 2π son argumentos de z porque la adición de 2π radianes o 360 grados para φ corresponde a "sinuoso" en torno al origen contra-reloj-sabio por un turno. El número complejo resultante es de nuevo z , como se ilustra a la derecha. Sin embargo, cumple exactamente un argumento varphi -π <φ y φ ≤ π . Se llama el argumento principal , que se denota Arg ( z ), con un capital A . (Una alternativa es la normalización 0 ≤ Arg ( z ) <2π .)
El uso defunciones trigonométricas seno ycoseno, o laexponencial compleja, respectivamente,ry φ son tales que tienen las siguientes identidades:
Esto implica que launa-ésimopoder deees igual az, en donde
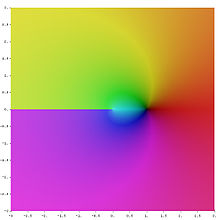
φ es el principal argumento Arg ( z ) y n es un entero arbitrario. Cualquier una se llama un complejo logaritmo de z . Hay infinitamente muchos de ellos, en contraste con el logaritmo de bienes definida de forma única. Si n = 0 , una se llama el valor principal del logaritmo, denotado Log ( z ). El principal argumento de cualquier número real positivo x es 0; por lo tanto, Log ( x ) es un número real y es igual a la verdadera logaritmo (natural). Sin embargo, las fórmulas anteriores para logaritmos de productos y poderes no no generalizan al valor principal del logaritmo complejo.
La ilustración de la derecha representa Log ( z ). La discontinuidad, es decir, el salto en el tono en la parte negativa de la x - o eje real, es causada por el salto del argumento principal allí. Este lugar se llama una rama cortada. Este comportamiento sólo se puede evitar dejando caer la restricción del rango de φ. Entonces el argumento de z y, en consecuencia, su logaritmo convertirse funciones con varios valores.
Inversas de otras funciones exponenciales
Exponenciación ocurre en muchas áreas de las matemáticas y su función inversa se refiere a menudo como el logaritmo. Por ejemplo, el logaritmo de una matriz es la función inversa (de varios valores) de la matriz exponencial. Otro ejemplo es el p logaritmo -adic, la función inversa de la p -adic exponencial. Ambos se definen a través de la serie de Taylor análogo al caso real. En el contexto de la geometría diferencial , el mapa exponencial asigna el espacio tangente en un punto de un colector a una vecindad de ese punto. Su inversa es también llamado el (o registro) mapa logarítmica.
En el contexto de grupos finitos exponenciación se da multiplicando repetidamente elemento de un grupobcon sí mismo. La logaritmo discreto es el número enteronresolver la ecuación
donde x es un elemento del grupo. Llevar a cabo la exponenciación se puede hacer de manera eficiente, pero el logaritmo discreto se cree que es muy difícil de calcular en algunos grupos. Esta asimetría tiene importantes aplicaciones en la criptografía de clave pública, como por ejemplo en el intercambio de claves Diffie-Hellman, una rutina que permite intercambios seguros de criptográficas teclas a través de canales de información sin garantía. logaritmo de Zac está relacionado con el logaritmo discreto en el grupo multiplicativo de no -Zero elementos de una campo finito.
Otras funciones inversas, logaritmos, como son el logaritmo doble ln (ln ( x )), el logaritmo-hiper-super-4 o (una ligera variación de los cuales se llama logaritmo iterado en informática), la función W de Lambert y el logit . Ellos son las funciones inversas de la función exponencial doble, tetración, de f ( w ) = nos w , y de la función logística, respectivamente.
Conceptos relacionados
Desde la perspectiva de la matemática pura, la identidad de registro ( cd ) = log ( c ) + log ( d ) expresa un isomorfismo de grupo entre positivos reales bajo la multiplicación y reales bajo adición. Funciones logarítmicas son los únicos isomorfismos continuas entre estos grupos. Por medio de que isomorfismo, la medida de Haar ( medida de Lebesgue) dx en los reales corresponde a la medida de Haar dx / x en los reales positivos. En complejas de análisis y geometría algebraica, formas diferencial de la forma df / f se conocen como formas con logarítmica polos.
La polilogaritmo es la función definida por
Está relacionado con el logaritmo natural por Li 1 ( z ) = ln (1 - z ) . Por otra parte, Li s (1) es igual a la función zeta ζ (Riemann s ).


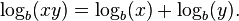
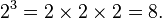
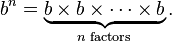
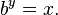
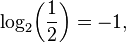
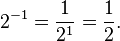
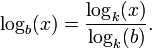
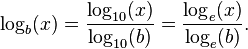
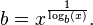
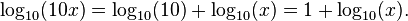
![\ Cos \, \ alpha \, \ cos \, \ beta = \ frac12 [\ cos (\ alpha + \ beta) + \ cos (\ alpha \ beta)]](../../images/2455/245585.png)
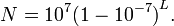
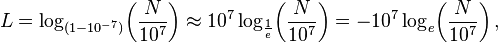
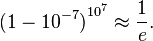
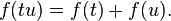
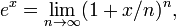
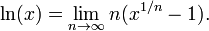
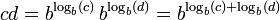
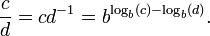
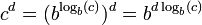
![\ Sqrt [d] {c} = c ^ {\ frac 1 d} = b ^ {\ frac {1} {d} \ log_b (c)}. \,](../../images/2456/245605.png)
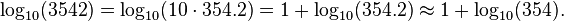
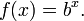
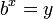
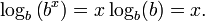
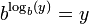
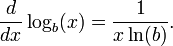
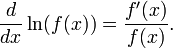
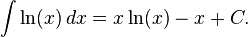
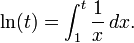
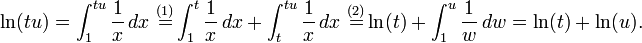

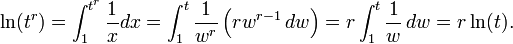
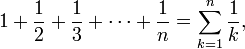
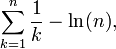
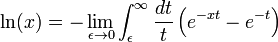
![\ Sqrt {-5+ \ sqrt [3] {3/13}}.](../../images/2456/245647.png)
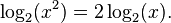
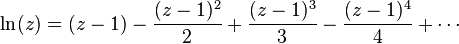
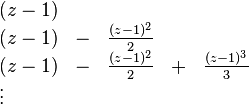
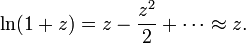
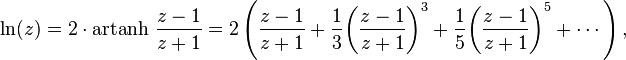
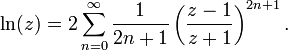
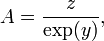
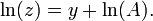
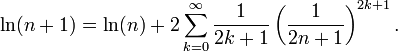
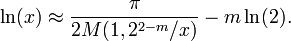
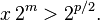

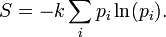



![\frac{466}{440} \approx \frac{493}{466} \approx 1.059 \approx \sqrt[12]2.](../../images/2457/245700.png)