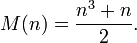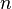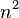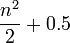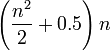Cuadrado mágico
Antecedentes
SOS Children han producido una selección de artículos de Wikipedia para escuelas desde 2005. ¿Quieres saber sobre el patrocinio? Ver www.sponsorachild.org.uk
En matemáticas recreativas, un cuadrado mágico de orden n es un arreglo de n ² números, por lo general distintos números enteros , en una plaza , de manera que los n números en todas las filas, todas las columnas y las dos diagonales suman la misma constante. Un cuadrado mágico normal contiene los números enteros de 1 a n ². El término "cuadrado mágico" también se utiliza a veces para referirse a cualquiera de los diversos tipos de cuadrada palabra.
Existen cuadrados mágicos normales para todos los pedidos n ≥ 1, excepto n = 2, aunque el caso n = 1 es trivial-se compone de una sola célula que contiene el número 1. El caso no trivial más pequeño, se muestra a continuación, es de orden 3.
La suma constante en cada fila, columna y diagonal se llama constante mágica o suma magia, M. La constante mágica de un cuadrado mágico normal, sólo depende de n y tiene el valor
Para cuadrados mágicos normales de orden n = 3, 4, 5, ..., las constantes mágicas son:
- 15, 34, 65, 111, 175, 260, ... (secuencia A006003 en OEIS ).
Historia de los cuadrados mágicos
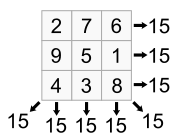
El cuadrado Lo Shu (3 x 3 cuadrado mágico)
La literatura china que data ya desde 650 aC cuenta la leyenda de Lo Shu o "desplazamiento del río Lo". En la antigua China , hubo una gran inundación. La gente trató de ofrecer un sacrificio al dios del río de una de las avenidas de los ríos, el río Lo, para calmar su ira. Entonces, surgió desde el agua una tortuga con una figura / patrón curioso en su concha; hubo puntos circulares de números que fueron dispuestos en un patrón de tres por tres de nueve rejilla de tal manera que la suma de los números en cada fila, columna y diagonal era el mismo: 15. Este número es también igual al número de días en cada de los 24 ciclos de la Año solar chino. Este patrón, en cierto modo, fue utilizado por la gente en el control del río.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
La Lo Shu Square, como el cuadrado mágico en el caparazón de tortuga se llama, es el único cuadrado mágico normal de orden tres de los cuales 1 es en la parte inferior y 2 se encuentra en la esquina superior derecha. Cada cuadrado mágico normal de orden tres se obtiene del Lo Shu por rotación o reflexión.
La Plaza de Lo Shu también se conoce como el cuadrado mágico de Saturno o Cronos. Su valor numérico se obtiene a partir de los trabajos del I Ching cuando el Trigramas se colocan en un orden dado en el primer mapa del río, la Ho Tu o río Amarillo . El Ho Tu produce 4 plazas de Hexagrams 8 x 8 en sus valores exteriores de 1 a 6, 2 a 7, de 3 a 8, y de 4 a 9, y estos cuadrados externos pueden añadirse después simétricamente entre sí para dar un cuadrado central interior de 5 a 10. Los valores centrales del Ho Tu son las del Lo Shu (así que trabajan juntos), ya que en el valor total de 15 x 2 (claro y oscuro) se encuentra el número de años en el ciclo de precesión equinoccial (12,960 x 2 = 25 920). El Ho Tu produce un total de 40 luz y 40 números oscuros llamados los días y las noches (la alternancia de luz y oscuridad), y un total de 8 x 8 x 8 hexagramas cuyo opuesto simétrico Además es igual a 8640, por lo tanto, cada valor de una plaza se llama una temporada, ya que es igual a 2160. 8640 es el número de horas en un año de 360 días, y 2160 años es igual a una eón (12 eones = 25.920 años).
Para validar los valores contenidos en los mapas 2 de río (Ho Tu y Lo Shu) el I Ching ofrece números del Cielo y de la Tierra que son el 'original Trigramas' (padre y madre) de 1 a 10. El cielo o un trigrama con toda ininterrumpida líneas (líneas claras - yang) tienen números impares 1,3,5,7,9, y la Tierra un trigrama con todas las líneas rotas tienen números pares 2,4,6,8,10. Si cada una de las líneas del trigrama se le da un valor de multiplicar el número de los Cielos y de la Tierra, entonces el valor de cada línea en el cielo 1 sería 1 + 2 + 3 = 6, y su socio en el Ho Tu de tierra 6 sería 6 + 12 + 18 = 36, estos 2 'original Trigramas "con ello producir 6 Trigramas más (o los niños en todas sus combinaciones) - y cuando las secuencias de Trigramas son colocados en ángulos rectos entre sí producen un cuadrado de 8 x 8 de hexagramas (o cubos) que cada uno tiene 6 líneas de valores. Desde este punto sencilla la compleja estructura de las matemáticas evoluciona como una progresión hexadecimal, y es el hexágono que es el enlace a la tortuga o concha de tortuga. En los textos chinos del I Ching la luna es un símbolo de agua (oscuridad) cuyas transformaciones o cambios crear la luz o el fuego - el valor oscuro 6 crea la luz cuando su número se incrementa en 1. Este mismo principio se puede encontrar en los calendarios antiguos tales como el Egipcia, como el año de 360 días de 8640 horas se dividió por 72 para producir los 5 días adicionales o 120 horas en el que nacieron los dioses. Se necesitan 72 años para que los cielos se muevan 1 grado a través de su precesión.
Significado cultural de los cuadrados mágicos
Los cuadrados mágicos han fascinado a la humanidad a lo largo de los siglos, y han existido por más de 4.000 años. Se encuentran en una serie de culturas, incluyendo Egipto y la India, grabado en piedra o metal y desgastado como talismanes, la creencia es que los cuadrados mágicos tenían astrológicas y adivinatorias cualidades, su asegurando la longevidad y la prevención de enfermedades uso.
El Kubera-Kolam es una pintura planta utilizada en la India, que está en la forma de un cuadrado mágico de orden tres. Es esencialmente la misma que la cuadrícula Lo Shu, pero con 19 añadió a cada número, dando una constante mágica de 72.
| 23 | 28 | 21 |
| 22 | 24 | 26 |
| 27 | 20 | 25 |
Saudita
Cuadrados mágicos eran conocidos Los matemáticos árabes, posiblemente ya en el siglo séptimo, cuando los árabes se metió en contacto con la cultura de la India o del sur de Asia, y aprendieron matemáticas y astronomía de la India, incluyendo otros aspectos de la matemática combinatoria . También se ha sugerido que la idea vino a través de China. Los primeros cuadrados mágicos de orden 5 y 6 aparecen en una enciclopedia de Bagdad alrededor de 983 dC, la Rasa'il Ihkwan al-Safa (la Enciclopedia de la Brethern de pureza); cuadrados mágicos simples eran conocidos por varios matemáticos árabes anteriores.
El matemático árabe Ahmad al-Buni, quien trabajó en los cuadrados mágicos alrededor de 1200 dC, atribuye propiedades místicas a ellos, aunque no se conocen los detalles de estas supuestas propiedades. También hay referencias a la utilización de los cuadrados mágicos en los cálculos astrológicos, una práctica que parece haberse originado con los árabes.
India
Un cuadrado mágico temprana conocida en la India se encuentra en Khajuraho en la Parshvanath Templo Jain. Data del siglo 10.
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Esto se conoce como el Chautisa Yantra, ya que cada sub-cuadrado sumas a 34.
Europa
En 1300, basándose en el trabajo de los Emiratos Al-Buni, erudito griego bizantino Manuel Moschopoulos escribió un tratado matemático sobre el tema de los cuadrados mágicos, dejando de lado el misticismo de sus predecesores. Moschopoulos se cree que es el primer occidental que han escrito sobre el tema. En la década de 1450 el italiano Luca Pacioli estudió cuadrados mágicos y se recoge un gran número de ejemplos.
En alrededor de 1510 Heinrich Cornelius Agrippa escribió De Oculta Philosophia, aprovechando la Hermética y obras mágicas de Marsilio Ficino y Pico della Mirandola, y en él se explayó sobre las virtudes mágicas de siete cuadrados mágicos de orden 3 a 9, cada uno asociado a uno de los astrológicos planetas. Este libro fue muy influyente en toda Europa hasta que el contra-reforma, y los cuadrados mágicos de Agripa, a veces llamado Kameas , se siguen utilizando en la magia ceremonial moderna de la misma manera que él primero prescribe.
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
El uso más común para estos Kameas es proporcionar un patrón sobre la cual construir la sellos de espíritus, ángeles o demonios; las letras del nombre de la entidad se convierten en números, y las líneas se trazan a través del patrón que estos números sucesivos hacen en el kamea. En un contexto mágico, el cuadrado mágico término también se aplica a una variedad de plazas de palabras o números cuadrados encontraron en la mágica grimorios, incluyendo algunos que no sigue ningún patrón obvio, e incluso los que tienen diferentes números de filas y columnas. Por lo general, están destinadas para su uso como talismanes. Por ejemplo, los siguientes cuadrados son: La Cuadrado Sator, una de las plazas más famosas de magia que se encuentra en una serie de libros mágicos incluyendo la Clave de Salomón; una plaza "para superar la envidia", de El Libro de la energía; y dos plazas de El Libro de la Magia Sagrada de Abramelin el Mago, el primero en provocar la ilusión de un magnífico palacio a aparecer, y el segundo que se lleva en la cabeza de un niño durante una angelical invocación:
|
|
|
|
Cuadrado mágico de Albrecht Dürer

La plaza orden-4 magia en Grabado de Alberto Durero Melancolía I se creía que era el primer visto en el arte europeo. Es muy similar a Plaza de Yang Hui, que fue creado en China alrededor de 250 años antes de la época de Durero. La suma 34 se puede encontrar en las filas, columnas, diagonales, cada uno de los cuadrantes, el Centro de cuatro plazas, los cuadrados de las esquinas, los cuatro números exteriores en sentido horario desde las esquinas (3 + 8 + 14 + 9) y así mismo los cuatro contador -clockwise (las ubicaciones de cuatro reinas en las dos soluciones de la 4 reinas rompecabezas ), Los dos conjuntos de cuatro números simétricos (2 + 8 + 9 + 15 + 3 y 5 + 12 + 14) y la suma de las dos entradas medias de las dos columnas y filas exteriores (por ejemplo, 5 + 9 + 8 + 12 ), así como varios cuartetos en forma de cometa, por ejemplo, 3 + 5 + 11 + 15; los dos números en el medio de la fila inferior dan la fecha del grabado: 1514. Melancolía de Durero que juega un papel clave en el ladrón de arte, una novela de Noah Charney (Atria, 2007).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
El cuadrado mágico Sagrada Família

La fachada de la Pasión de la La Sagrada Familia en Barcelona, diseñado por el escultor Josep Subirachs, cuenta con un cuadrado de 4 × 4 mágica:
La constante mágica del cuadrado es de 33 años, la edad de Jesús en el momento de la Pasión. Estructuralmente, es muy similar a la del cuadrado mágico Melancholia, pero ha tenido los números en cuatro de las células reducidas por 1.
| 1 | 14 | 14 | 4 |
| 11 | 7 | 6 | 9 |
| 8 | 10 | 10 | 5 |
| 13 | 2 | 3 | 15 |
Si bien tener el mismo patrón de suma, esto no es un cuadrado mágico normal, como antes, como dos números (10 y 14) se duplican y dos (12 y 16) están ausentes, en su defecto el 1 → regla n².
Tipos de cuadrados mágicos y su construcción
Hay muchas maneras de construir cuadrados mágicos, pero el estándar (y más sencilla) manera es seguir ciertas configuraciones / fórmulas que generan patrones regulares. Existen cuadrados mágicos para todos los valores de n, con una sola excepción - es imposible construir un cuadrado mágico de orden 2. Los cuadrados mágicos se pueden clasificar en tres tipos: extraño, incluso doblemente (n divisible por cuatro) y por separado, incluso (n incluso, pero no es divisible por cuatro). Cuadrados impares y doblemente incluso mágicas son fáciles de generar; la construcción de solos incluso cuadrados mágicos es más difícil, pero existen varios métodos, incluyendo la Método LUX para los cuadrados mágicos (debido a John Horton Conway) y el Método Strachey para los cuadrados mágicos.
La teoría de grupos también se utilizó para la construcción de nuevas cuadrados mágicos de un orden dado de uno de ellos, por favor ver .
| ¿Cuántas n × n cuadrados mágicos para n> 5? |
El número de diferentes n × n mágicos cuadrados para n de 1 a 5, sin contar las rotaciones y reflexiones:
- 1, 0, 1, 880, 275 305 224 (secuencia A006052 en OEIS ).
El número para n = 6 se ha estimado en 1,7745 × 10 19.
Un método para construir un cuadrado mágico de orden impar
A partir de la columna central de la primera fila con el número 1, el movimiento fundamental para el llenado de los cuadrados es diagonal hacia arriba y la derecha, un paso a la vez. Si se encuentra una plaza llena, uno se mueve verticalmente hacia abajo una casilla en su lugar, a continuación, continuar como antes. Cuando un movimiento dejaría la plaza, que se envuelve alrededor de la última fila o la primera columna, respectivamente.
Patrones similares también se pueden obtener partiendo de otros cuadrados.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Las siguientes fórmulas ayudan a construir cuadrados mágicos de orden impar
| ||||||||||||
* Las raíces cuadradas son más fáciles de calcular que las raíces cúbicas
Ejemplo:
| ||||||||||||
El "Número medio" está siempre en la parte inferior diagonal izquierda a la superior derecha.
El "último número" es siempre opuesto al número 1 en una columna o fila exterior.
Un método para construir un cuadrado mágico de orden doblemente incluso
Doblemente incluso significa que n es un múltiplo par de un número entero par; o 4p, donde p es un número entero. por ejemplo, 4, 8, 12
Patrón genérico
Todos los números se escriben en orden de derecha a izquierda a través de cada fila, a su vez, a partir de la esquina superior izquierda. Los números son entonces retenidas ya sea en el mismo lugar o intercambiarse con sus números diametralmente opuestos en un cierto patrón regular. En el cuadrado mágico de orden cuatro, los números en las cuatro casillas centrales y un cuadrado en cada esquina se mantienen en el mismo lugar y los otros se intercambian con sus números diametralmente opuestas.
Una construcción de un cuadrado mágico de orden 4
Ir a la izquierda a la derecha a través de la plaza llenando conteo y llenado en sólo en las diagonales. Luego continuar yendo a la izquierda a la derecha desde la parte superior izquierda de la tabla y rellenar la cuenta regresiva desde 16 o n². Como se muestra abajo.
|
| ||||||||||||||||||||||||||||||||||||||||
El medjig-método de construir cuadrados mágicos de orden par n> 4
Este método lúdico se basa en un juego matemático publicada 2006 llamado medjig (autor: Willem Barink, editor: Philos-Spiele). Las piezas del rompecabezas medjig son cuadrados divididos en cuatro cuadrantes en los que los números 0, 1, 2 y 3 están diseminados en todas las secuencias. Hay 18 plazas, cada secuencia se produce 3 veces. El objetivo del puzle es tomar 9 cuadrados de la recogida y organizarlos en un 3 x 3 "medjig cuadrados" de una manera tal que la serie, columnas y diagonales formadas por los cuadrantes, muestran la suma de 9.
La forma medjig de construcción de un cuadrado mágico de orden 6 es la siguiente. Organizar un cuadrado de 3 x 3 medjig (por comodidad este tiempo usted puede elegir ilimitado desde toda la colección). Luego tomar el clásico cuadrado mágico conocido 3 x 3 y dividir todos los campos de la misma en cuatro cuadrantes. Siguiente llenar estos cuadrantes con el número original y sus tres módulo-9 números hasta 36, siguiendo el patrón de la solución medjig. Si lo hace, el campo original con el número 8 se obtienen las cuatro subcampos con los números 8 (= 8 + 0x9), 17 (= 8 + 1x9), 26 (= 8 + 2x9) y 35 (= 8 + 3x9), el campo con el número 3 se obtienen los números 3, 12, 21 y 30, etc ... Ver ilustración abajo.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De la misma manera se puede construir un cuadrado mágico de orden 8. Usted primero tiene que construir una solución medjig 4 x 4 (suma de todas las series, columnas y diagonales 12). Y luego ampliar por ejemplo el conocido Durero 4 x 4 cuadrado mágico de módulo-16 a 64. Para la construcción de un cuadrado mágico de orden 10 usted tiene que arreglar una solución medjig 5 x 5, para los que se necesitan dos conjuntos de piezas medjig . Respecto del orden de 12 puede simplemente duplicar horizontal y verticalmente una solución medjig 3 x 3 y luego ampliar módulo-36-144 de la plaza para 6 mágica hecha anteriormente. Orden 16 va de la misma manera.
La construcción de cuadrados panmagic
Cualquier número p en la plaza de orden n se puede escribir únicamente en la forma p = an + r, con r elegido a partir de {1, ..., n}. Tenga en cuenta que debido a esta restricción, a y r no son el cociente y el resto de la división por p n habitual. En consecuencia, el problema de la construcción se puede dividir en dos problemas más fáciles de resolver. Así, la construcción de dos emparejan rejillas cuadradas de orden n panmagic satisfactoria propiedades, una para los números a (0, ...., N-1), y otra para los números r (1, ...., N). Esto requiere una gran cantidad de desconcertante, pero se puede hacer. Cuando tiene éxito, ellos se combinan en uno - panmagic - cuadrado. Van den Essen y muchos otros supone ésta fue también la forma en que el gran Benjamin Franklin (1706-1790) construyó sus famosas plazas franklin. Tres cuadrados panmagic se muestran a continuación. Las dos primeras plazas se han construido abril de 2007 por Barink, la tercera es unos años mayor, y viene de Donald Morris, que utiliza, como él supone, la forma franklin de construcción.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
El orden 8 satisface cuadrados todas las propiedades panmagic, incluidos los de Franklin. Se compone de 4 unidades 4x4 perfectamente panmagic. Tenga en cuenta que tanto para 12 plazas muestran la propiedad de que cualquier fila o columna se pueden dividir en tres partes con una suma de 290 (= 1/3 de la suma total de una fila o columna). Esta propiedad compensa la ausencia de la propiedad franklin panmagic más estándar que cualquier medio fila o columna muestra la suma de 1/2 del total. Para el resto de las 12 plazas para difieren un cuadrado lot.The Barink 12x12 se compone de 9 unidades 4x4 perfectamente panmagic, por otra parte los 4 números consecutivos comenzando en cualquier lugar extraño en una fila o columna de mostrar una suma de 290. El cuadrado 12x12 Morris carece estas propiedades, pero por el contrario muestra franklindiagonals constantes. Para una mejor comprensión de la CONSTRUCCIÓN descomponer las plazas como se describió anteriormente, y ver cómo se ha hecho. Y tenga en cuenta la diferencia entre las construcciones Barink por una parte, y la construcción Morris / Franklin en el otro lado.
En las Matemáticas de libros en el Time-Life Science Library Series, se muestran los cuadrados mágicos de Euler y Franklin. Franklin diseñó este uno para que cualquier subconjunto de cuatro cuadrados (cualquiera de los cuatro cuadrados contiguos que forman un cuadrado más grande, o cualquiera de los cuatro plazas equidistantes del centro) total de 130. En la plaza de Euler, las filas y columnas de cada total de 260, y la mitad que en total 130 - y un ajedrez caballero, por lo que sus movimientos en forma de L en la plaza, puede tocar los 64 cuadros en orden numérico consecutivo.
La construcción de un cuadrado mágico usando algoritmos genéticos
Un cuadrado mágico se puede construir usando algoritmos genéticos. Este es un proceso de ensayo y error elegante en el que se genera una población inicial de los cuadrados mágicos con valores aleatorios. Las eficacias de estos cuadrado mágico individuo se calculan con base en el "aplanamiento" del cuadrado mágico, es decir, el grado de desviación en las sumas de las filas, columnas y diagonales. La población de los cuadrados mágicos se cruzarse (valores de cambio) de una manera coherente con la genética, sobre la base de la puntuación de la aptitud de los cuadrados mágicos. Por lo tanto, los cuadrados mágicos con una puntuación mayor aptitud tendrán una mayor probabilidad de reproducirse. En el proceso de entrecruzamiento, donde los cuadrados mágicos intercambian sus valores, se introduce un factor de mutación, imitando mutación genética en la naturaleza. Esta mutación se incluye o excluye, naturalmente, de la solución en función de su contribución a la aptitud del cuadrado mágico. La próxima generación de la población cuadrado mágico se calcula de nuevo por su estado físico, y este proceso continúa hasta que se haya encontrado una solución.
Las generalizaciones
Restricciones adicionales
Ciertas restricciones adicionales pueden ser impuestas a los cuadrados mágicos. Si no sólo las diagonales principales, sino también las diagonales rotas suman a la constante mágica, el resultado es una plaza panmagic. Si elevar cada número a ciertos poderes produce otro cuadrado mágico, el resultado es un bimagic, una trimagic, o, en general, una plaza multimagic.
Diferentes limitaciones
A veces las reglas de los cuadrados mágicos son relajado, por lo que sólo las filas y columnas, pero no necesariamente las diagonales suman la constante mágica. En heterosquares y cuadrados antimagia, los 2 n + 2 sumas deben ser todos diferentes.
Otras operaciones
En lugar de agregar los números en cada fila, columna y diagonal, se puede aplicar alguna otra operación. Por ejemplo, un cuadrado mágico multiplicativo tiene un producto constante de números.
|
| ||||||||||||||||||||||||||||||||
Otras formas de magia
Otras formas que cuadrados pueden ser considerados, resultante, por ejemplo, en las estrellas mágicas y hexágonos mágicos. Subiendo en los resultados de la dimensión en cubos mágicos, tesseracts mágicos y otros hipercubos mágicos.
Edward Shineman, de renombre internacional forma construccionista magia, ha desarrollado un nuevo diseño en forma de diamantes mágicos. Él ha hecho muchas de ellas con fines conmemorativos e históricos, y también ha experimentado con otro autónomo doble rectángulo / combinaciones cuadrados, cifras "aligeramiento" en forma de L, y más. Los diamantes se han hecho en honor de los acontecimientos y las personas que van de Tiger Woods a Ronald Reagan, del aniversario de la Universidad de Cornell para los cumpleaños familiares especiales. Varias de sus obras han aparecido en libros cuadrados mágicos, así como varias publicaciones en el diario de la matemática recreativa. Una serie de sus contribuciones mágicos se puede encontrar en eds-magic-squares.com.
Extensiones combinadas
Uno puede combinar dos o más de las extensiones anteriores, resultando en objetos tales como hipercubos multimagic multiplicativos. Poco parece saberse sobre este tema.
Problemas relacionados
Con los años, muchos matemáticos, incluyendo Euler y Cayley han trabajado en los cuadrados mágicos, y descubrió las relaciones fascinantes.
Cuadrado mágico de los números primos
Rudolf Ondrejka (1928-2001) descubrió el siguiente cuadrado mágico 3x3 de números primos , en este caso nueve Chen primos:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
La Green-Tao teorema implica que hay arbitrariamente grandes cuadrados mágicos que consisten de números primos.
n-Queens problema
En 1992, Demirörs, Rafraf y Tanik publicaron un método para convertir algunos cuadrados mágicos en Soluciones de N-reinas, y viceversa.
Fecha cuadrado mágico
Un cuadrado fecha mágica es un cuadrado de 4 × 4 mágico en el que los números en una fecha determinada (por ejemplo, 15 de abril, 1707) se utilizan para construir la primera fila (4, 15, 17, 07). La constante mágica (M) de un 4 × 4 cuadrado mágico "normal" es 34. Si los cuatro números en una fecha no se suman a 34, no podemos construir un cuadrado mágico "normal" para esa fecha. En el ejemplo anterior, M = 43:
| 4 | 15 | 17 | 07 |
| 5 | 19 | 13 | 6 |
| 20 | 9 | 2 | 12 |
| 14 | 0 | 11 | 18 |
La única diferencia entre un cuadrado mágico y un cuadrado mágico fecha es que, en una fecha mágica repetición cuadrada de números que no está permitido en cualquier fila, excepto la primera, mientras que en un cuadrado mágico "normal", la repetición no está permitido en cualquier fila .
Número / Plaza de Word Magic
A / Palabra cuadrado combinación mágica Número se construye con las tres reglas siguientes:
- Hacer un cuadrado mágico normal de orden 3 utilizando cualquier número.
- Cuente el número de letras de cada número y reemplazar el número con esta cuenta.
- La nueva plaza debe ser también la magia.
Un ejemplo de un cuadrado como se muestra a continuación:
|
|
| ||||||||||||||||||||||||||||||||||||
Problema Esperadnos-Escott
Por una extraña coincidencia, el cuadrado de 3 × 3 mágica contiene una solución al Problema Esperadnos-Escott.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Preparar dos conjuntos de números del cuadrado mágico anteriormente mediante la combinación de los números de las últimas filas y últimas columnas en las direcciones marcha y contramarcha:
- {492, 276, 618, 834}
- {294, 438, 816, 672}.
Quedaos-Escott Solución:
- 492 1 276 + 1 + 618 + 1 = 834 1 294 1 438 + 1 + 816 + 1 672 1
- 492 2 + 2 + 276 618 2 + 2 = 834 294 2 438 + 2 + 2 + 816 672 2
- 492 3 + 3 + 276 618 3 + 834 = 3 294 438 3 + 3 + 3 + 816 672 3.
Cuadrados mágicos de la literatura contemporánea
En el capítulo 2 de El Gran Cerebro es Volver por John D. Fitzgerald, Tom, alias el "gran cerebro", recuerda haber sido informado por un profesor sobre un cuadrado mágico. Después de trabajar en él durante tres días, él viene con la Orden 3, Sum 15 cuadrado. A continuación, configura el "juego de los números", deteniendo a sus amigos y explicar el concepto, cobrando 10 centavos para jugar con un premio de 50 centavos para cualquiera que pueda resolverlo dentro de dos días, la entrega de una hoja con la cuadrícula de 3 * 3 y los números del uno al nueve de cada jugador, y dar permiso a todos los participantes que reciben la ayuda de sus padres. Pensando que va a ser fácil, los 20 niños presentes incluyendo a su hermano Juan (el narrador) optan por jugar y darle un centavo. John muestra a su padre, el único graduado de la universidad en la ciudad. Su padre explica que lo primero que debe hacer es hacer una lista de todas las combinaciones de tres números del 1 al 9, que suman 15, con exclusión de aquellos en los que un número se utiliza más de una vez. Entonces (que muestra una falta de conocimientos sobre el tema) que dice que hay que "seguir intentando las diferentes combinaciones hasta obtener la respuesta correcta." Juan hace la lista y pasa cada momento libre que tiene en los próximos dos días tratando de poner las combinaciones entre sí, sin éxito. Su padre le dice que lo haga por eliminación y comenzar con las tres plazas en el centro, pero no dio más detalles. Después de dos días, nadie lo ha resuelto, y algunos creen que no se puede hacer. Pero cuando expire el plazo y no hay ganadores, Tom revela la respuesta.
En La novela de Steve Martin El placer de mi compañía, el personaje principal Daniel Pecan Cambridge construye cuadrados mágicos como una forma de relajarse.