Método de Monte Carlo

El método de Monte Carlo puede ilustrarse como un juego de acorazado. Primero un jugador hace algunos disparos al azar. A continuación, el jugador aplica algoritmos (es decir. Un buque de guerra es de cuatro puntos en dirección vertical u horizontal). Finalmente basa en los resultados del muestreo aleatorio y el algoritmo que el jugador puede determinar las ubicaciones probables de los barcos del otro jugador.

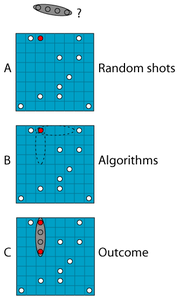
Un método de Monte Carlo es una computacional algoritmo que se basa en repetida muestreo aleatorio para calcular sus resultados. Métodos de Monte Carlo se utilizan a menudo cuando simulando físicos y matemáticos de sistemas. Debido a su dependencia de cálculo repetido y azar o números pseudo-aleatorios, métodos de Monte Carlo son los más adecuados para el cálculo de un ordenador . Métodos de Monte Carlo tienden a ser utilizados cuando no es posible o imposible calcular un resultado exacto con una algoritmo determinista.

El término Monte Carlo fue acuñado en la década de 1940 por los físicos que trabajan en proyectos de armas nucleares en el Laboratorio Nacional de Los Álamos.

Visión de conjunto

No existe un único método de Monte Carlo; en cambio, el término describe una clase grande y ampliamente utilizado de enfoques. Sin embargo, estos enfoques tienden a seguir un patrón particular:

1. Definir un dominio de las posibles entradas.
2. Generar insumos al azar de dominio, y le realizará un cálculo determinista en ellos.
3. Agregar los resultados de los cálculos individuales en el resultado final.

Por ejemplo, el valor de π se puede aproximar utilizando un método de Monte Carlo. Dibuja un cuadrado en el suelo, luego inscribir un círculo dentro de ella. Ahora, dispersar algunos pequeños objetos (por ejemplo, granos de arroz o arena) en toda la plaza. Si se dispersan los objetos uniformemente, a continuación, la proporción de los objetos dentro del círculo debe ser de aproximadamente π / 4, que es la relación del área del círculo al área de la plaza. Por lo tanto, si contamos el número de objetos en el círculo, multiplicar por cuatro, y se divide por el número de objetos en la plaza, nos pondremos en contacto una aproximación de π.

Observe cómo la aproximación π sigue el patrón general de los algoritmos de Monte Carlo. En primer lugar, se define un dominio de entradas: en este caso, es el cuadrado que circunscribe nuestro círculo. A continuación, generamos entradas al azar (esparcen granos individuales dentro de la plaza), a continuación, realizar un cálculo en cada entrada (prueba si cae dentro del círculo). Al final, agregamos los resultados en nuestro resultado final, la aproximación de π. Tenga en cuenta, también, otras dos propiedades comunes de los métodos de Monte Carlo: la dependencia de la computación en buenos números aleatorios, y su lenta convergencia a una mejor aproximación que se muestrean más puntos de datos. Si sólo dejamos caer nuestros granos en el centro del círculo, puede ser que simplemente se acumulan en una pila dentro del círculo: no se distribuyen de manera uniforme, por lo que nuestra aproximación serán muy lejos. Pero si se distribuyen uniformemente, entonces los más granos dejamos caer, más precisa nuestra aproximación de π se convertirá.

Historia

Métodos de Monte Carlo se practicaban originalmente bajo nombres más genéricos como "muestreo estadístico". El nombre de "Monte Carlo" fue popularizado por investigadores de física Stanislaw Ulam, Enrico Fermi, John von Neumann , y Nicholas Metropolis, entre otros; el nombre es una referencia a un famoso casino en Mónaco que el tío de Ulam pediría prestado dinero para jugar en. El uso de aleatoriedad y la naturaleza repetitiva del proceso son análogas a las actividades realizadas en un casino.

Métodos aleatorios de formas de cálculo y experimentación (generalmente se considera de simulación estocástica) puede ser discutible remonta a los primeros pioneros de la teoría de la probabilidad (véase, por ejemplo, Aguja de Buffon, y el trabajo en pequeñas muestras por William Gosset), pero se trazan más específicamente a la era de la computación pre-electrónica. La diferencia general usualmente descrito sobre una forma de Monte Carlo de simulación es que sistemáticamente "invierte" el típico modo de simulación, el tratamiento de problemas deterministas encontrando primero un análogo probabilístico. Los métodos anteriores de simulación y muestreo estadístico general hizo lo contrario: el uso de simulación para probar un problema determinista previamente comprendido. Aunque existen ejemplos de un enfoque "invertida" históricamente, no se consideraron un método general hasta que la popularidad del método de propagación Monte Carlo.

Quizás el más famoso fue el uso temprano de Enrico Fermi en 1930, cuando se utiliza un método aleatorio para calcular las propiedades de la recién descubierta de neutrones . Métodos de Monte Carlo fueron fundamentales para el simulaciones requeridas para la Proyecto Manhattan, aunque fueron severamente limitado por las herramientas computacionales en el momento. Por lo tanto, no fue hasta después de las computadoras electrónicas se construyeron primero (a partir de 1945) que los métodos de Monte Carlo comenzó a ser estudiado en profundidad. En la década de 1950 que se utilizaron en Los Alamos para el trabajo temprano en relación con el desarrollo de la bomba de hidrógeno, y se convirtió popularizó en los campos de la física , química física, y la investigación de operaciones . La Rand Corporation y la Fuerza Aérea de Estados Unidos fueron dos de las principales organizaciones responsables de la financiación y difusión de información sobre los métodos de Monte Carlo durante este tiempo, y comenzaron a encontrar una amplia aplicación en muchos campos diferentes.

Usos de los métodos de Monte Carlo requieren grandes cantidades de números aleatorios, y fue su uso que estimuló el desarrollo de generadores de números pseudoaleatorios, que eran mucho más rápido de usar que las tablas de números aleatorios que se habían utilizado anteriormente para el muestreo estadístico.

Aplicaciones

Métodos de simulación de Monte Carlo son especialmente útiles en los sistemas de estudiar con un gran número de grados acoplados de la libertad, como líquidos, materiales desordenados, sólidos fuertemente acoplados, y estructuras celulares (ver celular modelo de Potts). En términos más generales, métodos de Monte Carlo son útiles para los fenómenos de modelado con significativa incertidumbre en los insumos, como el cálculo de riesgo en los negocios (para su uso en la industria de seguros, consulte modelación estocástica). Un uso clásico es para la evaluación de integrales definidas , en particular integrales multidimensionales con condiciones de contorno complicadas.

Métodos de Monte Carlo en las finanzas a menudo se utilizan para calcular el valor de las empresas, para evaluar las inversiones en proyectos a nivel corporativo o para evaluar los derivados financieros. El método de Monte Carlo se destina para los analistas financieros que quieren construir modelos estocásticos o probabilísticos financieros en oposición a los modelos estáticos y deterministas tradicionales.

Métodos de Monte Carlo son muy importantes en física computacional, química física, y afines campos aplicados, y tienen diversas aplicaciones, desde complicado cromodinámica cuántica cálculos para el diseño escudos de calor y formas aerodinámicas.

Métodos de Monte Carlo también han demostrado su eficacia en la solución de ecuaciones diferenciales acopladas integrales de los campos de radiación y el transporte de energía, y por lo tanto estos métodos se han utilizado en cálculos de iluminación global que producen imágenes fotorrealistas de modelos 3D virtuales, con aplicaciones en los videojuegos , la arquitectura , diseño, generados por computadora películas , efectos especiales en el cine, los negocios, la economía y otros campos.

Métodos de Monte Carlo son útiles en muchas áreas de las matemáticas computacionales, donde una elección afortunada puede encontrar el resultado correcto. Un ejemplo clásico es Algoritmo de Rabin para las pruebas de primalidad: para cualquier n que no es primo, un x aleatorio tiene al menos un 75% de probabilidades de probar que n no es primo. Por lo tanto, si n no es primo, pero x dice que podría ser, hemos observado a lo sumo un evento 1-en-4. Si 10 x diferentes al azar dicen que "n es, probablemente, el primer" cuando no lo es, hemos observado un caso de uno en un millón. En general, un algoritmo de Monte Carlo de este tipo produce una respuesta correcta con una garantía de n es compuesto, yx lo demuestra que sí, pero otra sin, pero con una garantía de no obtener esta respuesta cuando se equivoca demasiado a menudo - en este caso, como máximo el 25% del tiempo. Ver también Algoritmo de Las Vegas para una relacionada, pero diferente, idea.

Las áreas de aplicación

Las áreas de aplicación incluyen:

• Gráficos, en particular para trazado de rayos; una versión de la Algoritmo de Metropolis-Hastings también se utiliza para el trazado de rayos en donde se conoce como Transporte ligero Metropolis
• Transporte ligero Modelado en tejido biológico
• Métodos de Monte Carlo en finanzas
• La ingeniería de confiabilidad
• En recocido simulado para la estructura de la proteína de predicción
• En la investigación dispositivo semiconductor, para modelar el transporte de portadores de corriente
• Ciencias ambientales, que trata de la conducta contaminante
• Método de Monte Carlo en física estadística; en particular, Monte Carlo de modelado molecular como una alternativa para computacional dinámica molecular.
• Búsqueda y Rescate y Contra-contaminación. Modelos utilizados para predecir la deriva de una balsa salvavidas o el movimiento de una mancha de petróleo en el mar.
• En Diseño probabilístico para simular y comprender los efectos de la variabilidad
• En La química física, sobre todo para las simulaciones que implican agrupaciones atómicas
• En ciencias de la computación
  • Algoritmo de Las Vegas
  • LURCH
  • Computer Go
• Modelando el movimiento de los átomos de impurezas (o iones) en los plasmas en existente y tokamaks (por ejemplo: DIVIMP).
• En experimental de física de partículas , para el diseño Detectores, la comprensión de su comportamiento y comparando los datos experimentales a la teoría
• Códigos de la física nuclear y de partículas utilizando el método de Monte Carlo:
  • GEANT - Simulación del CERN de partículas de alta energía que interactúan con un detector.
  • CompHEP, PYTHIA - generadores de Monte-Carlo de colisiones de partículas
  • MCNP (X) - Códigos de transporte de radiación de LANL
  • EGS - Código de simulación de Stanford para el transporte acoplado de electrones y fotones
  • Herramienta de Monte Carlo del LLNL para cálculos de dosis de radioterapia - PEREGRINO
  • BEAMnrc - sistema de código de Monte Carlo para modelar fuentes de radioterapia ( De LINAC)
  • PENELOPE - Monte Carlo para el transporte acoplado de fotones y electrones, con aplicaciones en la radioterapia
  • MONJE - código de Serco Assurance para el cálculo de k-efectiva de los sistemas nucleares
  • Modelización de estructuras de espuma y celulares
  • Modelado de tejido morfogénesis

Otros métodos que emplean Monte Carlo

• Modelos al azar clasificadas, por ejemplo, criticidad autoorganizada
• Simulación directa Monte Carlo
• Dinámica método de Monte Carlo
• Kinetic Monte Carlo
• Quantum Monte Carlo
• Método Carlo Monte-Quasi usando secuencias de baja discrepancia y paseos auto evitando
• Transporte de carga Semiconductor y similares
• Microscopía electrónica interacciones haz de la muestra
• Optimización estocástica
• Modelo celular Potts
• Cadena de Markov Monte Carlo
• Cross-Entropy Método
• Economía Aplicada información

Utilice en matemáticas

En general, los métodos de Monte Carlo se utilizan en las matemáticas para resolver diversos problemas mediante la generación de números aleatorios adecuados y la observación de que la fracción de los números que obedecen a alguna propiedad o propiedades. El método es útil para obtener soluciones numéricas a problemas que son demasiado complicados de resolver analíticamente. La aplicación más común del método de Monte Carlo es la integración Monte Carlo.

Integración

Métodos deterministas de integración numérica operan mediante la adopción de un número de muestras uniformemente espaciados a partir de una función. En general, esto funciona muy bien para funciones de una variable. Sin embargo, para funciones de vectores , los métodos de cuadratura deterministas pueden ser muy ineficiente. Para integrar numéricamente una función de un vector de dos dimensiones, rejilla igualmente espaciados puntos sobre una superficie de dos dimensiones son obligatorios. Por ejemplo, una cuadrícula de 10x10 requiere 100 puntos. Si el vector tiene 100 dimensiones, la misma separación en la parrilla requeriría 10 ¹⁰⁰ puntos, demasiados para ser calculado. 100 dimensiones es de ninguna manera irrazonable, ya que en muchos problemas físicos, una "dimensión" es equivalente a un grado de libertad. (Ver La maldición de la dimensionalidad.)

Métodos de Monte Carlo proporcionan una manera de salir de este tiempo-exponencial aumento. Mientras la función en cuestión es razonablemente buen comportamiento, se puede estimar por la selección de puntos al azar en el espacio 100-dimensional, y teniendo algún tipo de promedio de los valores de la función en estos puntos. Por el ley de los grandes números, este método se mostrará 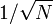convergencia, es decir cuadruplicar el número de puntos muestreados se reducir a la mitad el error, sin importar el número de dimensiones.

Un refinamiento de este método es hacer que de alguna manera los puntos al azar, pero es más probable que venir de regiones de alta contribución a la integral de las regiones de baja contribución. En otras palabras, los puntos deben ser extraídos de una distribución similar en la forma a que el integrando. Es comprensible que, haciendo esto, precisamente, es tan difícil como la solución de la integral en el primer lugar, pero hay métodos aproximados disponibles: desde simplemente que componen una función integrable cree que es similar, a una de las rutinas de adaptación discutidas en los temas que aparecen a continuación.

Un enfoque similar implica el uso de bajo discrepancia secuencias lugar-la método de Carlo-Monte cuasi. Métodos Carlo Monte-Cuasi a menudo puede ser más eficiente en la integración numérica debido a que la secuencia de "llena" la zona mejor en un sentido y muestras más de los puntos más importantes que pueden hacer que la simulación convergen a la solución deseada más rápidamente.

Métodos de integración

• Métodos de muestreo directos
  • Muestreo de importancia
  • El muestreo estratificado
  • Muestreo estratificado recursiva
  • Algoritmo VEGAS
• Paseo aleatorio Monte Carlo incluyendo Cadenas de Markov
  • Algoritmo de Metropolis-Hastings
• Muestreo de Gibbs

Optimización

Otra de las aplicaciones de gran alcance y muy popular para los números aleatorios en la simulación numérica es en optimización numérica. Estos problemas utilizan funciones de algunos vector a menudo grandes dimensiones que han de ser minimizado (o maximizado). Muchos problemas pueden formularse de esta manera: por ejemplo, un programa de ajedrez de ordenador podría ser visto como tratando de encontrar el conjunto óptimo de, digamos, 10 movimientos que produce la mejor función de evaluación al final. La problema del vendedor viajero es otro problema de optimización. También hay aplicaciones en el diseño de ingeniería, tales como la optimización del diseño multidisciplinar.

La mayoría de los métodos de optimización de Monte Carlo se basan en aleatoria camina. En esencia, el programa se moverá alrededor de un marcador en el espacio multidimensional, que tiende a moverse en direcciones que conducen a una función menor, pero a veces se mueve en contra de la gradiente.

Métodos de optimización

• Estrategia Evolución
• Los algoritmos genéticos
• Revenido Paralelo
• El recocido simulado
• Optimización estocástica
• Túnel estocástico

Los problemas inversos

Formulación probabilística de problemas inversos conduce a la definición de una distribución de probabilidad en el espacio modelo. Esta distribución de probabilidad cosechadoras información a priori con la nueva información obtenida mediante la medición de algunos parámetros observables (datos). Como, en el caso general, la teoría de la vinculación de los datos con los parámetros del modelo no es lineal, la probabilidad a posteriori en el espacio modelo no puede ser fácil de describir (puede ser multimodal, algunos momentos no se pueden definir, etc.).

Al analizar un problema inverso, la obtención de un modelo de probabilidad máxima es por lo general no es suficiente, ya que normalmente también desea tener información sobre el poder de resolución de los datos. En el caso general es posible que tengamos un gran número de parámetros del modelo, y una inspección de las densidades de probabilidad marginales de interés puede ser poco práctico, o incluso inútil. Pero es posible generar de forma pseudoaleatoria una gran colección de modelos de acuerdo a la distribución de probabilidad posterior y para analizar y visualizar los modelos de tal manera que la información sobre las probabilidades relativas de Características del modelo se transmite al espectador. Esto se puede lograr por medio de un método de Monte Carlo eficiente, incluso en los casos en que no se dispone de fórmula explícita para la distribución a priori.

El método de muestreo importancia más conocido, el algoritmo de Metropolis, se puede generalizar, y esto le da un método que permite el análisis de (posiblemente no lineales) problemas inversos con complejo de información a priori y datos con una distribución arbitraria de ruido. Para obtener más información, consulte Mosegaard y Tarantola (1995) O Tarantola (2005) .

Monte Carlo y números aleatorios

Curiosamente, los métodos de simulación de Monte Carlo por lo general no requieren de verdad números aleatorios sean útiles - para otras aplicaciones, tales como pruebas de primalidad, imprevisibilidad es vital (ver Davenport (1995)). Muchas de las técnicas más útiles utilizan determinista, secuencias pseudo-aleatorios, por lo que es fácil de probar y simulaciones volver a ejecutar. La única cualidad suele ser necesario reparar simulaciones es para la secuencia pseudo-aleatoria a aparecer "bastante aleatorio" en cierto sentido.

Lo que esto significa depende de la aplicación, pero por lo general debe pasar una serie de pruebas estadísticas. Pruebas de que los números son distribuido o seguir otra distribución deseada cuando un número suficientemente grande de elementos de la secuencia se consideran es uno de los más simples y más comunes de manera uniforme.

Una alternativa al método básico Monte Carlo

Economía de la información Aplicadas (AIE) es un método de análisis de decisión utilizado en los negocios y el gobierno que se ocupa de algunas de las debilidades del método de Monte Carlo - al menos la forma en que se emplea normalmente en situaciones prácticas. Los componentes más importantes AIE añade al método de Monte Carlo son:

1) Contabilidad para el exceso de confianza sistémica de estimadores humanos con El grado de probabilidad calibrada

2) Cálculo del valor económico de la información para guiar las mediciones empíricas adicionales

3) Con los resultados de Monte Carlos, como aporte a análisis de la cartera

Cuando se utilizan simulaciones de Monte Carlo en la mayoría de los ajustes de análisis de decisión, los expertos humanos se utilizan para estimar las probabilidades y los rangos en el modelo. Sin embargo, la investigación en psicología de decisiones en el campo de evaluaciones de probabilidad calibrados muestra que los humanos - especialmente los expertos en diversos campos - tienden a ser estadísticamente exceso de confianza. Es decir, que ponen demasiado alta la probabilidad de que se produzca un resultado previsto y tienden a usar rangos que son demasiado estrechas para reflejar su incertidumbre. AIE implica formación estimadores humanos por lo que las probabilidades y los rangos que proporcionan realista reflejan la incertidumbre (por ejemplo., Un intervalo de confianza del 90% subjetivo como un 90% de probabilidades de contener el valor verdadero). Sin este tipo de formación, los modelos de Monte Carlo invariablemente subestimar la incertidumbre de una decisión y por lo tanto el riesgo.

Otro defecto es que, en la práctica, la mayoría de los usuarios de simulaciones de Monte Carlo se basan totalmente en las estimaciones subjetivas iniciales y casi nunca seguimiento con la observación empírica. Esto puede ser debido a la gran cantidad de variables en muchos modelos y la incapacidad de los analistas para elegir las variables económicamente justificadas para medir más. AIE aborda esta usando métodos de teoría de la decisión para calcular el valor económico de la información adicional. Esto generalmente elimina la necesidad de medir la mayoría de las variables y pone restricciones pragmáticas sobre los métodos utilizados para medir las variables que tienen un valor de información significativa.

La última deficiencia abordado por AIE es que la salida de un Monte Carlo - por lo menos para el análisis de las decisiones de negocios - es simplemente el histograma de los rendimientos resultantes. No se presenta criterios para determinar si una distribución particular de los resultados es aceptable o no. Usos AIE Teoría Moderna del Portafolio para determinar qué inversiones son deseables y cuáles son sus prioridades relativas deberían ser.