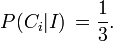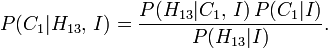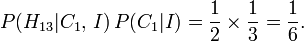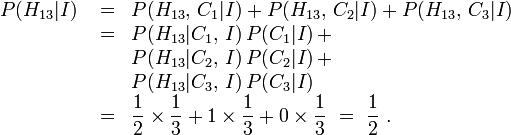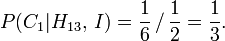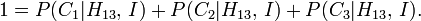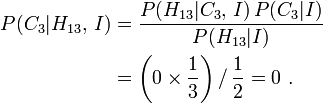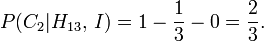Problema de Monty Hall
Antecedentes de las escuelas de Wikipedia
Los artículos de esta selección escuelas se han organizado por tema currículo gracias a voluntarios SOS. El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.
El problema de Monty Hall es un rompecabezas que implica la probabilidad basada libremente en el programa de juegos de América Vamos a hacer un trato. El nombre proviene de la conductora del programa, Monty Hall. El problema también se conoce como la paradoja de Monty Hall; es un paradoja verídica en el sentido de que la solución es contrario a la intuición.
Una declaración ampliamente conocida del problema apareció en una carta a Columna de Marilyn Pregunta de Marilyn vos Savant en Desfile:
Supongamos que estás en un programa de juegos, y ya está dada la opción de tres puertas: Detrás de una puerta es un coche; detrás de los otros, cabras. Usted escoge una puerta, dices No. 1, y el anfitrión, que sabe lo que hay detrás de las puertas, se abre otra puerta, dices No. 3, que tiene una cabra. A continuación, te dice: "¿Quieres recoger puerta Nº 2?" Es a su ventaja para cambiar su elección? (Whitaker 1990)
Porque no hay manera para que el jugador sabe cuál de las dos puertas sin abrir es la puerta de ganar, casi todas las personas asumir que cada puerta tiene la misma probabilidad y concluir que el cambio no importa. De hecho, en la interpretación usual del problema el jugador debe cambiar-hacerlo duplica la probabilidad de ganar el coche desde 01/03 hasta 02/03.
Cuando el problema y la solución apareció en el desfile, aproximadamente 10.000 lectores, entre ellos varios cientos de profesores de matemáticas, escribió a la revista reclamando la solución publicada fue mal. Parte de la controversia era porque la declaración Desfile del problema no especifica completamente el comportamiento del huésped y por lo tanto técnicamente ambigua. Sin embargo, incluso cuando se administra declaraciones totalmente inequívocos de problemas, explicaciones, simulaciones y pruebas matemáticas formales, muchas personas aún se encuentran la respuesta correcta con incredulidad.
Problema
Steve Selvin escribió una carta al Estadístico de América en 1975 que describe un problema vagamente basado en el programa de juegos Hagamos un Trato (1975a Selvin). En una carta posterior que llamó este problema el "problema de Monty Hall" (1975b Selvin). El problema es matemáticamente equivalente (Morgan et al., 1992) a la Tres presos problema descrito en La columna de juegos matemáticos de Martin Gardner en Scientific American en 1959 (Gardner 1959). El problema de Monty Hall se actualizó, citado anteriormente, en una carta de 1990 a Columna de Marilyn Pregunta de Marilyn vos Savant en Parade (Whitaker, 1990).
La declaración del problema en la columna Pregunte Marilyn en desfile deja aspectos críticos de la conducta del anfitrión no declarado, por lo que el problema matemáticamente ambigua (Mueser y Granberg 1999). El análisis estándar del problema también asume que el anfitrión está obligado a abrir siempre una puerta revelando una cabra, que siempre hacer la oferta para cambiar, y para abrir uno de los restantes dos puertas al azar si el jugador inicialmente recogió el coche (Barbeau 2000 ,. p 87). Una declaración matemáticamente explícita del problema es:
Suponga que usted está en un programa de juegos y se te da la opción de tres puertas. Detrás de una puerta es un coche; detrás de los otros, cabras. El coche y las cabras fueron colocados al azar detrás de las puertas antes del show. Las reglas del concurso son las siguientes: Después de haber seleccionado una puerta, la puerta permanece cerrada por el momento. El presentador de televisión, Monty Hall, que sabe lo que hay detrás de las puertas, ahora tiene que abrir una de las dos puertas restantes, y la puerta se abre debe tener una cabra detrás de él. Si los dos restantes puertas tienen cabras detrás de ellos, se elige uno al azar. Después de Monty Hall abre una puerta con una cabra, se le pedirá que decidir si quiere quedarse con su primera elección o para cambiar a la última puerta restante. Imagínese que usted eligió la puerta 1 y se abre el anfitrión Puerta 3, que tiene una cabra. A continuación, le pregunta "¿Quieres cambiar a la puerta número 2?" ¿Es una ventaja para cambiar su elección? (Krauss y Wang 2003, p. 10)
El jugador inicialmente puede elegir cualquiera de las tres puertas, no sólo de la puerta 1, y luego el anfitrión abre una puerta diferente revelando una cabra, no necesariamente de la puerta 3, y da al jugador una segunda elección entre los dos restantes puertas sin abrir.
Solución
La posibilidad de elegir inicialmente el coche es uno de cada tres, que es la oportunidad de ganar, el coche por pegar con esta elección. Por el contrario, la posibilidad de elegir inicialmente una puerta con una cabra es dos de cada tres, y un reproductor originalmente elegir una puerta con una cabra victorias por conmutación. En ambos casos, el anfitrión debe revelar una cabra. En el caso 2.3, donde el jugador elige inicialmente una cabra, el anfitrión debe revelar la otra cabra haciendo la única puerta que queda el uno con el coche.
| |||||||||||||||||||||||||||
El jugador tiene la misma oportunidad de seleccionar inicialmente el coche, Cabra A o B. Cabra conmutación resulta en un ganar 2/3 del tiempo debido a 2/3 del tiempo, selección inicial del jugador era una cabra. | |||||||||||||||||||||||||||
Como se muestra en el diagrama de arriba, hay tres situaciones posibles correspondientes a la elección inicial del jugador, cada uno con una probabilidad de 1/3:
- El jugador originalmente escogió la puerta que oculta el coche. El anfitrión juego ha mostrado uno de los dos machos cabríos.
- El jugador originalmente tomó la puerta ocultando cabra A. El anfitrión juego ha mostrado la otra cabra.
- El jugador originalmente tomó la puerta ocultando Cabra B. El anfitrión juego ha mostrado la otra cabra.
Si el jugador opta por cambiar, el coche se va a ganar en cualquiera de los dos últimos casos. Un jugador la elección de quedarse con la elección inicial gana en sólo el primer caso. Dado que en dos de cada tres casos igualmente probables conmutación victorias, la probabilidad de ganar por conmutación es 2/3. En otras palabras, los jugadores que cambian ganarán el coche en promedio dos veces de cada tres.
El razonamiento anterior se aplica a todos los jugadores en medio sin tener en cuenta que la puerta específica abre el anfitrión y todos los jugadores individuales en el comienzo del juego, pero no a un jugador específico en el punto al jugador se le pregunta si va a cambiar dado que la puerta del anfitrión tiene abierto (Morgan et al. 1991). Esta diferencia es sutil, pero dependiendo de la formulación exacta del problema puede afectar el resultado (ver Otras conductas de acogida , más adelante). La determinación de la probabilidad condicional de ganar por conmutación dado que la puerta se abre de acogida exige un análisis diferente.
Un oficial análisis bayesiano muestra la probabilidad de ganar el coche al cambiar dado el anfitrión abre la puerta 3 es 2/3, ver el análisis bayesiano continuación.
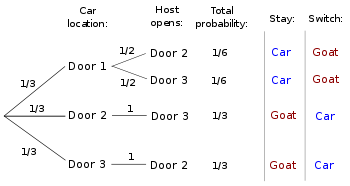
La árbol de decisión se puede usar para determinar tanto la probabilidad global de ganar por la conmutación y la probabilidad condicional dado que la puerta se abre host (Grinstead y Snell 2006, p. 137-138). Suponiendo que el enunciado del problema dado anteriormente y que el jugador inicialmente recoge Puerta 1, el árbol muestra que gana de conmutación en los dos casos en los que el jugador no inicialmente recoger el coche, con una probabilidad total combinado de 02.03. Esta es la probabilidad de ganar, por el cambio. El árbol también muestra que sólo hay dos posibles condiciones en las que el anfitrión abre la puerta 2, y que la conmutación pierde en el caso 1/6 donde el coche está detrás de la puerta 1 y gana en el caso 1/3 donde el coche está detrás de la puerta 3. Del mismo modo, si el anfitrión abre la puerta 3, el árbol muestra conmutación pierde en el caso 01/06, donde el coche está detrás de la puerta 1 y gana en el caso 1/3 donde el coche está detrás de la puerta 2. Cambio gana dos veces más que quedando independientemente de qué puerta se abre el anfitrión, por lo que la probabilidad condicional de ganar cambiando dado ya sea puerta se abre el anfitrión es la misma que la probabilidad global - ambos son 2/3.
Ayudas a la comprensión
¿Por qué la probabilidad es 2/3
La objeción más comúnmente expresado que la solución es que el pasado puede ser ignorada al evaluar la probabilidad de que es irrelevante que las puertas al jugador inicialmente recoge y se abre el anfitrión. Sin embargo, en el problema que se presenta en un principio, la elección inicial del jugador hace influir en las opciones disponibles del huésped posteriormente.
Esta diferencia se puede demostrar contrastando el problema original con una variación que apareció en la columna de vos Savant en noviembre de 2006. En esta versión, se olvida de que la puerta de Monty Hall oculta el coche. Se abre una de las puertas al azar y se alivia cuando una cabra se revela. Cuando se le preguntó si el concursante debe cambiar, vos Savant respondido correctamente, "Si el host no tiene ni idea, que no hace ninguna diferencia si te quedas o interruptor. Si él sabe, interruptor" (vos Savant, 2006).
En esta versión del puzzle, el jugador tiene la misma oportunidad de ganar si el cambio o no. Hay seis posibles secuencias de eventos que pueden ocurrir, cada uno con una probabilidad de 1/6:
Selecciones del jugador Host revela Tercera puerta contiene Cabra A Coche Cabra B Cabra B Coche Cabra A Cabra A Cabra B Coche Cabra B Cabra A Coche Coche Cabra A Cabra B Coche Cabra B Cabra A
En los dos primeros casos anteriores, el anfitrión revela el coche. ¿Qué podría suceder en estos casos es desconocida, tal vez el concursante inmediatamente gana o pierde inmediatamente. Sin embargo, en el problema como se ha dicho, la acogida ha revelado una cabra, por lo que sólo cuatro de los seis casos sigue siendo posible, y son igualmente probables. En dos de estos cuatro casos, el cambio de los resultados en la victoria, y en los otros dos, de conmutación resultados en una cabra. Siguiendo con el original de la selección da las mismas posibilidades: una pérdida en dos casos y una victoria en otros dos.
Probabilidad de que el jugador de ganar cambiando aumenta a 3.2 en el problema según lo declarado por Mueser y Granberg porque en los dos casos anteriores donde el anfitrión revelaría el coche, se ve obligado a revelar la cabra que queda en su lugar. En la tabla a continuación, selecciones del huésped de la tabla anterior se resaltan. Debido a que no puede revelar el coche, su comportamiento se altera en dos casos:
Selecciones del jugador Host revela Tercera puerta contiene Cabra A Cabra B Coche Cabra B Cabra A Coche Cabra A Cabra B Coche Cabra B Cabra A Coche Coche Cabra A Cabra B Coche Cabra B Cabra A
Este cambio en el comportamiento del huésped hace que el coche sea el doble de probabilidades de estar detrás de la "tercera puerta", y es lo que causa el cambio a ser el doble de probabilidades de ganar en el "host sabe" variación del problema.
Aumentar el número de puertas
Puede ser más fácil de apreciar la solución considerando el mismo problema con 1.000.000 puertas en lugar de sólo tres (vos Savant 1990). En este caso hay 999.999 puertas con cabras detrás de ellos y una puerta con un premio. El jugador escoge una puerta. El anfitrión del juego se abre 999,998 de las otras puertas que revelan 999.998 cabras - imagínese el anfitrión empezando por la primera puerta y bajando una línea de 1.000.000 puertas, apertura de cada uno, pasando por alto la única puerta del jugador y otra puerta. El anfitrión entonces ofrece al jugador la oportunidad de cambiar a la única otra puerta sin abrir. En promedio, en 999.999 fuera de 1.000.000 veces la otra puerta contendrá el premio, ya que 999.999 de 1.000.000 de veces que el jugador tomó por primera vez una puerta con una cabra. Un jugador racional debe cambiar.
Diagrama de Venn
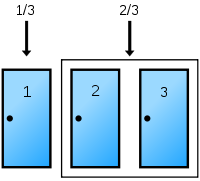
La probabilidad media de ganar el coche por el cambio puede ilustrarse utilizando diagramas de Venn . Después de elegir la puerta 1, por ejemplo, el jugador tiene la oportunidad de 1/3 de haber seleccionado la puerta con el coche, dejando una probabilidad 2/3 entre las otras dos puertas, como se muestra a continuación. Tenga en cuenta que hay un 100% de probabilidad de encontrar una cabra detrás de al menos una de las dos puertas no elegidas, porque sólo hay un coche.
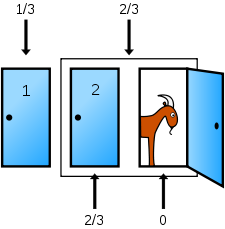
El anfitrión abre ahora la puerta 3. En las condiciones de la declaración del problema se requiere el host para abrir una de las otras dos puertas, y la misma probabilidad de abrir cualquiera de las puertas no elegido; abrir esta puerta no afecta la probabilidad de ganar el coche por quedarse con la opción original, que sigue siendo un tercio. Todavía hay una probabilidad de 2/3 de que el coche está detrás de cualquier puerta 2 o Puerta 3. Sin embargo, ya que el coche no está detrás de la puerta 3, sabemos que estar detrás de una de estas puertas significa que el coche está detrás de la puerta 2; por lo tanto, que 2/3 de probabilidad es ahora una probabilidad de que el coche está detrás de la puerta 2, como se muestra a continuación. Otra forma de expresar esto es que si el coche está detrás de una de las puertas de 2 ó 3, con la apertura de la puerta 3 del anfitrión ha revelado que debe estar detrás de la puerta 2. (Devlin, 2003)
Combinando puertas
En vez de una puerta que se abre y se muestra como una puerta perdedora, una acción equivalente es combinar las dos puertas no elegidas en uno ya que el jugador no puede, y no, elegir la puerta abierta (Adams 1990; Devlin 2003; Williams 2004). Por consiguiente, el jugador tiene la opción de quedarse con la elección original de puerta con una probabilidad de 1/3 de ganar el coche, o la elección de la suma de los contenidos de las otras dos puertas con una probabilidad de 2/3. Los supuestos juego juegan un papel aquí conmutación es equivalente a tomar el contenido combinados si y sólo si se requiere el anfitrión del juego para abrir una puerta con una cabra y elige entre dos puertas de perder al azar con probabilidades iguales.
En este caso, lo que debe ser ignorado es la apertura de la puerta. El jugador realidad elige entre la puerta recogido originalmente y los otros dos uno -apertura es simplemente una distracción. La elección original divide las posibles ubicaciones del coche entre la puerta el jugador recoge con una probabilidad de 1/3 y los otros dos con una probabilidad de 2/3. Ya se sabe que al menos una de las dos puertas unpicked contiene una cabra. Revelando la cabra por lo tanto le da al jugador ninguna información adicional sobre la puerta elegida inicialmente; no cambia el 2/3 probabilidad de que el coche está todavía en el bloque de dos puertas.
Simulación
Una forma sencilla de demostrar que una estrategia de conmutación realmente ganar dos de tres veces en el medio es para simular el juego con naipes (Gardner 2001, Pág. 243). Tres cartas de una baraja ordinaria se utilizan para representar las tres puertas; una tarjeta "especial" como el as de espadas debe representar la puerta con el coche, y las tarjetas ordinarias, como los dos grupos de dos rojos, representar las puertas de cabra.
La simulación, usando el siguiente procedimiento, se puede repetir varias veces para simular múltiples rondas del juego. Una carta se reparte al azar para el "jugador", para representar a la puerta del jugador escoge inicialmente. Luego, mirando a las dos cartas restantes al menos uno de los cuales debe ser un dos rojos, el "anfitrión" descarta una dos rojas. Si la tarjeta queda en la mano del anfitrión es el as de espadas, esto se registra como una ronda donde el jugador habría ganado por el cambio; si el anfitrión es la celebración de dos de color rojo, la ronda se registra como una en la estancia habría ganado.
Por el ley de los grandes números, este experimento es probable que aproximar la probabilidad de ganar, y ejecutar el experimento durante bastantes rondas no sólo debe verificar que el jugador no gana al cambiar dos veces de tres, pero muestra por qué. Dos de cada tres veces, después de una tarjeta se ha tratado al jugador, el as de espadas está en la mano del anfitrión. En ese momento, ya se determina si quedarse o conmutación ganará la ronda para el jugador.
Si este no es convincente, la simulación se puede hacer con toda la cubierta, que trata de una tarjeta al jugador y manteniendo la otra 51 (Adams 1990). En esta variante, el as de espadas va al anfitrión 51 veces de cada 52, y se queda con el anfitrión, no importa cuántas cartas se descartan no -Ace.
Variantes
Otras conductas de acogida
En algunas versiones del problema de Monty Hall, no se especifica totalmente el comportamiento del huésped. Por ejemplo, la versión publicada en el desfile en 1990 no indicó específicamente que el anfitrión siempre abriría otra puerta, o siempre ofrecen una opción para cambiar, o incluso nunca abrir la puerta revelando el coche. Sin especificar estas reglas, el jugador no tiene suficiente información para concluir que el cambio va a ser exitosas dos terceras partes del tiempo (Mueser y Granberg, 1999). La tabla muestra las posibles conductas de acogida y el impacto en el éxito de la conmutación.
| Posibles conductas de acogida en un problema no especificado | |
|---|---|
| Comportamiento Host | Resultado |
| El anfitrión ofrece la opción de cambiar sólo cuando la elección inicial del jugador es la puerta de ganar (Tierney 2001). | El cambio siempre produce una cabra. |
| El anfitrión ofrece la opción de cambiar sólo cuando el jugador ha elegido de forma incorrecta (vos Savant 1996, p. 185). | El cambio siempre gana el coche. |
| El anfitrión no sabe lo que se esconde detrás de las puertas, y se abre una al azar, sin revelar el coche (vos Savant 1996, p. 181). | Conmutación gana el medio coche de la época. |
| El anfitrión abre una puerta conocida con probabilidad p, a menos que el coche está detrás de él (Morgan et al. 1991). | Si el anfitrión abre la puerta de su "habitual", el cambio de victorias con una probabilidad de 1 / (1+ p). Si el anfitrión abre la otra puerta restante, el cambio victorias con probabilidad p / (1 + p). |
| El anfitrión actúa como se indica en la versión específica del problema. | Conmutación gana el coche dos tercios del tiempo. |
Puertas secuenciales
No es una generalización del problema original de n puertas. En el primer paso, el jugador elige una puerta. El anfitrión juego entonces se abre otra puerta que es un perdedor. Si se desea, el jugador puede entonces cambiar a otra puerta. El anfitrión juego entonces se abre otra puerta perdedora, que aún no cerrado, diferente de elección actual del jugador. Entonces, el jugador puede cambiar de nuevo, y así sucesivamente. Esto continúa hasta que sólo hay dos puertas sin abrir izquierdo: Elección actual del jugador y otro. ¿Cuántas veces debe el interruptor de jugador, y cuando, en todo caso?
Una posible estrategia es seguir con la primera opción en todos los sentidos, pero luego cambiar al final. Con cuatro puertas, esta estrategia puede ser probada óptima; se ha afirmado que con n puertas, esta estrategia también es óptima y da una probabilidad de ganar igual a (n-1) / n (Bapeswara Rao y Rao 1992).
Este problema es similar al programa de televisión Deal or No Deal, que por lo general comienza con 26 cajas. El jugador selecciona uno a guardar, y luego escoge aleatoriamente cajas para abrir desde entre el resto. En este juego, incluso hasta el final, el cuadro de el jugador selecciona inicialmente y todos los cuadros de la izquierda no revelado tienen la misma probabilidad de ser el ganador. La distinción es que cualquier caja del jugador escoge para abrir podría revelar el gran premio, eliminando de esta manera que de la contienda. Monty en el otro lado, conoce los contenidos y está prohibido de revelar el ganador. Debido a que el Deal or No Deal es igual de probable que se abra el cuadro de ganar como de perder uno, la ventaja de Monty Hall se pierde. Suponiendo que el gran premio se sigue a la izquierda con dos cajas restantes, el jugador tiene una posibilidad de 50/50 de que la casilla seleccionada inicialmente contiene el gran premio.
Versión Quantum
Una versión cuántica de la paradoja ilustra algunos puntos acerca de la relación entre la información clásica o no cuántica y información cuántica, como codificado en los estados de los sistemas mecánicos cuánticos. La formulación se basa libremente en La teoría de juegos Quantum. Las tres puertas son reemplazados por un sistema cuántico que permite tres alternativas; abrir una puerta y mirando detrás de ella se traduce como hacer una medición en particular. Las reglas se pueden establecer en este idioma, y una vez más la opción para el jugador es seguir con la elección inicial, o cambiar a otra opción "ortogonal". La última estrategia resulta de duplicar las posibilidades, igual que en el caso clásico. Sin embargo, si el presentador no ha azar la posición del premio de una manera mecánica totalmente cuántica, el jugador puede hacerlo aún mejor, ya veces incluso puede ganar el premio con certeza (D'Ariano et al. 2002).
Historia del problema
Un problema esencialmente idéntica apareció como el Tres presos de problemas en La columna de juegos matemáticos de Martin Gardner en Scientific American en 1959 (Gardner 1959). Versión de Gardner hace que el procedimiento de selección explícito, evitando los supuestos no declarados en la versión desfile. Este rompecabezas en teoría de la probabilidad implica tres prisioneros, al azar de los que se ha elegido en secreto para ser ejecutado en la mañana. El primer preso pide al guardia que le dijera cuál de los otros dos saldrán bien librados, argumentando que este no revela ninguna información sobre si el preso será la víctima; el guardia responde afirmando que si el prisionero sabe que un determinado uno de los otros dos presos que queden libres se elevará probabilidad subjetiva del primer prisionero de ser ejecutado de 1/3 a 1/2. La pregunta es si el análisis del preso o el guardia es correcta. En la versión dada por Martin Gardner, el guardia a continuación, realiza un procedimiento de aleatorización particular para seleccionar qué nombre darle al preso; esto da el equivalente del problema de Monty Hall sin las ambigüedades habituales en su presentación.
En 1975, Steve Selvin escribió un par de cartas a la Americana de Estadística (1975a Selvin, Selvin 1975b) sobre el problema de Monty Hall. El primero presentó el problema en una versión próxima a su forma más popular; la versión presentada en el desfile 15 años después es la reproducción de la versión de Selvin. La segunda letra parece ser la primera utilización del término "problema de Monty Hall". El problema es en realidad una extrapolación de la demostración del juego. Monty Hall hizo abrir una puerta equivocada de crear entusiasmo, pero ofreció un menos conocido premio tales como $ 100 en efectivo en lugar de la opción de cambiar las puertas. Como Monty Hall escribió a Selvin:
Y si alguna vez tienes en mi programa, las reglas se aferran para ti, no hay cajas de negociación después de la selección. (Hall 1975)
El artículo de Phillip Martin en una edición 1989 de la revista Puente Hoy titulado "La trampa de Monty Hall" (Martin 1989) presentó el problema de Selvin, con la solución correcta, como un ejemplo de cómo se puede caer en la trampa de tratar la información no aleatoria, como si fuera aleatorio. Martin continuación se dan ejemplos en el juego de puente donde los jugadores comúnmente calculan mal las probabilidades de caer en la misma trampa, como el Principio de Restringido Choice. Dada la controversia que surja sobre este problema un año más tarde, Martin mostró una falta de presciencia cuando afirmó: "Aquí [en el problema de Monty Hall] la trampa es fácil de detectar. Pero la trampa puede surgir más sutilmente en un puente ajuste ".
Una versión refundido del planteamiento del problema de Selvin apareció en Pregunte Marilyn columna de Marilyn vos Savant de preguntas y respuesta de desfile en septiembre de 1990 (vos Savant 1990). Aunque vos Savant dio la respuesta correcta que el cambio iba a ganar dos tercios del tiempo, vos Savant estima 10.000 lectores, incluyendo varios cientos de matemáticas profesores escribieron en declarar que su solución era equivocada. Como resultado de la publicidad que el problema se ganó el nombre alternativo Marilyn y las cabras.
En noviembre de 1990, un debate igualmente polémico del artículo de vos Savant tuvo lugar en Columna de Cecil Adams The Straight Dope (Adams 1990). Adams respondieron inicialmente, incorrectamente, que las posibilidades de las dos puertas restantes deben ser cada uno en dos. Después de un lector escribió para corregir las matemáticas de análisis de Adams, Adams acordó que matemáticamente, que se había equivocado, pero dijo que la versión desfile dejó limitaciones críticas no declarada, y sin esas limitaciones, las posibilidades de ganar por el cambio no fuera necesariamente 2 / 3. Numerosos lectores, sin embargo, escribió en afirmar que Adams había sido "bien a la primera", y que las probabilidades correctas que uno de cada dos.
La columna Parade y su respuesta recibieron una considerable atención en la prensa, incluyendo un artículo de primera plana en el New York Times (Tierney 1991) en el que se entrevistó a sí mismo Monty Hall. Se apareció a entender el problema bastante bien, dando al reportero un demo con las llaves del coche y explicando cómo el juego real en Hagamos un Trato difería de las reglas del rompecabezas.
Más de 40 trabajos se han publicado sobre este problema en revistas académicas y la prensa popular (Mueser y Granberg 1999).
El problema sigue resurgir fuera de la academia. El sindicado Programa de NPR Charlas de autos aparece como uno de sus semanales "puzzles", y la respuesta que ofrecieron fue claramente explicada como la correcta (Magliozzi y Magliozzi, 1998). Una cuenta de matemático El primer encuentro de Paul Erdos del problema puede encontrarse en El hombre que amaba Sólo Números -al igual que muchos otros, que inicialmente se equivocó. Se discute el problema, desde la perspectiva de un niño con síndrome de Asperger , en El curioso incidente del perro a medianoche nocturna , una novela de 2003 por Mark Haddon. El problema también se aborda en una conferencia del personaje Charlie Eppes en un episodio del drama de la CBS NUMB3RS (Episodio 1.13) y en 2.006 libros Trucos de la mente de Derren Brown. El problema de Monty Hall (aunque se le llamó "la demostración del juego problema host" en la película) aparece en la película 21, en la que el personaje principal, Ben, responde correctamente a la pregunta en su curso de matemáticas de la universidad MIT. Economista M. Keith Chen identificó un defecto potencial en cientos de experimentos relacionados con disonancia cognitiva que utilizan un análisis con problemas similares a los involucrados en el problema de Monty Hall (Tierney 2008).
Análisis bayesiano
Un análisis del problema utilizando el formalismo de Teoría de la probabilidad bayesiana (Gill 2002) hace explícito el papel de los supuestos subyacentes del problema. En términos bayesianos, las probabilidades están asociadas a las proposiciones, y expresan un grado de creencia en su verdad, sin perjuicio de cualquier fondo la información que pasa a ser conocido. Para este problema de fondo es el conjunto de reglas de juego, y las proposiciones de interés son:
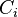 : El coche está detrás de la puerta i, para i igual a 1, 2 o 3.
: El coche está detrás de la puerta i, para i igual a 1, 2 o 3.
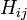 : El anfitrión abre la puerta j después de que el jugador se ha recuperado de la puerta i, para i y j igual a 1, 2 o 3.
: El anfitrión abre la puerta j después de que el jugador se ha recuperado de la puerta i, para i y j igual a 1, 2 o 3.
Por ejemplo, 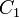 denota la proposición el coche está detrás de la puerta 1, y
denota la proposición el coche está detrás de la puerta 1, y 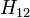 denota la proposición el anfitrión abre la puerta 2 después de que el jugador se ha recuperado de la puerta 1. Indicando la información de fondo con
denota la proposición el anfitrión abre la puerta 2 después de que el jugador se ha recuperado de la puerta 1. Indicando la información de fondo con 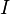 , Los supuestos se determinan formalmente de la siguiente manera.
, Los supuestos se determinan formalmente de la siguiente manera.
En primer lugar, el coche puede estar detrás de cualquier puerta, y todas las puertas son a priori la misma probabilidad de ocultar el coche. En este contexto significa a priori antes de que el juego se juega, o antes de ver a la cabra. Por lo tanto, la probabilidad a priori de una proposición 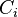 es:
es:
En segundo lugar, el anfitrión siempre se abrirá una puerta que no tiene coche detrás de él, escogido entre los dos no escogido por el jugador. Si dos de esas puertas están disponibles, es igualmente probable que se abra cada uno. Esta norma determina la probabilidad condicional de una proposición 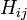 sujeto a que el coche es - es decir, a condición de una proposición
sujeto a que el coche es - es decir, a condición de una proposición 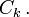 Específicamente, es:
Específicamente, es:
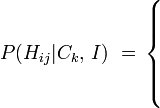
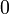
si i = j, (el anfitrión no puede abrir la puerta escogido por el jugador) 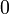
si j = k, (el anfitrión no puede abrir una puerta con un coche detrás de él) 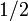
si i = k, (las dos puertas con ningún coche son igualmente probable que se abra) 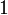
si yo 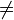 k y j
k y j 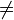 k, (sólo hay una puerta disponible para abrir)
k, (sólo hay una puerta disponible para abrir)
El problema ahora puede ser resuelto por puntuación de cada estrategia con su asociado posterior de probabilidad de ganar, que está con su probabilidad sujetos a la apertura del anfitrión de una de las puertas. Sin pérdida de generalidad, se supone, por la re-numeración de las puertas si es necesario, que el jugador toma la puerta 1, y que el anfitrión se abre la puerta 3, revelando una cabra. En otras palabras, el anfitrión hace proposición 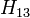 cierto.
cierto.
La parte posterior de probabilidad de ganar por no cambiar las puertas, con sujeción a las reglas del juego y 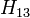 , Es entonces
, Es entonces 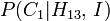 . Uso El teorema de Bayes esto se expresa como:
. Uso El teorema de Bayes esto se expresa como:
Por los supuestos mencionados anteriormente, el numerador de la parte derecha es:
La constante de normalización en el denominador se puede evaluar mediante la ampliación utilizando las definiciones de probabilidad marginal y probabilidad condicional:
Dividiendo el numerador por los rendimientos constantes normalizadoras:
Tenga en cuenta que esto es igual a la probabilidad a priori del ser del coche detrás de la puerta elegida inicialmente, lo que significa que la acción del anfitrión no ha aportado ninguna información nueva con respecto a esta eventualidad. De hecho, el argumento siguiente muestra que el efecto de la acción del anfitrión se compone enteramente de la redistribución de las probabilidades de ser del coche detrás de cualquiera de las otras dos puertas.
La probabilidad de ganar al cambiar la selección a la puerta 2, 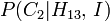 , Se puede evaluar al exigir que las probabilidades a posteriori de toda la
, Se puede evaluar al exigir que las probabilidades a posteriori de toda la 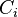 proposiciones se suman a 1. Es decir:
proposiciones se suman a 1. Es decir:
No hay coche detrás de la puerta 3, ya que el anfitrión abrió, por lo que el último término debe ser cero. Esto se puede comprobar mediante el teorema de Bayes y los resultados anteriores:
Por lo tanto:
Esto demuestra que la estrategia ganadora es para cambiar la selección a puerta 2. También deja claro que muestra de la serie de la cabra detrás de la puerta 3 tiene el efecto de transferir el 1/3 de probabilidad de ganar a priori asociado con esa puerta a la restante no seleccionada y sin abrir, por lo que es la opción más probable ganador.