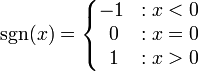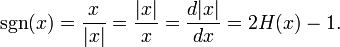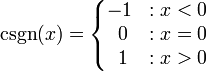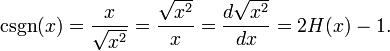Número negativo
Antecedentes
SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...
Un número negativo es un número que es menos de cero , tal como -3. Un número positivo es un número que es mayor que cero, como 3. Cero en sí no es ni positivo ni negativo. Los números no negativos son los números reales que no son negativos (son positivos o cero). Los números no son positivos los números reales que no son positivas (que son negativos o cero).
En el contexto de los números complejos , implica positivo real, pero para mayor claridad se puede decir "número real positivo".
Los números negativos
Enteros negativos puede ser considerado como una extensión de los números naturales , de manera que la ecuación x - y = z tiene una solución significativa para todos los valores de x e y. Los otros conjuntos de números se derivan como extensiones progresivamente más elaboradas y generalizaciones a partir de los números enteros.
Los números negativos son útiles para describir los valores en una escala que va por debajo de cero, tales como la temperatura , y también en teneduría de libros, donde pueden ser usados para representar deudas. En la contabilidad, las deudas son a menudo representados por números rojos, o un número entre paréntesis.
Números no negativos
Un número es no negativo si y sólo si es mayor que o igual a cero , es decir, positivo o cero. Así, los números enteros no negativos son todos los enteros desde cero en alza, y los reales no negativos son todos los números reales a partir de cero en alza.
Una verdadera matriz A se llama no negativo si cada entrada de A es no negativo.
Una verdadera matriz A se llama totalmente negativo por los teóricos de la matriz o totalmente positiva por científicos de la computación si el determinante de cada submatriz cuadrada de A es no negativo.
El negativo de un número es único
La negativa de un número es único, como lo muestra la siguiente prueba.
La prueba está en contradicción.
Sea x un número y vamos -x ser su negativo. Dejar 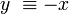 . Dejar
. Dejar 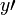 ser otro negativo de x. Entonces debe ser cierto que
ser otro negativo de x. Entonces debe ser cierto que 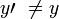 . Por un axioma del sistema de números reales
. Por un axioma del sistema de números reales
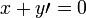 ,
, 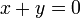 .
.
Y así, 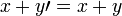 . Usando la ley de cancelación para Además, se ve que
. Usando la ley de cancelación para Además, se ve que 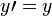 , Lo que contradice nuestra suposición. Por lo tanto
, Lo que contradice nuestra suposición. Por lo tanto 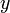 es el mismo número que
es el mismo número que 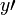 y es el negativo única de x.
y es el negativo única de x.
Función signo
Es posible definir una función sgn (x) sobre los números reales que es 1 para los números positivos, -1 para los números negativos y 0 para el cero (a veces llamado el función signo):
Tenemos entonces (excepto para x = 0):
Donde | x | es el valor absoluto de x y H (x) es la Función escalón de Heaviside. Ver también derivado .
Función signo Complex
Es posible definir un CSGN función (x) sobre los números complejos, que es 1 para los números positivos, -1 para los números negativos y 0 para el cero (a veces llamado el función signo complejo):
Cuando el complejo de la desigualdad debe ser interpretada como sigue
Tenemos entonces (excepto para x = 0):
Aritmética involucrando números con signo
Suma y resta
A los efectos de suma y resta, se puede pensar en los números negativos como deudas.
Adición de un número negativo es el mismo que restar el número positivo correspondiente:
- 5 + (-3) = 5 - 3 = 2
- (Si usted tiene $ 5 y adquirir una deuda de $ 3, entonces usted tiene un patrimonio neto de $ 2)
- -2 + (-5) = -2-5 = -7
(Con el fin de evitar la confusión entre los conceptos de la resta y la negación, a menudo el signo negativo se escribe como un exponente:
- - 2 + - 5 = - 2-5 = - 7)
Restar un número positivo de un número positivo menor produce un resultado negativo:
- 4 - 6 = -2
- (Si usted tiene $ 4 y $ 6 pasa entonces usted tiene una deuda de $ 2).
Restar un número positivo de cualquier número negativo se obtiene un resultado negativo:
- -3-6 = -9
- (Si tiene una deuda de $ 3 y gastar otros $ 6, usted tiene una deuda de $ 9).
Restando un negativo equivale a añadir la correspondiente positivo:
- 5 - (-2) = 5 + 2 = 7
- (Si tiene un patrimonio neto de $ 5 y deshacerse de una deuda de $ 2, a continuación, su nuevo valor neto es de $ 7).
También:
- -8 - (-3) = -5
- (Si tiene una deuda de $ 8 y deshacerse de una deuda de $ 3, entonces usted todavía tiene una deuda de $ 5).
Multiplicación
Brahmagupta declaró en Brahmasputhasiddhanta "tiempos positivos positivo es momentos positivos y negativos negativo es positivo". Esta noción fue desafiado por Lazare Carnot (1753-1823). Me preguntó cómo podía el cuadrado de un número menor será más grande que el cuadrado de un número grande. En otras palabras cuadrado de -3 es mayor que el cuadrado de 2. Sin embargo, -3 es menor que 2. Esta objeción de Carnot a la noción de Brahmagupta se puso indiscutible durante un siglo. Grandes matemáticos como Euler, Laplace y Cauchy fueron incapaces de dar una respuesta completa. Hermann Hankel probó el uso de números complejos que Brahmagupta tenía razón. . (Referencia intuición en Ciencias y Matemáticas, Efraín Fischbein, Kluwer Academic Publishers, Springer, 1899) Multiplicación de un número negativo por un número positivo se obtiene un resultado negativo: -2 × 3 = -6. La multiplicación de dos números negativos se obtiene un resultado positivo: -4 × -3 = 12.
Una manera de entender esto es considerar la multiplicación por un número positivo como suma repetida. Piense en 3 x 2 como 3 grupos, con 2 en cada grupo. Por lo tanto, 3 × 2 = 2 + 2 + 2 = 6 y así naturalmente -2 × 3 = (-2) + (-2) + (-2) = -6.
La multiplicación por un número negativo puede considerarse como adición repetida también. Por ejemplo, 3 × -2 puede ser pensado como 3 grupos, con -2 en cada grupo. 3 × -2 = (-2) + (-2) + (-2) = -6. Tenga en cuenta que esto mantiene la multiplicación conmutativa : 3 × -2 = -2 x 3 = -6.
Aplicando la misma interpretación de la "multiplicación por un número negativo" para un valor que también es negativo, tenemos:
| -4 × -3 | = - (-4) - (-4) - (-4) |
| = 4 + 4 + 4 | |
| = 12 |
Sin embargo, desde un punto de vista formal, la multiplicación de dos números negativos es recibida directamente por medio de la distributividad de la multiplicación sobre la suma:
| -1 × -1 | |
| = (-1) X (-1) + (-2) + 2 | |
| = (-1) X (-1) + (-1) × 2 + 2 | |
| = (-1) X (-1 + 2) + 2 | |
| = (-1) X 1 + 2 | |
| = (-1) + 2 | |
| = 1 |
División
División es similar a la multiplicación. Brahmagupta declaró por primera vez que negativo dividido por negativo a positivo. Dividido positiva por negativa a ser negativo. (Referencia: Aritmética y medición de Brahmagupta por HT Colebrooke). Convención de Brahmagupta ha sobrevivido hasta la fecha: si el dividendo y divisor tienen diferentes signos, entonces el resultado es negativo.
- 8 / -2 = -4
- -10/2 = -5
Si dividendo y el divisor tienen el mismo signo, el resultado es positivo, aunque ambos son negativos.
- -12 / -3 = 4
Construcción formal de los números enteros negativos y no negativos
De una manera similar a los números racionales , podemos extender el números naturales a la N números enteros Z mediante la definición de números enteros como una par ordenado de números naturales (a, b). Podemos extender la suma y la multiplicación de estas parejas con las siguientes reglas:
- (A, b) + (c, d) = (a + c, b + d)
- (A, b) × (c, d) = (a × c + b × d, a × d + b × c)
Definimos una relación de equivalencia ~ sobre estos pares con la siguiente regla:
- (A, b) ~ (c, d) si y sólo si a + d = b + c.
Esta relación de equivalencia es compatible con la adición y multiplicación se define anteriormente, y podemos definir Z para ser el cociente establecido N ² / ~, es decir, identificamos dos pares (a, b) y (c, d) si son equivalentes en el sentido anterior.
También podemos definir una orden total en Z por escrito
- (A, b) ≤ (c, d) si y sólo si a + d ≤ b + c.
Esto conducirá a un aditivo cero de la forma (a, a), un inverso aditivo de (a, b) de la forma (b, a), una unidad multiplicativo de la forma (a + 1, a), y una definición de la resta
- (A, b) - (c, d) = (a + d, b + c).
Primer uso de números negativos
Durante mucho tiempo, las soluciones a los problemas negativos fueron considerados "falso" porque no se pudo encontrar en el mundo real (en el sentido de que no se puede, por ejemplo, tener un número negativo de semillas). El concepto abstracto fue reconocido ya en 100 aC - 50 aC A Obra china, Nueve capítulos del arte matemático (Jiu zhang suanshu), contiene métodos para encontrar las áreas de figuras; rojo varillas de conteo se utilizaron para denotar positivo coeficientes, barras negras para negativo. Los chinos también fueron capaces de resolver ecuaciones simultáneas con números negativos. La antigua india Bakhshali manuscrito, que fue escrito en algún momento entre el 200 aC y el 300 dC, realiza cálculos con números negativos, con un "+" como un signo negativo. Estos son los usos más antiguos conocidos de los números negativos.
En Egipto helenístico, Diofanto en el siglo III dC se refirió a una ecuación que era equivalente a 4 x + 20 = 0 (que tiene una solución negativa) en Aritmética, diciendo que la ecuación era absurdo. Esto indica que el concepto de números negativos existía en el Mediterráneo antiguo.
Durante el siglo VII de nuestra era, se utilizaron los números negativos en la India para representar deudas. El matemático indio Brahmagupta , en Brahma-Sphuta-Siddhanta (escrito en AD 628), discutió el uso de números negativos para producir la forma general fórmula cuadrática que sigue en uso hoy en día. También encontró soluciones negativas de las ecuaciones cuadráticas y dio normas relativas a las operaciones con números negativos y cero , como "Una deuda cortado de la nada se convierte en un crédito;. un crédito separado de la nada se convierte en una deuda" Llamó a los números positivos "fortunas, una cifra "cero", "y los números negativos" deudas ".
Durante el siglo VIII dC, la Mundo islámico se enteró de los números negativos de árabe traducciones de obras de Brahmagupta, y por AD 1000 matemáticos árabes estaban usando números negativos por las deudas.
En el duodécimo siglo DC en la India, Bhaskara también dio raíces negativas para ecuaciones de segundo grado, pero los rechazó porque eran inapropiadas en el contexto del problema. Afirmó que un valor negativo es "en este caso no se debe tomar, pues es inadecuada, la gente no aprueban raíces negativas."
El conocimiento de los números negativos, finalmente, llegó a Europa a través Latina traducciones de árabe y obras indias.
Europeos matemáticos, en su mayor parte, resistieron el concepto de números negativos hasta el siglo 17 , aunque Fibonacci permitió soluciones negativas en problemas financieros, donde podrían ser interpretadas como débitos (capítulo 13 del Ábacos de Liber, AD 1202) y más tarde como pérdidas (en Flos). En este momento, los chinos estaban indicando los números negativos dibujando un trazo diagonal a través de la más a la derecha que no sea cero dígitos.
En el siglo 15, Nicolas Chuquet, un francés, utiliza los números negativos como exponentes y se refirió a ellos como "los números absurdos."
En AD 1759, Francis Maseres, un matemático Inglés, escribió que los números negativos "oscurecen muy enteras las doctrinas de las ecuaciones y hacen oscuro de las cosas que están en su naturaleza excesivamente obvia y simple". Llegó a la conclusión de que no existían los números negativos.
Los números negativos no fueron bien comprendidas hasta los tiempos modernos. Tan recientemente como en el siglo 18 , el suizo matemático Leonhard Euler cree que los números negativos fueron mayores que el infinito , un punto de vista que fue compartido por John Wallis. Era una práctica común en ese tiempo de ignorar ningún resultado negativos derivados de ecuaciones, en el supuesto de que no tenían sentido. ( refactorizada de 4) El argumento de que los números negativos son mayores que el infinito implicado el cociente 1 / x, y teniendo en cuenta lo que ocurre cuando x tiende y cruza el punto x = 0 desde el lado positivo.