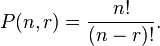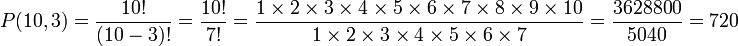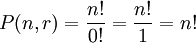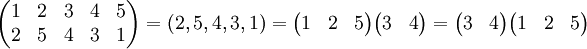Permutación

En varios campos de las matemáticas el término permutación se utiliza con diferentes pero estrechamente relacionados significados. Todos ellos se refieren a la noción de (re) organización de elementos de una determinada finito establecer en una secuencia .

Definiciones

El concepto general de permutación se puede definir de manera más formal en diferentes contextos:

En la combinatoria

En combinatoria , una permutación se entiende generalmente para ser una secuencia que contiene cada elemento de un conjunto finito de una vez, y sólo una vez. El concepto de secuencia es distinta de la de un conjunto, en el que los elementos de una secuencia aparecen en algún orden: la secuencia tiene un primer elemento (menos que esté vacía), un segundo elemento (a menos que su longitud es inferior a 2), etcétera. En contraste, los elementos de un conjunto no tienen un orden; {1, 2, 3} y {3, 2, 1} son diferentes maneras de denotar el mismo conjunto.

Sin embargo, también hay un significado más general tradicional del término "permutación" usado en la combinatoria. En este sentido más general, permutaciones son aquellas secuencias en las que, como antes, cada elemento se produce en más de una vez, pero no todos los elementos del conjunto dado deben ser utilizados.

Para una noción relacionada en la que el orden de los elementos seleccionados formar un conjunto, para que el orden es irrelevante, ver Combinación.

En la teoría de grupos

En la teoría de grupos y áreas relacionadas, los elementos de una permutación no necesitan estar dispuestos en una orden lineal, o de hecho en cualquier orden en absoluto. Bajo esta definición refinada, una permutación es un biyección de una finito establecido sobre sí mismo. Esto permite la definición de los grupos de permutaciones; ver Grupo de la permutación.

Contando permutaciones

En sólo esta sección, la definición tradicional de la combinatoria se utiliza: una permutación es una secuencia ordenada de elementos seleccionados de un conjunto finito dado, sin repeticiones, y no necesariamente el uso de todos los elementos del conjunto dado. Por ejemplo, dado el conjunto de letras {C, E, G, I, N, R}, algunas permutaciones son RING, ARROZ, MÁS AGRADABLE, REINADO y se estremecen, pero también RNCGI -. La secuencia no tiene que deletrear una palabra existente MOTOR , por otro lado, no es una permutación, ya que utiliza los elementos E y N dos veces.

Si n denota el tamaño del conjunto - el número de elementos disponibles para la selección - y permutaciones sólo se consideran que utilizan todos los elementos N, entonces el número total de permutaciones posibles es igual a n, donde! "!" es el factorial operador. Esto se puede mostrar de manera informal como sigue. En la construcción de una permutación, hay n posibles opciones para el primer elemento de la secuencia. Una vez que ha sido elegido,

elementos se dejan, por lo que para el segundo elemento sólo hay

posibles opciones. Durante los primeros dos elementos juntos, eso nos da

n × (n - 1) permutaciones posibles.

Para seleccionar el tercer elemento, hay entonces

elementos de la izquierda, dando, durante los tres primeros elementos,

n × (n - 1) × (n - 2) permutaciones posibles.

Continuando de esta manera hasta que sólo hay 2 elementos de la izquierda, hay 2 opciones, dando para el número de permutaciones posibles que constan de

elementos:

n × (n - 1) × (n - 2) × ... × 2.

La última opción se ve obligado, ya que no es exactamente un elemento izquierdo. En una fórmula, esto es el número

n × (n - 1) × (n - 2) × ... × 2 × 1

(Que es el mismo que antes, porque el factor 1 no hace una diferencia). Este número es, por definición, el mismo que n!.

En general, el número de permutaciones se denota por P (n, r), _n P _r o a veces 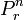, Donde:

• n es el número de elementos disponibles para la selección, y
• r es el número de elementos a seleccionar (0 ≤ r ≤ n).

Para el caso en

sólo se ha demostrado que

. El caso general es dada por la fórmula:

Como antes, esto se puede demostrar de manera informal considerando la construcción de una permutación arbitraria, pero este tiempo de parada cuando se ha alcanzado la longitud r. La construcción procede inicialmente como arriba, pero se detiene en longitud r. El número de posibles permutaciones que se ha alcanzado entonces es:

P (n, r) = n × (n - 1) x (n - 2) x ... x (n - r + 1).

Por lo tanto:

n! N = x (n - 1) x (n - 2) ... × × 2 × 1

N = x (n - 1) x (n - 2) x ... x (n - r + 1) x (n - r) × ... × 2 × 1

= P (n, r) x (n - r) × ... × 2 × 1

= P (n, r) x (n - r) !.

Pero si n! = P (n, r) x (n - r) !, entonces

. Por ejemplo, si hay un total de 10 elementos y están seleccionando una secuencia de tres elementos de este conjunto, entonces la primera selección es uno de 10 elementos, la siguiente de la restante 9 y, finalmente, a partir de los 8 restantes, dando

. En este caso, n = 10 y R = 3. Usando la fórmula para calcular P (10,3),

En el caso especial donde n = r la fórmula anterior se simplifica a:

La razón por 0! = 1 es que 0! es una vacío producto, que siempre es igual a 1.

En el ejemplo dado en el encabezado de este artículo, con 6 números enteros {1..6}, esto sería: P (6,6) = 6! / (6-6)! = (1 × 2 × 3 × 4 × 5 × 6) / 0! = 720/1 = 720.

Otras notaciones, mayores incluyen ⁿ P _r, P _{n, r,} o _n P _r. Una notación moderna común es (n) _r que se llama una cayendo factorial. Sin embargo, la misma notación se utiliza para el aumento factorial (también llamado Símbolo Pochhammer)

n (n + 1) (n + 2) ⋯ (n + r - 1) r.

Con la notación factorial en aumento, el número de permutaciones es (n - r + 1) _r.

Permutaciones en la teoría de grupos

Como se explica en la sección anterior, en la teoría de grupos el término permutación (de un conjunto) se reserva a una mapa biyectiva ( biyección) a partir de un conjunto finito sobre sí mismo. El ejemplo anterior, de hacer permutaciones de números de 1 a 10, se traduce como un mapa del conjunto {1, ..., 10} para sí mismo.

Notación

Hay dos notaciones principales para tales permutaciones. En la notación de relación, uno puede organizar el orden "natural" de los elementos que se permutó en una fila, y el nuevo ordenamiento en otra fila:

representa el s permutación del conjunto {1,2,3,4,5} definido por s (1) = 2, S (2) = 5, S (3) = 4, s (4) = 3, s (5) = 1.

Si tenemos un conjunto finito E de n elementos, es por definición en biyección con el conjunto {1, ..., n}, donde esta biyección f corresponde sólo a la numeración de los elementos. Una vez que se numeran, podemos identificar las permutaciones del conjunto E con permutaciones del conjunto {1, ..., n}. (En términos más matemáticos, la función que mapea un s permutación de E para la permutación fosof ^-1 de {1, ..., n} es una morfismo de la grupo simétrico de E en el de {1, ..., n}, ver más abajo.)

Alternativamente, se puede escribir la permutación en términos de cómo los elementos cambian cuando se aplica sucesivamente la permutación. Esto se conoce como la descomposición de la permutación en un producto de disjuntos ciclos. Funciona de la siguiente manera: a partir de un elemento x, escribimos la secuencia (x s (x) s ² (x), ...) hasta que regresemos el elemento inicial (momento en el que cerramos el paréntesis sin escribirla por segunda vez ). Esto se llama el ciclo asociado a x 's orbitar siguiente s. Luego tomamos un elemento que no escribimos con todo y hacemos lo mismo, hasta que hemos considerado todos los elementos. En el ejemplo anterior, obtenemos: s = (1 2 5) (3 de 4).

Cada ciclo (x ₁ x ₂ ... x _L) representa la permutación que los mapas x _i x _i en ₁ (i = 1 ... L -1) y x _L x en _1, y deja todos los demás elementos invariante. L se llama la longitud del ciclo. Puesto que estos ciclos tienen por la construcción desarticular soportes (es decir, actúan no trivial en subconjuntos disjuntos de E), que hacen viaje (por ejemplo, (1 2 5) (3 4) = (3 4) (1 2 5)). El orden de los ciclos en el (composición) de productos no importa, mientras que el orden de los elementos en cada uno de los ciclos que importa ( hasta el cambio cíclico; ver también ciclos y puntos fijos).

Obviamente, a 1 ciclo (ciclo de longitud 1) es la misma que la fijación del elemento que figura en él, por lo que no sirve de nada por escrito de forma explícita. Definición de un ciclo Algunos autores no incluyen ciclos de longitud 1.

Ciclos de longitud dos se llaman transposiciones; tales permutaciones simplemente intercambiar el lugar de dos elementos. (A la inversa, una transposición de la matriz es en sí mismo un ejemplo importante de una permutación.)

Producto e inversa de permutaciones

Uno puede definir el producto de dos permutaciones como sigue. Si tenemos dos permutaciones, P y Q, la acción de la primera realización de P y luego Q será la misma que la realización de algún sola permutación R. El producto de P y Q se define entonces ser que permutación R. Visualización de permutaciones como biyecciones, el producto de dos permutaciones es por lo tanto el mismo como su composición como funciones. No hay notación universalmente acordado para la operación del producto entre permutaciones, y dependiendo de la autora una fórmula como PQ puede significar P ∘ Q o Q ∘ P. Desde la composición de funciones es asociativa , por lo que es el funcionamiento del producto en permutaciones: (P ∘ Q) ∘ R = P ∘ (Q ∘ R).

Asimismo, puesto biyecciones tienen inversas , también lo hacen las permutaciones, y ambos ∘ P P P ^-1 y ^-1 ∘ P son el "permutación identidad" (ver más abajo) que deja todas las posiciones sin cambios. Así, puede verse que las permutaciones forman un grupo .

Como para cualquier grupo, hay una isomorfismo de grupo en los grupos de permutaciones, obtenidos mediante la asignación a cada permutación su inversa, y esto es un isomorfismo involución, dando una visión dual sobre cualquier resultado abstracto. Puesto que (P ∘ Q) ^-1 = Q ^-1 ∘ ^P-1, desde un punto de vista abstracto, será indiferente que PQ representa "P Q antes" o "después de P Q". Para permutaciones de hormigón, la distinción es, por supuesto, bastante material.

Permutaciones especiales

Si pensamos en una permutación que "cambia" la posición del primer elemento al primer elemento, el segundo a la segunda, y así sucesivamente, que realmente no han cambiado las posiciones de los elementos en absoluto. Debido a su acción, lo describimos como la permutación identidad, ya que actúa como un función identidad. A la inversa, una permutación que cambia la posición de todos los elementos (sin elemento se asigna a sí mismo) se llama una desarreglo.

Si uno tiene alguna permutación, llamada P, se puede describir una permutación, P ^-1 escrito, que deshace la acción de aplicación de P. En esencia, la realización de P entonces P ^-1 es equivalente a realizar la permutación identidad. Uno siempre tiene una permutación tal desde una permutación es un mapa biyectiva. Tal una permutación se llama permutación inversa. Se calcula mediante el intercambio de cada número y el número del lugar que ocupa.

Una incluso permutación es una permutación que se puede expresar como el producto de un número par de transposiciones, y la permutación identidad es una permutación par ya que es igual a (1 2) (1 2). Una permutación impar es una permutación que se puede expresar como el producto de un número impar de transposiciones. Se puede demostrar que cada permutación es par o impar y no puede ser a la vez.

Una teorema acerca de la permutación inversa es el efecto de una conjugación de una permutación por una permutación en un grupo de permutación. Si tenemos una permutación Q = (i ₁ i ₂ ... i _n) y una permutación P, entonces PQP ^-1 = (P (i ₁₎ P (i ₂₎ ... P (i _n)).

También podemos representar una permutación en matriz de la forma; la matriz resultante se conoce como una matriz de permutación.

Las permutaciones en informática

Algunos de los libros de texto de más edad vistazo a permutaciones como asignaciones, como se mencionó anteriormente. En ciencias de la computación términos, se trata de operaciones de asignación, con valores

1, 2, ..., n

asignados a las variables

x _1, x _2, ..., x _n.

Cada valor se debe asignar una sola vez.

La diferencia de asignación / sustitución es entonces ilustrativa de una manera en la que programación funcional y programación imperativa diferir - programación funcional pura no tiene ningún mecanismo de asignación. La convención matemática es hoy en día que las permutaciones son sólo las funciones y el funcionamiento de ellos es la composición de funciones ; programadores funcionales siguen este. En el lenguaje asignación de una sustitución es una instrucción para cambiar ronda los valores asignados, de forma simultánea; un problema bien conocido.

Numeración permutaciones

Números Factoradic pueden utilizarse para asignar números únicos a permutaciones, de tal manera que da un factoradic de k uno puede encontrar rápidamente la permutación correspondiente.

Algoritmos para generar permutaciones

Generación desordenada

! Por cada número k, con 0 ≤ k <n, el siguiente algoritmo genera una permutación única de la secuencia inicial s _j, j = 1 ... n:

  permutación función (k, s) {
      var int factorial: = 1;
      para j = 2 a la longitud (s) {
         factorial: = factorial * (j-1);  // Factorial = (j-1)!
         canje s [j- ((k / factorial) j mod)] con s [j];
      }
      volver s;
  }

Generación orden lexicográfico

! Por cada número k, con 0 ≤ k <n, el siguiente algoritmo genera la correspondiente permutación lexicográfica de la secuencia inicial s _j, j = 1 ... n:

  permutación función (k, s) {
      var int n: = longitud (s);  factorial: = 1;
      para j = 2 a n-1 {// calcular (n- 1)!
          factorial: = factorial * j;
      }
      para j = 1 a n-1 {
          tempj: = (/ factorial k) mod (n + 1- j);
          temps: = s [j + tempj]
          para i = j + tempj a j + 1 paso -1 {
              s [i]: = s [i-1];  // Cambiar el derecho cadena
          }
          s [j]: = temps;
          factorial: = factorial / (j n-);
      }
      volver s;
  }

Notación

• k / j denota la división entera de k por j, es decir, la integral cociente sin ningún resto, y
• mod k j es el resto siguiente división entera de k por j.
• s [n] denota el enésimo elemento de la secuencia s.

Implementaciones de software y hardware

Funciones de cálculo

La mayoría de las calculadoras tienen una función incorporada para calcular el número de permutaciones, llamado nPr o PERM en muchos. La función de permutaciones es a menudo sólo está disponible a través de varias capas de menús; cómo acceder a la función viene a menudo indicada en la documentación de las calculadoras que lo apoyan.

Funciones de hoja de cálculo

Más software de hoja de cálculo también proporciona una función incorporada para calcular el número de permutaciones, llama PERMUTACIONES en muchas hojas de cálculo populares. Apple Números software en particular no incluye actualmente una función de este tipo.