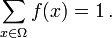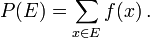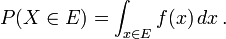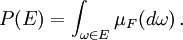Teoría de la probabilidad
Sabías ...
SOS cree que la educación da una mejor oportunidad en la vida para los niños en el mundo en desarrollo también. Con Infantil SOS se puede elegir a apadrinar a los niños en más de cien países
Teoría de la probabilidad es la rama de las matemáticas interesados en el análisis de fenómenos aleatorios. Los objetos centrales de la teoría de la probabilidad son variables aleatorias , procesos estocásticos, y eventos: abstracciones matemáticas de eventos no deterministas o cantidades medidas que pueden ser ya sea ocurrencias individuales o evolucionar con el tiempo de una manera aparentemente aleatoria. Aunque una moneda individuo lanzamiento o el rollo de una matriz es un evento al azar, si se repite muchas veces la secuencia de eventos aleatorios exhibirá ciertos patrones estadísticos, que se pueden estudiar y predecir. Dos resultados matemáticos representativos que describen tales patrones son la ley de los grandes números y el teorema del límite central.
Como fundamento matemático para las estadísticas , teoría de la probabilidad es esencial para muchas actividades humanas que implican el análisis cuantitativo de grandes conjuntos de datos. Los métodos de la teoría de probabilidades se aplican también a la descripción de los sistemas complejos se obtienen sólo un conocimiento parcial de su estado, como en la mecánica estadística . Un gran descubrimiento del siglo XX la física fue la naturaleza probabilística de los fenómenos físicos a escalas atómicas, descritos en la mecánica cuántica .
Historia
La teoría matemática de la probabilidad tiene sus raíces en los intentos de analizar juegos de azar por Gerolamo Cardano en el siglo XVI, y por Pierre de Fermat y Blaise Pascal en el siglo XVII (por ejemplo el " problema de los puntos ").
Inicialmente, teoría de la probabilidad considerada principalmente eventos discretos, y sus métodos eran principalmente combinatoria . Finalmente, analíticos consideraciones obligaron a la incorporación de las variables continuas en la teoría. Esto culminó en teoría de la probabilidad moderna, los cimientos de lo que fueron puestos por Andrey Nikolaevich Kolmogorov. Kolmogorov combina la noción de espacio muestral, introducido por Richard von Mises, y teoría de la medida y presentó su sistema de axiomas de la teoría de probabilidades en 1933. Bastante rápidamente se convirtió en el indiscutible base axiomática de la teoría de probabilidades moderna.
Tratamiento
La mayoría de las introducciones a la teoría de probabilidades tratan las distribuciones de probabilidad discretas y las distribuciones de probabilidad continuas por separado. El tratamiento basado en la teoría de medida más matemáticamente avanzado de probabilidad abarca tanto el discreto, el continuo, cualquier combinación de estos dos y más.
Distribuciones de probabilidad discretas
Teoría de la probabilidad discreta se ocupa de los eventos que ocurren en espacios muestrales contables.
Ejemplos: Lanzar los dados , los experimentos con barajas de cartas , y paseo aleatorio.
Definición clásica: Inicialmente la probabilidad de que suceda un evento se define como el número de casos favorables para el evento, sobre el número de resultados totales posibles en un espacio muestral equiprobable.
Por ejemplo, si el evento es "ocurrencia de un número par cuando un troquel se enrolla ", la probabilidad viene dada por 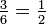 , Desde hace 3 caras de los 6 tienen números pares y cada cara tiene la misma probabilidad de aparecer.
, Desde hace 3 caras de los 6 tienen números pares y cada cara tiene la misma probabilidad de aparecer.
Definición moderna: La definición moderna comienza con un conjunto llamado espacio de muestra, que se refiere al conjunto de todos los resultados posibles en sentido clásico, denotado por 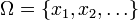 . Se supone entonces que para cada elemento
. Se supone entonces que para cada elemento 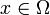 , Una "probabilidad" valor intrínseco
, Una "probabilidad" valor intrínseco 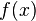 se adjunta, que satisface las siguientes propiedades:
se adjunta, que satisface las siguientes propiedades:
Es decir, la función de probabilidad f (x) se encuentra entre cero y uno para cada valor de x en el espacio muestral Ω, y la suma de f (x) sobre todos los valores de x en el espacio muestral Ω es exactamente igual a 1. Un evento se define como cualquier subconjunto 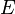 del espacio muestral
del espacio muestral 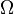 . La probabilidad del evento
. La probabilidad del evento 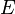 definido como
definido como
Por lo tanto, la probabilidad de que todo el espacio de la muestra es 1, y la probabilidad del evento nula es 0.
La función 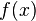 la asignación de un punto en el espacio de muestra con el valor "probabilidad" se llama función de probabilidad abreviado como pmf. La definición moderna no intenta responder cómo se obtienen las funciones de masa de probabilidad; en lugar de ello construye una teoría que asume su existencia.
la asignación de un punto en el espacio de muestra con el valor "probabilidad" se llama función de probabilidad abreviado como pmf. La definición moderna no intenta responder cómo se obtienen las funciones de masa de probabilidad; en lugar de ello construye una teoría que asume su existencia.
Distribuciones de probabilidad continuas
Teoría de la probabilidad continua se ocupa de los eventos que ocurren en un espacio muestral continuo.
Definición clásica: La definición clásica se rompe cuando se enfrenta con el caso continuo. Ver La paradoja de Bertrand.
Definición moderna: Si el espacio muestral es los números reales ( 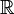 ), A continuación, una función de llamada función de distribución acumulativa (o CDF)
), A continuación, una función de llamada función de distribución acumulativa (o CDF) 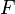 se supone que existe, lo que da
se supone que existe, lo que da 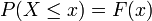 para una variable aleatoria X. Es decir, F (x) devuelve la probabilidad de que X será menor que o igual a x.
para una variable aleatoria X. Es decir, F (x) devuelve la probabilidad de que X será menor que o igual a x.
La CDF debe satisfacer las siguientes propiedades.
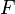 es un monotónicamente no decreciente, función continua por la derecha;
es un monotónicamente no decreciente, función continua por la derecha; 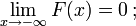
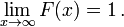
Si 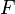 es diferenciable, entonces se dice que la variable aleatoria X para tener una función de densidad de probabilidad o pdf o simplemente densidad
es diferenciable, entonces se dice que la variable aleatoria X para tener una función de densidad de probabilidad o pdf o simplemente densidad 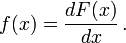
Para un conjunto 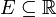 , La probabilidad de que la variable aleatoria X estar en
, La probabilidad de que la variable aleatoria X estar en 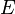 se define como
se define como
En caso de que exista la función de densidad de probabilidad, esto puede escribirse como
Mientras exista el pdf sólo para variables aleatorias continuas, existe la cdf para todas las variables aleatorias (incluyendo variables aleatorias discretas) que toman valores en 
Estos conceptos se pueden generalizar para casos multidimensionales sobre 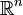 y otros espacios muestrales continuos.
y otros espacios muestrales continuos.
Teoría de la probabilidad Mida teórico-
La razón de ser de la medida con el tratamiento teórico de la probabilidad es que unifica lo discreto y lo continuo, y hace que la diferencia de una cuestión de la que se utiliza la medida. Además, cubre las distribuciones que no son ni discretas ni continuas ni mezclas de los dos.
Un ejemplo de tales distribuciones podría ser una mezcla de distribuciones discretas y continuas, por ejemplo, una variable aleatoria que es 0 con una probabilidad de 1/2, y toma un valor de la distribución aleatoria normal con probabilidad media. Todavía se puede estudiar en cierta medida por considerarla tener un pdf de ![(\ Delta [x] + \ varphi (x)) / 2](../../images/493/49348.png) , Donde
, Donde ![\ Delta [x]](../../images/493/49349.png) es el Función delta de Kronecker.
es el Función delta de Kronecker.
Otras distribuciones pueden incluso no ser una mezcla, por ejemplo, el Distribución de Cantor no tiene probabilidad positiva para cualquier punto único, ni tampoco tiene una densidad. El enfoque moderno de la teoría de la probabilidad resuelve estos problemas mediante teoría de la medida para definir el espacio de probabilidad :
Dado cualquier conjunto 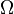 , (También llamado espacio de muestra) y una σ-álgebra
, (También llamado espacio de muestra) y una σ-álgebra 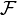 en ella, una medir
en ella, una medir 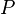 se llama una medida de probabilidad si
se llama una medida de probabilidad si
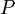 es no negativo;
es no negativo; 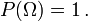
Si 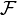 es un Borel σ-álgebra entonces hay una medida de probabilidad única en
es un Borel σ-álgebra entonces hay una medida de probabilidad única en 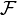 para cualquier función de distribución, y viceversa. La medida corresponde a una función de distribución se dice que es inducida por la CDF. Esta medida coincide con la pmf para variables discretas y pdf para las variables continuas, por lo que el enfoque de la teoría de medida libre de falacias.
para cualquier función de distribución, y viceversa. La medida corresponde a una función de distribución se dice que es inducida por la CDF. Esta medida coincide con la pmf para variables discretas y pdf para las variables continuas, por lo que el enfoque de la teoría de medida libre de falacias.
La probabilidad de un conjunto 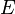 en la σ-álgebra
en la σ-álgebra 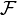 se define como
se define como
donde la integración es con respecto a la medida 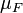 inducida por
inducida por 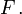
Además de proporcionar una mejor comprensión y unificación de probabilidades discretas y continuas, el tratamiento teórico-medida también nos permite trabajar en probabilidades fuera 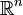 , Como en la teoría de la procesos estocásticos. Por ejemplo, para estudiar El movimiento browniano, la probabilidad se define en un espacio de funciones.
, Como en la teoría de la procesos estocásticos. Por ejemplo, para estudiar El movimiento browniano, la probabilidad se define en un espacio de funciones.
Distribuciones de probabilidad
Ciertas variables aleatorias ocurren muy a menudo en la teoría de la probabilidad, ya que así se describen muchos procesos naturales o físicas. Sus distribuciones por lo tanto han adquirido especial importancia en la teoría de la probabilidad. Algunas distribuciones discretas fundamentales son la uniforme discreta, Bernoulli, binomial , binomial negativa, de Poisson y distribuciones geométricas. Distribuciones continuas importantes incluyen la uniforme continua, lo normal , exponencial , gamma y distribuciones beta.
La convergencia de las variables aleatorias
En teoría de la probabilidad, hay varias nociones de convergencia para variables aleatorias . Se enumeran a continuación en el orden de potencia, es decir, cualquier noción posterior de la convergencia en la lista implica la convergencia de acuerdo con todas las nociones anteriores.
- La convergencia en la distribución: Como su nombre lo indica, una secuencia de variables aleatorias
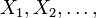 converge a la variable aleatoria
converge a la variable aleatoria 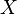 en la distribución si sus respectivas funciones de distribución acumulativa
en la distribución si sus respectivas funciones de distribución acumulativa 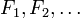 converger a la función de distribución acumulativa
converger a la función de distribución acumulativa 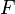 de
de 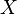 , Donde
, Donde 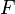 es continua.
es continua.
- Más común notación abreviada:
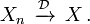
- Más común notación abreviada:
- Convergencia débil: La secuencia de variables aleatorias
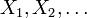 se dice que convergen hacia la variable aleatoria
se dice que convergen hacia la variable aleatoria 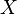 débilmente si
débilmente si 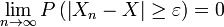 para cada ε> 0. convergencia débil también se llama convergencia en probabilidad.
para cada ε> 0. convergencia débil también se llama convergencia en probabilidad.
- Más común notación abreviada:
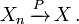
- Más común notación abreviada:
- Convergencia fuerte: La secuencia de variables aleatorias
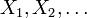 se dice que convergen hacia la variable aleatoria
se dice que convergen hacia la variable aleatoria 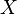 fuertemente si
fuertemente si 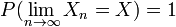 . Convergencia fuerte también se conoce como casi seguro de convergencia.
. Convergencia fuerte también se conoce como casi seguro de convergencia.
- Más común notación abreviada:
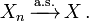
- Más común notación abreviada:
Intuitivamente, fuerte convergencia es una versión más fuerte de la convergencia débil, y en ambos casos las variables aleatorias 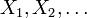 mostrar una correlación con el aumento de
mostrar una correlación con el aumento de 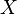 . Sin embargo, en caso de convergencia en la distribución, los valores realizados de las variables aleatorias no tienen que converger, y su posible correlación entre ellos es irrelevante.
. Sin embargo, en caso de convergencia en la distribución, los valores realizados de las variables aleatorias no tienen que converger, y su posible correlación entre ellos es irrelevante.
Ley de los grandes números
Intuición común sugiere que si una moneda es lanzada muchas veces, entonces más o menos la mitad del tiempo que a su vez a la cabeza, y la otra mitad va a subir colas. Además, cuanto más a menudo la moneda se lanza, lo más probable debe ser que la relación entre el número de cabezas con el número de colas se acercará a la unidad. Probabilidad Moderno ofrece una versión formal de esta idea intuitiva, conocida como la ley de los grandes números. Esta ley es notable porque se asume ninguna parte de los fundamentos de la teoría de la probabilidad, pero en su lugar emerge de estas fundaciones como un teorema. Desde que se vincula probabilidades derivadas teóricamente a su frecuencia real de ocurrencia en el mundo real, la ley de los grandes números se considera como un pilar en la historia de la teoría estadística.
La ley de los grandes números (LLN) señala que el promedio de la muestra 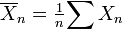 de
de 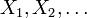 (Independiente e idénticamente distribuido variables aleatorias con expectativa finito
(Independiente e idénticamente distribuido variables aleatorias con expectativa finito 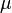 ) Converge hacia la expectativa teórica
) Converge hacia la expectativa teórica 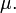
Es en las diferentes formas de convergencia de variables aleatorias que separa el débil y el fuerte ley de los grandes números
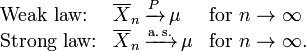
Se deduce de LLN que si se observa un evento de probabilidad p repetidamente durante experimentos independientes, la relación de la frecuencia observada de ese evento con el número total de repeticiones converge hacia p.
Poniendo esto en términos de variables aleatorias y LLN que tenemos 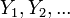 son independientes Variables aleatorias de Bernoulli que toman los valores 1 con probabilidad p y 0 con probabilidad 1- p.
son independientes Variables aleatorias de Bernoulli que toman los valores 1 con probabilidad p y 0 con probabilidad 1- p. 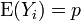 para todo i, y se sigue de LLN que
para todo i, y se sigue de LLN que 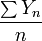 converge a p casi con toda seguridad.
converge a p casi con toda seguridad.
Teorema del límite central
El teorema del límite central explica la presencia en todas partes de la distribución normal en la naturaleza; es uno de los teoremas más famosos de probabilidad y estadística.
El teorema establece que la promedio de muchas variables aleatorias independientes e idénticamente distribuidas con varianza finita tiende hacia una distribución normal , independientemente de la distribución seguida por las variables aleatorias originales. Formalmente, y mucho 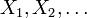 variables aleatorias independientes con media
variables aleatorias independientes con media 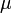 y varianza
y varianza 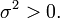 A continuación, la secuencia de variables aleatorias
A continuación, la secuencia de variables aleatorias
converge en distribución a una normal estándar variable aleatoria.

![f (x) \ in [0,1] \ mbox {para todos} x \ in \ Omega \ ,;](../../images/493/49335.png)