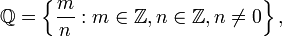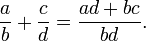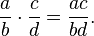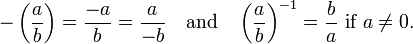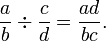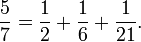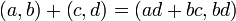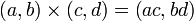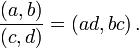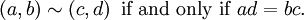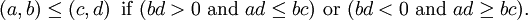Número racional

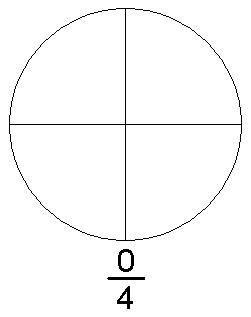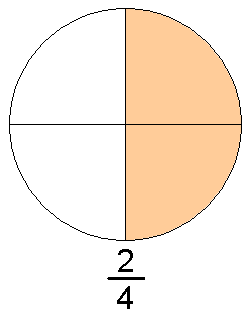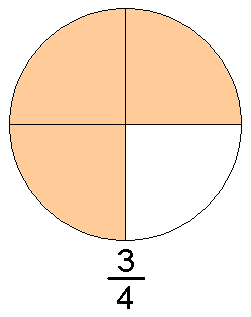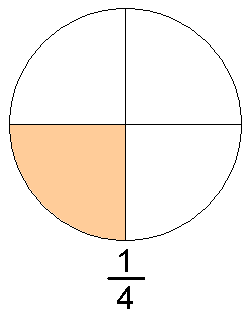
En las matemáticas , un número racional es un número que puede expresarse como una relación de dos números enteros . Números racionales no enteros (comúnmente llamados fracciones ) se escriben normalmente como la fracción vulgar 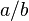, Donde b es no cero . a se llama el numerador , y B el denominador .

Cada número racional se puede escribir en un número infinito de formas, tales como 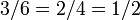, Pero se dice que es en la forma más simple cuando A y B no tienen comunes divisores excepto 1 (es decir, son primos entre sí). Cada número racional no nulo tiene exactamente una forma más simple de este tipo con un denominador positivo. Una fracción de esta forma más simple se dice que es una fracción irreducible, o una fracción en forma reducida.

La la expansión decimal de un número racional es eventualmente periódica (en el caso de una expansión finita los ceros que siguen implícitamente que forman la parte periódica). Lo mismo es cierto para cualquier otra base integral encima de uno, y también es cierto cuando los números racionales se consideran números p-adic en lugar de los números reales . A la inversa, si la expansión de un número para una base es periódica, es periódica para todas las bases y el número es racional. Un número real que no es un número racional se llama un número irracional .

Cuarteles

La conjunto de los números racionales, que constituye una campo, se denota 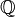. Usando el notación set-constructor, 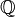se define como

donde 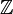denota el conjunto de los números enteros.

El término racional

En el mundo matemático, el adjetivo racional a menudo significa que el subyacente campo considerado es el campo 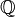números de racionales. Por ejemplo, un número entero racional es una algebraica número entero que es también un número racional, es decir, un número entero ordinario, y una racional matriz es una matriz cuyos coeficientes son números racionales. Polinomio racional generalmente, y lo más correctamente, significa un polinomio con coeficientes racionales, también llamado un "polinomio sobre los números racionales". Sin embargo, función racional no significa que el campo subyacente es los números racionales, y un curva algebraica racional no es una curva algebraica con coeficientes racionales.

Aritmética

Dos números racionales 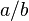y 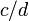son iguales si y solo si .

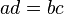Dos fracciones se añaden como sigue

La regla de la multiplicación es

Aditivo y existen inversos multiplicativos en los números racionales

De ello se deduce que el cociente de dos fracciones está dada por

Fracciones egipcias

Cualquier número racional positivo se puede expresar como una suma de distinta recíprocos de los números enteros positivos, tales como

Para cualquier número racional positivo, hay un número infinito de diferentes tales representaciones, llamadas Fracciones egipcias, ya que fueron utilizados por los antiguos Egipcios. Los egipcios también tenían una notación diferente para fracciones diádicas.

Construcción formal

Matemáticamente podemos construir los números racionales como clases de equivalencia de pares ordenados de números enteros 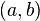, Con 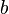no es igual a cero. Podemos definir la suma y la multiplicación de estas parejas con las siguientes reglas:

y si c ≠ 0, la división por

La intuición es que 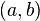representa el número indicado por la fracción 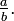Para cumplir con nuestra expectativa de que 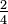y 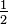denotar el mismo número, definimos una relación de equivalencia 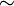en estos pares con la siguiente regla:

Esta relación de equivalencia es una Congruencia: es compatible con la adición y multiplicación se define anteriormente, y podemos definir Q ser el conjunto cociente de ~, es decir, identificamos dos pares (a, b) y (c, d) si son equivalentes en el sentido anterior. (Esta construcción puede llevarse a cabo en cualquier dominio integral: ver campo de fracciones.)

También podemos definir una orden total en Q por escrito

Los enteros pueden ser considerados como números racionales por parte de la incrustación de que los mapas 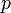a donde denota la clase de equivalencia que tiene 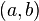como miembro.

Propiedades

un diagrama que ilustra la countabililty de los racionales

El conjunto 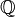, Junto con las operaciones de adición y multiplicación se muestran arriba, forma una campo, el campo de fracciones de los números enteros .

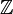Los números racionales son el campo más pequeño con característica cero: cada otro cuerpo de característica cero contiene una copia de 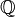. Los números racionales son por lo tanto el campo principal para característica cero.

La clausura algebraica de 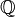, Es decir, el campo de las raíces de los polinomios racionales, es el números algebraicos.

El conjunto de todos los números racionales es contable. Dado que el conjunto de todos los números reales es incontable, decimos que casi todos los números reales son irracionales, en el sentido de Medida de Lebesgue, es decir, el conjunto de los números racionales es una conjunto nulo.

Los números racionales son un densamente conjunto ordenado: entre dos números racionales, allí está sentado otro, de hecho infinitamente muchos otros. Cualquier totalmente ordenado conjunto que es contable, denso (en el sentido más arriba), y no tiene ningún elemento menos o mayor es ordenar isomorfo a los números racionales.

Los números reales y las propiedades topológicas de los racionales

Los números racionales son un densa subconjunto de los números reales: todo número real tiene números racionales arbitrariamente cercanos a ella. Una propiedad relacionada es que los números racionales son los únicos números con expansiones finitos como fracciones continuas regulares.

En virtud de su orden, los racionales llevan un topología orden. Los números racionales también llevan una topología del subespacio. Los números racionales forman una espacio métrico mediante el uso de la métrica d (x, y) = | x - y |, y esto produce tercera topología en 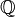. Las tres topologías coinciden y se convierten los números racionales en un campo topológico. Los números racionales son un ejemplo importante de un espacio que no es localmente compacto. Los números racionales se caracterizan topológicamente como la única contable espacio metrizable sin puntos aislados. El espacio es también totalmente desconectado. Los números racionales no forman una completar espacio métrico; los números reales son la finalización de .

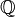p números -adic

Además de la métrica valor absoluto mencionado anteriormente, existen otras métricas que se convierten 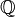en un campo topológico:

Dejar 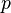ser un número primo y para cualquier número entero distinto de cero 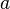dejar 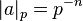, Donde 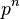es el más alto poder de 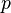divisorio ;

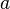Además de escritura 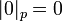. Para cualquier número racional 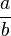, Establecimos .

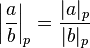Entonces 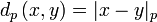define una métrica en .

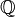El espacio métrico 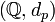no es completa, y su terminación es la p campo número -adic 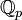. El teorema de Ostrowski establece que cualquier no trivial valor absoluto de los números racionales 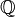es equivalente a ya sea el valor absoluto real, usual o una p-adic valor absoluto.