Teoría de conjuntos

La teoría de conjuntos es la rama de las matemáticas que estudia conjuntos, que son colecciones de objetos. Aunque cualquier tipo de objetos puede ser recogido en un conjunto, se aplica la teoría de conjuntos más a menudo a los objetos que son relevantes para las matemáticas.

El estudio moderno de la teoría de conjuntos fue iniciado por Cantor y Dedekind en la década de 1870. Tras el descubrimiento de las paradojas de la teoría de conjuntos informal, numerosos sistemas axiomáticos se propusieron a principios del siglo XX, de los cuales el Zermelo-Fraenkel axiomas, con la axioma de elección, son los más conocidos.

La teoría de conjuntos, formalizada mediante la lógica de primer orden , es el sistema fundamental más común para las matemáticas. El lenguaje de la teoría de conjuntos se utiliza en las definiciones de casi todos los objetos matemáticos, tales como funciones y conceptos de la teoría de conjuntos son integrados a través del currículo de matemáticas. Hechos elementales sobre conjuntos y establecer la pertenencia se pueden introducir en la escuela primaria, junto con los diagramas de Venn , para estudiar las colecciones de objetos físicos comunes. Operaciones elementales tales como la unión e intersección conjunto pueden ser estudiadas en este contexto. Conceptos más avanzados como cardinalidad son una parte estándar del currículo de matemáticas de pregrado.

Más allá de su uso como un sistema fundacional, la teoría de conjuntos es una rama de las matemáticas en su propio derecho, con una comunidad de investigación activa. La investigación contemporánea en la teoría de conjuntos incluye una variada colección de temas, que van desde la estructura del número real de línea para el estudio de la consistencia de grandes cardinales.

Historia

Ver Johnson (1972) para un tratamiento libro-longitud. Temas matemáticos típicamente emergen y se desarrollan a través de interacciones entre muchos investigadores. El punto de origen de la teoría de conjuntos es algo inusual, ya que puede ser identificado como un documento de 1874 por Georg Cantor : "En una propiedad característica de todos los números reales algebraicos".

A partir de la obra de Zeno alrededor de 450 aC, los matemáticos habían strugglinging con el concepto de infinito . Especialmente notable es el trabajo de Bernard Bolzano, en la primera mitad del siglo 19. La comprensión moderna de la infinidad comenzó 1867-1871, con Georg Cantor trabajo 's en la teoría de números. Una reunión de 1872 entre Cantor y Dedekind influenciado el pensamiento de Cantor y culminó en Cantor (1874).

El trabajo de Cantor inicialmente polarizada los matemáticos de su época. Mientras Weierstrass y Dedekind apoyó Cantor, Kronecker, ve ahora como uno de los fundadores de constructivismo matemático, no lo hizo. Sin embargo, la utilidad de conceptos tales como cantoriana uno-a-uno entre los juegos, su prueba de que hay más números reales que los enteros, y el "infinito de infinitos" ("el paraíso de Cantor") la funcionamiento conjunto potencia genera, finalmente llevó a la aceptación generalizada de la teoría de conjuntos cantoriana.

La próxima ola de entusiasmo en la teoría de conjuntos llegó alrededor de 1900, cuando se descubrió que cantoriana teoría de conjuntos dio lugar a varias contradicciones, llamadas antinomias o paradojas. Russell y Zermelo encontró independiente la paradoja más simple y el más conocido, que ahora se llama La paradoja de Russell y que implica "el conjunto de todos los conjuntos que no son miembros de sí mismos." Es evidente que este conjunto no puede ser miembro de sí misma, y por lo tanto debe ser un miembro de sí mismo! En 1899 Cantor mismo había planteado la pregunta: "¿cuál es el número cardinal ? del conjunto de todos los conjuntos " y obtuvo una paradoja relacionada. Más tarde se dio cuenta de que estas paradojas no se limitan a establecer la teoría, y que en la lógica de la frase "esta frase es falsa" da lugar a un problema similar, ya que si la sentencia es verdadera, debe ser falsa. Kurt Gödel utiliza este hecho en el 1931 una prueba de su célebre teorema de incompletitud.

El impulso de la teoría de conjuntos fue tal que el debate sobre las paradojas no condujo a su abandono. El trabajo de Zermelo en 1908 y Fraenkel en 1922 dio lugar a la canónica teoría axiomática de conjuntos ZFC, que está libre de paradojas. El trabajo de analistas como Lebesgue demostrado la gran utilidad matemática de la teoría de conjuntos. teoría axiomática de conjuntos se ha convertido tejida en la trama misma de la matemática como la conocemos hoy en día.

Conceptos básicos

La relación básica entre los objetos y conjuntos es el afiliación o relación "elementhood"; dado una O objeto y un conjunto A, ya sea O es un miembro de A o no es un miembro. La relación básica entre dos conjuntos es el subconjunto relación, también llamado conjunto de inclusión. Por ejemplo, {a, b} es un subconjunto de {a, b, c}, pero {a, d} no lo es.

Así como hay operaciones aritméticas que operan en números, hay operaciones en la teoría de conjuntos que operan sobre conjuntos. Por ejemplo, a partir de los conjuntos {1, 2, 3} y {2, 3, 4}, la operación de unión produce un nuevo conjunto {1, 2, 3, 4} que contiene todos los elementos que se encuentran en alguno de los conjuntos, y la intersección operación produce el conjunto {2, 3} que consta de todos los elementos que se encuentran en las dos series originales. Operaciones adicionales sobre conjuntos incluyen:

• Complementación: el conjunto de todos los elementos de un conjunto U que no están en un conjunto A se llama el complemento de A con respecto a U, denota 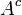. Esta terminología se utiliza con mayor frecuencia cuando U es un conjunto "universal" implict, como en el estudio de los diagramas de Venn . El conjunto de elementos de la U no en A también se llama la diferencia de conjuntos, que se denota .
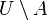• La diferencia simétrica de dos conjuntos consiste de todos los elementos que están en exactamente uno de los dos conjuntos.
• La Producto cartesiano de dos conjuntos A y B se compone de todos los pares ordenados (a, b) donde a es un miembro de A y B es un miembro de B.
• La powerset de un conjunto A se compone de todos los subconjuntos de A. Por ejemplo, el powerset de {1, 2} es {{}, {1}, {2}, {1,2}}.

Interpretaciones

Una idea clave en la teoría de conjuntos es el von Neumann universo de conjuntos puros. Un conjunto es puro si todos sus miembros son conjuntos, todos los miembros de sus miembros son conjuntos, y así sucesivamente. Por ejemplo, el conjunto que contiene sólo el conjunto vacío es un conjunto no vacío puro. Es común en la teoría de conjuntos para restringir la atención a los conjuntos de puros, en lugar de estudiar conjuntos arbitrarios, y muchos sistemas axiomáticos de la teoría de conjuntos sólo tienen la intención de axiomatizar los conjuntos puros.

Los conjuntos puros están dispuestos en la jerarquía acumulativa basada en la profundidad de sus miembros, los miembros de los miembros, etc. están anidados. Cada conjunto se le asigna un número ordinal α en esta jerarquía, conocido como su rango. Por el contrario, para cada ordinal α el conjunto V _α se define para contener todos los conjuntos que se asignan rango no mayor de α. La asignación de filas se hace recursión transfinito: si el extremo superior de las filas de los elementos de un conjunto X es α rango α entonces se asigna X + 1.

Teoría axiomática de conjuntos

Los conceptos básicos de la teoría de conjuntos se pueden estudiar de manera informal e intuitiva en lugar de axiomáticamente. De ahí que la teoría de conjuntos muy elemental puede ser enseñado en las escuelas primarias utilizando, por ejemplo, los diagramas de Venn . Este enfoque intuitivo da lugar a antinomias, el más simple y el más conocido de los cuales es Paradoja. De Russell teoría axiomática de conjuntos fue originalmente ideado para desterrar estas antinomias.

Los sistemas más ampliamente estudiado de la teoría de conjuntos se basan en el concepto de un jerarquía acumulativa de conjuntos. Estos sistemas son de dos tipos, aquellos cuya ontología consiste en:

• Establece solo. Esto incluye la teoría más común axiomática de conjuntos, Axiomas de Zermelo-Fraenkel (ZFC), que incluye el axioma de elección. Fragmentos de ZFC incluyen:
  • Axiomas de Zermelo-Fraenkel, que sustituye a la axioma esquema de reemplazo con la de separación;
  • La teoría de conjuntos General, un pequeño fragmento de Axiomas de Zermelo-Fraenkel suficiente para la Axiomas de Peano y conjuntos finitos;
  • Kripke-Platek la teoría de conjuntos, que omite los axiomas de la infinitud, powerset, y elección, y debilita los esquemas axioma de separación y reemplazo.
• Clases apropiadas, así como conjuntos. Esto incluye Von Neumann-Bernays-Gödel la teoría de conjuntos, que tiene la misma fuerza que ZFC de teoremas sobre conjuntos solos, y Morse-Kelley teoría de conjuntos, que es más fuerte que la ZFC.

Los sistemas NFU (con urelements) y NF (que carece de ellos) no se basan en una jerarquía acumulativa. NF y NFU incluyen un "conjunto de todos los conjuntos", en relación a que cada juego tiene un complemento. Por otro lado, NF (pero no NFU) permite que los sistemas de conjuntos para el cual el axioma de elección no se sostiene.

Sistemas de la teoría de conjuntos constructiva, como CST, CZF y IZF, incrustar sus axiomas establecidos en lógica intuicionista en lugar de la lógica de primer orden . Sin embargo, otros sistemas estándar aceptan la lógica de primer orden , pero cuentan con una relación de pertenencia no estándar. Éstos incluyen la teoría de conjuntos y áspera teoría de conjuntos difusos, en la que el valor de una fórmula atómica que incorpora la relación de pertenencia no es simplemente Verdadero y Falso. La Modelos de Boole con valores de ZFC son un tema relacionado.

Aplicaciones

Casi todos los conceptos matemáticos están formalmente definidos en términos de conjuntos y establecer conceptos teóricos. Por ejemplo, las estructuras matemáticas tan diversos como gráficos, colectores , anillos y espacios vectoriales son definidos como conjuntos que tienen diversas (axiomáticos) propiedades. Equivalencia y relaciones de orden son ubicuos en las matemáticas, con la teoría de las relaciones se basan enteramente en la teoría de conjuntos.

La teoría de conjuntos es también un sistema fundacional prometedor para gran parte de las matemáticas. Desde la publicación del primer volumen de Principia Mathematica, se ha afirmado que la mayoría o incluso todos los teoremas matemáticos se pueden derivar utilizando un conjunto de axiomas adecuadamente diseñado para la teoría de conjuntos, aumentada con muchas definiciones, utilizando en primera o segundo orden lógico. Por ejemplo, las propiedades de los naturales y los números reales pueden derivarse dentro de la teoría de conjuntos, ya que cada sistema de numeración puede ser identificado con un conjunto de clases de equivalencia en virtud de una adecuada relación de equivalencia cuyo campo es cierta conjunto infinito.

Teoría de conjuntos de base para el análisis matemático , topología , álgebra abstracta , y matemática discreta es igualmente indiscutible; matemáticos aceptan que (en principio) teoremas en estas áreas se pueden derivar de las definiciones y los axiomas de la teoría de conjuntos. Pocos derivaciones completos de teoremas matemáticos complejos a partir de la teoría de conjuntos se han verificado formalmente, sin embargo, debido a que tales derivaciones formales son a menudo mucho más largo que el lenguaje natural impermeabiliza matemáticos comúnmente presentes. Un proyecto de verificación, Metamath, incluye derivaciones de más de 10 mil teoremas a partir de la Axiomas ZFC y utilizando lógica de primer orden .

Las áreas de estudio

La teoría de conjuntos es un área importante de la investigación en matemáticas, con muchos sub-campos interrelacionados.

La teoría de conjuntos Combinatoria

La teoría de conjuntos Combinatoria refiere extensiones de finitos combinatoria de los conjuntos infinitos. Esto incluye el estudio de la aritmética cardinal y el estudio de las extensiones de Teorema de Ramsey como el Teorema de Erdos-Rado.

La teoría de conjuntos descriptiva

La teoría de conjuntos descriptiva es el estudio de diferentes grupos de la línea real y, más en general, los subconjuntos de Espacios polacos. Se inicia con el estudio de pointclasses en el Jerarquía Borel y se extiende hasta el estudio de las jerarquías más complejas tales como la jerarquía proyectiva y la Jerarquía Wadge. Muchas propiedades de los conjuntos de Borel se pueden establecer en ZFC, pero resultando estas propiedades se mantienen para los conjuntos más complicados requiere axiomas adicionales relacionados con la determinación y grandes cardenales.

El campo de la la teoría de conjuntos descriptiva efectivo se sitúa entre la teoría de conjuntos y teoría de la repetición. Incluye el estudio de pointclasses lightface, y está estrechamente relacionada con teoría hyperarithmetical. En muchos casos, los resultados de la teoría de conjuntos descriptiva clásica tienen versiones eficaces; en algunos casos, los nuevos resultados se obtienen mediante la prueba de la versión efectiva primero y luego se extiende ("relativizar") para hacerla más ampliamente aplicable.

Un área de investigación reciente de las preocupaciones Borel equivalencia relaciones y más complicados definibles relaciones de equivalencia . Esto tiene importantes aplicaciones en el estudio de invariantes en muchos campos de las matemáticas.

Teoría de conjuntos difusos

En la teoría de conjuntos como Cantor define y Zermelo y Fraenkel axiomatizada, un objeto es o un miembro de un conjunto o no. En teoría de conjuntos difusos esta condición se relajó por Zadeh por lo que un objeto tiene un grado de pertenencia a un conjunto, como número entre 0 y 1. Por ejemplo, el grado de pertenencia de una persona en el set de "gente alta" es más flexible que un simple sí o no hay respuesta y puede ser un número real como 0,75.

La teoría de modelos Interior

Un modelo interno de Axiomas de Zermelo-Fraenkel (ZF) es un transitivo clase que incluye a todos los ordinales y satisface todos los axiomas de ZF. El ejemplo canónico es la construible universo L desarrollado por Gödel. El estudio de los modelos de interiores de extensiones de ZF es de interés en la teoría de conjuntos, ya que puede ser usado para probar los resultados de consistencia. Por ejemplo, se puede demostrar que, independientemente de si un modelo de ZF V satisface la hipótesis del continuo o la axioma de elección, el modelo interno L construido en el interior del modelo original satisfará tanto la hipótesis del continuo y el axioma de elección. Así, la suposición de que ZF es consistente (tiene cualquier modelo en absoluto) implica que ZF junto con estos dos principios es consistente.

El estudio de los modelos internos es común en el estudio de la determinación y grandes cardenales, especialmente cuando se considera axiomas tales como el axioma de la determinación que contradice el axioma de elección. Incluso si un modelo fijo de la teoría de conjuntos satisface el axioma de elección, es posible que un modelo interno no pueda cumplir con el axioma de elección. Por ejemplo, la existencia de suficiente grandes cardinales implica que hay un modelo interno satisface el axioma de la determinación (y por lo tanto no satisface el axioma de elección).

Las grandes cardenales

Una gran cardinal es un número cardinal con una propiedad adicional. Muchas de estas propiedades son estudiadas, incluyendo cardenales inaccesibles, cardenales medibles, y muchos más. Estas propiedades lo general implican el número cardinal debe ser muy grande, con la existencia de un cardenal con la propiedad especificada indemostrable en Zermelo-Fraenkel la teoría de conjuntos.

Determinación

Determinación se refiere al hecho de que, bajo supuestos apropiados, ciertos juegos de dos jugadores de la información perfecta se determinan desde el principio en el sentido de que un jugador debe tener una estrategia ganadora. La existencia de estas estrategias tiene consecuencias importantes en la teoría de conjuntos descriptiva, como el supuesto de que una clase más amplia de juegos se determina a menudo implica que una clase más amplia de conjuntos tendrá una propiedad topológica. La axioma de determinación (EA) es un importante objeto de estudio; si bien es incompatible con el axioma de elección, AD implica que todos los subconjuntos de la recta real se comportan bien (en particular, medibles y con la propiedad de conjunto perfecto). AD se puede utilizar para probar que el Grados wadge tienen una estructura elegante.

Obligar

Paul Cohen inventó obligando al buscar un modelo de ZFC en la que el hipótesis del continuo falla. Forzar adjunta a algún determinado modelo de la teoría de conjuntos conjuntos adicionales con el fin de crear un modelo más grande con propiedades determinadas por la construcción y el modelo original. Por ejemplo, la construcción de Cohen colinda subconjuntos adicionales de los números naturales sin cambiar ninguno de los números cardinales del modelo original. Forzar es también uno de los dos métodos para probar relativa consistencia por métodos finitistas, siendo el otro método Modelos de Boole de valor.

Invariantes cardinales

Un invariante cardinal es una propiedad de la recta real medido por un número cardinal. Por ejemplo, una invariante bien estudiado es la cardinalidad más pequeña de una colección de escasos conjuntos de números reales cuya unión es toda la recta real. Estos son invariantes en el sentido de que cualquiera de los dos modelos isomórficos de la teoría de conjuntos deben dar el mismo cardinal para cada invariante. Muchos invariantes cardinales se han estudiado, y las relaciones entre ellos son a menudo complejas y relacionadas con los axiomas de la teoría de conjuntos.

Topología conjuntista

Set-teóricos estudios de topología preguntas de topología general que son de teoría de conjuntos en la naturaleza o que requieren métodos de la teoría de conjuntos avanzados para su solución. Muchos de estos teoremas son independientes de ZFC, requiriendo axiomas más fuertes para su prueba. Un famoso problema es la espacio normal Moore pregunta, una pregunta en la topología general de que ha sido objeto de intensa investigación. La respuesta a la pregunta del espacio normal de Moore fue finalmente resultó ser independiente de ZFC.

Las objeciones a la teoría de conjuntos

Desde su creación, se han producido algunos matemáticos que tienen objetado el uso de la teoría de conjuntos como base para las matemáticas, afirmando que es sólo un juego que incluye elementos de fantasía. Errett Obispo desestimó la teoría de conjuntos como " Dios matemáticas 's, que debemos dejar que Dios haga. " También Ludwig Wittgenstein cuestionó especialmente el manejo de infinitos, que se refiere también ZF. Puntos de vista de Wittgenstein sobre fundamentos de las matemáticas han sido criticadas por Paul Bernays, y estrechamente investigados por Crispin Wright, entre otros.

La objeción más frecuente a la teoría de conjuntos es el visión constructivista de que las matemáticas es poco relacionada con la computación y que la teoría de conjuntos ingenua se formalizó con la adición de elementos noncomputational.

Topos ha sido propuesta como una alternativa a la teoría de conjuntos axiomático tradicional. Topos se puede utilizar para interpretar varias alternativas para la teoría de conjuntos tales como constructivismo, la teoría de conjuntos finitos, y la teoría de conjuntos computable.