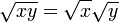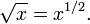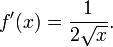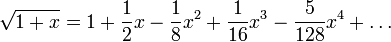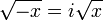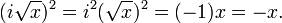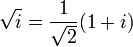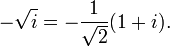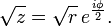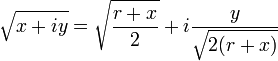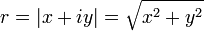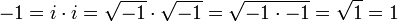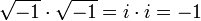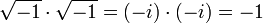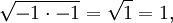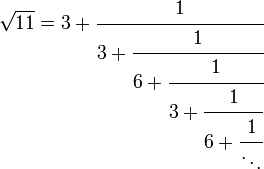Raíz cuadrada

En matemáticas , una raíz cuadrada (√) de un número x es un número r tal que r ² = x, o en palabras, un número r cuya cuadrada (el resultado de multiplicar el número por sí mismo) es x. Cada no negativo número real x tiene una raíz cuadrada no negativa única, llamada la raíz cuadrada principal e denotado con un símbolo radical como √ x. Por ejemplo, el director de la raíz cuadrada de 9 es 3, que se denota √ 9 = 3, porque 3 ² = 3 x 3 = 9.

Las raíces cuadradas a menudo surgen en la resolución de ecuaciones de segundo grado , o ecuaciones de la forma ax ² + bx + c = 0, debido a la variable x está al cuadrado.

Cada número positivo x tiene dos raíces cuadradas. Uno de ellos es √ x, que es positivo, y los otros -√ x, que es negativo. Juntos, estos dos raíces se denotan ± √ x. Las raíces cuadradas de números negativos pueden ser discutidas en el marco de los números complejos . Las raíces cuadradas de los objetos que no son números también se pueden definir.

Las raíces cuadradas de números enteros que no son cuadrados perfectos son siempre los números irracionales : los números no expresables como relación de dos números enteros. Por ejemplo, √ 2 no se puede escribir exactamente como m / n, donde n y m son números enteros. Sin embargo, es exactamente la longitud de la diagonal de un cuadrado con una longitud de lado 1. Esto ha sido conocido desde la antigüedad, con el descubrimiento de que √ 2 es irracional atribuido a Hiparco, discípulo de Pitágoras . (Ver raíz cuadrada de 2 para las pruebas de la irracionalidad de este número.)

Propiedades

La gráfica de la función f (x) = √ x, formado por medio de una parábola con la vertical directriz.

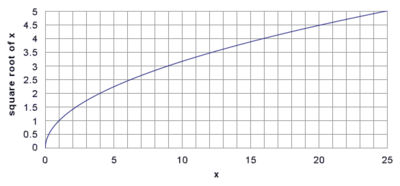
El director de la función de raíz cuadrada f (x) = √ x (por lo general sólo se refiere como la "función de raíz cuadrada") es una función que mapea el conjunto de no negativo números reales R ⁺ ∪ {0} sobre sí mismo, y, al igual que todas las funciones, siempre devuelve un valor único. La función de raíz cuadrada también asigna números racionales en números algebraicos (un superconjunto de los números racionales); √ x es racional si y sólo si x es un número racional que puede ser representada como una proporción de dos cuadrados perfectos. En geométricas términos, la función de raíz cuadrada asigna el área de un cuadrado a su longitud lateral.

• Para todos los números reales x,

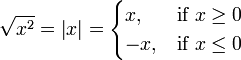(Ver valor absoluto )

• Para todos los números reales no negativos x e y,

y

• La función raíz cuadrada es continua para todo x no negativos y diferenciable para todo x positivos. Su derivado está dada por

• La serie de Taylor de √ 1 + x sobre x = 0 converge para | x | <1 y se da por

Cálculo

Existen muchos métodos para calcular raíces cuadradas hoy, algunos destinados a ser hecho a mano y algo destinado a ser hecho por la máquina.

Muchas, pero no todas las calculadoras de bolsillo tienen una clave raíz cuadrada. Computadora hojas de cálculo y otros software también se utilizan con frecuencia para calcular raíces cuadradas. Los programas informáticos suelen implementar buenas rutinas para calcular la función exponencial y el logaritmo natural o logaritmo , y luego calcular la raíz cuadrada de x utilizando la identidad

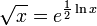o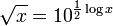

La misma identidad se explota al calcular raíces cuadradas con tablas de logaritmos o reglas de cálculo.

El método más común para el cálculo de la raíz cuadrada a mano es conocida como la " . Método babilónico "Se trata de un simple algoritmo, lo que resulta en un número más cercano a la raíz cuadrada real cada vez que se repite Para encontrar r, la raíz cuadrada de un número real x.:

1. Comience con un valor r comienzo positivo arbitrario (cuanto más cerca de la raíz cuadrada de x, mejor).
2. Reemplazar r por el promedio entre r y x / r. (Es suficiente para tener un valor aproximado de la media, no demasiado cerca del valor anterior de r y x / r con el fin de garantizar convergencia.)
3. Repita el paso 2 hasta que r y x / r están tan cerca como se desee.

Las más conocidas complejidad de tiempo para calcular una raíz cuadrada con n dígitos de precisión es el mismo que para la multiplicación de dos números de n -dígitos.

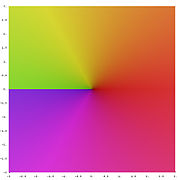
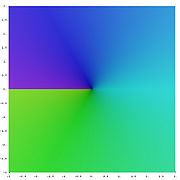
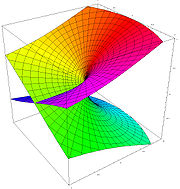
Las raíces cuadradas de números negativos y complejos

Raíz cuadrada Complejo

En segundo lugar de la hoja de la raíz cuadrada compleja

El uso de la superficie de Riemann de la raíz cuadrada, se puede ver cómo las dos hojas encajan

El cuadrado de cualquier número positivo o negativo es positivo, y el cuadrado de 0 es 0. Por lo tanto, no hay ningún número negativo puede tener una raíz cuadrada real. Sin embargo, es posible trabajar con un conjunto más amplio de números, llamados los números complejos , que contiene soluciones a la raíz cuadrada de un número negativo. Esto se realiza mediante la introducción de un nuevo número, denotado por i (j veces, especialmente en el contexto de electricidad) y llamó a la unidad imaginaria , que se define de tal manera que i ² = -1. Utilizando esta notación, podemos pensar en i como la raíz cuadrada de -1, de notar que también tenemos (- i) ² = i ² = -1 y así - i es también una raíz cuadrada de -1. De manera similar a los números reales, decimos que el director de la raíz cuadrada de -1 es i, o, más generalmente, si x es cualquier número positivo, entonces la raíz cuadrada principal de - x es

porque

Por el argumento dado anteriormente, puedo ser ni positivo ni negativo. Esto crea un problema: para el número complejo z, no podemos definir √ z para ser la raíz cuadrada "positiva" de z.

Por cada número complejo z no cero existen exactamente dos números w tal que w ² = z. Por ejemplo, las raíces cuadradas de i son:

y

La definición habitual de √ z es mediante la introducción de la siguiente rama cortada: si z = r e ^{i φ} está representado en coordenadas polares con -π <φ ≤ π, entonces nos fijamos el valor principal a

Definido de esta manera, la función de raíz cuadrada es holomorfa en todas partes menos en los números reales no positivos (donde no es aún continua). La anterior serie de Taylor para √ 1 + x sigue siendo válido para números complejos x con | x | <1.

Cuando el número es en forma rectangular la siguiente fórmula se puede utilizar para el valor principal:

donde

es el valor absoluto o el módulo del número complejo, a menos que x = - r e y = 0. Obsérvese que el signo de la parte imaginaria de la raíz es el mismo que el signo de la parte imaginaria del número original. La parte real del valor principal es siempre no negativo.

Tenga en cuenta que debido a la naturaleza discontinua de la función de raíz cuadrada en el plano complejo, la ley √ zw = √ √ z w es, en general, no es cierto. (Equivalente, el problema se produce a causa de la libertad en la elección de la rama La rama elegida puede o no dar el igualdad;. De hecho, la elección de la rama de la raíz cuadrada no tiene por qué contener el valor de z √ √ w en absoluto , lo que lleva al fracaso de la igualdad. Un problema similar se presenta con la . logaritmo complejo y el registro de relación z + log w = log (zw)) asumiendo erróneamente esta ley subyace varias "pruebas" defectuosas, por ejemplo el siguiente uno que muestra que -1 = 1:

La tercera igualdad no puede justificarse (ver la prueba no válido), sin embargo, puede ser ajustado para ser verdad si (1) la libertad de permiso en la elección de la rama por que ya no requiere la raíz cuadrada principal (definido en el principio del artículo) implícita en la notación √ y (2 ) elige la rama de la raíz cuadrada con el fin de excluir el valor 1. El lado izquierdo se convierte ya sea

si la rama incluye + io

si la rama incluye - i, mientras que el lado derecho se convierte en

de nuevo por la elección de la rama.

Las raíces cuadradas de matrices y los operadores

Si A es una matriz u operador definida positiva, entonces no existe precisamente una matriz definida positiva u operador B con B ² = A; entonces definimos √ A = B.

Más en general, a cada matriz normal o el operador A no existen operadores normales B tal que B ² = A. En general, hay varios dichos operadores B para cada A y la función de raíz cuadrada no se pueden definir para los operadores normales de una manera satisfactoria. Operadores definidos positivos son similares a los números reales positivos, y los operadores normales son similares a los números complejos.

Raíces cuadradas principales de los primeros 20 números enteros positivos

Como fracciones decimales no periódicas

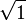
		1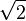
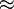
		1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462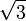
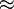
		1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909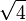
		2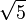
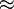
		2,2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638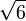
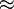
		2,4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457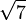
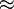
		2,6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230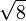
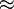
		2,8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924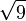
		3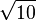
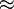
		3,1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639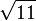
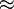
		3,3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609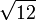
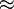
		3,4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818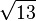
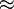
		3,6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293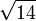
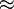
		3,7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307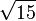
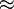
		3,8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937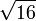
		4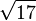
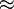
		4,1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338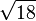
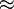
		4,2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386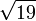
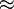
		4,3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203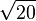
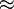
		4,4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276

Como fracciones continuas periódicas

Uno de los resultados más interesantes del estudio de números irracionales como fracciones continuas se obtuvo por Joseph Louis Lagrange circa 1780. Lagrange encontró que la raíz cuadrada de cualquier número entero positivo no cuadrado puede ser representada por una periódico fracción continua. Es decir, en el que un cierto patrón de dígitos se produce una y otra vez en los denominadores (ver ejemplo debajo de la tabla). En cierto sentido, estas raíces cuadradas son los números irracionales muy simples, ya que pueden ser representados con un simple patrón de repetición de dígitos.

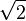
		[1; 2, 2, ...]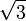
		[1; 1, 2, 1, 2, ...]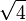
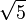
		[2; 4, 4, ...]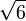
		[2; 2, 4, 2, 4, ...]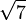
		[2; 1, 1, 1, 4, 1, 1, 1, 4, ...]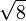
		[2; 1, 4, 1, 4, ...]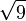
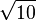
		[3; 6, 6, ...]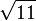
		[3; 3, 6, 3, 6, ...]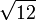
		[3; 2, 6, 2, 6, ...]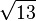
		[3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6, ...]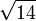
		[3; 1, 2, 1, 6, 1, 2, 1, 6, ...]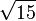
		[3; 1, 6, 1, 6, ...]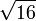
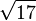
		[4; 8, 8, ...]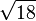
		[4; 4, 8, 4, 8, ...]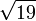
		[4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8, ...]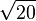
		[4; 2, 8, 2, 8, ...]

La notación de corchetes utilizado anteriormente es una especie de taquigrafía matemática para ahorrar espacio. Escrito en más notación tradicional de la simple fracción continua de la raíz cuadrada de 11 - [3; 3, 6, 3, 6, ...] - se parece a esto:

donde el patrón de dos dígitos {3, 6} se repite una y otra y otra vez en los denominadores parciales.

Construcción geométrica de la raíz cuadrada

A raíz cuadrada se puede construir con un compás y una regla. En sus Elementos , Euclides (fl. 300 aC) dio a la construcción de la media geométrica de dos cantidades en dos lugares diferentes: Proposición II.14 y Proposición VI.13. Dado que la media geométrica de a y b es √ ab, se puede construir un √ simplemente tomando b = 1.

La construcción también está dada por Descartes en su La Géométrie, ver figura 2 en página 2. Sin embargo, Descartes no hizo ninguna pretensión de originalidad y su audiencia habría sido bastante familiarizado con Euclides.

Otro método de construcción geométrica utiliza correctas triángulos y inducción: √ 1 puede, por supuesto, ser construida, y una vez √ x se ha construido, el triángulo rectángulo con 1 y √ x por sus piernas tiene un hipotenusa de √ x + 1.

Historia

La Papiro matemático de Rhind es una copia de 1650 aC de una obra aún más temprano y nos muestra cómo los egipcios extraen raíces cuadradas.

En la antigua India , el conocimiento de los aspectos teóricos y aplicados de la raíz cuadrada y la plaza fue al menos tan antigua como la Sulba Sutras, fechada alrededor 800-500 aC (posiblemente mucho antes). Un método para encontrar muy buenas aproximaciones a las raíces cuadradas de 2 y 3 se dan en la Baudhayana Sulba Sutra. Aryabhata en el Aryabhatiya (sección 2.4), ha dado un método para encontrar la raíz cuadrada de números que tienen muchos dígitos.

DE Smith en Historia de las Matemáticas, dice, acerca de la situación existente en Europa: "En Europa estos métodos (para averiguar el cuadrado y raíz cuadrada) no comparecer ante Cataneo (1546). Él dio el método de Aryabhata para determinar la raíz cuadrada ".