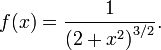La distribución t de Student
Sabías ...
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?
La función de densidad de probabilidad 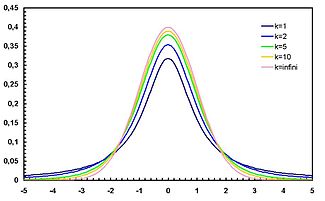 | |
Función de distribución acumulativa 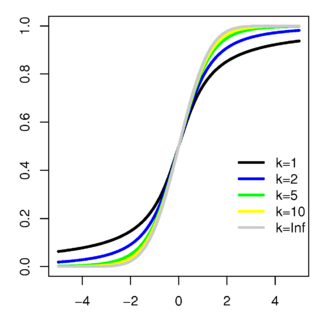 | |
| Parámetros | 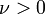 grados de libertad ( verdadero ) grados de libertad ( verdadero ) |
|---|---|
| Apoyo | 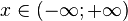 |
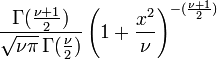 | |
| CDF | ![\ Begin {matriz} \ frac {1} {2} + x \ Gamma \ dejó (\ frac {\ nu + 1} {2} \ right) \ cdot \\ [0.5em] \ frac {\, _ 2F_1 \ left (\ frac {1} {2}, \ frac {\ nu + 1} {2}; \ frac {3} {2}; - \ frac {x ^ 2} {\ nu} \ right)} {\ sqrt {\ pi nu \} \, \ Gamma (\ frac {\ nu} {2})} \ end {matriz}](../../images/122/12276.png) donde 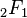 es el función hipergeométrica es el función hipergeométrica |
| Significar | 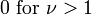 , De otro modo indefinido , De otro modo indefinido |
| Mediana | 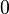 |
| Modo | 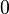 |
| Desacuerdo | 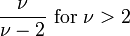 , De otro modo indefinido , De otro modo indefinido |
| Oblicuidad | 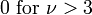 |
| Ex. curtosis | 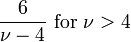 |
| Entropía | ![\ Begin {matriz} \ frac {\ nu + 1} {2} \ left [\ psi (\ frac {1+ \ nu} {2}) - \ psi (\ frac {\ nu} {2}) \ right ] \\ [0.5em] + \ log {\ left [\ sqrt {\ nu} B (\ frac {\ nu} {2}, \ frac {1} {2}) \ right]} \ end {matriz}](../../images/122/12283.png)
|
| MGF | (No definido) |
De la t de Student distribución t (o también t -distribución), en probabilidad y estadística , es una distribución de probabilidad que se plantea en el problema de la estimación de la media de una distribución normal cuando la población tamaño de la muestra es pequeño. Es la base de la popular t de Student pruebas para la significación estadística de la diferencia entre dos muestras medios , y para intervalos de confianza para la diferencia entre dos medias de población. Distribución t de Student es un caso especial de la distribución hiperbólica generalizada.
La derivación de la distribución t t se publicó por primera vez en 1908 por William Sealy Gosset, mientras trabajaba en un Fábrica de cerveza Guinness en Dublín . Se le prohibió publicar bajo su propio nombre, por lo que el documento ha sido escrito bajo el seudónimo de Student. El t-test y la teoría asociada se hizo muy conocido a través de la obra de RA Fisher, quien llamó a la distribución "de Student".
Distribución de Student surge cuando (como en el trabajo estadístico casi toda práctica) la población desviación estándar es desconocida y tiene que estimarse a partir de los datos. Problemas de libros de texto que tratan a la desviación estándar como si se supiera son de dos tipos: (1) aquellos en los que el tamaño de la muestra es tan grande que uno puede tratar una estimación basada en datos de la varianza como si fuera cierta, y (2) aquellos que ilustran el razonamiento matemático, en el que el problema de la estimación de la desviación estándar se ignora temporalmente porque ese no es el punto de que el autor o el instructor está explicando a continuación.
¿Por qué utilizar t -distribución del Estudiante
Los intervalos de confianza y pruebas de hipótesis se basan en t -distribución de Student para hacer frente a la incertidumbre resultante de la estimación de la desviación estándar de una muestra, mientras que si la desviación estándar de la población eran conocidos, una distribución normal sería utilizado.
Cómo -distribución t de Student se produce
Supongamos que X 1, ..., X n son independientes variables aleatorias que normalmente se distribuyen con μ valor esperado y varianza σ 2. Dejar
sea la media de la muestra, y
ser la varianza de la muestra. Se muestra fácilmente que la cantidad
se distribuye normalmente con media 0 y varianza 1, ya que la media de la muestra 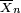 se distribuye normalmente con media
se distribuye normalmente con media 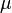 y el error estándar
y el error estándar 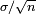 .
.
Gosset estudió una relacionada cantidad pivotal,
que difiere de Z en que la desviación estándar exacta  se sustituye por la variable aleatoria
se sustituye por la variable aleatoria 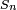 . Técnicamente,
. Técnicamente, 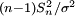 tiene un
tiene un 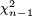 distribución por El teorema de Cochran. El trabajo de Gosset demostró que T tiene la la función de densidad de probabilidad
distribución por El teorema de Cochran. El trabajo de Gosset demostró que T tiene la la función de densidad de probabilidad
con ν igual a n - 1 y donde Γ es la Función gamma.
Esto también puede ser escrito como
donde B es la Función Beta.
La distribución de T ahora se llama el t -distribución. El ν parámetro se denomina el número de grados de libertad. La distribución depende de ν, pero no μ o σ; la falta de dependencia de μ y σ es lo que hace el t -distribución importante tanto en la teoría y la práctica.
Los momentos de la distribución t son
Cabe señalar que el término para 0 <k <ν, k incluso, puede simplificarse utilizando las propiedades de la Función Gamma a
Los intervalos de confianza derivados de la t de Student -distribución
Supongamos que el número A se elegirán de manera que
cuando T tiene una distribución t t con n - 1 grados de libertad. Este es el mismo que
por lo que A es el "percentil 95" de esta distribución de probabilidad, o 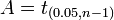 . Entonces
. Entonces
y esto es equivalente a
Por lo tanto el intervalo cuyos extremos están
es un 90 por ciento intervalo de confianza para μ. Por lo tanto, si nos encontramos con la media de un conjunto de observaciones que razonablemente podemos esperar tener una distribución normal, podemos utilizar el t -distribución examinar si los límites de confianza en que media incluyen algún valor predicho teóricamente - tales como el valor predicho en un hipótesis nula.
Este es el resultado que se utiliza en la t de Student pruebas : ya que la diferencia entre las medias de muestras de dos distribuciones normales es en sí mismo una distribución normal, el t -distribución se puede utilizar para comprobar si esta diferencia puede razonablemente suponerse que es cero .
Si los datos se distribuyen normalmente, el de un solo lado (1 - a) Límite -Superior confianza (UCL) de la media, se puede calcular mediante la siguiente ecuación:
El UCL resultante será el mayor valor promedio que se producirá durante un intervalo de confianza y tamaño de la población dada. En otras palabras, 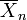 siendo la media del conjunto de observaciones, la probabilidad de que la media de la distribución es inferior a
siendo la media del conjunto de observaciones, la probabilidad de que la media de la distribución es inferior a 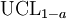 es igual al nivel de confianza
es igual al nivel de confianza 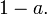
Un número de otras estadísticas puede ser demostrado tener camisetas -distributions para muestras de tamaño moderado bajo hipótesis nulas que son de interés, de manera que el t -Distribución forma la base para las pruebas de significación en otras situaciones, así como al examinar las diferencias entre medias. Por ejemplo, la distribución de Coeficiente de correlación de Spearman, rho, en el caso nulo (correlación cero) es bien aproximada por la distribución t para tamaños de muestra por encima de unos 20.
Ver intervalo de predicción para otro ejemplo de la utilización de esta distribución.
Integral de la función de densidad de probabilidad y p-valor del Estudiante
La función 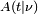 es la integral de la función de densidad de probabilidad de Student, ƒ (t) entre - t y t. Por lo tanto, da la probabilidad de que un valor de t menor que la calculada a partir de los datos observados se produciría por casualidad. Por lo tanto, la función de
es la integral de la función de densidad de probabilidad de Student, ƒ (t) entre - t y t. Por lo tanto, da la probabilidad de que un valor de t menor que la calculada a partir de los datos observados se produciría por casualidad. Por lo tanto, la función de 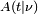 se puede utilizar cuando se prueba si la diferencia entre las medias de dos conjuntos de datos es estadísticamente significativa, mediante el cálculo del valor correspondiente de t y la probabilidad de su ocurrencia si los dos conjuntos de datos se extrajeron de la misma población. Esto se utiliza en una variedad de situaciones, en particular en t-pruebas . Para la estadística t, con
se puede utilizar cuando se prueba si la diferencia entre las medias de dos conjuntos de datos es estadísticamente significativa, mediante el cálculo del valor correspondiente de t y la probabilidad de su ocurrencia si los dos conjuntos de datos se extrajeron de la misma población. Esto se utiliza en una variedad de situaciones, en particular en t-pruebas . Para la estadística t, con  grados de libertad,
grados de libertad, 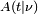 es la probabilidad de que t sería menor que el valor observado si los dos medios fueron los mismos (siempre que la media más pequeña se resta de la más grande, de manera que t> 0). Se define para t real mediante la siguiente fórmula:
es la probabilidad de que t sería menor que el valor observado si los dos medios fueron los mismos (siempre que la media más pequeña se resta de la más grande, de manera que t> 0). Se define para t real mediante la siguiente fórmula:
donde B es la Función Beta. Para t> 0, hay una relación con el regularizado función beta incompleta I x (a, b) como sigue:
La probabilidad de que un valor de la estadística t mayor o igual al observado que sucedería por casualidad, si los dos conjuntos de datos se extrajeron de la misma población, está dada por
Además teoría
Resultado de Gosset puede afirmar de manera más general. (Véase, por ejemplo, Hogg y Craig, Secciones 4.4 y 4.8.) Deje Z tener una distribución normal con media 0 y varianza 1. Sea V una distribución chi-cuadrado con ν grados de libertad. Además suponen que Z y V son independiente (véase El teorema de Cochran). Entonces la relación
tiene una distribución t t con ν grados de libertad.
Para una distribución t t con ν grados de libertad, la valor esperado es 0, y su varianza es ν / (ν - 2) si ν> 2. La asimetría es 0 y el curtosis es 6 / (ν - 4) si ν> 4.
La función de distribución acumulada está dada por una función beta incompleta,
con
El t -Distribución está relacionado con el F-distribución de la siguiente manera: el cuadrado de un valor de t con ν grados de libertad se distribuye de la F con 1 y ν grados de libertad.
La forma general de la función de densidad de probabilidad de la distribución t t se asemeja a la forma de campana de una distribución normal con media variable de 0 y varianza 1, excepto que es un poco más bajo y ancho. Como el número de grados de libertad crece, la distribución t t se aproxima a la distribución normal con media 0 y varianza 1.
Las siguientes imágenes muestran la densidad de la distribución t t para valores de ν creciente. La distribución normal se muestra como una línea azul para la comparación .; Tenga en cuenta que la distribución t t (línea roja) se acerca más a la distribución normal a medida que aumenta ν. Para ν = 30 t la distribución t es casi la misma que la distribución normal.
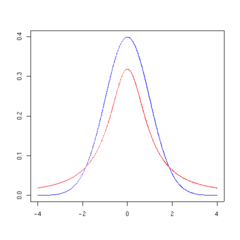 | 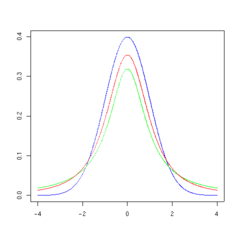 | 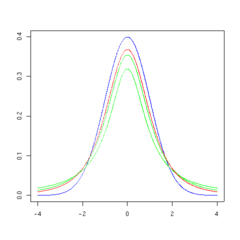 |
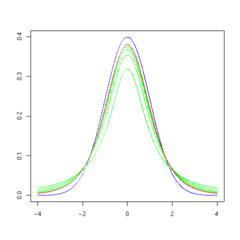 | 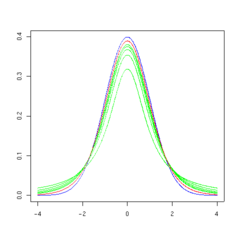 | 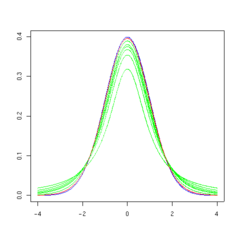 |
Tabla de valores seleccionados
La siguiente tabla muestra algunos valores seleccionados para las camisetas, las distribuciones con grados de libertad ν para una serie de intervalos de confianza de un solo lado. Para un ejemplo de cómo leer esta tabla, tomar la cuarta fila, que comienza con 4; eso significa ν, el número de grados de libertad, es de 4 (y si se trata, como el anterior, con n valores con una suma fija, n = 5). Tome la quinta entrada, en la columna 95%. El valor de esa entrada es "2,132". Entonces la probabilidad de que T es menor que 2,132 es 95% o 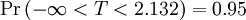 ; la entrada no significa (como puede ser que con otras distribuciones) que
; la entrada no significa (como puede ser que con otras distribuciones) que 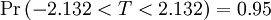 .
.
De hecho, por la simetría de la distribución,
- Pr (T <-2,132) = 1 - Pr (T> -2,132) = 1-0,95 = 0,05,
y entonces
- Pr (-2,132 <T <2,132) = 1 - 2 (0,05) = 0,9.
Tenga en cuenta que la última fila también da puntos críticos: un t -distribución con infinitamente muchos grados de libertad es una distribución normal. (Ver más abajo: distribuciones relacionadas).
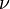 | 75% | 80% | 85% | 90% | 95% | 97,5% | 99% | 99,5% | 99,75% | 99,9% | 99,95% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1,000 | 1,376 | 1,963 | 3,078 | 6,314 | 12.71 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0,816 | 1,061 | 1,386 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | 14.09 | 22.33 | 31.60 |
| 3 | 0,765 | 0,978 | 1,250 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | 7,453 | 10.21 | 12.92 |
| 4 | 0,741 | 0,941 | 1,190 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | 5,598 | 7.173 | 8,610 |
| 5 | 0,727 | 0,920 | 1,156 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | 4,773 | 5,893 | 6,869 |
| 6 | 0,718 | 0,906 | 1,134 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | 4,317 | 5,208 | 5,959 |
| 7 | 0,711 | 0,896 | 1,119 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | 4,029 | 4,785 | 5,408 |
| 8 | 0,706 | 0,889 | 1,108 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | 3,833 | 4,501 | 5,041 |
| 9 | 0,703 | 0,883 | 1,100 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | 3,690 | 4,297 | 4,781 |
| 10 | 0,700 | 0,879 | 1,093 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | 3,581 | 4.144 | 4,587 |
| 11 | 0,697 | 0,876 | 1,088 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 3,497 | 4,025 | 4,437 |
| 12 | 0,695 | 0,873 | 1,083 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 3,428 | 3,930 | 4,318 |
| 13 | 0,694 | 0,870 | 1,079 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | 3,372 | 3,852 | 4,221 |
| 14 | 0,692 | 0,868 | 1,076 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 3,326 | 3,787 | 4,140 |
| 15 | 0,691 | 0,866 | 1,074 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | 3,286 | 3,733 | 4,073 |
| 16 | 0,690 | 0,865 | 1,071 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 | 3,252 | 3,686 | 4,015 |
| 17 | 0,689 | 0,863 | 1,069 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 | 3,222 | 3,646 | 3,965 |
| 18 | 0,688 | 0,862 | 1,067 | 1,330 | 1,734 | 2.101 | 2,552 | 2,878 | 3,197 | 3,610 | 3,922 |
| 19 | 0,688 | 0,861 | 1,066 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | 3,174 | 3,579 | 3,883 |
| 20 | 0,687 | 0,860 | 1,064 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | 3,153 | 3,552 | 3,850 |
| 21 | 0,686 | 0,859 | 1,063 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 | 3,135 | 3,527 | 3,819 |
| 22 | 0,686 | 0,858 | 1,061 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 | 3,119 | 3,505 | 3,792 |
| 23 | 0,685 | 0,858 | 1,060 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 | 3,104 | 3,485 | 3,767 |
| 24 | 0,685 | 0,857 | 1,059 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 | 3,091 | 3,467 | 3,745 |
| 25 | 0,684 | 0,856 | 1,058 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 | 3,078 | 3,450 | 3,725 |
| 26 | 0,684 | 0,856 | 1,058 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 | 3,067 | 3,435 | 3,707 |
| 27 | 0,684 | 0,855 | 1,057 | 1,314 | 1,703 | 2,052 | 2,473 | 2,771 | 3,057 | 3,421 | 3,690 |
| 28 | 0,683 | 0,855 | 1,056 | 1,313 | 1,701 | 2,048 | 2,467 | 2,763 | 3,047 | 3,408 | 3,674 |
| 29 | 0,683 | 0,854 | 1,055 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 | 3,038 | 3,396 | 3,659 |
| 30 | 0,683 | 0,854 | 1,055 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 | 3,030 | 3,385 | 3,646 |
| 40 | 0,681 | 0,851 | 1,050 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 | 2,971 | 3,307 | 3,551 |
| 50 | 0,679 | 0,849 | 1,047 | 1,299 | 1,676 | 2,009 | 2,403 | 2,678 | 2,937 | 3,261 | 3,496 |
| 60 | 0,679 | 0,848 | 1,045 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 | 2,915 | 3,232 | 3,460 |
| 80 | 0,678 | 0,846 | 1,043 | 1,292 | 1,664 | 1,990 | 2,374 | 2,639 | 2,887 | 3,195 | 3,416 |
| 100 | 0,677 | 0,845 | 1,042 | 1,290 | 1,660 | 1,984 | 2,364 | 2,626 | 2,871 | 3,174 | 3,390 |
| 120 | 0,677 | 0,845 | 1,041 | 1,289 | 1,658 | 1,980 | 2,358 | 2,617 | 2,860 | 3,160 | 3,373 |
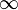 | 0,674 | 0,842 | 1,036 | 1,282 | 1,645 | 1,960 | 2,326 | 2,576 | 2,807 | 3,090 | 3,291 |
Ver también t-mesa .
El número al comienzo de cada fila en la tabla anterior es ν que se ha definido anteriormente como n - 1. El porcentaje a lo largo de la parte superior es 100% (1 - α). Los números en el cuerpo principal de la tabla son t α, ν. Si una cantidad T se distribuye de la distribución t de Student con grados ν de la libertad, entonces hay una probabilidad 1 -. Α que T será menor que t α, ν (Calculado como para una prueba de una cola o unilateral como oposición a una dos colas de prueba.)
Por ejemplo, dada una muestra con una varianza de la muestra 2 y media de la muestra de 10, tomada de un conjunto de muestra de 11 (10 grados de libertad), utilizando la fórmula
Podemos determinar que al 90% de confianza, tenemos una verdadera media se encuentra por debajo
(En otras palabras, en promedio, 90% de las veces que un umbral superior se calcula por este método, la media real se encuentra por debajo de este umbral superior.) Y, todavía en confianza del 90%, tenemos una media verdadera miente sobre
(En otras palabras, en promedio, 90% de las veces que un umbral inferior se calcula mediante este método, la media real se encuentra por encima de este umbral inferior.) Así que al 80% de confianza, tenemos una verdadera media se extiende entre
(En otras palabras, en promedio, 80% de las veces que los umbrales superior e inferior se calculan por este método, la media verdadera es a la vez por debajo del umbral superior y por encima del umbral inferior. Esto no es lo mismo que decir que hay una probabilidad del 80% que la media real se encuentra entre un par particular de los umbrales superior e inferior que se han calculado por este método - ver intervalo de confianza y falacia del fiscal.)
Para obtener información sobre la función de distribución acumulada inversa ver Función cuantil.
Casos especiales
Ciertos valores de ν dan una forma especialmente sencilla.
ν = 1
Función de distribución:
Función de densidad:
Ver Distribución de Cauchy
ν = 2
Función de distribución:
Función de densidad:
Modelado paramétrico Robusto
El t -Distribución se utiliza a menudo como una alternativa a la distribución normal como un modelo para los datos. Es frecuente que los datos reales tienen colas más pesadas que la distribución normal permite. El enfoque clásico fue identificar valores atípicos y excluir o restar importancia ellos de alguna manera. Sin embargo, no siempre es fácil de identificar valores atípicos (especialmente en dimensiones de altura), y el t -distribución es una elección natural de modelo para este tipo de datos y proporciona un enfoque paramétrico para estadística robusta.
Lange et al exploró el uso de la t -Distribución para el modelado de datos robusta de cola pesados en una variedad de contextos. Una cuenta Bayesiano se puede encontrar en Gelman et al. Los grados de libertad parámetro controla la curtosis de la distribución y se correlaciona con el parámetro de escala. La probabilidad puede tener máximos locales múltiples y, como tal, a menudo es necesario fijar los grados de libertad en un valor bastante bajo y estimar los otros parámetros Tomando esto como dado. Algunos autores informan que los valores entre 3 y 9 son a menudo buenas opciones. Venables y Ripley sugieren que un valor de 5 a menudo es una buena opción.
Distribuciones Relacionados
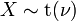 tiene una distribución t t si
tiene una distribución t t si 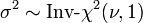 tiene un escalado microscopios invertidos χ 2 distribución y
tiene un escalado microscopios invertidos χ 2 distribución y 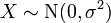 tiene una distribución normal .
tiene una distribución normal . 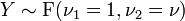 tiene una F -distribución si
tiene una F -distribución si 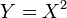 y
y 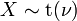 tiene t -distribución de Student.
tiene t -distribución de Student. 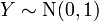 tiene una distribución normal como
tiene una distribución normal como 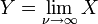 donde
donde 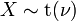 .
. 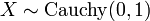 tiene un Distribución de Cauchy si
tiene un Distribución de Cauchy si 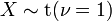 .
.


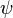 : función digamma,
: función digamma, 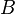 : función beta
: función beta 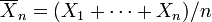
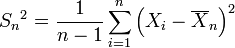
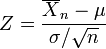
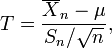
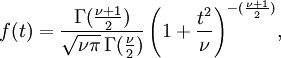
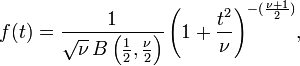


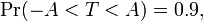
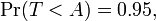
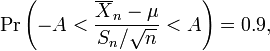

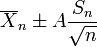
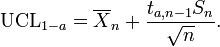
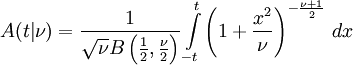
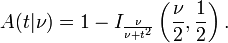
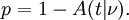
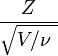
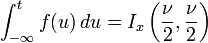
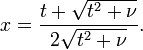
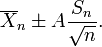
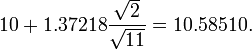
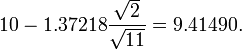
![10 \ pm1.37218 \ frac {\ sqrt {2}} {\ sqrt {11}} = [9.41490, 10.58510].](../../images/123/12345.png)
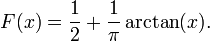
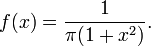
![F (x) = \ frac {1} {2} \ left [1 + \ frac {x} {\ sqrt {2 + x ^ 2}} \ right].](../../images/123/12348.png)