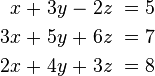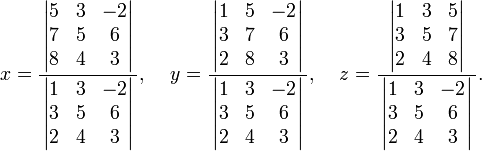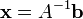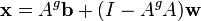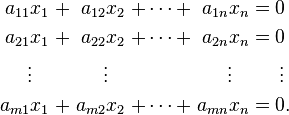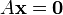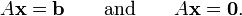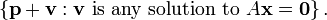Sistema de ecuaciones lineales
Antecedentes de las escuelas de Wikipedia
SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Infantil SOS es la mayor donación de caridad del mundo niños huérfanos y abandonados de la oportunidad de la vida familiar.
En matemáticas , un sistema de ecuaciones lineales (o sistema lineal) es un conjunto de ecuaciones lineales que implica el mismo conjunto de variables. Por ejemplo,
es un sistema de tres ecuaciones con las tres variables x, y, z. Una solución a un sistema lineal es una asignación de números a las variables tales que todas las ecuaciones se satisfacen simultáneamente. La solución para el sistema anterior está dada por
ya que hace que las tres ecuaciones válidas.
En matemáticas, la teoría de sistemas lineales es la base y una parte fundamental del álgebra lineal , un tema que se utiliza en la mayor parte de la matemática moderna. Computacional algoritmos para encontrar las soluciones son una parte importante de álgebra lineal numérica, y desempeñar un papel destacado en la ingeniería , la física , la química , la informática y la economía . La sistema de ecuaciones no lineales puede ser a menudo aproximada por un sistema lineal (ver linealización), una técnica útil al realizar una modelo matemático o simulación por ordenador de un sistema relativamente complejo.
Muy a menudo, los coeficientes de las ecuaciones son reales o números complejos y las soluciones se buscan en el mismo conjunto de números, pero la teoría y los algoritmos se aplican para los coeficientes y soluciones en cualquier campo. Para soluciones en una dominio integral como el anillo de los números enteros , o en otras estructuras algebraicas , se han desarrollado otras teorías. Véase, por ejemplo, programación lineal entera para soluciones enteras, Base de Gröbner para polinómicas coeficientes e incógnitas, o también geometría tropical para álgebra lineal en una estructura más exótico.
Ejemplo Primaria
El tipo más simple de sistema lineal implica dos ecuaciones y dos variables:
Un método para la resolución de un sistema de este tipo es como sigue. En primer lugar, resolver la ecuación superior para 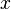 en términos de
en términos de 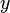 :
:
Ahora sustituye esta expresión para x en la ecuación abajo:
Esto se traduce en una única ecuación que implica solamente la variable 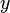 . Solving da
. Solving da 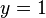 Y Sustituyendo esto en la ecuación para
Y Sustituyendo esto en la ecuación para 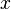 rendimientos
rendimientos 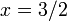 . Este método se generaliza a los sistemas con variables adicionales (ver "de eliminación de variables" a continuación, o el artículo en el álgebra elemental .)
. Este método se generaliza a los sistemas con variables adicionales (ver "de eliminación de variables" a continuación, o el artículo en el álgebra elemental .)
Forma general
Un sistema general de las ecuaciones m lineales con n incógnitas se puede escribir como
Aquí 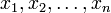 son las incógnitas,
son las incógnitas, 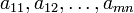 son los coeficientes del sistema, y
son los coeficientes del sistema, y 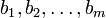 son los términos constantes.
son los términos constantes.
A menudo, los coeficientes y las incógnitas son reales o números complejos , pero enteros y números racionales también se observan, como son polinomios y elementos de un resumen estructura algebraica .
Ecuación vectorial
Un punto de vista muy útil es que cada desconocido es un peso para una vector columna en una combinación lineal.
Esto permite que todo el lenguaje y la teoría de espacios vectoriales (o más generalmente, módulos) para ser llevados a soportar. Por ejemplo, la colección de todas las posibles combinaciones lineales de los vectores en el lado de la izquierda se llama su palmo, y las ecuaciones tienen una solución justa cuando el vector de la mano derecha se encuentra dentro de ese lapso. Si cada vector dentro de ese lapso tiene exactamente una expresión como una combinación lineal de los vectores de la mano izquierda dadas, entonces cualquier solución es única. En cualquier caso, el lapso tiene una base de vectores linealmente independientes que garantizan exactamente una expresión; y el número de vectores en esa base (su dimensión) no puede ser mayor que m o n, pero puede ser más pequeño. Esto es importante porque si tenemos m vectores independientes una solución está garantizada independientemente del lado derecho, y por lo demás no está garantizada.
Ecuación matricial
La ecuación vectorial es equivalente a una matriz ecuación de la forma
donde A es una matriz m × n, x es una vector columna con n entradas, y B es un vector columna con m entradas.
El número de vectores en una base para el lapso ahora se expresa como la rango de la matriz.
Conjunto de soluciones
Una solución de un sistema lineal es una asignación de valores a las variables x 1, x 2, ..., x n de tal manera que cada una de las ecuaciones es satisfecho. El conjunto de todas las soluciones posibles se llama el conjunto solución.
Un sistema lineal puede comportarse de una cualquiera de las tres formas posibles:
- El sistema tiene un número infinito de soluciones.
- El sistema tiene una única solución única.
- El sistema no tiene solución.
Interpretación geométrica
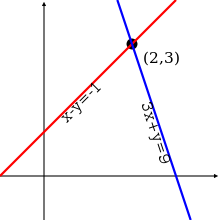
Para un sistema que implica dos variables (x e y), cada ecuación lineal determina una línea en la xy - plano . Debido a que una solución de un sistema lineal debe satisfacer todas las ecuaciones, el conjunto solución es la intersección de estas líneas, y es por lo tanto, ya sea una línea, un único punto, o de la conjunto vacío.
Por tres variables, cada ecuación lineal determina un plano en el espacio tridimensional, y el conjunto solución es la intersección de estos planos. Así, el conjunto solución puede ser un avión, una línea, un solo punto, o el conjunto vacío.
Para n variables, cada una ecuación lineal determina una hiperplano en n espacio dimensional. El conjunto solución es la intersección de estos hiperplanos, que puede ser una plana de cualquier dimensión.
Comportamiento general

En general, el comportamiento de un sistema lineal se determina por la relación entre el número de ecuaciones y el número de incógnitas:
- Por lo general, un sistema con menos ecuaciones que incógnitas tiene infinitas soluciones o soluciones escasas ocasiones únicas ( detección de comprimido). Tal sistema también se conoce como una sistema indeterminado.
- Por lo general, un sistema con el mismo número de ecuaciones e incógnitas tiene una sola solución única.
- Por lo general, un sistema con más ecuaciones que incógnitas no tiene solución. Tal sistema también se conoce como una sistema sobredeterminado.
En el primer caso, la dimensión del conjunto solución es generalmente igual a n - m, donde n es el número de variables y m es el número de ecuaciones.
Las siguientes imágenes ilustran esta tricotomía en el caso de dos variables:

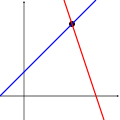
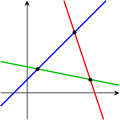
Una ecuación Dos ecuaciones Tres ecuaciones
El primer sistema tiene infinitas soluciones, es decir, todos los puntos de la línea azul. El segundo sistema tiene una única solución única, es decir, la intersección de las dos líneas. El tercer sistema no tiene soluciones, ya que las tres líneas comparten ningún punto común.
Tenga en cuenta que las imágenes de arriba muestran sólo el caso más común. Es posible para un sistema de dos ecuaciones y dos incógnitas no tener solución (si las dos líneas son paralelas), o para un sistema de tres ecuaciones y dos incógnitas para ser resolubles (si las tres líneas se cruzan en un solo punto). En general, un sistema de ecuaciones lineales puede comportarse de manera diferente de lo esperado si las ecuaciones son linealmente dependientes, o si dos o más de las ecuaciones son inconsistentes .
Propiedades
Independencia
Las ecuaciones de un sistema lineal son independientes si ninguna de las ecuaciones se puede derivar algebraicamente de los demás. Cuando las ecuaciones son independientes, cada ecuación contiene nueva información acerca de las variables, y la eliminación de cualquiera de las ecuaciones aumenta el tamaño del conjunto solución. Para ecuaciones lineales, independencia lógica es la misma que independencia lineal.
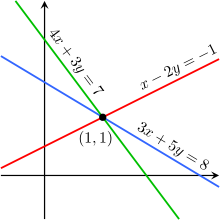
Por ejemplo, las ecuaciones
no son independientes - son la misma ecuación cuando se escala por un factor de dos, y ellos producir gráficos idénticos. Este es un ejemplo de la equivalencia en un sistema de ecuaciones lineales.
Para un ejemplo más complicado, las ecuaciones
no son independientes, porque la tercera ecuación es la suma de los otros dos. De hecho, cualquiera de estas ecuaciones se pueden derivar de los otros dos, y cualquiera de las ecuaciones se puede eliminar sin afectar el conjunto solución. Las gráficas de estas ecuaciones son tres líneas que se cruzan en un solo punto.
Consistencia

Un sistema lineal es consistente si se tiene una solución, e inconsistente lo contrario. Cuando el sistema es inconsistente, es posible derivar una contradicción de las ecuaciones, que siempre se puede reescribir como la declaración 0 = 1.
Por ejemplo, las ecuaciones
son incompatibles. De hecho, restando la primera ecuación de la segunda y multiplicando ambos lados de el resultado por 1/6, se obtiene 0 = 1. Las gráficas de estas ecuaciones en el plano xy xy son un par de lineas paralelas.
Es posible que los tres ecuaciones lineales son incompatibles, a pesar de que cualesquiera dos de ellos son consistentes entre sí. Por ejemplo, las ecuaciones
son incompatibles. Sumando las dos primeras ecuaciones juntos da 3 x 2 + y = 2, que puede ser restado de la tercera ecuación para producir 0 = 1. Tenga en cuenta que dos de estas ecuaciones tienen una solución común. El mismo fenómeno puede ocurrir por cualquier número de ecuaciones.
En general, las inconsistencias se producen si los lados izquierdos de las ecuaciones en un sistema son linealmente dependientes, y los términos constantes no satisfacen la relación de dependencia. Un sistema de ecuaciones cuyos lados izquierdo son linealmente independientes es siempre coherente.
Dicho de otro modo, de acuerdo con la Teorema de Rouché-Capelli, cualquier sistema de ecuaciones (sobredeterminado o de otra manera) es incompatible si el rango de la matriz aumentada es mayor que el rango de la matriz de coeficientes. Si, por otro lado, las filas de estas dos matrices son iguales, el sistema debe tener al menos una solución. La solución es único si y sólo si el rango es igual al número de variables. De lo contrario, la solución general tiene parámetros libres k donde k es la diferencia entre el número de variables y el rango; por lo tanto, en tal caso, hay una infinidad de soluciones.
Equivalencia
Dos sistemas lineales utilizando el mismo conjunto de variables son equivalentes si cada una de las ecuaciones en el segundo sistema se pueden derivar algebraicamente a partir de las ecuaciones en el primer sistema, y viceversa. Dos sistemas son equivalentes si bien ambos son inconsistentes o cada ecuación de cualquiera de ellos es una combinación lineal de las ecuaciones de la otra. De ello se desprende que dos sistemas lineales son equivalentes si y sólo si tienen el mismo conjunto solución.
La solución de un sistema lineal
Hay varios algoritmos para resolver un sistema de ecuaciones lineales.
Al describir la solución
Cuando el conjunto solución es finito, que se reduce a un solo elemento. En este caso, la única solución es descrito por una secuencia de ecuaciones cuya mano izquierda lados son los nombres de las incógnitas y los lados derechos son los valores correspondientes, por ejemplo 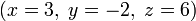 . Cuando una orden de las incógnitas se ha fijado, por ejemplo, el orden alfabético la solución puede ser descrito como un vector de valores, como
. Cuando una orden de las incógnitas se ha fijado, por ejemplo, el orden alfabético la solución puede ser descrito como un vector de valores, como 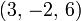 para el ejemplo anterior.
para el ejemplo anterior.
Puede ser difícil para describir un conjunto con infinitas soluciones. Típicamente, algunas de las variables se designan como libre (o independiente, o como parámetros), lo que significa que se les permite tomar cualquier valor, mientras que las restantes variables son dependientes de los valores de las variables libres.
Por ejemplo, considere el siguiente sistema:
El conjunto solución a este sistema puede ser descrito por las siguientes ecuaciones:
Aquí z es la variable libre, mientras que x e y son dependientes de z. Cualquier punto en el conjunto solución puede obtenerse por elegir primero un valor para z, y luego calcular los valores correspondientes para x e y.
Cada variable libre da el espacio solución de un solo grado de libertad, el número de los cuales es igual a la dimensión del conjunto de soluciones. Por ejemplo, el conjunto solución de la ecuación anterior es una línea, desde un punto en el conjunto de soluciones puede ser elegido especificando el valor del parámetro z. Una solución infinita de orden superior puede describir un avión, o un conjunto de dimensiones superiores.
Diferentes opciones para las variables libres pueden dar lugar a diferentes descripciones del mismo conjunto solución. Por ejemplo, la solución a las ecuaciones anteriores, alternativamente, puede ser descrito como sigue:
Aquí x es la variable libre, e Y y Z son dependientes.
Eliminación de variables
El método más simple para resolver un sistema de ecuaciones lineales es eliminar repetidamente variables. Este método puede ser descrito como sigue:
- En la primera ecuación, para resolver una de las variables en términos de los otros.
- Conecte esta expresión en las ecuaciones restantes. Esto produce un sistema de ecuaciones con uno menos ecuación y una incógnita menos.
- Continúe hasta que haya reducido el sistema a una sola ecuación lineal.
- Resolver esta ecuación y, a continuación, una copia de sustituto hasta que se encuentra toda la solución.
Por ejemplo, considere el siguiente sistema:
La solución de la primera ecuación para x da x = 5 + 2 z - 3 y, y enchufar esto en las segunda y tercera rendimientos de ecuaciones
. La solución de la primera de estas ecuaciones para los rendimientos Y Y = 2 + 3 z, y enchufar esto en los rendimientos segunda ecuación z = 2 Ahora tenemos:
Sustituyendo z = 2 en la segunda ecuación da y = 8, y sustituyendo z = 2 e y = 8 en los rendimientos primera ecuación x = -15. Por lo tanto, el conjunto solución es el único punto (x, y, z) = (-15, 8, 2).
Reducción Fila
En la reducción de fila, el sistema lineal se representa como un matriz aumentada:
Esta matriz se modifica a continuación, utilizando operaciones elementales de renglón hasta que alcanza forma escalonada reducida. Hay tres tipos de operaciones elementales de fila:
- Tipo 1: intercambiar las posiciones de dos filas.
- Tipo 2: Multiplicar una fila por un distinto de cero escalar.
- Tipo 3: Añadir a una fila un múltiplo escalar del otro.
Debido a que estas operaciones son reversibles, la matriz aumentada producido siempre representa un sistema lineal que es equivalente a la original.
Hay varios algoritmos específicos para remar-reducir una matriz aumentada, el más simple de los cuales son la eliminación de Gauss y Eliminación de Gauss-Jordan. El siguiente cálculo muestra eliminación de Gauss-Jordan aplicado a la matriz anterior:
La última matriz está en forma escalonada reducida, y representa el sistema x = -15, y = 8, z = 2. Una comparación con el ejemplo en la sección anterior sobre la eliminación algebraica de las variables muestra que estos dos métodos son de hecho lo mismo; la diferencia radica en cómo los cálculos están escritas.
La regla de Cramer
La regla de Cramer es una fórmula explícita para la solución de un sistema de ecuaciones lineales, con cada variable dada por un cociente de dos determinantes . Por ejemplo, la solución del sistema
es dado por
Para cada variable, el denominador es el determinante de la matriz de coeficientes, mientras que el numerador es el determinante de una matriz en la que una columna se ha sustituido por el vector de términos constantes.
Aunque la regla de Cramer es importante teóricamente, tiene poco valor práctico para grandes matrices, ya que el cálculo de grandes determinantes es algo engorroso. (De hecho, los grandes determinantes se calculan más fácilmente mediante la reducción de la fila). Además, la regla de Cramer tiene muy malas propiedades numéricas, por lo que es inadecuado para solucionar sistemas incluso pequeñas fiable, a menos que las operaciones se realizan en la aritmética racional con precisión ilimitada.
Solución de matriz
Si el sistema de ecuación se expresa en la forma de matriz 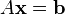 , Todo el conjunto solución también se puede expresar en forma de matriz. Si la matriz A es cuadrada (tiene m filas y n = m columnas) y tiene rango completo (todas las filas m son independientes), entonces el sistema tiene una única solución dada por
, Todo el conjunto solución también se puede expresar en forma de matriz. Si la matriz A es cuadrada (tiene m filas y n = m columnas) y tiene rango completo (todas las filas m son independientes), entonces el sistema tiene una única solución dada por
donde 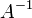 es el inversa de A. Más en general, independientemente de si m = n o no e independientemente del rango de A, todas las soluciones (si existe alguno) se dan utilizando el Moore-Penrose pseudoinversa de A, denotado
es el inversa de A. Más en general, independientemente de si m = n o no e independientemente del rango de A, todas las soluciones (si existe alguno) se dan utilizando el Moore-Penrose pseudoinversa de A, denotado 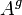 , Como sigue:
, Como sigue:
donde 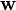 es un vector de parámetros libres que se extiende sobre toda posible n × 1 vectores. Una condición necesaria y suficiente para cualquier solución (s) de existir es que la solución obtenida usando potencial
es un vector de parámetros libres que se extiende sobre toda posible n × 1 vectores. Una condición necesaria y suficiente para cualquier solución (s) de existir es que la solución obtenida usando potencial 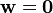 satisfacer
satisfacer 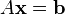 - Eso es eso
- Eso es eso 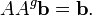 Si esta condición no se cumple, el sistema de ecuaciones es incompatible y no tiene solución. Si la condición se cumple, el sistema es consistente y existe al menos una solución. Por ejemplo, en el caso antes mencionado en la que A es cuadrada y de rango completo,
Si esta condición no se cumple, el sistema de ecuaciones es incompatible y no tiene solución. Si la condición se cumple, el sistema es consistente y existe al menos una solución. Por ejemplo, en el caso antes mencionado en la que A es cuadrada y de rango completo, 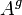 simplemente es igual
simplemente es igual 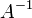 y la ecuación se simplifica a solución general
y la ecuación se simplifica a solución general 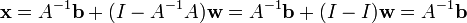 como se dijo anteriormente, en donde
como se dijo anteriormente, en donde 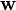 ha caído completamente fuera de la solución, dejando sólo una única solución. En otros casos, sin embargo,
ha caído completamente fuera de la solución, dejando sólo una única solución. En otros casos, sin embargo, 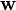 y por lo tanto sigue siendo una infinidad de valores posibles del parámetro vector libre
y por lo tanto sigue siendo una infinidad de valores posibles del parámetro vector libre 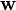 dar una infinidad de soluciones de la ecuación.
dar una infinidad de soluciones de la ecuación.
Otros métodos
Mientras que los sistemas de tres o cuatro ecuaciones se pueden resolver fácilmente a mano, los ordenadores a menudo se utilizan para sistemas más grandes. El algoritmo estándar para resolver un sistema de ecuaciones lineales se basa en la eliminación de Gauss con algunas modificaciones. En primer lugar, es esencial para evitar la división por números pequeños, que pueden dar lugar a resultados inexactos. Esto se puede hacer por la reordenación de las ecuaciones si es necesario, un proceso conocido como pivotante. En segundo lugar, el algoritmo no hace exactamente eliminación de Gauss, pero calcula la Descomposición LU de la matriz A. Esto es principalmente una herramienta de organización, pero es mucho más rápido si uno tiene que resolver varios sistemas con la misma matriz A, pero diferentes vectores b.
Si la matriz A tiene una estructura especial, esto puede ser explotado para obtener algoritmos más rápido o más precisos. Por ejemplo, los sistemas con una simétrico matriz definida positiva se puede resolver el doble de rápido con el Descomposición de Cholesky. Recursión de Levinson es un método rápido para Matrices Toeplitz. Existen métodos especiales también para matrices con muchos elementos cero (los llamados matrices dispersas), que aparecen a menudo en aplicaciones.
Un enfoque completamente diferente se toma a menudo para sistemas muy grandes, que de otra manera tomaría demasiado tiempo o la memoria. La idea es comenzar con una primera aproximación a la solución (que no tiene por qué ser exacta del todo), y para cambiar esta aproximación en varios pasos para acercarla a la verdadera solución. Una vez que la aproximación es suficientemente precisa, esto se toma como la solución para el sistema. Esto conduce a la clase de métodos iterativos.
Sistemas homogéneos
Un sistema de ecuaciones lineales es homogénea si todos los términos constantes son cero:
Un sistema homogéneo es equivalente a una ecuación de la matriz de la forma
donde A es una matriz m × n, x es un vector columna con n entradas, y 0 es la vector cero con m entradas.
Conjunto de soluciones
Cada sistema homogéneo tiene al menos una solución, conocida como la solución de cero (o solución trivial), que se obtiene mediante la asignación de un valor de cero para cada una de las variables. Si el sistema tiene una matriz no singular (det (A) ≠ 0), entonces también es la única solución. Si el sistema tiene una matriz singular, entonces hay un conjunto de soluciones con un número infinito de soluciones. Este conjunto solución tiene las siguientes propiedades adicionales:
- Si u y v son dos vectores que representan soluciones a un sistema homogéneo, entonces el vector suma u + v es también una solución para el sistema.
- Si u es un vector que representa una solución a un sistema homogéneo, y R es cualquier escalar, entonces R u es también una solución para el sistema.
Estas son exactamente las propiedades requeridas para la solución prevista para ser una subespacio lineal de R n. En particular, el conjunto solución a un sistema homogéneo es el mismo que el espacio nulo de la matriz correspondiente A.
Relación con los sistemas no homogéneos
Existe una estrecha relación entre las soluciones de un sistema lineal y las soluciones al sistema homogéneo correspondiente:
Específicamente, si p es cualquier solución específica para el sistema lineal A x = b, entonces todo el conjunto de soluciones puede ser descrito como
Geométricamente, esto dice que el conjunto solución de Ax = b es una traducción del conjunto de soluciones para A x = 0. Específicamente, la piso en el primer sistema se puede obtener mediante la traducción de la subespacio lineal para el sistema homogéneo por el vector p.
Este razonamiento se aplica solamente si el sistema A x = b tiene al menos una solución. Esto ocurre si y sólo si el vector b se encuentra en el imagen de la Una transformación lineal.

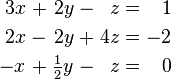
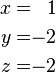
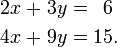
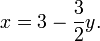
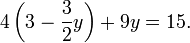
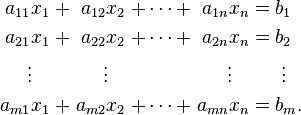
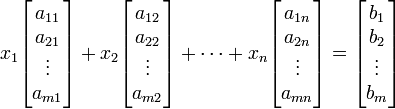
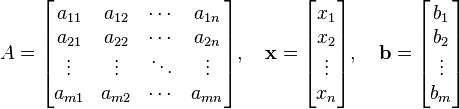
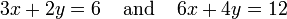
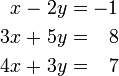
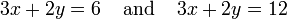
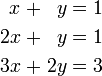
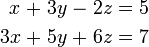
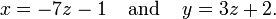
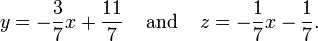
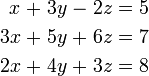
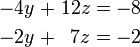
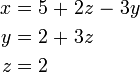
![\ Left [\ begin {array} {rrr | r} 1 y 3 y -2 y 5 \\ 3 & 5 & 6 & 7 \\ 2 y 4 y 3 y 8 \ end {array} \ right] \ text { .}](../../images/1643/164330.png)
![\ Begin {align} \ left [\ begin {array} {rrr | r} 1 y 3 y -2 y 5 \\ 3 & 5 & 6 & 7 \\ 2 y 4 y 3 y 8 \ end {array} \ right] y \ sim \ left [\ begin {array} {rrr | r} 1 y 3 y -2 y 5 \\ 0 & -4 y 12 y -8 \\ 2 y 4 y 3 y 8 \ end {array } \ right] \ sim \ left [\ begin {array} {rrr | r} 1 y 3 y -2 y 5 \\ 0 & -4 y 12 y -8 \\ 0 & -2 y 7 y -2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 y 3 y -2 y 5 \\ 0 & 1 y -3 y 2 \\ 0 & -2 y 7 & - 2 \ end {array} \ right] \\ & \ sim \ left [\ begin {array} {rrr | r} 1 y 3 y -2 y 5 \\ 0 & 1 y -3 y 2 \\ 0 & 0 y 1 y 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 y 3 y -2 y 5 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 0 & 9 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right]. \ end {align}](../../images/1643/164331.png)