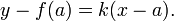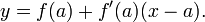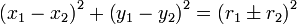Tangente
Antecedentes de las escuelas de Wikipedia
Esta selección se hace para las escuelas por caridad para niños leer más . Apadrinar un niño para hacer una diferencia real.

En la geometría , la línea tangente (o simplemente la tangente) a una curva en un momento dado punto es la línea recta que "sólo toca" la curva en ese punto (en el sentido explicado más precisa a continuación). Al pasar por el punto de tangencia, la línea tangente "va en la misma dirección", como la curva, y en este sentido es la mejor aproximación de línea recta a la curva en ese punto. La misma definición se aplica a las curvas en el espacio y curvas en n-dimensional espacio euclidiano .
De una manera similar, el plano tangente a una superficie en un punto dado es el plano que "sólo toca" la superficie en ese punto. El concepto de la tangente es una de las nociones más fundamentales de la geometría diferencial y se ha generalizado ampliamente - ver Espacio tangente.
La palabra "tangente" viene del latín tangere, que significa "tocar".
Recta tangente a una curva
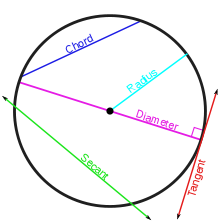
La noción intuitiva de que la tangente "sólo toca" una curva puede ser más explícito al considerar la secuencia de líneas rectas ( líneas secantes) que pasan a través de dos puntos, A y B, que se encuentran en la curva. La tangente en A es el límite de la progresión de las líneas secantes como B se mueve cada vez más cerca de una. La existencia y unicidad de la línea tangente depende de un cierto tipo de suavidad matemática, conocida como "diferenciabilidad". Por ejemplo, si dos arcos circulares se encuentran en un punto afilado (un vértice) entonces no hay tangente definida de forma única en el vértice porque el límite de la progresión de las líneas secantes depende de la dirección en la que "punto B" se acerca al vértice.
En la mayoría de los casos encontrados comúnmente, la tangente a una curva no cruza la curva en el punto de tangencia (aunque puede, cuando continuó, cruce la curva en otros lugares de distancia desde el punto de tangencia). Esto es cierto, por ejemplo, de todas las tangentes a un círculo o una parábola. Sin embargo, en los puntos excepcionales llamada puntos de inflexión, la línea tangente atraviesa la curva en el punto de tangencia. Un ejemplo es el punto (0,0) en la gráfica de la parábola y = x 3 cúbico.
Por el contrario, puede ocurrir que la curva se encuentra completamente a un lado de una línea recta que pasa a través de un punto sobre el mismo, y sin embargo, esta línea recta no es una línea tangente. Este es el caso, por ejemplo, por una línea que pasa por el vértice de un triángulo y el triángulo no interecting - donde la línea tangente no existe por las razones explicadas anteriormente. En geometría convexa, dichas líneas se llaman líneas de apoyo.
Enfoque analítico
La idea geométrica de la línea tangente como el límite de las líneas secantes sirve de motivación para los métodos analíticos que se utilizan para encontrar líneas tangentes explícitamente. La cuestión de encontrar la recta tangente a una gráfica, o el problema de la línea tangente, fue una de las cuestiones centrales que conducen al desarrollo de cálculos en el siglo 17. En el segundo libro de su geometría René Descartes dijo sobre el problema de la construcción de la tangente a una curva, "Y me atrevo a decir que esto no es sólo el problema más útil y más general en la geometría, que yo sepa, pero incluso eso siempre he deseado conocer."
Descripción intuitiva
Supongamos que una curva se da como la gráfica de una función , y = f (x). Para encontrar la línea tangente en el punto P = (a, f (a)), considere otro punto cercano q = (a + h, f (a + h)) en la curva. La pendiente de la línea secante que pasa por p y q es igual a la cociente de diferencias
Como el punto q se acerca p, que corresponde a lo que h más y más pequeña, el cociente de la diferencia debe acercarse a un cierto valor k limitante, que es la pendiente de la línea tangente en el punto p. Si se conoce k, la ecuación de la recta tangente se puede encontrar en la forma punto-pendiente:
Una descripción más rigurosa
Para hacer que el razonamiento anterior riguroso, hay que explicar qué se entiende por el cociente de diferencias acercarse a un determinado valor límite k. La formulación matemática precisa fue dada por Cauchy en el siglo 19 y se basa en la noción de límite . Supongamos que la gráfica no tiene un descanso o un borde afilado en py no es ni plomo ni demasiado cerca wiggly p. Entonces hay un valor único de k tal que como h se aproxima a 0, el cociente de la diferencia se acerca más y más cerca a k, y la distancia entre ellos se convierte en insignificante en comparación con el tamaño de h, si h es lo suficientemente pequeño. Esto conduce a la definición de la pendiente de la recta tangente a la gráfica como el límite de los cocientes de diferencias de la función f. Este límite es el derivado de la función f en x = a, denotado f '(a). El uso de derivados, la ecuación de la recta tangente puede enunciarse como sigue:
Cálculo proporciona reglas para el cálculo de las derivadas de las funciones que se dan por fórmulas, como la función de potencia, funciones trigonométricas , función exponencial , logaritmo , y sus diversas combinaciones. Así, las ecuaciones de las tangentes a gráficos de todas estas funciones, así como muchos otros, se pueden encontrar por los métodos de cálculo.
Cuando el método falla
Cálculo también demuestra que hay funciones y puntos en sus gráficas para el que no existe el límite de la determinación de la pendiente de la línea tangente. Para estos puntos de la función f no es diferenciable. Hay dos posibles razones para el método de búsqueda de las tangentes en base a los límites y derivados a fallar: o bien existe la tangente geométrica, pero es una línea vertical, que no se puede dar en forma punto-pendiente, ya que no tiene un pendiente, o el gráfico está demasiado mal comportaron a admitir la tangente geométrica.
El gráfico y = x 1/3 ilustra la primera posibilidad: aquí el cociente de diferencias en a = 0 es igual a 3.1 h / h = h - 2/3, que se hace muy grande cuando h tiende a 0. La recta tangente a esta curva en el origen es vertical.
El gráfico y = | x | de la valor absoluto función consiste en dos líneas rectas con diferentes pendientes se unió en el origen. Como punto q se acerca al origen de la derecha, la línea secante siempre tiene pendiente 1. Como punto q se acerca al origen de la izquierda, la línea secante siempre tiene pendiente -1. Por lo tanto, no hay tangente única para el gráfico en el origen (aunque en cierto sentido, hay dos medio-tangentes, correspondientes a dos posibles direcciones de aproximación al origen).

Círculos tangentes
Dos círculos , con radios de r i y centros en (x i, y i), para i = 1, 2 se dice que son tangentes entre sí, si
Las superficies y los colectores de dimensiones superiores
El plano tangente a una superficie en un punto p dado se define de una manera análoga a la línea tangente en el caso de curvas. Es la mejor aproximación de la superficie por un plano en p, y se puede obtener como la posición de limitación de los planos que pasan a través de 3 puntos distintos en la superficie cerca de p ya que estos puntos convergen para p. Más en general, hay una k-dimensional espacio tangente en cada punto de un -dimensional k colector en el n-dimensional espacio euclidiano .