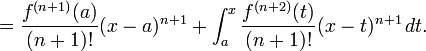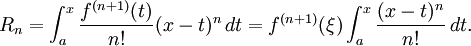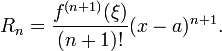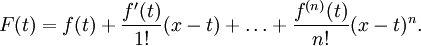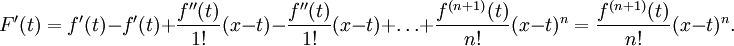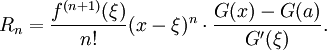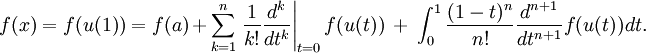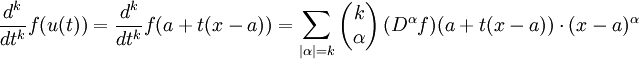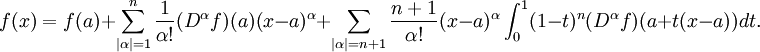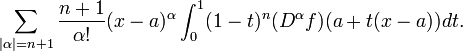El teorema de Taylor
Sabías ...
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.
En el cálculo , el teorema de Taylor da una secuencia de aproximaciones de un diferenciable función cerca de un punto dado por polinomios (los polinomios de Taylor de esa función) cuyos coeficientes dependen sólo de las derivadas de la función en ese punto. El teorema también las estimaciones precisas sobre el tamaño del error en la aproximación. El teorema recibe su nombre del matemático Brook Taylor, quien afirmó que en 1712, aunque el resultado fue descubierta 41 años antes en 1671 por James Gregory.
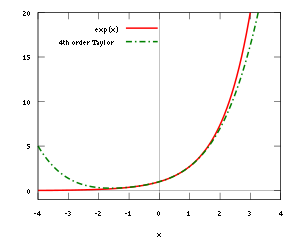
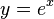 (Línea continua roja) y el correspondiente polinomio de Taylor de grado cuatro en torno al origen (línea verde discontinua).
(Línea continua roja) y el correspondiente polinomio de Taylor de grado cuatro en torno al origen (línea verde discontinua). El teorema de Taylor en una variable
Un ejemplo simple del teorema de Taylor es la aproximación de la función exponencial 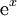 cerca de x = 0:
cerca de x = 0:
La indicación precisa del teorema es como sigue: Si n ≥ 0 es un número entero y f es una función que es n veces continuamente diferenciable en el intervalo cerrado [a, x] y n + 1 veces diferenciable en el intervalo abierto (a, x), entonces tenemos
Aquí, n! denota el factorial de n, R y n (x) es un término resto, que denota la diferencia entre el polinomio de Taylor de grado n y la función original. El término resto R n (x) depende de x es pequeño y si x es lo suficientemente cerca de a. Varias expresiones están disponibles para él.
El Lagrange forma del término resto afirma que existe un número ξ entre a y x tal que
Esto expone el teorema de Taylor como una generalización de la teorema del valor medio. De hecho, el teorema de valor medio se utiliza para probar el teorema de Taylor con el término resto Lagrange.
La Forma Cauchy del término resto afirma que existe un número ξ entre A y x tal que
Más generalmente, si G (t) es una función continua en [a, x], que es diferenciable con derivado no desapareciendo en (a, x), entonces existe un número ξ entre a y x tal que
Esto expone el teorema de Taylor como una generalización de la Cauchy teorema del valor medio.
El integrante forma del término resto es
proporcionado, como es a menudo el caso, f (n) es absolutamente continua en [a, x]. Esto demuestra el teorema de ser una generalización del teorema fundamental del cálculo .
Para algunas funciones f (x), se puede demostrar que el plazo que resta R n tiende a cero cuando n tiende a ∞; esas funciones se pueden expresar como una serie de Taylor en una entorno del punto a y se llaman analítico.
El teorema de Taylor (con la formulación integral del término resto) también es válido si la función f tiene complejos valores o vector valores. Además, hay una versión del teorema de Taylor para funciones de varias variables.
Para las funciones complejas analítica en una región que contiene un círculo C que rodea a una y su interior, tenemos una expresión integral de contorno para el resto
dentro válida de C.
Las estimaciones de el resto
Otra versión común del teorema de Taylor mantiene en un intervalo (a - r, a + r) donde se supone que la variable X para tomar sus valores. Esta formulación del teorema tiene la ventaja de que a menudo es posible controlar de forma explícita el tamaño de los términos restantes, y por lo tanto llegar a una aproximación de una función válida en todo un intervalo con límites precisos sobre la calidad de la aproximación.
Una versión exacta del teorema de Taylor en este formulario es el siguiente. Supongamos que f es una función que es n veces continuamente diferenciable en el intervalo cerrado [a - r, a + r] y n + 1 veces derivable en el intervalo abierto (a - r, a + r). Si existe una constante real positiva M n tal que | f (n + 1) (x) | ≤ M n para todo x ∈ (a - r, a + r), entonces
donde el resto función R n satisface la desigualdad (conocido como estimación de Cauchy):
para todo x ∈ (a - r, a + r). Esto se llama una estimación uniforme del error en el polinomio de Taylor centrada en una, porque lleva a cabo de manera uniforme para todos los x en el intervalo.
Si, además, f es infinitamente diferenciable en [a - r, a + r] y
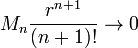 como
como 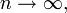
entonces f es analítica en (a - r, a + r). En otras palabras, una función analítica es la límite uniforme de su polinomios de Taylor en un intervalo. Esto hace precisa la idea de que las funciones analíticas son aquellos que son igual a su serie de Taylor.
El teorema de Taylor para varias variables
El teorema de Taylor se puede generalizar a varias variables como sigue. Sea B un pelota en R N centrada en un punto a, y f una función real definida en el cierre 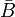 tener n 1 derivadas parciales continuas en cada punto. El teorema de Taylor afirma que para cualquier
tener n 1 derivadas parciales continuas en cada punto. El teorema de Taylor afirma que para cualquier 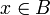 ,
,
donde la suma se extiende sobre múltiples índices α (esta fórmula utiliza el notación multi-índice).
Los términos restantes satisfacen la desigualdad
para todos α con | α | = n +1. Como fue el caso con una variable, los términos restantes se pueden describir de forma explícita. Véase la prueba para más detalles.
Prueba: el teorema de Taylor en una variable
Versión Integral
En primer lugar, demostrar el teorema de Taylor con el término restante integral.
El teorema fundamental del cálculo establece que
que puede ser reorganizado para:
Ahora podemos ver que una aplicación de Integración por partes se obtiene:
(La primera ecuación se llega a al permitir 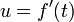 y
y 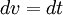 ; la segunda ecuación por señalar que
; la segunda ecuación por señalar que 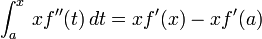 ; el tercero sólo factores de algunos términos comunes.)
; el tercero sólo factores de algunos términos comunes.)
Otra aplicación rendimientos:
Repitiendo este proceso, podemos derivar el teorema de Taylor para los valores más altos de n.
Esto se puede formalizar mediante la aplicación de la técnica de inducción. Por lo tanto, supongamos que el teorema de Taylor se mantiene para una n en particular, es decir, supongamos que
Podemos reescribir la integral usando integración por partes. Una primitiva de (x - t) n como una función de t está dada por - (x - t) n 1 / (n + 1), por lo
Sustituyendo esto en (*) demuestra el teorema de Taylor para n + 1, y por lo tanto para todos los enteros no negativos n.
El término resto en la forma Lagrange se puede derivar por el significar teorema del valor de la siguiente manera:
La última integral puede ser resuelto inmediatamente, lo que conduce a
Teorema del valor medio
Una prueba alternativa, que tiene bajo supuestos técnicos más leves de la función f, se puede suministrar con el Cauchy teorema del valor medio. Sea G un función real continua en [a, x] y derivable con derivada no nula en (a, x). Dejar
Por teorema del valor medio de Cauchy,
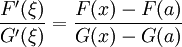 (1)
(1)
para algunos ∈ ξ (a, x). Tenga en cuenta que el numerador F (x) - F (a) = R n es el resto del polinomio de Taylor para f (x). Por otro lado, el cálculo de F '(t),
Poniendo estos dos hechos juntos y reordenando los términos de (1) los rendimientos
que iba a ser mostrado.
Tenga en cuenta que la forma de Lagrange el resto viene de tomar G (t) = (t - a) n 1, y la forma dada de Cauchy el resto viene de tomar G (t) = (t - a).
Prueba: varias variables
Sea x = (x 1, ..., x N) se encuentran en la bola B con un centro. Parametrizar el segmento de línea entre A y X por u (t) = a + t (xa). Aplicamos la versión de una variable del teorema de Taylor para la función f (u (t)):
Por el regla de la cadena para varias variables,
donde  es el coeficiente multinomial para el α multi-índice. Desde
es el coeficiente multinomial para el α multi-índice. Desde 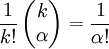 , Obtenemos
, Obtenemos
El término resto está dada por
Los términos de esta suma son formas explícitas para la R α en la declaración del teorema. Estos se ven fácilmente para satisfacer la estimación requerida.

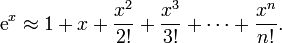
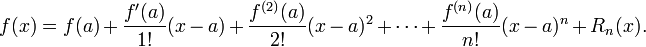
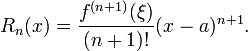
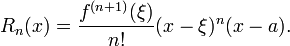
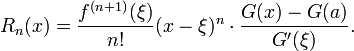
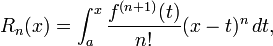
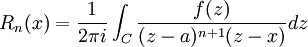
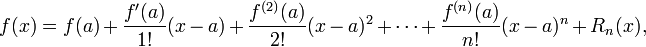
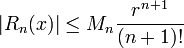
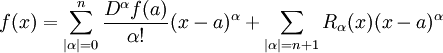
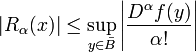
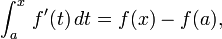
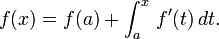
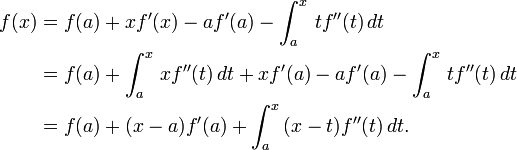
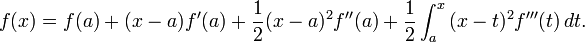
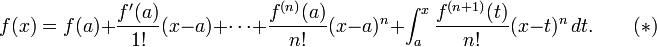
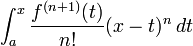
![{} = - \ Left [\ frac {f ^ {(n + 1)} (t)} {(n + 1) n!} (X - t) ^ {n + 1} \ right] _a ^ x + \ int_a ^ x \ frac {f ^ {(n + 2)} (t)} {(n + 1) n!} (x - t) ^ {n + 1} \, dt](../../images/127/12701.png)