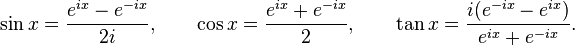Trigonometría
Acerca de este escuelas selección Wikipedia
Los artículos de esta selección escuelas se han organizado por tema currículo gracias a voluntarios SOS. SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?

| Trigonometría |
|---|
| Historia Uso Funciones Generalizada Funciones inversas Otras lecturas |
| Referencia |
| Identidades Constantes Exactas Tablas trigonométricas |
| Las leyes y teoremas |
| Ley de los senos Ley de los cosenos Ley de las tangentes Ley de cotangentes Teorema de pitágoras |
| Cálculo |
| Sustitución trigonométrica Integrales de funciones Derivadas de funciones Integrales de funciones inversas |
Trigonometría (del griego Trigonon "triángulo" + metron "medida") es una rama de las matemáticas que estudia los triángulos y las relaciones entre las longitudes de sus lados y los ángulos entre los lados. Trigonometría define las funciones trigonométricas , que describen esas relaciones y tienen aplicabilidad a fenómenos cíclicos, como las olas. El campo se desarrolló durante el siglo III aC como una rama de la geometría se utiliza ampliamente para estudios astronómicos. También es la base del arte práctico de agrimensura.
Fundamentos Trigonometría muchas veces son impartidos en la escuela , ya sea como un curso separado o como parte de una curso de precálculo. Las funciones trigonométricas son omnipresentes en partes de matemáticas puras y matemáticas aplicadas como Análisis de Fourier y la ecuación de onda, que son a su vez esenciales para muchas ramas de la ciencia y la tecnología. Estudios de trigonometría esférica triángulos en esferas , superficies de constante positiva curvatura, en geometría elíptica. Es fundamental para la astronomía y navegación. Trigonometría en superficies de curvatura negativa es parte de Geometría hiperbólica.
Historia

Sumerias astrónomos introdujeron medida del ángulo, utilizando una división de los círculos en 360 grados. Ellos y sus sucesores los babilonios estudiaron las relaciones de los lados de los triángulos semejantes y descubrieron algunas propiedades de estas proporciones, pero no convertirlo en un método sistemático para encontrar lados y ángulos de triángulos. La antigua nubios utiliza un método similar. Los antiguos griegos transformaron trigonometría en una ciencia ordenado.
Clásico Matemáticos griegos (tales como Euclides y Arquímedes ) estudiaron las propiedades de acordes y ángulos inscritos en círculos, y demostraron teoremas que son equivalentes a las fórmulas trigonométricas modernas, a pesar de que ellos presentan geométricamente en lugar de forma algebraica. Claudio Ptolomeo ampliarán Acordes de Hiparco en un círculo en su Almagesto. El moderno función seno se definió por primera vez en la Surya Siddhanta, y sus propiedades fueron documentados aún más por el siglo quinto matemático indio y astrónomo Aryabhata. Estas obras griegas e indias fueron traducidos y expandido en matemáticos islámicos medievales. Por el siglo 10, los matemáticos islámicos estaban usando las seis funciones trigonométricas, había tabulada sus valores, y fueron aplicarlos a problemas en geometría esférica. Casi al mismo tiempo, Matemáticos chinos desarrollaron trigonometría independiente, aunque no fue un importante campo de estudio para ellos. Conocimiento de las funciones y métodos trigonométricos llegó a Europa a través de Traducciones latinas de las obras de Los astrónomos persas y árabes como Al Battani y Nasir al-Din al-Tusi. Uno de los primeros trabajos sobre trigonometría por un matemático europea es DE Triangulis por el siglo 15 alemán matemático Regiomontano. Trigonometría fue todavía tan poco conocido en Europa del siglo 16 que Nicolás Copérnico dedicó dos capítulos de De revolutionibus orbium coelestium a explicar sus conceptos básicos.
Impulsada por las demandas de la navegación y la creciente necesidad de mapas precisos de grandes áreas, la trigonometría se convirtieron en una gran rama de las matemáticas. Bartolomé Pitiscus fue el primero en usar la palabra, publicando su Trigonometria en 1595. Gemma Frisius describe por primera vez el método de triangulación todavía se utiliza hoy en topografía. Fue Leonhard Euler que incorpore plenamente los números complejos en trigonometría. Las obras de James Gregory en el siglo 17 y Colin Maclaurin en el siglo 18 fueron influyentes en el desarrollo de las series trigonométricas. También en el siglo 18, Brook Taylor definió el general de la serie de Taylor .
Visión de conjunto

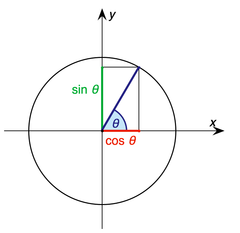
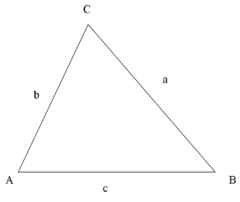
Si un ángulo de un triángulo es 90 grados y uno de los otros ángulos se sabe, la tercera con ello se fija, ya que los tres ángulos de cualquier triángulo suman 180 grados. Por tanto, los dos ángulos agudos suman a 90 grados: son ángulos complementarios. La forma de un triángulo se determina por completo, a excepción de similitud, por los ángulos. Una vez que se conocen los ángulos, el proporciones de los lados se determinan, independientemente del tamaño global del triángulo. Si se conoce la longitud de uno de los lados, los otros dos se determinan. Estas relaciones están dadas por las siguientes funciones trigonométricas del ángulo Un conocido, donde a, b y c a las longitudes de los lados de la figura adjunta:
- Función seno (SIN), definido como la relación entre el lado opuesto al ángulo a la hipotenusa.
- Coseno función de (cos), definida como la relación de la cateto adyacente a la hipotenusa.
- Tangente función (TAN), definido como la relación de la pierna opuesta a la pata adyacente.
La hipotenusa es el lado opuesto al ángulo de 90 grados en un triángulo rectángulo; es el lado más largo del triángulo, y uno de los dos lados adyacentes a ángulo A. El cateto adyacente es el otro lado que es adyacente al ángulo A. El lado opuesto es el lado que es opuesto al ángulo A. Los términos perpendiculares y la base se utilizan a veces para los lados opuestos y adyacentes respectivamente. Muchas personas de habla inglesa les resulta fácil recordar lo lados del triángulo rectángulo es igual al seno, coseno, tangente o, memorizando la palabra SOH-CAH-TOA (ver más adelante bajo mnemotécnicos ).
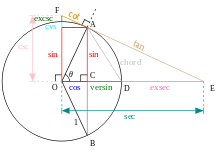
La recíprocos de estas funciones se nombran la cosecante (csc o cosec), secante (sec), y cotangente (cuna), respectivamente:
La funciones inversas se denominan el arcoseno, arcocoseno, y arcotangente, respectivamente. Hay relaciones aritméticas entre estas funciones, que se conocen como identidades trigonométricas. El coseno, cotangente y cosecante se llaman así porque son respectivamente el seno, tangente y secante del ángulo complementario abreviado a "cooperación".
Con estas funciones se puede responder a prácticamente todas las preguntas acerca de triángulos arbitrarios mediante el uso de la ley de los senos y la ley de los cosenos. Estas leyes se pueden utilizar para calcular los ángulos restantes y los lados de cualquier triángulo tan pronto como las dos caras y su ángulo incluido o dos ángulos y un lado o tres lados son conocidos. Estas leyes son útiles en todas las ramas de la geometría, puesto que cada polígono se puede describir como una combinación finito de triángulos.
La ampliación de las definiciones
Las definiciones anteriores se aplican a los ángulos entre 0 y 90 grados (0 y π / 2 radianes ) solamente. Usando el círculo unidad, se puede extender a todos los argumentos positivos y negativos (ver función trigonométrica ). Las funciones trigonométricas son periódica, con un período de 360 grados o 2π radianes. Eso significa que sus valores se repiten en esos intervalos. Las funciones tangente y cotangente también tienen un período más corto, de 180 grados o π radianes.
Las funciones trigonométricas se pueden definir de otras maneras además de las definiciones geométricas anteriormente, usando herramientas de cálculo y serie infinita. Con estas definiciones de las funciones trigonométricas se pueden definir para los números complejos . La función exponencial compleja es particularmente útil.
Ver Euler y Fórmulas de De Moivre.

Proceso gráfica de y = sin (x) usando un círculo unidad.
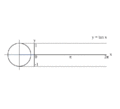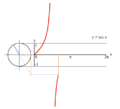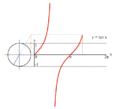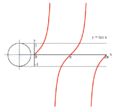
Proceso gráfica de y = tan (x) usando un círculo unidad.
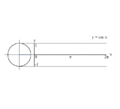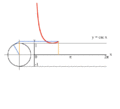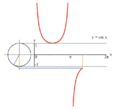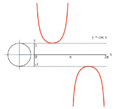
Proceso gráfica de y = csc (x) usando un círculo unidad.
Nemotécnica
Un uso común de mnemotecnia es recordar hechos y relaciones en trigonometría. Por ejemplo, el seno, coseno, tangente y ratios en un triángulo rectángulo puede ser recordado por lo que representa como una cadena de letras. Por ejemplo, una regla mnemotécnica para los angloparlantes es SOH-CAH-TOA:
- S ine = O pposite ÷ H ypotenuse
- C osine = A H ypotenuse ÷ djacent
- Tangente = O pposite ÷ Un djacent
Una forma de recordar las letras es pronunciarlas fonéticamente (es decir, SOH-CAH-TOA, que se pronuncia 'tow tan kə-' -uh '). Otro método consiste en ampliar las letras en una frase, como "S ome O ld H ippy C nada O tro H ippy T Rippin 'O n A cid".
Cálculo de funciones trigonométricas
Funciones trigonométricas fueron algunos de los primeros usos de tablas matemáticas. Estas tablas se incorporaron en los libros de texto de matemáticas y los estudiantes se les enseña a buscar valores y la forma de interpolar entre los valores indicados para conseguir una mayor precisión. Las reglas de cálculo tenían escalas especiales para las funciones trigonométricas.
Hoy calculadoras científicas tienen botones para el cálculo de las principales funciones trigonométricas (sin, cos, tan, ya veces cis y sus inversas. La mayoría permiten una elección de los métodos de medición de ángulos: grados, radianes y, a veces, grad. La mayoría de las computadoras lenguajes de programación proporcionan bibliotecas de funciones que incluyen las funciones trigonométricas. La hardware unidad de punto incorporado en los chips de microprocesadores utilizados en la mayoría de los ordenadores personales tienen instrucciones incorporadas para el cálculo de las funciones trigonométricas flotante.
Aplicaciones de la trigonometría

Hay una enorme cantidad de usos de la trigonometría y funciones trigonométricas. Por ejemplo, la técnica de triangulación se utiliza en astronomía para medir la distancia a las estrellas cercanas, en la geografía para medir distancias entre puntos de referencia, y en sistemas de navegación por satélite. Las funciones seno y coseno son fundamentales para la teoría de la funciones periódicas tales como los que describen de sonido y de luz olas.
Los campos que utilizan funciones trigonométricas o trigonométricas incluyen astronomía (especialmente para localizar las posiciones aparentes de los objetos celestes, en el que la trigonometría esférica es esencial) y por lo tanto navegación (en los océanos, en los aviones, y en el espacio), teoría de la música, acústica, la óptica , el análisis de los mercados financieros, la electrónica , teoría de la probabilidad , estadísticas , biología , imagenes medicas ( TAC y ultrasonido), farmacia, química , teoría de números (y por tanto la criptología ), sismología, meteorología , oceanografía , muchas ciencias físicas , de la tierra topografía y geodesia, arquitectura , fonética, economía , ingeniería eléctrica , ingeniería mecánica , ingeniería civil , gráficos de computadora, cartografía, cristalografía y el desarrollo del juego.
Identidades estándar
Las identidades son aquellas ecuaciones que son válidas para cualquier valor.
Fórmulas de transformación de ángulo
Fórmulas comunes
Ciertas ecuaciones con funciones trigonométricas son verdaderas para todos los ángulos y se conocen como las identidades trigonométricas. Algunas identidades equiparan una expresión a una expresión diferente que involucra los mismos ángulos. Éstos se enumeran en Lista de las identidades trigonométricas. Identidades triángulo que se relacionan los lados y ángulos de un triángulo dado se enumeran a continuación.
En las siguientes identidades, A, B y C son los ángulos de un triángulo y un, byc son las longitudes de los lados del triángulo frente a los respectivos ángulos.
Ley de los senos
La ley de los senos (también conocido como el "teorema del seno") para una arbitrarias estados triángulo:
donde R es el radio de la círculo circunscrito del triángulo:
Otra ley que implica senos se puede utilizar para calcular el área de un triángulo. Dados dos lados y el ángulo entre los lados, el área del triángulo es:
Ley de los cosenos
La ley de los cosenos (conocido como la fórmula del coseno, o la "regla cos") es una extensión del teorema de Pitágoras a los triángulos arbitrarios:
o equivalentemente:
Ley de las tangentes
La ley de las tangentes:
La fórmula de Euler
La fórmula de Euler, que establece que 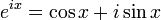 , Produce los siguientes analíticas identidades de seno, coseno y tangente en términos de electrónico y la unidad imaginaria i:
, Produce los siguientes analíticas identidades de seno, coseno y tangente en términos de electrónico y la unidad imaginaria i:


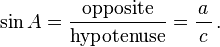
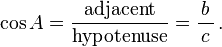
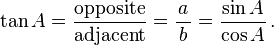
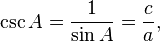
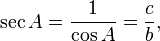
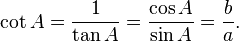
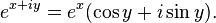
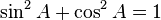
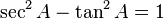
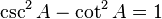
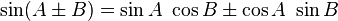
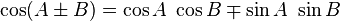
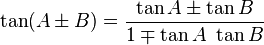
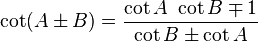
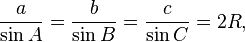
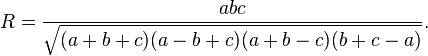
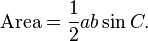
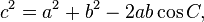
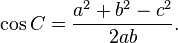
![\ Frac {ab} {a + b} = \ frac {\ tan \ left [\ tfrac {1} {2} (AB) \ right]} {\ tan \ left [\ tfrac {1} {2} (A + B) \ right]}](../../images/2161/216156.png)