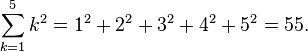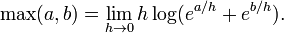Addition

3 + 2 = 5 avec des pommes , un choix populaire dans les manuels scolaires

L'addition est un opération mathématique qui représente la quantité totale d'objets entre eux dans une collection. Il est signifié par le signe plus (+). Par exemple, dans l'image sur la droite, il ya 3 + 2 pommes intentionnés trois pommes et deux pommes ensemble, ce qui est un total de 5 pommes. Par conséquent, 3 + 2 = 5. Outre les fruits de comptage, plus peut également représenter combinant d'autres grandeurs physiques et abstraites utilisant différents types de nombres: nombres négatifs , des fractions , des nombres irrationnels , des vecteurs , des décimales et plus.

Outre suit plusieurs tendances importantes. Il est commutative , ce qui signifie que l'ordre n'a pas d'importance, et il est associative , ce qui signifie que lorsque l'on ajoute plus de deux chiffres, ordre dans lequel addition est effectuée n'a pas d'importance (voir Sommation). Addition répétée de 1 est la même que compter; plus de 0 ne change pas un numéro. Outre obéit aussi à des règles prévisibles concernant des opérations connexes telles que la soustraction et la multiplication . Toutes ces règles peut être prouvé , à commencer par l'ajout de nombres naturels et la généralisation à travers les nombres réels et au-delà. Général opérations binaires qui continuent ces modèles sont étudiés dans l'algèbre abstraite .

Exécution plus est l'une des tâches les plus simples numériques. L'addition d'un très petit nombre est accessible à tout-petits; la tâche la plus fondamentale, 1 + 1, peut être réalisée par des enfants aussi jeunes que cinq mois et même quelques animaux. Dans l'enseignement primaire , les élèves ont appris à ajouter des numéros dans la décimale système, en commençant par un seul chiffre et de se attaquer progressivement des problèmes plus difficiles. Les aides mécaniques vont de l'ancien abaque au moderne ordinateur , où la recherche sur les implémentations les plus efficaces de l'addition continue à ce jour.

Notation et la terminologie

L'addition est écrit en utilisant la signe plus «+» entre les termes; ce est-à notation infixée. Le résultat est exprimé avec une signe égal. Par exemple,

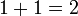(Verbalement, "un plus un égale deux")

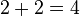(Verbalement, «deux plus deux font quatre»)

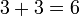(Verbalement, "trois plus trois égalent six")

(Voir «associativité» ci-dessous )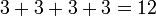

(Voir «multiplication» ci-dessous )

Il ya aussi des situations où l'addition est "entendu" même si aucun symbole ne apparaît:

Outre Colonnes:
5 + 12 = 17

• Une colonne de chiffres, avec le dernier numéro dans la colonne soulignée, indique généralement que les chiffres de la colonne doivent être ajoutés, avec la somme écrite en dessous du numéro souligné.
• Un nombre entier immédiatement suivie par une fraction indique la somme des deux, appelé un nombre fractionnaire. Par exemple,
  3½ = 3 + ½ = 3,5.
  Cette notation peut causer de la confusion puisque dans la plupart des autres contextes juxtaposition représente multiplication place.

La somme de a série de chiffres connexes peut être exprimée à travers notation sigma capital, ce qui dénote compacte itération. Par exemple,

Les numéros ou les objets à ajouter en plus générale sont appelés les termes, les opérandes, ou les opérandes; cette terminologie se répercute sur la somme de plusieurs termes. Ceci est à distinguer de facteurs, qui sont multipliées . Certains auteurs appellent le premier terme cumulande. En fait, au cours de la Renaissance , de nombreux auteurs ne ont pas considéré le premier terme un «addend" du tout. Aujourd'hui, en raison de la propriété commutative de l'addition, "cumulande" est rarement utilisé, et les deux termes sont généralement appelé opérandes.

Tout cela découle de la terminologie latine . " Addition "et" ajouter "sont Anglais mots dérivés du latin addere verbe, qui est à son tour un composé de l'annonce "pour" et oser «donner», de la Proto-racine indo-européenne * deh₃- «donner»; donc à ajouter est de donner à. En utilisant le adjectif verbal Les résultats de suffixe en "addend", "chose à ajouter". De même à partir augere "pour augmenter", on obtient "cumulande", "chose à être augmentée".

Redessiné illustration de l'art de Nombryng, l'un des premiers textes arithmétiques Anglais, au 15ème siècle

"Somme" et "summand" dérivent du latin substantif summa "le plus haut, le haut» et summare verbe associé. Ceci est approprié non seulement parce que la somme de deux nombres positifs est supérieur soit, mais parce qu'il était autrefois courant d'ajouter à la hausse, contrairement à la pratique moderne de l'ajout à la baisse, de sorte que la somme était littéralement plus élevé que les opérandes. Addere et summare remontent au moins à Boèce, si ce ne est aux écrivains romains antérieurs, tels que Vitruve et Frontin; Boethius également utilisé plusieurs autres conditions pour l'opération d'addition. Le plus tard Moyen terme anglais "adden" et "ajouter" ont été popularisée par Chaucer .

Interprétations

L'addition est utilisée pour modéliser innombrables processus physiques. Même pour le cas simple d'ajouter des nombres naturels , il ya beaucoup d'interprétations possibles et même des représentations plus visuels.

Combinant ensembles

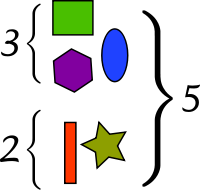
Peut-être l'interprétation la plus fondamentale de l'addition réside dans la combinaison des ensembles:

• Lorsque deux ou plusieurs collections disjoints sont combinés en une seule collection, le nombre d'objets de la collection unique est la somme du nombre d'objets dans les collections originales.

Cette interprétation est facile de visualiser, avec peu de risque d'ambiguïté. Il est également utile dans les mathématiques supérieures; pour le définition rigoureuse qu'elle inspire, voir numéros naturelles ci-dessous. Cependant, il ne est pas évident de savoir comment il faut étendre cette version de plus d'inclure des nombres fractionnaires ou nombres négatifs.

Une solution possible est de considérer des collections d'objets qui peuvent être facilement divisés, tels que tartes ou, mieux encore, segmenté tiges. Plutôt que de simplement combiner des collections de segments, les tiges peuvent être reliées bout-à-bout, qui illustre une autre conception de plus: l'addition, mais non les tiges les longueurs des tiges.

Étendant sur une longueur

Une deuxième interprétation de plus vient d'étendre une longueur initiale par une longueur donnée:

• Lorsque la durée d'origine est prolongée par une quantité donnée, la longueur finale est la somme de la longueur d'origine et la longueur de l'extension.

Une visualisation numéro en ligne de l'addition algébrique 2 + 4 = 6. Une traduction de 2 suivi par une traduction de 4 est le même que la traduction par six.

Une visualisation numéro en ligne de la plus unaire 2 + 4 = 6. Une traduction par 4 est équivalente à quatre traductions par une.

La somme a + b peut être interprété comme un opération binaire qui combine a et b, dans un sens algébrique, ou il peut être interprété comme l'ajout de b plusieurs unités à un. En vertu de la seconde interprétation, les parties d'une somme a + b jouent des rôles asymétriques, et l'opération a + b est considérée comme l'application de la opération unaire + b à un. Au lieu d'appeler à la fois un et opérandes b, il est plus approprié d'appeler un cumulande dans ce cas, car un joue un rôle passif. La vue unaire est également utile lors de l'examen de soustraction , car chaque opération d'addition unaire a une opération de soustraction unaire inverse, et vice versa.

Propriétés

Commutativité

4 + 2 = 2 + 4 avec des blocs

L'addition est commutative , ce qui signifie que l'on peut inverser les termes dans une somme de gauche à droite, et le résultat est le même que la dernière. Symboliquement, si a et b sont deux nombres, puis

a + b = b + a.

Le fait que l'addition est commutative est connue comme la "loi commutative de l'addition". Cette phrase suggère qu'il existe d'autres lois commutatives: par exemple, il ya une loi commutative de la multiplication. Cependant, beaucoup opérations binaires ne sont pas commutative, comme soustraction et la division, il est trompeur de parler d'une "loi commutative" sans réserve.

Associativité

2 + (1 + 3) = (2 + 1) 3 avec des tiges segmentées

Une propriété peu subtile de l'addition est associativité , qui arrive quand on essaie de définir addition répétée. Si l'expression

"A + b + c"

être défini comme signifiant (a + b) + c ou + (b + c)? Que l'addition est associative nous dit que le choix de la définition ne est pas pertinent. Pour toutes les trois nombres a, b et c, il est vrai que

(A + b) + c = a + (b + c).

Par exemple, (1 + 2) + 3 + 3 = 3 = 6 + 1 = 5 + 1 = (2 + 3). Toutes les opérations ne sont pas associatives, donc dans les expressions avec d'autres opérations comme la soustraction, il est important de spécifier le ordre des opérations.

élément d'identité

5 + 0 = 5 avec des sacs de points

Lors de l'ajout de zéro à un nombre quelconque, la quantité ne change pas; zéro est le élément neutre pour l'addition, également connu sous le nom identité additive. En symboles, pour tout un,

a + 0 = 0 + a = a.

Cette loi a été identifié en Brahmagupta de Brahmasphutasiddhanta en 628 AD, mais il l'a écrit que trois lois distinctes, selon que A est négatif, positif, ou zéro lui-même, et il a utilisé des mots plutôt que des symboles algébriques. Plus tard Mathématiciens indiens raffinés du concept; autour de l'an 830, Mahavira a écrit, «zéro devient le même que ce qui est ajouté à elle", correspondant à la déclaration unaire 0 + a = a. Au 12ème siècle, Bhaskara a écrit: «Dans l'ajout de chiffrement, ou la soustraction de celui-ci, la quantité, positif ou négatif, reste la même", correspondant à la déclaration unaire a + 0 = a.

Successeur

Dans le contexte d'entiers, l'addition d' une joue également un rôle particulier: pour tout entier a, le nombre entier (a + 1) est le plus petit entier supérieur à un, également connu comme le successeur d'un. Du fait de cette succession, la valeur de a + b certains peut également être considérée comme la 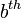successeur d'un, ce qui rend plus succession réitéré.

Unités

Pour ajouter numériquement grandeurs physiques avec unités, ils doivent d'abord être exprimées avec des unités communes. Par exemple, si une mesure de 5 pieds est prolongée par deux pouces, la somme est de 62 pouces, 60 pouces depuis est synonyme de 5 pieds. D'autre part, il est généralement inutile d'essayer d'ajouter trois mètres et 4 mètres carrés, puisque ces unités sont incomparables; ce genre de considération est fondamental dans analyse dimensionnelle.

Outre Performing

Capacité innée

Les études sur le développement des mathématiques à partir autour des années 1980 ont exploité le phénomène de accoutumance: nourrissons regardent plus à des situations qui sont inattendus. Une expérience séminale par Karen Wynn en 1992 dans Mickey Mouse poupées manipulées derrière un écran démontré que cinq mois nourrissons âgés attendent 1 + 1 à 2, et ils sont relativement surpris quand une situation physique semble impliquer que 1 + 1 est soit 1 ou 3. Ce résultat a été confirmé depuis par divers laboratoires utilisant des méthodologies différentes. Une autre expérience 1992 avec les anciens les tout-petits, de 18 à 35 mois, exploitées leur développement du contrôle moteur en leur permettant de récupérer de ping-pong balles d'une case; le plus jeune a répondu bien pour un petit nombre, alors que les sujets âgés étaient en mesure de calculer les sommes jusqu'à cinq.

Même certains animaux non humains montrent une capacité limitée d'ajouter, en particulier primates. Dans une expérience imitant 1995 1992 Résultat de Wynn (mais en utilisant aubergines au lieu de poupées), macaques rhésus et tamarins linaigrette une performance similaire à des nourrissons humains. Plus spectaculaire, après avoir appris la signification des chiffres arabes de 0 à 4, une chimpanzé était en mesure de calculer la somme des deux chiffres sans autre formation.

Découvrir plus que les enfants

Typiquement, les enfants d'abord maîtriser compter. Quand donné un problème qui nécessite que deux points et trois points soient combinés, les jeunes enfants modéliser la situation avec des objets physiques, souvent les doigts ou un dessin, puis comptent total. Comme ils acquièrent de l'expérience, ils apprennent ou découvrir la stratégie de «compter sur»: a demandé de trouver deux plus trois, les enfants comptent 02h03, en disant "trois, quatre, cinq" (généralement cochant doigts), et d'arriver à cinq . Cette stratégie semble presque universelle; les enfants peuvent facilement ramasser des pairs ou des enseignants. La plupart découvrent indépendamment. Avec une expérience supplémentaire, les enfants apprennent à ajouter plus rapidement en exploitant la commutativité de l'addition en comptant à partir du plus grand nombre, dans ce cas, à partir de trois ans et compter "quatre, cinq." Finalement, les enfants commencent à rappeler certains faits d'addition (" obligations numériques "), soit par l'expérience ou la mémorisation. Une fois que certains faits sont commis à la mémoire, les enfants commencent à tirer des faits inconnus de ceux connus. Par exemple, un enfant a demandé d'ajouter six et sept peuvent savoir que 6 + 6 = 12 et alors la raison que 6 + 7 est un de plus, ou 13. Ces faits dérivés peuvent être trouvés très rapidement et élève de l'école la plus élémentaire éventuellement se appuient sur un mélange de faits mémorisés et dérivés pour ajouter couramment.

Système décimal

La condition préalable à l'addition dans la décimale système est couramment le rappel ou la dérivation des «faits d'addition" 100 à un seul chiffre. On pourrait mémoriser tous les faits par stratégies rote, mais basée sur des modèles sont plus instructif et, pour la plupart des gens, plus efficace:

• Commutativité: mentionnés ci-dessus, en utilisant le modèle a + b = b + a réduit le nombre de «faits d'addition" 100-55.
• Un ou deux de plus: Ajout de 1 ou 2 est une tâche de base, et il peut être accompli par comptage ou, finalement, intuition.
• Zero: Depuis zéro est l'identité d'additif, ajoutant zéro est trivial. Néanmoins, dans l'enseignement de l'arithmétique, certains élèves sont initiés à plus comme un processus qui augmente toujours les opérandes; problèmes de mots peuvent aider à rationaliser l '«exception» de zéro.
• Doubles: Ajout d'un numéro à lui-même est liée à compter par deux et de multiplication . Doubles faits forment une épine dorsale pour de nombreux faits connexes, et les étudiants les trouvent relativement facile à saisir.
• Proche-doubles: Sommes tels que 6 + 7 = 13 peuvent être rapidement origine dans le fait doubles 6 + 6 = 12 en ajoutant un de plus, ou à partir de 7 + 7 = 14, mais une soustraction.
• Cinq et dix: Les sommes de la forme 5 + 10 + x et x sont généralement mémorisé début et peut être utilisé pour dériver d'autres faits. Par exemple, 6 + 7 = 13 peut être dérivé de 5 + 7 = 12 par addition d'une plus.
• Faire dix: Une stratégie avancée utilise 10 comme intermédiaire pour des sommes impliquant 8 ou 9; par exemple, 8 + 6 = 8 + 2 + 4 + 4 = 10 = 14.

Comme les élèves grandissent, ils commettent plus de faits à la mémoire, et apprennent à tirer rapidement et couramment d'autres faits. Beaucoup d'étudiants ne se engagent tous les faits à la mémoire, mais peuvent encore trouver un fait de base rapidement.

L'algorithme standard pour ajouter des numéros de plusieurs chiffres est d'aligner les opérandes verticalement et ajouter les colonnes, à partir de la colonne des unités sur la droite. Si une colonne dépasse dix, le chiffre supplémentaire est " réalisée »dans la colonne suivante Une autre stratégie commence ajoutant du chiffre le plus significatif sur la gauche;.. cette route permet de transporter un peu maladroit, mais il est plus rapide à obtenir une estimation approximative de la somme Il ya beaucoup d'autres méthodes alternatives.

• Fraction: Addition
• La notation scientifique: Opérations

Ordinateurs

Addition avec un ampli-op. Voir Amplificateur de sommation pour plus de détails.

Les ordinateurs analogiques travaillent directement avec des quantités physiques, de sorte que leurs mécanismes d'addition dépendent de la forme des opérandes. Une extension de mécanique pourrait représenter deux opérandes que les positions des blocs coulissants, auquel cas ils peuvent être ajoutés avec une moyenne levier. Si les opérandes sont les vitesses de rotation des deux arbres, ils peuvent être ajoutés avec un différentiel. Une extension hydraulique peut ajouter le les pressions dans les deux chambres par l'exploitation de la seconde loi de Newton pour équilibrer les forces sur un assemblage de pistons. La situation la plus courante pour un ordinateur à usage général analogique consiste à ajouter deux tensions (par rapport à sol); ceci peut être réalisé avec une plus ou moins résistance réseau, mais une meilleure conception exploite une amplificateur opérationnel.

L'addition est également fondamentale pour le fonctionnement des calculateurs numériques , où l'efficacité de l'addition, en particulier le effectuer mécanisme, est une limitation importante à la performance globale.

Partie de Charles Babbage Difference Engine y compris l'ajout et de mener des mécanismes

Ajout de machines, calculatrices mécaniques dont la fonction première était plus, ont été les premiers, les ordinateurs numériques automatiques. 1623 Horloge Calcul de Wilhelm Schickard pourrait additionner et soustraire, mais il a été sévèrement limitée par un mécanisme de report maladroit. Brûlé lors de sa construction en 1624 et inconnu dans le monde pendant plus de trois siècles, il a été redécouvert en 1957 et ne avait donc pas d'impact sur le développement des calculatrices mécaniques. Blaise Pascal a inventé la calculatrice mécanique en 1642 avec un mécanisme de report Assisted Gravity-ingénieuse . Pascaline a été limitée par son mécanisme de report dans un sens différent: ses roues tourné qu'une seule façon, il pourrait ajouter mais pas soustraire, sauf par le Procédé de compléments. En 1674 Gottfried Leibniz a fait le premier multiplicateur mécanique; il a été toujours sous tension, si ce ne est motivé, par addition.

" Circuit additionneur complet "logique qui ajoute deux chiffres binaires A et B, avec une entrée de report _en C, produisant le bit de somme, S, et une sortie de report, C _out.

Additionneurs exécutent plus entier dans les ordinateurs numériques électroniques, généralement en utilisant l'arithmétique binaire . L'architecture la plus simple est l'additionneur de report en cascade, qui suit l'algorithme à plusieurs chiffres standard. Une légère amélioration est le transporter Conception saut, de nouveau après l'intuition humaine; on ne effectue pas tous les porte dans le calcul de 999 + 1, mais on contourne le groupe de 9s et saute à la réponse.

Comme ils calculent chiffres un par un, les procédés ci-dessus sont trop lentes pour la plupart des applications modernes. Dans les ordinateurs numériques modernes, plus entier est généralement l'instruction la plus rapide de l'arithmétique, mais il a le plus grand impact sur les performances, car elle sous-tend tous les opérations en virgule flottante ainsi que des tâches aussi fondamentales que répondre génération cours accès à la mémoire et la récupération l'instruction, pendant ramification. Pour augmenter la vitesse, des conceptions modernes calculent en chiffres parallèle; ces régimes vont par des noms tels que mener sélectionnez, effectuer anticipation et le Pseudocarry Ling. Presque toutes les implémentations modernes sont, en fait, des hybrides de ces trois dernières conceptions.

Contrairement plus sur papier, outre sur un ordinateur change souvent les opérandes. Sur l'ancienne boulier et carte ajoutant, les deux opérandes sont détruites, laissant seulement la somme. L'influence de l'abaque sur la pensée mathématique était assez fort que les premiers latine textes souvent affirmé que dans le processus d'ajouter "un certain nombre à un chiffre", les deux numéros disparaissent. Dans les temps modernes, l'instruction ADD d'un microprocesseur remplace la cumulande avec la somme mais conserve le cumulateur. Dans un langage de programmation de haut niveau, l'évaluation a + b ne change pas a ou b; si le but est de remplacer un à la somme doit être explicitement cette demande, typiquement avec l'énoncé a = a + b. Certains langages tels que C ou C ++ permettent de porter un abrégé en a + b =.

Addition des nombres naturels et réels

Pour prouver les propriétés habituelles de plus, il faut d'abord définir plus pour le contexte en question. L'addition est d'abord défini sur les nombres naturels . En théorie des ensembles , plus est ensuite progressivement étendu à de plus grands ensembles qui comprennent les nombres naturels: les nombres entiers , les nombres rationnels et les nombres réels . (Dans l'enseignement des mathématiques, des fractions positives sont ajoutés avant les nombres négatifs sont même considérées; ce est aussi la route historique)

Nombres naturels

Il ya deux façons populaires pour définir la somme de deux nombres naturels a et b. Si l'on définit des nombres naturels pour être les cardinalités des ensembles finis, (le cardinal d'un ensemble est le nombre d'éléments de l'ensemble), il convient de définir leur somme comme suit:

• Soit N (S) le cardinal d'un ensemble S. Prendre deux ensembles disjoints A et B, avec N (A) = A et N (B) = b. Ensuite, a + b est définie comme .

Ici, A U B est le union de A et B. Une autre version de cette définition permet A et B se chevauchent éventuellement et prend alors leur union disjointe, un mécanisme qui permet aux éléments communs à être séparées et donc comptés deux fois.

L'autre définition populaire est récursive:

• Soit n ⁺ être le successeur de n, ce est le nombre n dans la suite des nombres naturels, de sorte que 0 = ⁺ 1, ⁺ 1 = 2. Définir un + 0 = a. Définir la somme récursive en général a + (b ⁺⁾ = (a + b) ^+. D'où 1 + 1 = 1 + 0 ⁺ = (1 + 0) ⁺ = ⁺ 1 = 2.

Encore une fois, il existe des variations mineures sur cette définition dans la littérature. Pris à la lettre, la définition ci-dessus est une application de la Recursion théorème sur le poset N ^2. D'autre part, certaines sources préfèrent utiliser un théorème Recursion restreint qui se applique uniquement à l'ensemble des nombres naturels. On considère alors d'être temporairement "fixe", se applique récurrence sur b pour définir une fonction "a +", et pâtes de ces opérations unaires pour tous un ensemble pour former l'opération binaire complet.

Cette formulation récursive de plus a été développé par Dedekind dès 1854, et il serait élargir dans les décennies suivantes. Il a prouvé les propriétés associatives et commutatives, entre autres, par le biais induction mathématique; des exemples de ces démonstrations inductives, voir Addition des nombres naturels .

Entiers

Définition (-2) + 1 en utilisant seulement l'addition de nombres positifs: (2-4) + (3-2) = 5-6.

La conception la plus simple d'un nombre entier, ce est qu'il se compose d'une valeur absolue (qui est un nombre naturel) et un signer (généralement soit positive ou négative ). Le nombre entier zéro est un troisième cas particulier, ne étant ni positif ni négatif. La définition correspondante de l'addition doit procéder par cas:

• Pour un entier n, soit | n | être sa valeur absolue. Soient a et b des entiers. Si a ou b est égal à zéro, le traiter comme une identité. Si A et B sont tous deux positifs, de définir a + b = | a | + | b |. Si a et b sont tous deux négatifs, définir un + b = - (| a | + | b |). Si A et B ont des signes différents, a + b définie comme étant la différence entre | a | et | b |, avec le signe du terme dont la valeur absolue est plus grande.

Bien que cette définition peut être utile pour des problèmes concrets, il est beaucoup trop compliqué à produire des épreuves générales élégantes; il ya trop de cas à considérer.

Une conception beaucoup plus pratique des entiers est le La construction de groupe de Grothendieck. L'observation essentielle est que tout entier peut être exprimé (non unique) comme la différence de deux nombres naturels, alors on peut ainsi définir un nombre entier comme la différence de deux nombres naturels. L'addition est alors définie pour être compatible avec la soustraction:

• Etant donné deux nombres entiers a - b et c - d, où a, b, c, et d sont des nombres naturels, définir (a - b) + (c - d) = (a + c) - (b + d).

Nombres rationnels (fractions)

L'addition de nombres rationnels peut être calculée en utilisant la dénominateur commun moins, mais une définition conceptuellement plus simple implique que plus entière et la multiplication:

• Définir

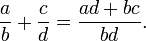
La commutativité et l'associativité des plus rationnelle est une conséquence facile des lois de l'arithmétique entier. Pour une discussion plus rigoureuse et plus général, voir corps des fractions.

Nombres réels

Ajout π ^2/6 e et en utilisant des coupes de Dedekind rationnels

Une construction commune de l'ensemble des nombres réels est l'achèvement Dedekind de l'ensemble des nombres rationnels. Un nombre réel est défini comme étant un Dedekind coupe de rationnels: un ensemble non vide des rationnels qui est fermée à la baisse et n'a pas plus grand élément. La somme des nombres réels a et b est défini élément par élément:

• Définir

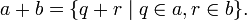
Cette définition a été publié, sous une forme légèrement modifiée, par Richard Dedekind en 1872. La commutativité et l'associativité de biens sont plus immédiate; définir le nombre réel de 0 à l'ensemble des rationnels négatifs, il est facile de voir que la dénomination additif. Probablement la partie la plus délicate de cette construction, relatifs à l'addition est la définition des inverses additifs.

Ajout π ^2/6 e et en utilisant des séquences de Cauchy rationnels

Malheureusement, face à la multiplication des coupures de Dedekind est un cauchemar cas par cas similaire à l'addition des entiers signés. Une autre approche est l'achèvement métrique des nombres rationnels. Un nombre réel est essentiellement défini comme la limite d'un Cauchy des rationnels, lim a _n. L'addition est définie terme à terme:

• Définir

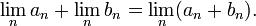
Cette définition a été publié par Georg Cantor , également en 1872, bien que son formalisme était légèrement différente. Il faut prouver que cette opération est bien défini, traitant avec des séquences co-Cauchy. Une fois cette tâche terminée, toutes les propriétés de plus réel suivent immédiatement les propriétés des nombres rationnels. En outre, les autres opérations arithmétiques, y compris la multiplication, ont simples, des définitions analogues.

Généralisations

Il ya beaucoup de choses qui peuvent être ajoutés: des chiffres, des vecteurs, des matrices, des espaces, des formes, des ensembles, des fonctions, des équations, cordes, chaînes ... - Alexander Bogomolny

Il ya de nombreuses opérations binaires qui peuvent être considérés comme des généralisations de l'opération d'addition sur les nombres réels. Le domaine de l'algèbre abstraite telle importance à ces opérations généralisées, et ils apparaissent également dans la théorie des ensembles et théorie des catégories.

Addition en algèbre abstraite

En algèbre linéaire , un espace vectoriel est une structure algébrique qui permet d'ajouter deux quelconques vecteurs et pour l'extension des vecteurs. Un espace vectoriel familier est l'ensemble de toutes les paires ordonnées de nombres réels; le couple (a, b) est interprété comme un vecteur partir de l'origine dans le plan euclidien au point (a, b) dans le plan. La somme des deux vecteurs est obtenu en ajoutant leurs coordonnées individuelles:

(A, b) + (c, d) = (a + c, b + d).

Cette opération d'addition est au cœur de la mécanique classique , dans lequel les vecteurs sont interprétés comme des forces .

En arithmétique modulaire , l'ensemble des entiers modulo 12 a douze éléments; il hérite une opération d'addition des nombres entiers qui est au cœur de la théorie des ensembles de musique. L'ensemble des entiers modulo 2 a seulement deux éléments; l'opération d'addition, il est connu dans hérite logique booléenne comme le " exclusive ou de la fonction ". En géométrie , la somme de deux mesures d'angle est souvent considéré comme leur somme comme des nombres réels modulo 2π. Cela revient à une opération d'addition sur le cercle , qui à son tour se généralise à des opérations d'addition sur plusieurs dimensions tori .

La théorie générale de l'algèbre abstraite permet une opération "ajout" d'être toute associative et commutative opération sur un ensemble. Base structures algébriques avec une telle opération d'addition comprennent monoïdes commutatifs et groupes abéliens.

Outre la théorie des ensembles et la théorie des catégories

Une généralisation de grande envergure de plus des nombres naturels est l'addition de nombres ordinaux et nombres cardinaux dans la théorie des ensembles. Ceux-ci donnent deux généralisations différentes d'addition des nombres naturels à la transfinite. Contrairement à la plupart des opérations d'addition, l'addition de nombres ordinaux ne est pas commutative. L'addition de nombres cardinaux, cependant, est une opération commutative étroitement liée à la opération d'union disjointe.

En la théorie des catégories, union disjointe est considéré comme un cas particulier de la opération de co-produit et co-produits généraux sont peut-être la plus abstraite de toutes les généralisations de plus. Certains co-produits, tels que Somme directe et Bouquet, sont nommés pour évoquer leur connexion avec l'addition.

Les opérations connexes

Arithmétique

Soustraction peut être considéré comme une sorte d'addition, ce est-addition d'un Opposé. Soustraction est lui-même une sorte de inverse de plus, en ce que x et x ajoutant soustraction sont des fonctions inverses .

Étant donné un ensemble avec une opération d'addition, on ne peut pas toujours définir une opération de soustraction correspondante sur cet ensemble; l'ensemble des nombres naturels est un exemple simple. D'autre part, une opération de soustraction unique détermine une opération d'addition, une opération inverse de l'additif, et une identité d'additif; pour cette raison, un groupe additif peut être décrit comme un ensemble qui est fermé sous la soustraction.

Multiplication peut être considéré comme plus répétée. Si un seul x terme apparaît dans une somme n fois, puis la somme est le produit de n et x. Si n ne est pas un nombre naturel , le produit peut encore un sens; par exemple, la multiplication par -1 Donne le inverse additif d'un nombre.

Une règle à calcul circulaire

Dans les nombres réels et complexes, addition et la multiplication peuvent être échangés par la fonction exponentielle :

e ^{a + b} = e ^un e ^b.

Cette identité permet à la multiplication effectuée par consultation d'un table des logarithmes et plus de calcul à la main; elle permet également une multiplication sur glisser règle. La formule est toujours une bonne approximation de premier ordre dans le contexte plus large de groupes de Lie, où il concerne la multiplication des éléments du groupe infinitésimales avec addition de vecteurs dans la associé Algèbre de Lie.

Il ya encore plus de la multiplication des généralisations que l'addition. En général, les opérations de multiplication toujours distribuer sur l'addition; cette exigence est formalisée dans la définition d'un anneau. Dans certains contextes, tels que les entiers, distributivité sur l'addition et l'existence d'une identité multiplicative est suffisant pour déterminer de manière unique l'opération de multiplication. La propriété distributive fournit également des informations sur plus; en développant le produit (1 + 1) (a + b) dans les deux sens, on conclut que l'addition est forcé d'être commutative. Pour cette raison, l'addition d'anneau est commutatif en général.

Division est une opération arithmétique à distance liée à l'addition. Depuis a / b = a (b ^-1), la division est distributive droit sur l'addition: (a + b) / c = a / c + b / c. Toutefois, la division ne est pas laissé distributive sur l'addition; 1 / (2 + 2) ne est pas la même que 1/2 + 1/2.

Commande

Déconnexion log de x + 1 et max (x, 1) de x = 0,001 à 1000

Le fonctionnement maximale "max (a, b)» est une opération binaire similaire à l'addition. En fait, si deux nombres non négatifs a et b sont différents de ordres de grandeur, puis leur somme est approximativement égale à leur maximum. Cette approximation est extrêmement utile dans les applications des mathématiques, par exemple dans tronquant série de Taylor . Cependant, il présente une difficulté perpétuelle analyse numérique, essentiellement depuis "max" ne est pas inversible. Si b est beaucoup plus qu'un, puis un simple calcul de (a + b) - b peut accumuler une inacceptable erreur d'arrondi, peut-être même le retour à zéro. Voir également La perte de signification.

Le rapprochement devient exacte dans une sorte de limite infinie; si a ou b est un infini nombre cardinal , leur somme cardinale est exactement égal au plus élevé des deux. En conséquence, il n'y a pas d'opération de soustraction pour cardinaux infinis.

Maximisation est commutative et associative, comme l'addition. En outre, puisque l'addition conserve l'ordre des nombres réels, outre distribue sur "max" de la même manière que la multiplication distribue sur l'addition:

a + max (b, c) = max (a + b, a + c).

Pour ces raisons, dans tropical géométrie remplace une multiplication par addition et addition avec maximisation. Dans ce contexte, plus est appelée «multiplication tropicale", la maximisation est appelé "plus tropicale", et la zone tropicale «identité additif» est l'infini négatif. Certains auteurs préfèrent remplacer addition avec réduction au minimum; puis l'identité additif est l'infini positif.

Lier ces observations ensemble, plus tropical est liée à environ plus régulière à travers le logarithme :

log (a + b) ≈ max (log a, log b),

qui devient plus précis que la base du logarithme augmente. Le rapprochement peut être fait exacte en extrayant une constante h , nommé par analogie avec la constante de Planck à partir de la mécanique quantique , et en prenant la " limite classique »comme h tend vers zéro:

En ce sens, le fonctionnement maximale est unedéquantifiéversion de l'addition.

Autres façons d'ajouter

Incrémentation, également connu sous le nomd'opération successeur, est l'addition d'uneforme de nombre.

Sommation décrit l'ajout d'un nombre arbitraire de chiffres, généralement plus que deux. Il comprend l'idée de la somme d'un nombre unique, lui-même, et la somme vide, qui est zéro . Une sommation infinie est une procédure délicate connue comme une série.

Compterun ensemble fini est équivalent à la somme 1 sur l'ensemble.

Intégration est une sorte de "sommation" sur un continuum, ou plus précisément et plus généralement, sur une différentiables collecteur . Intégration sur une variété de dimension zéro réduit à la somme.

Combinaisons linéaires se combinent multiplication et sommation; Ce sont les sommes dont chaque terme a un effet multiplicateur, habituellement un réel ou complexe numéro. Combinaisons linéaires sont particulièrement utiles dans des contextes où plus simple violerait une règle de normalisation, tels que le mélange de stratégies dans la théorie des jeux ou de superposition des états à la mécanique quantique .

Convolution est utilisé pour ajouter deux indépendants des variables aléatoires déterminées par des fonctions de distribution . Sa définition habituelle combine intégration, la soustraction, la multiplication et. En général, la convolution est utile comme une sorte d'addition domaine à côte; En revanche, l'addition de vecteur est un type de gamme addition à côte.

Dans la littérature

• Dans le chapitre 9 de Lewis Carroll De l'autre côté du miroir , la Reine Blanche demande Alice, "et vous ne Addition? ... Quel est un et un et un et un et un et un et un et un et un et un?" Alice avoue qu'elle a perdu le compte, et la Reine Rouge déclare, "Elle ne peut pas faire Addition".
• En De George Orwell Nineteen Eighty-Four , la valeur de 2 + 2 est remis en question; l'État soutient que si elle déclare 2 + 2 = 5, alors il en est ainsi. Voir Deux plus deux font cinq pour l'histoire de cette idée.