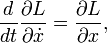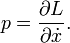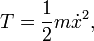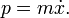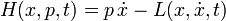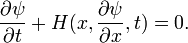Calcul des variations
Renseignements généraux
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. parrainage SOS enfant est cool!
Calcul des variations est un champ de mathématiques qui traite extremizing fonctionnelles, par opposition à ordinaire calcul qui traite des fonctions . Un fonctionnelle est généralement une cartographie à partir d'un ensemble de fonctions pour les nombres réels. Fonctionnels sont souvent formés comme intégrales définies impliquant des fonctions inconnues et leurs dérivés. L'intérêt est dans les fonctions extrêmes qui rendent les fonctionnelle atteindre une valeur maximum ou minimum - ou fonctions fixes - ceux où le taux de variation de la fonctionnelle est précisément zéro.
Peut-être l'exemple le plus simple d'un tel problème est de trouver la courbe de longueur plus courte, ou géodésiques, reliant deux points. Se il n'y a pas de contraintes, la solution est évidemment une ligne droite entre les points. Cependant, si la courbe est astreinte à se situer sur une surface dans l'espace, puis la solution est moins évidente, et peut-être de nombreuses solutions peuvent exister. De telles solutions sont connues sous le nom géodésiques. Un problème connexe est posé par Principe de Fermat: la lumière suit le trajet optique de longueur la plus courte reliant deux points, où la longueur optique dépend du matériau du support. Un concept correspondant dans mécanique est le principe de moindre action.
Beaucoup de problèmes importants impliquent fonctions de plusieurs variables. Solutions de problèmes aux limites pour le L'équation de Laplace satisfaire Principe de Dirichlet. Problème de Plateau, il faut trouver une surface de superficie minimale qui se étend sur un contour donné dans l'espace: la ou les solutions peuvent souvent être trouvées par trempage d'un fil de fer dans une solution d'eau savonneuse. Bien que de telles expériences sont relativement faciles à exécuter, leur interprétation mathématique est loin d'être simple: il peut y avoir plus d'une surface minimisant localement, et ils peuvent avoir topologie non triviale.
Histoire
Le calcul des variations peut être dit de commencer par un problème de Johann Bernoulli de (1696). Il a immédiatement occupé l'attention des Jakob Bernoulli et la Marquis de l'Hôpital, mais Euler abord élaboré le sujet. Ses contributions ont commencé en 1733, et son Elementa Calculi Variationum donné à la science son nom. Lagrange a largement contribué à la théorie, et Legendre (1786) a défini une méthode, pas entièrement satisfaisant, pour la discrimination des maxima et minima. Newton et Leibnitz ont aussi donné une certaine attention tôt pour le sujet. Pour cette discrimination Brunacci (1810), Gauss (1829), Poisson (1831), Ostrogradsky (1834), et Jacobi (1837) ont été parmi les contributeurs. Un travail général important est celui de Sarrus (1842) qui a été condensée et améliorée par Cauchy (1844). Autres traités et les mémoires de valeur ont été écrit par Strauch (1849), Jellett (1850), Hesse (1857), Clebsch (1858), et Carll (1885), mais peut-être le travail le plus important du siècle est celui de Weierstrass. Son célèbre cours sur la théorie est epoch-making, et on peut affirmer qu'il était le premier à le placer sur une base solide et incontestable. Le 20 et le 23 Problèmes de Hilbert publiés en 1900 attirés développement. Au 20e siècle Hilbert , Noether, Tonelli, Lebesgue et HADAMARD entre autres fait des contributions importantes. Marston Morse calcul des variations appliqué dans ce qu'on appelle maintenant La théorie de Morse. Pontryagin, Rockafellar et Clarke a développé de nouveaux outils mathématiques pour théorie du contrôle optimal, une généralisation du calcul des variations.
Extrema faibles et forts
Le supremum norme (également appelée norme infinie) pour fonctions réelles, continues, bornés sur un espace topologique 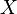 est défini comme étant
est défini comme étant
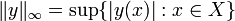 .
.
Un fonctionnelle 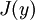 définie sur un espace approprié de fonctions
définie sur un espace approprié de fonctions 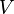 à la norme
à la norme 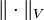 est dit d'avoir un minimum faible à la fonction
est dit d'avoir un minimum faible à la fonction 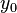 se il existe une certaine
se il existe une certaine 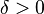 de telle sorte que, pour toutes les fonctions y avec
de telle sorte que, pour toutes les fonctions y avec 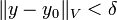 ,
,
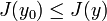 .
.
Maxima faibles sont définis de façon similaire, l'inégalité dans la dernière équation inversée. Dans la plupart des problèmes, 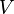 est l'espace des fonctions continûment dérivables de r sur un compact
est l'espace des fonctions continûment dérivables de r sur un compact 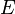 de la ligne réelle, avec sa norme donnée par
de la ligne réelle, avec sa norme donnée par
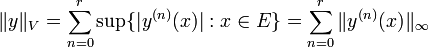 .
.
Cette norme ne est que la somme des normes de supremum de  et ses dérivés.
et ses dérivés.
Un fonctionnelle  est dit d'avoir une forte minimum
est dit d'avoir une forte minimum 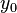 se il existe une certaine
se il existe une certaine 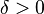 de telle sorte que, pour toutes les fonctions y avec
de telle sorte que, pour toutes les fonctions y avec 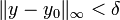 ,
, 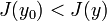 . Forte maximale est définie de manière similaire, mais avec l'inégalité dans la dernière équation inversée.
. Forte maximale est définie de manière similaire, mais avec l'inégalité dans la dernière équation inversée.
La différence entre les extrema forte et faible est que, pour une forte extremum, 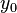 est un extremum local par rapport à l'ensemble de
est un extremum local par rapport à l'ensemble de 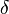 -Près fonctions par rapport à la norme de borne supérieure. En général, cette (sup) est norme différente de la norme
-Près fonctions par rapport à la norme de borne supérieure. En général, cette (sup) est norme différente de la norme 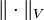 que V a été doté. Si
que V a été doté. Si 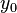 est une forte extremum pour
est une forte extremum pour 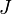 alors il est aussi un extremum faible, mais l'inverse ne peut détenir. Trouver forte extrema est plus difficile que de trouver faible extrema et dans ce qui suit, on supposera que nous cherchons faible extrema.
alors il est aussi un extremum faible, mais l'inverse ne peut détenir. Trouver forte extrema est plus difficile que de trouver faible extrema et dans ce qui suit, on supposera que nous cherchons faible extrema.
L'équation d'Euler-Lagrange
Dans des conditions idéales, les maxima et les minima d'une fonction donnée peuvent être situés en trouvant des points où sa dérivée se annule. Par analogie, des solutions de problèmes de variations lisses peuvent être obtenus par résolution de l'associé Équation d'Euler-Lagrange.
Considérons la fonctionnelle:
La fonction 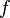 devrait avoir au moins un dérivé afin de satisfaire les exigences de demande valide de la fonction; en outre, si l'fonctionnel
devrait avoir au moins un dérivé afin de satisfaire les exigences de demande valide de la fonction; en outre, si l'fonctionnel ![A [f]](../../images/761/76192.png) atteint sa minimum local au
atteint sa minimum local au 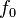 et
et 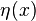 est une fonction arbitraire qui a au moins un dérivé et se annule aux extrémités
est une fonction arbitraire qui a au moins un dérivé et se annule aux extrémités 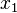 et
et 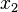 , Alors nous devons avoir
, Alors nous devons avoir
pour ne importe quel nombre ε proche de 0. Par conséquent, le dérivé de ![A [f_0 + \ epsilon \ eta]](../../images/761/76197.png) par rapport à ε (la première variante A) doit disparaître à ε = 0.
par rapport à ε (la première variante A) doit disparaître à ε = 0.
où nous avons utilisé la règle de la chaîne dans la deuxième ligne et intégration par parties dans le troisième. Le dernier terme de la troisième ligne disparaît parce 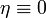 au niveau des points d'extrémité. Enfin, selon le lemme fondamental du calcul des variations, nous constatons que
au niveau des points d'extrémité. Enfin, selon le lemme fondamental du calcul des variations, nous constatons que 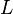 saura satisfaire l'équation d'Euler-Lagrange
saura satisfaire l'équation d'Euler-Lagrange
En général, cela donne un second ordre équation différentielle ordinaire qui peut être résolu pour obtenir le extremal 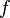 . L'équation d'Euler-Lagrange est un nécessaire, mais non suffisante, pour une extrémale. Des conditions suffisantes pour une extrémale sont discutés dans les références.
. L'équation d'Euler-Lagrange est un nécessaire, mais non suffisante, pour une extrémale. Des conditions suffisantes pour une extrémale sont discutés dans les références.
Afin d'illustrer ce processus, considérons le problème de trouver la courbe la plus courte dans le plan qui relie deux points 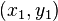 et
et 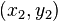 . Le longueur de l'arc est donnée par
. Le longueur de l'arc est donnée par
avec
et où 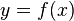 ,
, 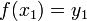 Et
Et 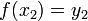 .
.
pour chaque choix de la fonction 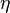 . On peut interpréter cette condition comme la disparition de tous des dérivées directionnelles
. On peut interpréter cette condition comme la disparition de tous des dérivées directionnelles ![A [f_0]](../../images/762/76209.png) en l'espace de fonctions différentiables, et cela est formalisé en exigeant que le Dérivé de Fréchet
en l'espace de fonctions différentiables, et cela est formalisé en exigeant que le Dérivé de Fréchet  à disparaître au
à disparaître au 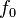 . Si nous supposons que
. Si nous supposons que 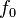 a deux dérivées continues (ou si l'on considère dérivés faibles), alors nous peuvent utiliser intégration par parties:
a deux dérivées continues (ou si l'on considère dérivés faibles), alors nous peuvent utiliser intégration par parties:
avec la substitution
alors nous avons
mais le premier terme est nul car 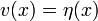 a été choisi à disparaître au
a été choisi à disparaître au 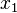 et
et 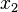 où l'évaluation est prise. En conséquence,
où l'évaluation est prise. En conséquence,
pour toute fonction deux fois dérivable 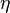 qui se annule aux extrémités de l'intervalle.
qui se annule aux extrémités de l'intervalle.
Nous pouvons maintenant appliquer la lemme fondamental du calcul des variations: Si
pour toute fonction suffisamment différentiable 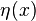 dans la plage d'intégration qui se annule aux extrémités de l'intervalle, il se ensuit que
dans la plage d'intégration qui se annule aux extrémités de l'intervalle, il se ensuit que 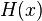 est identiquement nulle sur son domaine.
est identiquement nulle sur son domaine.
En conséquence,
Il résulte de ce que l'équation
et donc les extrémales sont des lignes droites.
L'identité Beltrami
Fréquemment, dans des problèmes physiques, il se avère que 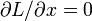 . Dans ce cas, l'équation d'Euler-Lagrange peut être simplifiée en utilisant le Beltrami identité:
. Dans ce cas, l'équation d'Euler-Lagrange peut être simplifiée en utilisant le Beltrami identité:
où 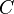 est une constante. Le côté gauche est le Transformation de Legendre de L par rapport à f '.
est une constante. Le côté gauche est le Transformation de Legendre de L par rapport à f '.
Le théorème de du Bois Reymond
Jusqu'ici, la discussion a supposé que les fonctions extrêmes possèdent deux dérivées continues, bien que l'existence de l'intégrale A nécessite seulement premières dérivées de fonctions d'essai. La condition que la première variation disparaître à une extrémale peut être considéré comme une forme faible de l'équation d'Euler-Lagrange. Le théorème de du Bois Reymond affirme que cette forme faible implique la forme forte. Si L a continues dérivées premières et secondes par rapport à l'ensemble de ses arguments, et si
puis 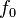 a deux dérivées continues, et il satisfait l'équation d'Euler-Lagrange.
a deux dérivées continues, et il satisfait l'équation d'Euler-Lagrange.
Fonctions de plusieurs variables
Variationnelles problèmes qui impliquent plusieurs intégrales se posent dans de nombreuses applications. Par exemple, si φ (x, y) désigne le déplacement d'une membrane au-dessus du domaine D dans le plan x, y, puis son énergie potentielle est proportionnelle à sa surface:
Le problème consiste à trouver Plateau une fonction qui minimise l'aire de surface tout en assumant des valeurs prescrites de la limite de D; les solutions sont appelées surfaces minimales. L'équation d'Euler-Lagrange pour ce problème est non linéaire:
Voir Courant (1950) pour plus de détails.
Principe de Dirichlet
Il est souvent suffisant de considérer que de faibles déplacements de la membrane, dont la différence d'énergie de déplacement ne est approximée par
Le V fonctionnelle doit être minimisée parmi toutes les fonctions d'essai φ qui supposent des valeurs prescrites sur le bord de D. Si u est la fonction de minimisation et V est une fonction lisse arbitraire qui se évanouit sur le bord de D, la première variation de ![V [u + \ epsilon v]](../../images/762/76225.png) doit disparaître:
doit disparaître:
Pourvu que u a deux dérivés, nous pouvons appliquer le théorème de la divergence d'obtenir
où C est la limite de D, S est arclength le long de C et 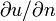 est la dérivée normale de u sur C. Depuis v et C se annule sur la première variation se annule, le résultat est
est la dérivée normale de u sur C. Depuis v et C se annule sur la première variation se annule, le résultat est
pour toutes les fonctions v lisse qui disparaissent à la limite de D. La preuve dans le cas d'une intégrales dimensions peut être adaptée à ce cas pour montrer que
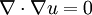 dans D.
dans D.
La difficulté avec ce raisonnement est l'hypothèse que la fonction de minimisation u doit avoir deux dérivés. Riemann a fait valoir que l'existence d'une fonction de minimisation lisse a été assurée par la connexion avec le problème physique:. Membranes ne assument effet configurations avec énergie potentielle minimale Riemann nommé ce principe de Dirichlet idée en l'honneur de son maître Dirichlet. Cependant Weierstrass a donné un exemple d'un problème variationnel sans solution: réduire
parmi toutes les fonctions φ qui satisfont 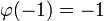 et
et 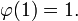 W peut être fait en choisissant arbitrairement petit fonctions linéaires par morceaux qui forment une transition entre -1 et 1 dans un petit voisinage de l'origine. Cependant, il n'y a pas de fonction qui rend W = 0. La controverse résultant sur la validité du principe de Dirichlet est expliqué dans http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Riemann.html. Finalement, il a été montré que le principe de Dirichlet est valable, mais il nécessite une application sophistiquée de la théorie de régularité pour équations aux dérivées partielles elliptiques; voir Jost et Li-Jost (1998).
W peut être fait en choisissant arbitrairement petit fonctions linéaires par morceaux qui forment une transition entre -1 et 1 dans un petit voisinage de l'origine. Cependant, il n'y a pas de fonction qui rend W = 0. La controverse résultant sur la validité du principe de Dirichlet est expliqué dans http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Riemann.html. Finalement, il a été montré que le principe de Dirichlet est valable, mais il nécessite une application sophistiquée de la théorie de régularité pour équations aux dérivées partielles elliptiques; voir Jost et Li-Jost (1998).
Généralisation à d'autres problèmes de valeur limite
Une expression plus générale de l'énergie potentielle d'une membrane est
Ceci correspond à une densité de force externe 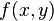 en D, une force extérieure
en D, une force extérieure 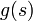 sur la frontière C, et les forces élastiques avec module
sur la frontière C, et les forces élastiques avec module 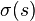 agissant sur C. La fonction qui minimise l'énergie potentielle sans restriction sur ses valeurs limites sera notée u. À condition que f et g sont continues, la théorie de la régularité implique que la fonction de minimisation u aura deux dérivés. En prenant la première variation, aucune condition à la limite doit être imposée à l'incrément v. La première variante de
agissant sur C. La fonction qui minimise l'énergie potentielle sans restriction sur ses valeurs limites sera notée u. À condition que f et g sont continues, la théorie de la régularité implique que la fonction de minimisation u aura deux dérivés. En prenant la première variation, aucune condition à la limite doit être imposée à l'incrément v. La première variante de ![V [u + \ epsilon v]](../../images/762/76225.png) est donnée par
est donnée par
Si nous appliquons le théorème de la divergence, le résultat est
Si nous fixons premier v = 0 sur C, l'intégrale de frontière disparaît, et nous concluons que avant cette
dans D. Ensuite, si nous permettons à assumer v valeurs limites arbitraires, ce qui implique que u doit satisfaire à la condition limite
sur C. Notez que cette condition limite est une conséquence de l'établissement de minimiser u: il ne est pas imposé à l'avance. Ces conditions sont appelées conditions aux limites naturelles.
Le raisonnement précédent ne est pas valide si 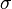 disparaît identique sur C. Dans un tel cas, on pourrait permettre une fonction d'essai
disparaît identique sur C. Dans un tel cas, on pourrait permettre une fonction d'essai 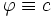 , Où c est une constante. Pour une telle fonction de procès,
, Où c est une constante. Pour une telle fonction de procès,
Par un choix approprié de c, V peut prendre toute valeur si la quantité à l'intérieur des parenthèses disparaît. Par conséquent, le problème variationnel n'a de sens que
Cette condition implique que les forces extérieurs nets du système sont en équilibre. Si ces forces sont en équilibre, alors le problème variationnel a une solution, mais elle ne est pas unique, étant donné une constante arbitraire peut être ajouté. Plus de détails et d'exemples dans Courant et Hilbert (1953).
Problèmes de valeurs propres
Les deux problèmes de valeurs propres dimensions et une multidimensionnelles peuvent être formulées sous forme de problèmes de variations.
Sturm-Liouville problèmes
Le problème aux valeurs propres Sturm-Liouville implique une forme quadratique générale
où φ est limitée à des fonctions qui satisfont aux conditions aux limites
Soit R une normalisation intégrale
Les fonctions 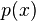 et
et 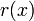 sont nécessaires pour être partout positive et délimité éloignant de zéro. Le problème variationnel primaire est de minimiser le rapport Q / R φ entre tous satisfaisant aux conditions extrémité. Il est indiqué ci-dessous que l'équation d'Euler-Lagrange pour la minimisation est u
sont nécessaires pour être partout positive et délimité éloignant de zéro. Le problème variationnel primaire est de minimiser le rapport Q / R φ entre tous satisfaisant aux conditions extrémité. Il est indiqué ci-dessous que l'équation d'Euler-Lagrange pour la minimisation est u
où λ est le quotient
On peut montrer (voir Gelfand et Fomin 1963) que le minimiser u a l'équation d'Euler-Lagrange deux dérivés et satisfait. Le λ associée sera notée 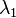 ; ce est la plus petite valeur propre de cette équation et conditions aux limites. La fonction de minimisation associé sera notée
; ce est la plus petite valeur propre de cette équation et conditions aux limites. La fonction de minimisation associé sera notée 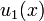 . Cette caractérisation variationnelle de valeurs propres conduit à la Méthode de Rayleigh-Ritz: Choisissez une approximation u comme une combinaison linéaire de fonctions de base (par exemple les fonctions trigonométriques) et réaliser une réduction de dimension finie parmi ces combinaisons linéaires. Cette méthode est souvent étonnamment précis.
. Cette caractérisation variationnelle de valeurs propres conduit à la Méthode de Rayleigh-Ritz: Choisissez une approximation u comme une combinaison linéaire de fonctions de base (par exemple les fonctions trigonométriques) et réaliser une réduction de dimension finie parmi ces combinaisons linéaires. Cette méthode est souvent étonnamment précis.
La prochaine plus petite valeur propre fonction propre et peuvent être obtenus en minimisant Q sous la contrainte supplémentaire
Cette procédure peut être étendue pour obtenir la séquence complète des valeurs propres et des fonctions propres au problème.
Le problème variationnel se applique également aux conditions aux limites plus générales. Au lieu d'exiger que φ disparaissent aux extrémités, nous ne pouvons pas imposer des conditions aux extrémités, et réglez
où 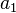 et
et 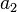 sont arbitraires. Si nous fixons
sont arbitraires. Si nous fixons 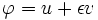 la première variation du rapport
la première variation du rapport 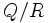 est
est
où λ est donnée par le rapport ![Q [u] / R [u]](../../images/762/76259.png) comme précédemment. Après intégration par parties,
comme précédemment. Après intégration par parties,
Si nous avons besoin d'abord que v disparaissent aux extrémités, la première variation va disparaître pour tous tels que si v
Si u satisfait cette condition, alors la première variation disparaîtra pour v arbitraire que si
Ces dernières conditions sont les conditions aux limites naturelles de ce problème, car ils ne sont pas imposés sur les fonctions d'essai pour la minimisation, mais sont plutôt une conséquence de la minimisation.
Problèmes de valeurs propres à plusieurs dimensions
Problèmes de valeurs propres dans des dimensions supérieures sont définis par analogie avec le cas unidimensionnel. Par exemple, étant donné un domaine D avec la limite B en trois dimensions nous pouvons définir
et
Soit u la fonction qui minimise le quotient ![Q [\ varphi] / R [\ varphi],](../../images/762/76265.png) sans condition prescrite à la limite B. L'équation d'Euler-Lagrange satisfaite par u est
sans condition prescrite à la limite B. L'équation d'Euler-Lagrange satisfaite par u est
où
La minimisation u doit également satisfaire à la condition de frontière naturelle
B sur la limite. Ce résultat dépend de la théorie de régularité pour des équations aux dérivées partielles elliptiques; voir Jost et Li-Jost (1998) pour plus de détails. De nombreuses extensions, y compris les résultats de complétude, propriétés asymptotiques des valeurs propres et les résultats concernant les nœuds des fonctions propres sont en Courant et Hilbert (1953).
Applications
Certaines applications du calcul des variations comprennent:
- La dérivation de la Forme caténaire
- Le problème de brachistochrone
- Problèmes isopérimétriques
- Géodésiques sur les surfaces
- Les surfaces minimales et Problème de Plateau
- Contrôle optimal
Le principe de Fermat
Principe stipule de Fermat que la lumière met un chemin qui (localement) minimise la longueur optique entre ses extrémités. Si le -Coordonner x est choisi en tant que paramètre le long du trajet, et 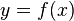 le long du chemin, la longueur optique est donnée par
le long du chemin, la longueur optique est donnée par
où l'indice de réfraction 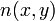 dépend du matériau. Si nous essayons
dépend du matériau. Si nous essayons 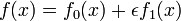 puis le première variation de A (dérivé de A par rapport à ε) est
puis le première variation de A (dérivé de A par rapport à ε) est
Après intégration par parties du premier terme entre parenthèses, on obtient l'équation d'Euler-Lagrange
Les rayons lumineux peuvent être déterminés par l'intégration de cette équation.
La loi de Snell
Il ya une discontinuité de l'indice de réfraction lorsque la lumière pénètre ou quitte une lentille. Laisser
où 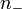 et
et 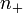 sont des constantes. Alors l'équation d'Euler-Lagrange détient comme avant dans la région où x <0 ou x> 0, et en fait le chemin est une ligne droite là, puisque l'indice de réfraction est constant. Au x = 0, f doit être continue, mais f 'peut être discontinu. Après intégration par parties dans les régions séparées et en utilisant les équations d'Euler-Lagrange, la première variation prend la forme
sont des constantes. Alors l'équation d'Euler-Lagrange détient comme avant dans la région où x <0 ou x> 0, et en fait le chemin est une ligne droite là, puisque l'indice de réfraction est constant. Au x = 0, f doit être continue, mais f 'peut être discontinu. Après intégration par parties dans les régions séparées et en utilisant les équations d'Euler-Lagrange, la première variation prend la forme
Le facteur de multiplication 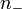 est le sinus de l'angle du rayon incident avec l'axe x, et le facteur de multiplication
est le sinus de l'angle du rayon incident avec l'axe x, et le facteur de multiplication 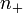 est le sinus de l'angle du rayon réfracté à l'axe x. La loi de Snell pour la réfraction exige que ces conditions soient égales. Comme le montre ce calcul, la loi de Snell est équivalente à la disparition de la première variation de la longueur du trajet optique.
est le sinus de l'angle du rayon réfracté à l'axe x. La loi de Snell pour la réfraction exige que ces conditions soient égales. Comme le montre ce calcul, la loi de Snell est équivalente à la disparition de la première variation de la longueur du trajet optique.
Le principe de Fermat en trois dimensions
Il est opportun d'utiliser la notation vectorielle: let 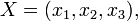 Soit t un paramètre, nous
Soit t un paramètre, nous 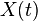 la représentation paramétrique d'une courbe C, et laisser
la représentation paramétrique d'une courbe C, et laisser 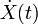 être son vecteur tangent. La longueur optique de la courbe est donnée par
être son vecteur tangent. La longueur optique de la courbe est donnée par
Notez que cette intégrale est invariante par rapport aux changements dans la représentation paramétrique de C. Les équations d'Euler-Lagrange pour une courbe minimisant ont la forme symétrique
où
Il résulte de la définition qui satisfait P
Par conséquent l'intégrale peut aussi se écrire
Ce formulaire suggère que si nous pouvons trouver une fonction ψ dont la pente est donnée par P, puis l'A intégrale est donnée par la différence de ψ aux extrémités de l'intervalle d'intégration. Ainsi, le problème de l'étude des courbes qui font partie intégrante de la stationnaire peut être liée à l'étude des surfaces planes de ψ. Afin de trouver une telle fonction, nous nous tournons vers l'équation d'onde, qui régit la propagation de la lumière.
Connexion avec l'équation d'onde
Le équation d'onde pour un milieu inhomogène est
où c est la vitesse, qui dépend généralement de X. Fronts d'onde pour la lumière sont des surfaces caractéristiques de cette équation aux dérivées partielles: ils satisfont
Nous pouvons chercher des solutions dans la forme
Dans ce cas, satisfait ψ
où 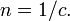 Selon la théorie de équations aux dérivées partielles du premier ordre, si
Selon la théorie de équations aux dérivées partielles du premier ordre, si 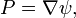 alors p satisfait
alors p satisfait
le long d'un système de courbes (les rayons de lumière) qui sont donnés par
Ces équations pour la solution d'une équation aux dérivées partielles du premier ordre sont identiques aux équations d'Euler-Lagrange si nous faisons l'identification
Nous concluons que la fonction ψ est la valeur de la minimisation d'une intégrale en fonction du point d'extrémité supérieur. Autrement dit, quand une famille de courbes est construite et réduit, les valeurs de la longueur optique satisfont l'équation caractéristique de l'équation d'onde correspondant. Par conséquent, la résolution de l'équation différentielle partielle associé de premier ordre est équivalent à trouver des familles de solutions du problème variationnel. Ce est le contenu essentiel de la La théorie de Hamilton-Jacobi, qui se applique à plus de problèmes variationnels générales.
Le principe d'action
L'action a été définie par Hamilton pour l'intégrale de temps du lagrangien, L, qui est défini comme la différence des énergies:
où T est l'énergie cinétique d'un système mécanique et U est l'énergie potentielle. Le principe de Hamilton (ou le principe d'action) stipule que le mouvement d'un conservatrices holonomes (contraintes intégrables) système mécanique est telle que l'action intégrale
est fixe par rapport aux variations du chemin x (t). Les équations d'Euler-Lagrange pour ce système sont connus comme les équations de Lagrange:
et ils sont équivalentes aux équations de Newton sur le mouvement (pour ces systèmes).
Le conjugué impulsions P sont définis par
Par exemple, si
puis
Mécanique hamiltonienne résultats si l'moments conjugués sont introduits à la place de 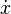 Et le lagrangien L est remplacé par le hamiltonien H défini par
Et le lagrangien L est remplacé par le hamiltonien H défini par
Le hamiltonien est l'énergie totale du système: H = T + U. Analogie avec le principe de Fermat suggère que les solutions des équations de Lagrange (les trajectoires des particules) peuvent être décrits en termes de surfaces de niveau d'une fonction de X. Cette fonction est une solution de la Équation de Hamilton-Jacobi:


![A [f] = \ {int_ x_1} ^ {} x_2 L (x, f, f ') \, dx. \,](../../images/761/76191.png)
![A [f_0] \ le A [f_0 + \ epsilon \ eta]](../../images/761/76196.png)
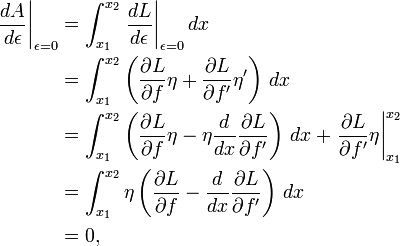
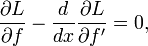
![A [f] = \ {int_ x_1} ^ {x_2} \ sqrt {1 + [f '(x)] ^ 2} \, dx,](../../images/762/76203.png)
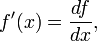
![\ {Int_ x_1} ^ {} x_2 \ frac {f_0 '(x) \ eta' (x)} {\ sqrt {1 + [f_0 '(x)] ^ 2}} \, dx = 0, \,](../../images/762/76208.png)
![\ Int_a ^ bu (x) \ eta '(x) \, dx = \ left [u (x) \ eta (x) \ right] _ {a} ^ {b} - \ int_a ^ b u' (x) \ eta (x) \, dx](../../images/762/76210.png)
![u (x) = \ frac {f_0 '(x)} {\ sqrt {1 + [f_0' (x)] ^ 2}}](../../images/762/76211.png)
![\ Left [u (x) \ eta (x) \ right] _ {} ^ {x_1 x_2} - \ {int_ x_1} ^ {} x_2 \ eta (x) \ frac {d} {dx} \ left [\ frac {f_0 '(x)} {\ sqrt {1 + [f_0' (x)] ^ 2}} \ right] \, dx = 0,](../../images/762/76212.png)
![\ {Int_ x_1} ^ {} x_2 \ eta (x) \ frac {d} {dx} \ left [\ frac {f_0 '(x)} {\ sqrt {1 + [f_0' (x)] ^ 2} } \ right] \, dx = 0](../../images/762/76214.png)
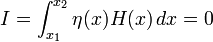
![\ Frac {d} {dx} \ left [\ frac {f_0 '(x)} {\ sqrt {1 + [f_0' (x)] ^ 2}} \ right] = 0. \,](../../images/762/76217.png)
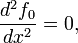
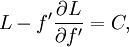
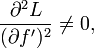
![U [\ varphi] = \ iint_D \ sqrt {1 + \ nabla \ varphi \ cdot \ nabla \ varphi} dx \, dy. \,](../../images/762/76222.png)
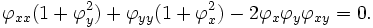
![V [\ varphi] = \ frac {1} {2} \ iint_D \ nabla \ varphi \ cdot \ nabla \ varphi \, dx \, dy. \,](../../images/762/76224.png)
![\ Frac {d} {d \ epsilon} V [u + \ epsilon v] | _ {\ epsilon = 0} = \ iint_D \ nabla u \ cdot \ nabla v \, dx \, dy = 0. \,](../../images/762/76226.png)
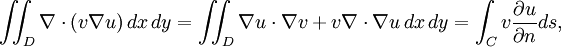
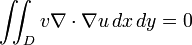
![W [\ varphi] = \ int _ {- 1} ^ {1} (x \ varphi ') ^ 2 \, dx \,](../../images/762/76231.png)
![V [\ varphi] = \ iint_D \ left [\ frac {1} {2} \ nabla \ varphi \ cdot \ nabla \ varphi + f (x, y) \ varphi \ right] \, dx \, dy \, + \ int_C \ left [\ frac {1} {2} \ sigma (s) \ varphi ^ 2 + g (s) \ varphi \ right] \, ds.](../../images/762/76234.png)
![\ Iint_D \ left [\ nabla u \ cdot \ nabla v + fv \ right] \, dx \, dy + \ int_C \ left [\ sigma uv + gv \ right] \, ds = 0. \,](../../images/762/76238.png)
![\ Iint_D \ left [-v \ nabla \ cdot \ nabla u + vf \ right] \, dx \, dy + \ int_C v \ left [\ frac {\ part u} {\ part n} + \ sigma u + g \ right] \, ds = 0. \,](../../images/762/76239.png)
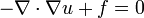
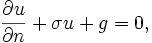
![V [c] = c \ gauche [\ iint_D f \, dx \, dy + \ int_C g ds \ right].](../../images/762/76243.png)
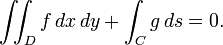
![Q [\ varphi] = \ {int_ x_1} ^ {} x_2 \ left [p (x) \ varphi '(x) ^ 2 + q (x) \ varphi (x) ^ 2 \ right] \, dx, \ ,](../../images/762/76245.png)

![R [\ varphi] = \ {int_ x_1} ^ {} x_2 r (x) \ varphi (x) ^ 2 \, dx \.,](../../images/762/76247.png)
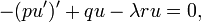
![\ Lambda = \ frac {Q [u]} {R [u]}. \,](../../images/762/76251.png)
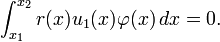
![Q [\ varphi] = \ {int_ x_1} ^ {} x_2 \ left [p (x) \ varphi '(x) ^ 2 + q (x) \ varphi (x) ^ 2 \ right] \, dx + a_1 \ varphi (x_1) ^ 2 + a_2 \ varphi (x_2) ^ 2, \,](../../images/762/76255.png)
![V_1 = \ frac {2} {R [u]} \ left (\ {int_ x_1} ^ {} x_2 \ left [p (x) u '(x) v' (x) + q (x) u (x ) v (x) - \ lambda u (x) v (x) \ right] \, dx + a_1 u (x_1) v (x 1) + a_2 u (x_2) v (x_2) \ right), \,](../../images/762/76258.png)
![\ Frac {R [u]} {2} V_1 = \ {int_ x_1} ^ {} x_2 v (x) \ left [- (p u ')' + qu - \ lambda ru \ right] \, dx + v (x_1) [-p (x_1) u '(x 1) + a_1 u (x_1)] + v (x_2) [p (x_2 u' (x_2) + a_2 u (x_2). \,](../../images/762/76260.png)
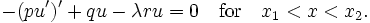
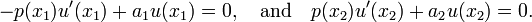
![Q [\ varphi] = \ iiint_D p (X) \ nabla \ varphi \ cdot \ nabla \ varphi + q (X) \ varphi ^ 2 \, dx \, dy \, dz + \ iint_B \ sigma (S) \ varphi ^ 2 \, dS, \,](../../images/762/76263.png)
![R [\ varphi] = \ iiint_D r (X) \ varphi (X) ^ 2 \, dx \, dy \, dz. \,](../../images/762/76264.png)
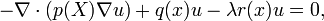
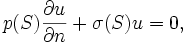
![A [f] = \ int_ {x = x 0} ^ {} x_1 n (x, f (x)) \ sqrt {1 + f '(x) ^ 2} dx, \,](../../images/762/76268.png)
![\ Delta A [f_0, f_1] = \ int_ {x = x 0} ^ {} x_1 \ left [\ frac {n (x, f_0) f_0 '(x) f_1' (x)} {\ sqrt {1 + f_0 '(x) ^ 2}} + n_y (x, f_0) f_1 \ sqrt {1 + f_0' (x) ^ 2} \ right] dx.](../../images/762/76271.png)
![- \ Frac {d} {dx} \ left [\ frac {n (x, f_0) f_0 '} {\ sqrt {1 + f_0' ^ 2}} \ right] + n_y (x, f_0) \ sqrt {1 + f_0 '(x) ^ 2} = 0. \,](../../images/762/76272.png)
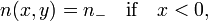
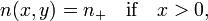
![\ Delta A [f_0, f_1] = f_1 (0) \ left [n _- \ frac {f_0 '(0 _-)} {\ sqrt {1 + f_0' (0 _-) ^ 2}} -n _ + \ frac { f_0 '(0 + _)} {\ sqrt {1 + f_0' (0 + _) ^ 2}} \ right]. \,](../../images/762/76277.png)
![A [C] = \ int_ {t = t_0} ^ {} t_1 n (X) \ sqrt {\ dot X \ cdot \ dot X} dt. \,](../../images/762/76281.png)
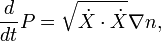
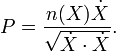
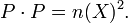
![A [C] = \ int_ {t = t_0} ^ {} t_1 P \ cdot \ dot X \, dt \.,](../../images/762/76285.png)
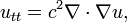
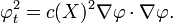
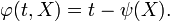
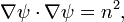
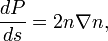
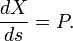
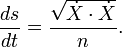
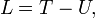
![A [C] = \ int_ {t = t_0} ^ {} t_1 L (x, \ point x, t) dt \,](../../images/762/76296.png)