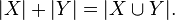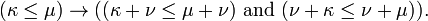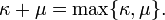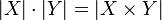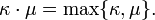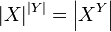Nombre cardinal

Aleph-0, le plus petit cardinal infini

En mathématiques , les nombres cardinaux, cardinaux ou pour faire court, sont une sorte généralisé de nombre utilisé pour désigner la taille d'un définir, connu sous le nom de son cardinalité. Pour ensembles finis le cardinal est donnée par un nombre naturel , étant simplement le nombre d'éléments dans l'ensemble. Il y a aussi nombres cardinaux transfinis pour décrire la taille des ensembles infinis. D'une part, un sous-ensemble A d'une ensemble infini S peut avoir le même cardinal S. D'autre part, peut-être aussi contre-intuitivement, tous les ensembles infinis ont la même cardinalité. Il est une caractérisation formelle qui explique comment certains ensembles infinis ont cardinalités qui sont strictement inférieure à d'autres ensembles infinis.

Les nombres cardinaux sont: 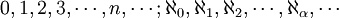. Autrement dit, ce sont des nombres naturels (les cardinaux finis), suivie par la aleph (numéros de cardinaux infinis). Les numéros de aleph sont indexés par les nombres ordinaux . Les nombres naturels et les numéros de aleph sont sous-classes des nombres ordinaux. Si le axiome du choix échoue, la situation devient plus compliquée - il ya cardinaux infinis supplémentaires qui ne sont pas alephs.

Concepts de cardinalité sont intégrés dans la plupart des branches des mathématiques et sont essentiels à leur étude. Cardinalité est aussi une zone étudiée pour elle-même dans le cadre de la théorie des ensembles , notamment en essayant de décrire les propriétés de grands cardinaux.

Histoire

La notion de cardinal, comme maintenant compris, a été formulée par Georg Cantor , à l'origine de la théorie des ensembles , en 1874-1884.

Cantor abord établi cardinal comme un instrument de comparer des ensembles finis; par exemple, les ensembles {1,2,3} et {2,3,4} ne sont pas égaux, mais ont la même cardinalité, à savoir trois.

Cantor a identifié le fait que one-to-one correspondance est la façon de dire que deux ensembles ont la même taille, appelé "cardinal", dans le cas d'ensembles finis. En utilisant cette correspondance un-à-un, il a appliqué le concept d'ensembles infinis; par exemple, l'ensemble des nombres naturels N = {0, 1, 2, 3, ...}. Il a appelé ces nombres cardinaux nombres cardinaux transfinis, et définis tous les jeux ayant un one-to-one correspondance avec N d'être dénombrables (dénombrable) ensembles.

Nommer ce numéro de cardinal 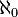, aleph-nulle, Cantor prouvé que tout sous-ensemble sans limite de N a le même cardinal que le N, même si cela peut sembler à première vue contraire à l'intuition. Il se est avéré également que l'ensemble de tous paires ordonnées de nombres naturels est dénombrable (ce qui implique que l'ensemble des nombres rationnels est dénombrable), et plus tard ont prouvé que l'ensemble de tous nombres algébriques est aussi dénombrable. Chaque nombre algébrique z peut être codé comme une suite finie de nombres entiers qui sont les coefficients de l'équation polynomiale de laquelle ce est la solution, à savoir le n-tuple ordonné 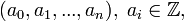avec une paire de nombres rationnels 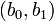de telle sorte que z est la racine unique du polynôme avec des coefficients 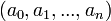qui se situe dans l'intervalle .

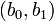Dans son article de 1874, Cantor a prouvé qu'il existe des nombres cardinaux d'ordre supérieur en montrant que l'ensemble des nombres réels est de cardinal supérieur à celui de N. Son présentation originale utilisé un argument complexe avec intervalles imbriqué, mais dans un document de 1891, il se est avéré le même résultat en utilisant son ingénieuse, mais simple argument de la diagonale. Ce nouveau numéro de cardinal, appelé cardinalité du continuum, a été appelé par Cantor c.

Cantor a également développé une grande partie de la théorie générale des nombres cardinaux; il a prouvé qu'il ya un plus petit nombre cardinal transfini ( 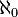, Aleph-nulle) et que pour chaque nombre cardinal, il est un cardinal de la prochaine grande .

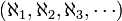Son continuum hypothèse est la proposition selon laquelle c est la même que 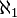, Mais cela a été jugée indépendante des axiomes standard de la théorie mathématique des ensembles; il ne peut être ni prouvée ni réfutée selon les hypothèses standard.

Motivation

Lors de l'utilisation informelle, un nombre cardinal est ce qui est normalement appelé un numéro de comptage , à condition que 0 est inclus: 0, 1, 2, .... Ils peuvent être identifiés par les nombres naturels à partir de 0. Les numéros de comptage sont exactement ce qui peut être défini officiellement comme le nombres cardinaux finis. Cardinaux infinis se produisent seulement en mathématiques de niveau supérieur et de la logique.

Plus formellement, un nombre différent de zéro peut être utilisé à deux fins: pour décrire la taille d'un ensemble, ou pour décrire la position d'un élément dans une séquence. Pour les jeux et suites finies, il est facile de voir que ces deux notions coïncident, puisque pour chaque numéro décrivant une position dans une séquence nous pouvons construire un ensemble qui a exactement la bonne taille, par exemple 3 décrit la position de «c» dans la séquence <'a', 'b', 'c', 'd', ...>, et nous pouvons construire l'ensemble {a, b, c} qui a trois éléments. Cependant lorsqu'il se agit de ensembles infinis, il est essentiel de faire la distinction entre les deux - les deux notions sont en fait différent pour les ensembles infinis. Compte tenu de l'aspect de position conduit à des nombres ordinaux, tandis que l'aspect de la taille est généralisée par les nombres cardinaux décrites ici.

L'intuition de la définition formelle de cardinal est la construction d'une notion de la taille relative ou «grandeur» d'un ensemble sans référence au genre de membres dont il dispose. Pour ensembles finis ce est facile; on compte simplement le nombre d'éléments d'un ensemble a. Afin de comparer les tailles de plus grands ensembles, il est nécessaire de faire appel à des notions plus subtiles.

Un ensemble Y est au moins aussi grand que, ou égal ou supérieur à un ensemble X se il existe une injective (one-to-one) la cartographie des éléments de X à Y éléments de. Une cartographie one-to-one identifie chaque élément de l'ensemble X avec un élément unique de l'ensemble Y. Ce est plus facile à comprendre par un exemple; supposons que nous avons les ensembles X = {1,2,3} et Y = {a, b, c, d}, puis en utilisant cette notion de taille, nous ne observer qu'il existe une cartographie:

1 → a

2 → b

→ 3 c

qui est l'un-à-un, et donc conclure que Y est de cardinal supérieur ou égal à X. Remarque l'élément d a aucun élément à la cartographie, mais cela est permis car nous ne avons besoin d'un mappage un-à-un, et pas nécessairement un one-to-one et sur la cartographie. L'avantage de cette notion est que cela peut être étendu à des ensembles infinis.

Nous pouvons ensuite l'étendre à une relation d'égalité de style. Deux ensembles sont dit X et Y pour avoir le même cardinal se il existe une bijection entre X et Y. Par le Schroeder-Bernstein théorème, ce est l'équivalent d'y être à la fois un mappage un-à-un de X à Y et un mappage un-à-un de Y à X. Nous écrivons alors | X | = | Y |. Le cardinal de X lui-même est souvent définie comme le moins un ordinal avec | a | = | X |. Ceci est appelé le von Neumann Affectation cardinal; cette définition à donner un sens, il doit être prouvé que chaque ensemble a le même cardinal que certains ordinale; cette déclaration est le principe bien commander. Il est cependant possible de discuter de la cardinalité relative des ensembles sans attribuer explicitement les noms aux objets.

L'exemple classique utilisée est celle de l'hôtel infinie paradoxe, également appelée Hôtel de Hilbert. Supposons que vous êtes un aubergiste dans un hôtel avec un nombre infini de chambres. L'hôtel est plein, puis un nouveau client arrive. Il est possible de se adapter à la personne supplémentaire en demandant à l'invité qui était dans la chambre 1 pour passer à la salle 2, l'invité dans la salle 2 de se déplacer à la salle 3, et ainsi de suite, laissant la place une vacants. Nous pouvons écrire explicitement un segment de cette cartographie:

1 ↔ 2

2 ↔ 3

3 ↔ 4

...

n ↔ n + 1

...

De cette façon, nous pouvons voir que l'ensemble {1,2,3, ...} a le même cardinal que l'ensemble {2,3,4, ...} depuis une bijection entre le premier et le second a été montré . Ce qui motive la définition d'un ensemble infini étant tout ensemble qui a un sous-ensemble de la même cardinal; dans ce cas, {2,3,4, ...} est un sous-ensemble de {1,2,3, ...}.

Lors de l'examen de ces grands objets, nous pourrions également voir si la notion d'ordre de comptage coïncide avec celle du cardinal défini ci-dessus pour ces ensembles infinis. Il se trouve que ce ne est pas; en considérant l'exemple ci-dessus, nous pouvons voir que si un objet "de plus grand que l'infini" existe, alors il doit avoir le même cardinal que l'ensemble infini nous avons commencé avec. Il est possible d'utiliser une notion formelle différente pour le nombre, appelé ordinaux, basée sur les idées de compter et compte tenu de chaque numéro à son tour, et nous découvrons que les notions de cardinal et ordinal sont divergents une fois que nous sortons des nombres finis.

Il peut être prouvé que la cardinalité des nombres réels est supérieure à celle des nombres naturels viennent d'être décrits. Ceci peut être visualisé en utilisant Argument de la diagonale de Cantor; questions classiques de cardinal (par exemple la continuum hypothèse) sont concernés par découvrir si il ya une certaine cardinal entre certains autres paire de cardinaux infinis. Dans une époque plus récente mathématiciens ont décrit les propriétés des cardinaux plus en plus grandes.

Depuis cardinal est un tel concept commun en mathématiques, une variété de noms sont en cours d'utilisation. Similitude de cardinal est parfois appelé équipotence, équipollence ou Équipotence. Il est donc dit que deux ensembles avec le même cardinal sont, respectivement, équipotente isosthénique ou equinumerous.

Définition formelle

Formellement, en supposant que le axiome de choix, la cardinalité d'un ensemble X α est le moins ordinal tel qu'il existe une bijection entre X et α. Cette définition est connue comme la von Neumann Affectation de cardinal. Si l'axiome du choix ne est pas supposé que nous devons faire quelque chose de différent. La définition la plus ancienne de la cardinalité d'un ensemble X (implicite dans Cantor et explicite dans Frege et Principia Mathematica) est comme l'ensemble de tous les ensembles qui sont equinumerous avec X: cela ne fonctionne pas dans ZFC ou d'autres systèmes connexes de la théorie des ensembles axiomatique parce que cette collection est trop grand pour être un ensemble, mais il ne fonctionne dans tapez théorie et en Nouvelles fondations et des systèmes connexes. Toutefois, si nous limitons de cette classe à ces equinumerous avec X qui ont le moins rang, alors il fonctionne (ce est un truc en raison de Dana Scott: cela fonctionne parce que la collection d'objets avec ne importe quel rang donné est un ensemble).

Formellement, l'ordre entre les nombres cardinaux est défini comme suit: | X | ≤ | Y | signifie qu'il existe un fonction injective de X à Y. Le Théorème de Cantor-Bernstein indique que si | X | ≤ | Y | et | Y | ≤ | X | puis | X | = | Y |. Le axiome du choix est équivalente à l'instruction que, étant donné deux ensembles X et Y, soit | X | ≤ | Y | ou | Y | ≤ | X |.

Un ensemble X est Dedekind-infini se il existe un sous-ensemble approprié de X avec Y | X | = | Y |, et Dedekind-finis se il ne existe pas un tel sous-ensemble. Le cardinaux finis sont seulement les nombres naturels , ce est à dire, un ensemble X est fini si et seulement si | X | = | n | = n pour un nombre naturel n. Toute autre ensemble est infinie. En supposant que l'axiome du choix, il peut être prouvé que les notions de Dedekind correspondent aux standards. Il peut également être prouvé que le cardinal 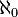(Aleph-0, où aleph est la première lettre dans le Alphabet hébreu, représentée 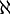) De l'ensemble des nombres naturels est le plus petit cardinal infini, ce est à dire que tout ensemble infini a un sous-ensemble de cardinal 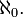Le prochain grand cardinal est désigné par 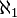et ainsi de suite. Pour chaque ordinal α il ya un nombre cardinal 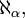et cette liste épuise tous les numéros de cardinal infini.

Cardinal arithmétique

Nous pouvons définir arithmétiques opérations sur les nombres cardinaux qui généralisent les opérations ordinaires pour les nombres naturels. Il peut être démontré que, pour les cardinaux finis ces opérations coïncident avec les opérations habituelles de nombres naturels. En outre, ces opérations part de nombreuses propriétés avec l'arithmétique ordinaire.

Successeur cardinal

Si l'axiome du choix tient, chaque cardinal κ a un successeur κ ^+> κ, et il n'y a pas entre cardinaux κ et son successeur. Pour cardinaux finis, le successeur est tout simplement κ + 1. Pour cardinaux infinis, le cardinal successeur diffère de la successeur ordinale.

Cardinal plus

Si X et Y sont disjoints, l'addition est donnée par la union de X et Y. Si les deux ensembles ne sont pas déjà disjoints, ils peuvent être remplacés par des ensembles disjoints, ce est à dire remplacer X par X × {0} et Y par Y × {1}.

Zéro est une identité additif κ + 0 = 0 + κ = κ.

L'addition est associative (κ + μ) + ν = κ + (μ + ν).

L'addition est commutative κ + μ = μ + κ.

L'addition est non décroissante dans les deux arguments:

Si l'axiome du choix détient, outre des numéros de cardinal infini est facile. Si l'une 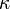ou 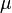est infini, alors

Soustraction

Si l'axiome du choix détient et donné un σ de cardinal infini et un μ cardinal, il y aura un cardinal κ telle que μ + κ = σ si et seulement si μ ≤ σ. Il sera unique (et égal à σ) si et seulement si μ <σ.

Cardinal multiplication

Le produit des cardinaux vient du produit cartésien.

κ · 0 = 0 · κ = 0.

κ · μ = 0 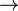(Κ = 0 ou μ = 0).

L'un est un κ identité multiplicatif · 1 = 1 · κ = κ.

La multiplication est associative (κ · μ) · ν = κ · (μ · ν).

La multiplication est commutative κ · μ = μ · κ.

La multiplication est non décroissante dans les deux arguments: κ ≤ μ (Κ · ν ≤ μ ν et ν · · · κ ≤ ν μ).

Multiplication distribue sur l'addition: κ · (μ + ν) = κ · μ + κ · ν et (μ + ν) · κ = μ · κ + ν · κ.

Si l'axiome du choix détient, multiplication des nombres cardinaux infinis est également facile. Si l'une ou κ μ est infinie et les deux sont non-zéro,

Division

Si l'axiome du choix détient et donné un π cardinal infini et un cardinal μ non nul, il y aura un cardinal κ telle que μ · κ = π si et seulement si μ ≤ π. Il sera unique (et égale à π) si et seulement si μ <π.

Cardinal exponentiation

Exponentiation est donnée par

^Y où X est l'ensemble de toutes les fonctions de Y à X.

κ ⁰ = 1 (en particulier ⁰ 0 = 1), voir fonction vide.

Si une ≤ μ, puis 0 ^μ = 0.

1 ^μ = 1.

κ = κ ^1.

^κ μ ^{+ ν} = ^κ μ · κ ^ν.

^κ μ ^{· ν} = ^(κ μ) ^ν.

(Κ · μ) ^ν = κ ^ν · μ ^ν.

Si κ et μ sont à la fois fini et supérieur à 1, et ν est infini, alors κ ^ν = μ ^ν.

Si κ est infini et μ est finie et non nulle, alors κ = κ ^μ.

Exponentiation est non décroissante dans les deux arguments:

(1 ≤ μ ν et κ ≤) 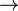^(Ν κ ≤ ν μ) et

(Κ ≤ μ) 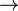^(Κ ν ≤ μ ν).

Notez que 2 ^{| X |} est la cardinalité de la ensemble de l'ensemble X de puissance et Argument de la diagonale de Cantor montre que 2 ^{| X |>} | X | X pour tout ensemble. Cela prouve que pas grand cardinal existe (car pour tout κ cardinaux, nous pouvons toujours trouver un plus grand cardinal ^κ 2). En fait, la classe de cardinaux est un classe appropriée.

Si l'axiome du choix et détient 2 ≤ κ et une ≤ μ et au moins un d'entre eux est infini, alors:

Max (κ, ^μ 2) ≤ κ ^μ ≤ max (2 ^{κ, μ} 2).

Utilisation Théorème de König, peut prouver κ <κ ^{cf (κ)} et κ <cf (2 ^κ) pour toute κ cardinaux infinis, où cf (κ) est le cofinalité de κ.

Sans racines ni logarithmes peuvent être définis uniquement pour cardinaux infinis.

Le logarithme d'un nombre cardinal infini κ est défini comme étant le nombre minimum de cardinal μ tel que κ ≤ 2 ^μ. Logarithmes des cardinaux infinis sont utiles dans certains domaines des mathématiques, par exemple dans l'étude des invariants cardinaux d'espaces topologiques, se ils ne ont pas certaines des propriétés que logarithmes des nombres réels positifs possèdent.

L'hypothèse de continuum

Le continuum hypothèse (CH) affirme qu'il n'y a pas strictement entre cardinaux 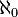et 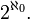Ce dernier nombre cardinal est également souvent désigné par c; c'est le cardinalité du continuum (l'ensemble des nombres réels ). Dans ce cas 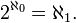Le continuum généralisée hypothèse (GCH) stipule que pour chaque ensemble infini X, il n'y a pas strictement entre cardinaux | X | et 2 ^{| X |.} L'hypothèse de continuum est indépendante des axiomes habituels de la théorie des ensembles, le Zermelo-Fraenkel axiomes avec l'axiome du choix ( ZFC).