La théorie du chaos

Une parcelle de la Lorenz attracteur pour les valeurs r = 28, σ = 10, b = 8/3

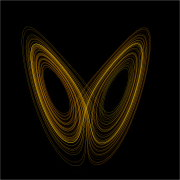
Dans les mathématiques et la physique , la théorie du chaos décrit le comportement de certains non linéaire systèmes dynamiques qui peuvent présenter dynamiques qui sont très sensibles aux conditions initiales (populairement dénommée effet papillon). En raison de cette sensibilité, qui se manifeste par une croissance exponentielle des perturbations dans les conditions initiales, le comportement de systèmes chaotiques semble aléatoire. Cela se produit même si ces systèmes sont déterministe, ce qui signifie que leur dynamique futurs sont entièrement définies par leurs conditions initiales, sans éléments aléatoires impliqués. Ce comportement est connu que le chaos déterministe, ou tout simplement chaos.

Vue d'ensemble

Comportement chaotique a été observé en laboratoire dans une variété de systèmes, y compris circuits électriques, lasers , oscillants réactions chimiques , la dynamique des fluides, et des dispositifs mécaniques et magnéto-mécaniques. Les observations du comportement chaotique dans la nature comprennent les dynamiques de satellites dans le système solaire , l'évolution temporelle de la champ magnétique des corps célestes, la croissance de la population dans l'écologie , la dynamique des potentiels d'action dans les neurones, et vibrations moléculaires. Exemples quotidiens de systèmes chaotiques comprennent la météo et le climat . Il ya une certaine controverse sur l'existence de dynamiques chaotiques dans les tectonique des plaques et de l'économie .

Les systèmes qui présentent le chaos mathématique déterministes et donc ordonnée dans un certain sens; cette utilisation technique du mot chaos est en contradiction avec le langage courant, ce qui suggère un désordre complet. Un domaine connexe de la physique appelée quantique systèmes études de théorie du chaos qui suivent les lois de la mécanique quantique . Récemment, un autre champ, appelé chaos relativiste, a émergé pour décrire les systèmes qui suivent les lois de la relativité générale .

En plus d'être ordonnée dans le sens d'être déterministe, systèmes chaotiques ont généralement bien définies statistiques . Par exemple, le Système de Lorenz photo est chaotique, mais a une structure bien définie. Chaos borné est un terme utile pour décrire les modèles de désordre.

Histoire

Fractal fougère créée à l'aide jeu chaos. Formes naturelles (fougères, nuages, montagnes, etc.) peuvent être recréées par un Système de fonctions itérées (IFS).

Le premier découvreur du chaos peut plausiblement faire valoir d'être Jacques Hadamard, qui, en 1898 a publié une étude influente du mouvement chaotique d'une particule libre glisse sans frottement sur une surface de courbure négative constante. Dans le système étudié, Les billards de Hadamard, Hadamard a pu montrer que toutes les trajectoires sont instables, en ce que toutes les trajectoires des particules divergent de façon exponentielle les uns des autres, avec un positif Exposant de Lyapunov.

Au début des années 1900 Henri Poincaré, en étudiant la problème des trois corps, trouvé qu'il peut y avoir des orbites qui sont non périodique, et pourtant pas éternellement augmenter ni l'approche d'un point fixe. Une grande partie de la théorie début a été développé presque entièrement par les mathématiciens, sous le nom de théorie ergodique. Des études ultérieures, également sur le thème des équations différentielles non linéaires, ont été réalisées par GD Birkhoff, AN Kolmogorov, ML Cartwright, JE Littlewood, et Stephen Smale. Sauf pour Smale, ces études ont toutes été directement inspirés par la physique: le problème des trois corps dans le cas de Birkhoff, la turbulence et les problèmes astronomiques dans le cas de Kolmogorov, et de l'ingénierie de la radio dans le cas de Cartwright et Littlewood. Bien que le mouvement planétaire chaotique ne avait pas été observée, les expérimentateurs ont rencontré de la turbulence dans un mouvement fluide et l'oscillation non périodique dans les circuits de radio sans le bénéfice d'une théorie pour expliquer ce qu'ils voyaient.

Malgré un premier aperçu dans la première moitié du siècle, la théorie du chaos est devenue formalisée en tant que telle qu'après le milieu du siècle, quand il se est d'abord manifestée par certains scientifiques qui théorie linéaire, la théorie du système en vigueur à l'époque, ne pouvait tout simplement pas expliquer le comportement observé de certaines expériences comme celle de la carte logistique. Ce qui avait été préalablement exclus que mesurer l'imprécision et simple " bruit »a été considéré par les théories du chaos comme une composante à part entière des systèmes étudiés.

Le catalyseur principal pour le développement de la théorie du chaos est le électronique ordinateur . Une grande partie des mathématiques de la théorie du chaos implique l'itération répétée de formules mathématiques simples, ce qui serait difficile de le faire à la main. Ordinateurs électroniques ont fait ces calculs répétés pratique, tandis que les chiffres et les images ont permis de visualiser ces systèmes. Un des premiers ordinateurs numériques électroniques, ENIAC, a été utilisé pour exécuter des modèles de prévision du temps simples.

La turbulence dans la tourbillon d'extrémité d'un aile d'avion. Les études de la point critique au-delà duquel un système crée de la turbulence était important pour la théorie du chaos, analysée par exemple par le physicien soviétique Lev Landau qui a développé le Théorie de Landau-Hopf de turbulence. David Ruelle et Floris Takens tard prédit, contre Landau, que la turbulence des fluides pourrait se développer à travers un attracteur étrange, un concept principal de la théorie du chaos.

L'un des pionniers de la théorie était Edward Lorenz dont l'intérêt dans le chaos est venu à propos accidentellement par son travail sur la prévision du temps en 1961 . Lorenz utilisait un système numérique simple ordinateur , un McBee royal LGP-30, pour exécuter son simulation météo. Il voulait voir une séquence de données à nouveau et de gagner du temps, il a commencé la simulation au milieu de son cours. Il était capable de faire cela en saisissant une impression des données correspondant à des conditions au milieu de sa simulation dont il avait calculé la dernière fois.

À sa grande surprise le temps que la machine a commencé à prévoir était complètement différente de la météo calculé avant. Lorenz suivi cette baisse à l'imprimé d'ordinateur. L'ordinateur a travaillé avec une précision de 6 chiffres, mais l'impression des variables arrondi à un nombre à 3 chiffres, donc une valeur comme 0,506127 a été imprimé comme 0,506. Cette différence est minuscule et le consensus au moment aurait été qu'il aurait eu pratiquement aucun effet. Cependant Lorenz avait découvert que de petits changements dans les conditions initiales produits de grands changements dans les résultats à long terme. La découverte de Lorenz, qui a donné son nom à Attracteurs de Lorenz, ont prouvé que la météorologie ne pouvait raisonnablement prévoir le temps au-delà d'une période hebdomadaire (au plus).

L'année d'avant, Benoit Mandelbrot trouvé modèles récurrents à toutes les échelles dans les données sur les les prix du coton. Auparavant, il avait étudié théorie de l'information et conclu le bruit a été modelé comme un Ensemble de Cantor: périodes à une échelle la proportion des périodes contenant de bruit à l'erreur-libres était un constant-- donc erreurs étaient inévitables et doivent être prévues pour en incorporant redondance. Mandelbrot décrit à la fois la Effet Noah (dans lequel les changements soudains discontinues peuvent se produire, par exemple, des prix des actions après une mauvaise nouvelles, ainsi difficile la distribution normale théorie dans les statistiques , alias courbe de Bell) et la Joseph effet (dans lequel la persistance d'une valeur peut se produire pendant un certain temps, mais soudainement changer par la suite). En 1967, il a publié Quelle est la durée de la côte de la Bretagne? Statistique d'auto-similarité et fractionnaire Dimension, montrant que la longueur d'un littoral varie avec l'échelle de l'instrument de mesure, lui-même ressemble à toutes les échelles, et est une longueur infinie pour un dispositif de mesure infiniment petit. Arguant que une boule de ficelle semble être une dimensions (de loin), trois dimensions (assez proche), ou 1 dimensions (fermer), il a soutenu que les dimensions d'un objet sont liés à l'observateur et peuvent être fractionnée. Un objet dont l'irrégularité est constante sur différentes échelles ("auto-similarité") est une fractale (par exemple, le Courbe de Koch ou " flocon de neige ", ce qui est infiniment longue encore enferme un espace à dimensions finies = 1,2618; ou le Éponge de Menger et Triangle de Sierpinski). En 1975, Mandelbrot publié La géométrie fractale de la nature, qui est devenu un classique de la théorie du chaos. Les systèmes biologiques tels que la ramification des systèmes circulatoire et bronchiques prouvé pour se adapter à un modèle fractal.

Yoshisuke Ueda identifié indépendamment un phénomène chaotique en tant que telle en utilisant un calculateur analogique le 27 Novembre, 1961. Le chaos exposé par un calculateur analogique est un phénomène réel, contrairement à ceux que les ordinateurs numériques calculent, qui a un autre type de limite sur la précision. Le professeur superviseur de Ueda, Hayashi, ne croyait pas dans le chaos, et donc il a interdit Ueda de publier ses conclusions jusqu'au 1970 .

En Décembre 1977, le Académie des sciences de New York a organisé le premier colloque sur le chaos, en présence de David Ruelle, Robert mai, James Yorke (monnayeur du terme «chaos» tel qu'il est utilisé en mathématiques), Robert Shaw (un physicien, une partie de la Groupe avec Eudaemons J. Doyne Farmer et Norman Packard qui a essayé de trouver une méthode mathématique pour battre roulette, puis créé avec eux le Systèmes dynamiques collectives dans Santa Cruz), et le météorologue Edward Lorenz.

L'année suivante, Mitchell Feigenbaum a publié l'article noté "quantitative Universalité pour une classe de transformations non linéaires", où il décrit cartes logistiques. Feigenbaum avait appliqué la géométrie fractale pour l'étude des formes naturelles telles que les côtes. Feigenbaum notamment découvert l'universalité dans le chaos, ce qui permet une application de la théorie du chaos à de nombreux phénomènes différents.

En 1979, Albert J. Libchaber, lors d'un colloque organisé à Aspen par Pierre Hohenberg, a présenté son observation expérimentale de la bifurcation cascade qui mène au chaos et la turbulence dans convective Systèmes de Rayleigh-Bénard. Il a reçu le Prix Wolf de physique en 1986 avec Mitchell J. Feigenbaum "pour sa brillante démonstration expérimentale de la transition vers la turbulence et le chaos dans les systèmes dynamiques".

Le New York Academy of Sciences a ensuite co-organisé, en 1986, avec le Institut national de la santé mentale et la Office of Naval Research la première conférence importante sur le chaos en biologie et en médecine. Bernardo Huberman ainsi présenté un modèle mathématique de la oeil trouble de suivi chez les schizophrènes . La théorie du chaos par la suite renouvelé physiologie dans les années 1980, par exemple dans l'étude des pathologique cycles cardiaques.

En 1987, Par Bak, Chao Tang et Kurt Wiesenfeld publié un article dans Lettres de Physical Review décrivant pour la première fois auto-organisé criticité (SOC), considéré comme l'un des mécanismes par lesquels complexité tient dans la nature. Parallèlement aux approches largement laboratoire à base tels que la Bak-Tang-Wiesenfeld sandpile, de nombreuses autres enquêtes ont centré autour de systèmes naturels ou sociaux à grande échelle qui sont connus (ou présumés) pour afficher échelle invariant comportement. Bien que ces approches ne ont pas toujours les bienvenus (au moins au début) par des spécialistes dans les sujets examinés, SOC a néanmoins se établir comme un bon candidat pour expliquer un certain nombre de phénomènes naturels, y compris: les tremblements de terre (qui, bien avant SOC a été découvert, étaient connus comme source de comportement échelle invariant comme le La loi de Gutenberg-Richter décrivant la distribution statistique des tailles du tremblement de terre, et de la Omori loi décrivant la fréquence des répliques); éruptions solaires; fluctuations dans les systèmes économiques tels que marchés financiers (références à SOC sont communs dans éconophysique); la formation du paysage; les incendies de forêt; glissements de terrain; épidémies; et l'évolution biologique (où SOC a été invoqué, par exemple, que le mécanisme dynamique derrière la théorie du «équilibres ponctués» mis en avant par Niles Eldredge et Stephen Jay Gould ). Inquiétant, étant donné les implications d'une distribution gratuite échelle de tailles d'événements, certains chercheurs ont suggéré que un autre phénomène qui devrait être considéré comme un exemple de la SOC est l'apparition de guerres . Ces enquêtes "appliquées" de SOC ont inclus deux tentatives de modélisation (soit le développement de nouveaux modèles ou d'adapter ceux qui existent déjà aux spécificités d'un système naturel donné), et l'analyse des données approfondies pour déterminer l'existence et / ou caractéristiques des lois d'échelle naturelles.

La même année, James Gleick publié Chaos: Making une nouvelle science, qui est devenu un best-seller et a introduit les principes généraux de la théorie du chaos, ainsi que son histoire au grand public. Au début, les domaines de travail de quelques individus isolés,, la théorie du chaos progressivement émergé comme un transdisciplinaire et la discipline institutionnelle, principalement sous le nom de l'analyse des systèmes non linéaire. Faisant allusion à Thomas Kuhn notion d 'un changement de paradigme exposé dans La Structure des révolutions scientifiques (1962), de nombreux «chaologists» (comme certains se auto-nommé) a affirmé que cette nouvelle théorie était un exemple d'un tel changement, une thèse défendue par J. Gleick.

La disponibilité des ordinateurs moins chers, plus puissants élargit l'applicabilité de la théorie du chaos. Actuellement, la théorie du chaos continue d'être un domaine de recherche très actif, impliquant de multiples disciplines (mathématiques, la topologie , la physique, la biologie des populations, la biologie, la météorologie, l'astrophysique, théorie de l'information, etc.).

Dynamique chaotique

Pour un système dynamique d'être classé comme chaotique, il doit avoir les propriétés suivantes:

• il doit être sensible aux conditions initiales,
• ce doit être topologiquement mélange, et
• son orbites périodiques doivent être dense.

Sensibilité aux conditions initiales signifie que chaque point dans un tel système est arbitrairement étroitement approchée par d'autres points avec sensiblement différentes trajectoires futures. Ainsi, une petite perturbation arbitraire de la trajectoire actuelle peut conduire à un comportement futur significativement différente.

Sensibilité aux conditions initiales est populairement connu sous le nom " l'effet papillon », ainsi appelé parce que le titre d'un document donné par Edward Lorenz en 1972 à la Association américaine pour l'avancement des sciences à Washington, DC prévisibilité intitulé: le battement d'ailes d'un papillon au Brésil Est a déclenché une tornade au Texas Le battement des ailes représente un petit changement dans l'état initial du système, ce qui provoque une chaîne de? événements qui ont conduit à des phénomènes à grande échelle. Le papillon avait pas battit ses ailes, la trajectoire du système aurait pu être très différent.

Sensibilité aux conditions initiales est souvent confondu avec le chaos dans les récits populaires. Il peut aussi être une propriété subtile, car il dépend d'un choix de métrique, ou la notion de distance dans le l'espace de phase du système. Par exemple, considérons le système dynamique simple, produite en doublant à plusieurs reprises une valeur initiale (définie par la cartographie sur la ligne réelle de x à 2x). Ce système a dépendance sensible aux conditions initiales partout, depuis ne importe quelle paire de points à proximité finira par devenir largement séparés. Cependant, il présente un comportement extrêmement simple, car tous les points à l'exception de 0 tendent vers l'infini. Si à la place, nous utilisons la métrique bornée sur la ligne obtenue en additionnant le point à l'infini et l'affichage le résultat comme un cercle, le système ne est plus sensible aux conditions initiales. Pour cette raison, dans la définition de chaos, l'attention est normalement limitée à des systèmes avec des métriques bornées, ou fermé, délimité sous-ensembles invariants des systèmes non bornés.

Même pour les systèmes bornées, sensibilité aux conditions initiales ne est pas identique avec le chaos. Par exemple, considérez le tore à deux dimensions décrites par une paire d'angles (X, Y), chaque comprise entre zéro et 2π. Définir un mappage qui prend tout point (x, y) (2x, y + a), où a est un nombre quelconque tel que a / 2π est irrationnel. Parce que du doublement de la première coordonnée, la cartographie présente dépendance sensible aux conditions initiales. Toutefois, en raison de la rotation irrationnel dans la seconde coordonnée, il n'y a pas orbites périodiques, et par conséquent ne est pas le mappage chaotique selon la définition ci-dessus.

Mélange topologiquement signifie que le système va évoluer au fil du temps de sorte que toute région ou ouvert de son espace de phase finira par se chevaucher avec toute autre région donnée. Ici, "mélange" est vraiment destiné à correspondre à l'intuition standard: le mélange de couleur des colorants ou des fluides est un exemple d'un système chaotique.

Attracteurs

Certains systèmes dynamiques chaotiques sont partout (voir par exemple Difféomorphismes Anosov), mais dans de nombreux cas un comportement chaotique ne se trouve que dans un sous-ensemble de l'espace de phase. Les cas les plus intéressantes se produisent lorsque le comportement chaotique a lieu sur une attracteur, depuis un grand ensemble de conditions initiales conduira à des orbites qui convergent vers cette région chaotique.

Un moyen facile de visualiser un attracteur chaotique est de commencer avec un point dans le bassin d'attraction de l'attracteur, et puis tout simplement tracer son orbite suivante. En raison de la condition de transitivité topologique, ce est susceptible de produire une image de l'ensemble attracteur finale.

Diagramme de phase pour un amorti entraîné pendule, avec double mouvement période

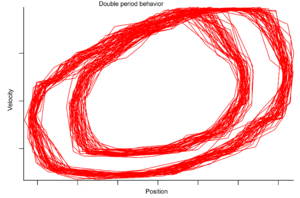
Par exemple, dans un système qui décrit une pendule, l'espace des phases peut être à deux dimensions, comprenant des informations sur la position et la vitesse. On peut tracer la position d'un pendule contre sa vitesse. Un pendule au repos sera tracé comme un point, et l'autre dans un mouvement périodique sera tracé comme une courbe fermée simple. Quand un tel tracé forme une courbe fermée, la courbe est appelé un orbite. Notre pendule a un nombre infini de ces orbites, formant un crayon d'ellipses imbriquées sur l'origine.

Attracteurs étranges

Alors que la plupart des types de mouvement mentionnés ci-dessus donnent lieu à des attracteurs très simples, tels que les points et les courbes de cercle comme appelés cycles limites, mouvement chaotique donne lieu à ce qu'on appelle les attracteurs étranges, attracteurs qui peuvent avoir beaucoup de détails et la complexité. Par exemple, un modèle tridimensionnel simple de la Lorenz système météorologique donne lieu à la célèbre Attracteur de Lorenz. L'attracteur de Lorenz est peut-être l'un des schémas de systèmes chaotiques les plus connus, probablement parce que non seulement il était l'un des premiers, mais il est l'un des plus complexe et en tant que telle donne lieu à un modèle très intéressant qui ressemble à des ailes de un papillon. Un autre exemple est l'attracteur Carte Rössler, qui connaît période de deux parcours de doublement au chaos, comme la carte logistique.

Attracteurs étranges se produisent à la fois systèmes continus (tels que le système de Lorenz) et dans certaines systèmes discrets (tels que la Carte Hénon). D'autres systèmes dynamiques discrets ont une structure de répulsion appelé Ensemble de Julia qui se forme à la limite entre les bassins d'attraction des points fixes - ensembles de Julia peut être considéré comme repellers étranges. Les deux attracteurs étranges et ensembles de Julia ont généralement une fractale structure.

Le Poincaré-Bendixson théorème montre que un attracteur étrange ne peut se produire dans un système dynamique continu se il a trois ou plusieurs dimensions. Toutefois, aucune restriction ne se applique aux systèmes discrets, qui peuvent présenter attracteurs étranges dans deux ou même les systèmes unidimensionnels.

Les conditions initiales de trois ou plusieurs organismes qui interagissent par l'attraction gravitationnelle (voir la n problème -Corps) peut être agencé de manière à produire un mouvement chaotique.

La complexité minimum d'un système chaotique

Bifurcation schéma d'une carte logistique, affichant un comportement chaotique passé un seuil

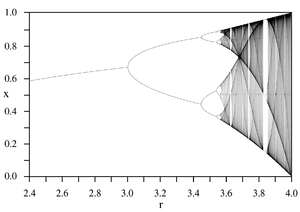
Des systèmes simples peuvent également produire le chaos sans compter sur les équations différentielles . Un exemple est le logistique carte, qui est une équation de différence ( relation de récurrence) qui décrit la croissance de la population au fil du temps.

Même l'évolution des systèmes discrets simples, tels que automates cellulaires, peuvent fortement dépendre des conditions initiales. Stephen Wolfram a enquêté sur un automate cellulaire avec cette propriété, appelée par lui règle 30.

Un modèle minimal pour conservatrice (réversible) comportement chaotique est fourni par Cat la carte de Arnold.

Théorie mathématique

Le théorème de Sarkovskii est à la base du Li et Yorke (1975) de la preuve que tout système à une dimension qui présente un cycle régulier de période affichera également trois cycles réguliers de chaque autre longueur ainsi que des orbites complètement chaotiques.

Les mathématiciens ont mis au point de nombreuses autres façons de faire des déclarations quantitatives sur les systèmes chaotiques. Ceux-ci comprennent: dimension fractale de l'attracteur, Exposants de Lyapunov, parcelles de récurrence, Cartes de Poincaré, diagrammes de bifurcation, et opérateur de transfert.

Distinguer aléatoire à partir des données chaotique

Il peut être difficile de dire à partir de données si un processus observé physique ou autre est aléatoire ou chaotique, car en pratique, pas de séries chronologiques se compose de pur «signal». Il y aura toujours une certaine forme de bruit corruptrice, même se il est présent comme arrondi ou erreur de troncature. Ainsi une série en temps réel, même si la plupart du temps déterministe, contiendra un peu de hasard.

Toutes les méthodes pour distinguer les processus déterministe et stochastique se appuient sur le fait qu'un système déterministe évolue toujours de la même manière à partir d'un point de départ donné. Ainsi, étant donné une série de temps pour tester le déterminisme, on peut:

1. choisir un état de test;
2. rechercher la série de temps pour un état similaire ou «à proximité»; et
3. comparer leurs évolutions temporelles respectives.

Définir l'erreur comme la différence entre l'évolution temporelle de l'état "test" et l'évolution dans le temps de l'état à proximité. Un système déterministe aura une erreur qui soit reste petite (stable, solution régulière) ou augmente de façon exponentielle avec le temps (le chaos). Système stochastique aura une erreur distribuées au hasard.

Essentiellement toutes les mesures prises à partir du déterminisme séries chronologiques reposent sur trouver les états les plus proches à un état donné "test" (ce est à dire, dimension de corrélation, les exposants de Lyapunov, etc.). Pour définir l'état d'un système on se fie généralement sur l'espace des phases méthodes d'enrobage. Typiquement on choisit une dimension d'intégration, et étudie la propagation de l'erreur entre deux états voisins. Si l'erreur semble aléatoire, on augmente la dimension. Si vous pouvez augmenter la dimension d'obtenir une erreur en regardant déterministe, alors vous êtes fait. Même si cela peut paraître simple, il ne est pas vraiment. Une complication est que la dimension augmente la recherche d'un état à proximité nécessite beaucoup plus de temps de calcul et beaucoup de données (la quantité de données nécessaire augmente de façon exponentielle avec la dimension intégration) de trouver un candidat convenable à proximité. Si la dimension d'intégration (nombre de mesures par l'État) est choisie trop petite (inférieure à la valeur 'true') des données déterministes peuvent sembler aléatoire mais en théorie il n'y a aucun problème en choisissant la dimension trop grande - la méthode va fonctionner. Pratiquement, quelque chose d'approchant environ 10 dimensions est considérée comme si importante que une description stochastique est probablement plus approprié et pratique de toute façon.

Applications

La théorie du chaos est appliqué dans de nombreuses disciplines scientifiques: mathématiques , la biologie , l'informatique , l'économie , l'ingénierie , la finance , la philosophie , la physique , la politique , la dynamique des populations, la psychologie , et robotique.

La théorie du chaos est également actuellement appliqué aux études médicales de l'épilepsie , en particulier à la prévision des crises apparemment aléatoires en observant les conditions initiales.

Littérature

Articles

• Li, et TY Yorke, le juge «Période Trois Implique Chaos." American Mathematical Monthly 82, 985-992, 1975.
• Kolyada, SF «Sensibilité Li-Yorke et d'autres concepts du chaos", Math ukrainienne. J. 56 (2004), de 1242 à -1257.
• CE Shannon, " Une théorie mathématique de la communication ", Système de Bell Technical Journal, vol. 27, pp. 379-423, 623-656, Juillet, Octobre, 1948

Manuels

• Alligood, KT (1997) Chaos:. Une introduction aux systèmes dynamiques. Springer-Verlag New York, LLC. ISBN 0-387-94677-2.
• Baker, GL (1996). Chaos, diffusion et mécanique statistique. Cambridge University Press. ISBN 0-521-39511-9.
• Badii, R .; A. Politi (1997). "Complexité: structures hiérarchiques et mise à l'échelle en physique". Cambridge University Press. ISBN 0521663857. http://www.cambridge.org/catalogue/catalogue.asp?isbn=0521663857.
• Devaney, Robert L. (2003). Introduction à Chaotic systèmes dynamiques, 2e éd,. Westview Press. ISBN 0-8133-4085-3.
• Gollub, JP; Baker, GL (1996). Dynamique chaotique. Cambridge University Press. ISBN 0-521-47685-2.
• Gutzwiller, Martin (1990). Chaos en mécanique classique et quantique. Springer-Verlag New York, LLC. ISBN 0-387-97173-4.
• Hoover, William Graham (1999,2001). Durée Réversibilité, simulation par ordinateur, et le Chaos. Monde scientifique. ISBN 981-02-4073-2.
• Kiel, L. Douglas; Elliott, Euel W. (1997). Théorie du Chaos dans les sciences sociales. Perseus Publishing. ISBN 0-472-08472-0.
• Lune, Francis (1990). Chaotic Dynamics et fractale. Springer-Verlag New York, LLC. ISBN 0-471-54571-6.
• Ott, Edward (2002). Chaos dans les systèmes dynamiques. Cambridge University Press, New, York. ISBN 0-521-01084-5.
• Strogatz, Steven (2000). Dynamique non linéaire et le chaos. Perseus Publishing. ISBN 0-7382-0453-6.
• Sprott, Julien Clinton (2003). Chaos et de l'analyse des séries chronologiques. Oxford University Press. ISBN 0-19-850840-9.
• Tél, Tamás; Gruiz, Márton (2006) Dynamique chaotique:. Une introduction sur la base de la mécanique classique. Cambridge University Press. ISBN 0-521-83912-2.
• Tufillaro, Abbott, Reilly (1992). Une approche expérimentale à la dynamique et le chaos non linéaires. Addison-Wesley New York. ISBN 0-201-55441-0.
• Zaslavsky, George M. (2005). Hamiltonien Chaos et fractions Dynamics. Oxford University Press. ISBN 0-198-52604-0.

Œuvres semi-technique et populaires

• Ralph H. Abraham et Yoshisuke Ueda (Ed.), Le Chaos Avant-Garde: Mémoires des premiers jours de la théorie du chaos, World Scientific Publishing Company, 2001, 232 pp.
• Michael Barnsley, fractales Partout, Academic Press 1988, 394 pp.
• Richard J Bird, Chaos et de la vie: la complexité et de l'Ordre dans l'évolution et la Pensée, Columbia University Press 2003, 352 pp.
• John Briggs et David Peat, Turbulent Mirror: An Illustrated Guide à la théorie du chaos et de la science de la Totalité, Harper Perennial 1990, 224 pp.
• John Briggs et David Peat, Sept leçons de vie: Chaos sagesse spirituelle de la science du changement, Harper Perennial 2000, 224 pp.
• Lawrence A. Cunningham, de Random Walks à Chaotic Crashes: La Généalogie linéaire de l'Efficient Capital Market Hypothesis, George Washington Law Review, vol. 62, 1994, 546 pp.
• Leon Glass et Michael C. Mackey, des horloges à Chaos: des rythmes de vie, Princeton University Press 1988, 272 pp.
• James Gleick, Chaos: Making une nouvelle science, New York: Penguin, 1988. 368 pp.
• John Gribbin, Deep Simplicité,
• L Douglas Kiel, Euel W Elliott (éd.), Théorie du Chaos dans les sciences sociales: fondements et applications, University of Michigan Press, 1997, 360 pp.
• Arvind Kumar, Chaos, fractales et l'auto-organisation; Nouvelles perspectives sur la complexité de la nature, National Book Trust, 2003.
• Hans Lauwerier, Fractales, Princeton University Press, 1991.
• Edward Lorenz, l'Essence of Chaos, University of Washington Press, 1996.
• Heinz-Otto Peitgen et Dietmar Saupe (Eds.), La Science des images fractales, Springer 1988, 312 pp.
• Clifford A. Pickover, Ordinateurs, Motif, Chaos, et beauté: Graphics à partir d'un monde invisible, St Martins Pr 1991.
• Ilya Prigogine et Isabelle Stengers, l'ordre du chaos, Bantam 1984.
• H.-O. Peitgen et PH Richter, La beauté de Fractales: Images de complexes systèmes dynamiques, Springer 1986, 211 pp.
• David Ruelle, Chance et le Chaos, Princeton University Press, 1993.
• David Ruelle, Chaotic Evolution et Strange Attractors, Cambridge University Press, 1989.
• Peter Smith, Expliquer Chaos, Cambridge University Press, 1998.
• Ian Stewart, Dieu joue-t Dice ?: The Mathematics of Chaos, Blackwell Publishers, 1990.
• Steven Strogatz, Sync: La science émergente de l'ordre spontané, Hyperion, 2003.
• Yoshisuke Ueda, The Road To Chaos, Pr aérienne, 1993.
• M. Mitchell Waldrop, Complexité: la nouvelle science au bord de l'Ordre et du Chaos, Simon & Schuster, 1992.