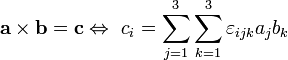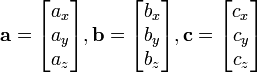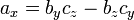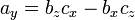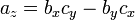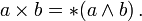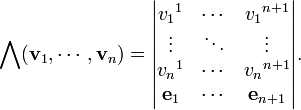Produit Croix
Renseignements généraux
Cette sélection se fait pour les écoles par la charité pour enfants lire la suite . Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays
En mathématiques , le produit croisé est un opération binaire sur deux vecteurs dans une tridimensionnel euclidien espace qui résulte en un autre vecteur qui est perpendiculaire aux deux vecteurs d'entrée. En revanche, la produit scalaire produit une résultat scalaire. Dans de nombreux problèmes d'ingénierie et de physique, il est pratique de pouvoir construire un vecteur perpendiculaire à partir de deux vecteurs existants, et le produit croisé fournit un moyen pour le faire. Le produit vectoriel est également connu comme le produit vectoriel ou Gibbs produit vectoriel.
Le produit cartésien ne est pas défini, sauf dans les trois dimensions (et le algèbre définie par le produit croix ne est pas associative ). Comme le produit scalaire, cela dépend de la métrique de l'espace euclidien. Contrairement à la produit scalaire, cela dépend aussi sur le choix des l'orientation ou "impartialité". Certaines fonctionnalités du produit croix peuvent être généralisés à d'autres situations. Pour des choix arbitraires de l'orientation, le produit croisé doit pas être considérée comme un vecteur, mais comme un pseudovector. Pour des choix arbitraires de métrique, et dans des dimensions arbitraires, le produit croisé peut être généralisée par la produit extérieur de vecteurs, la définition d'une deux-forme au lieu d'un vecteur.
Définition
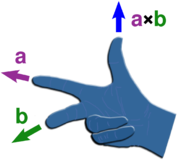
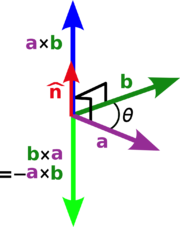
Le produit vectoriel de deux vecteurs A et B est désigné par a × b. Dans un tridimensionnelle espace euclidien , avec une habitude système droitier coordonner , il est défini comme un vecteur qui est c perpendiculaire à la fois A et B, avec une direction donnée par le Règle de la main droite et une grandeur égale à la surface de la parallélogramme que les vecteurs couvrent.
Le produit vectoriel est donné par la formule
où θ est la mesure de l' angle entre a et b (0 ° ≤ θ ≤ 180 °), a et b sont les grandeurs de vecteurs a et b, et 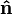 est un vecteur unitaire perpendiculaire au plan contenant a et b. Si les vecteurs a et b sont colinéaires (c.-à θ l'angle entre les deux est de 0 ° ou 180 °), par la formule ci-dessus, le produit vectoriel de a et b est le vecteur nul 0.
est un vecteur unitaire perpendiculaire au plan contenant a et b. Si les vecteurs a et b sont colinéaires (c.-à θ l'angle entre les deux est de 0 ° ou 180 °), par la formule ci-dessus, le produit vectoriel de a et b est le vecteur nul 0.
La direction du vecteur 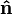 est donnée par la règle de droite, où on rappelle simplement l'index de la main droite dans le sens d'un et le doigt du milieu dans le sens de b. Puis, le vecteur
est donnée par la règle de droite, où on rappelle simplement l'index de la main droite dans le sens d'un et le doigt du milieu dans le sens de b. Puis, le vecteur 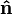 qui sort du pouce (voir l'image à droite).
qui sort du pouce (voir l'image à droite).
Utilisation de l'appareil nécessite la chiralité transversale du système de coordonnées à prendre en compte (comme explicite dans la définition ci-dessus). Si un gaucher système de coordonnées est utilisé, la direction du vecteur 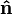 est donnée par la règle de gauche et des points dans la direction opposée.
est donnée par la règle de gauche et des points dans la direction opposée.
Ceci, cependant, crée un problème parce que la transformation d'un système de référence arbitraire à un autre (par exemple, une transformation d'image miroir d'un droitier à un système gaucher coordonner), ne devrait pas changer la direction de 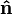 . Le problème est clarifié par se rendre compte que le produit croisé de deux vecteurs ne est pas un (vrai) vecteur, mais plutôt un pseudovector. Voir produit croix et impartialité pour plus de détails.
. Le problème est clarifié par se rendre compte que le produit croisé de deux vecteurs ne est pas un (vrai) vecteur, mais plutôt un pseudovector. Voir produit croix et impartialité pour plus de détails.
Le calcul du produit vectoriel
Coordonner la notation
Le des vecteurs d'unité i, j et k du système de coordonnées orthogonal donné satisfont les égalités suivantes:
- i × j = k j × k = i k × i = j.
Avec ces règles, les coordonnées du produit croisé de deux vecteurs peuvent être calculées facilement, sans la nécessité de déterminer les angles: Let
- A = A 1 + i + j 2 3 k = (a 1, a 2, a 3)
et
- b = b 1 i + b 2 j + b 3 k = (b 1, b 2, b 3)
Puis
- a × b = (2 b 3 - 3 b 2) i + (3 b 1 - un 1 b 3) j + (A 1 B 2 - 2 b 1) k = (2 b 3 - un 3 b 2, 3 b 1 - un 1 b 3, un 1 b 2 - 2 b 1)
notation matricielle
La notation de coordonnées peut aussi se écrire formellement que le facteur déterminant d'une matrice :
Le déterminant de trois vecteurs peut être récupéré que
- det (a, b, c) = a · (b × c).
Intuitivement, le produit vectoriel peut être décrit par Le régime de Sarrus. Considérons la table
Pour les trois premiers vecteurs unitaires, multiplier les éléments de la diagonale vers la droite (par exemple, la première diagonale contiendrait i, a 2, et b 3). Pour les trois derniers vecteurs unitaires, multiplier les éléments sur la diagonale vers la gauche et ensuite nier le produit (par exemple, la dernière diagonale contiendrait k, 2, et b 1). Le produit vectoriel serait défini par la somme de ces produits:
Bien écrit ici en termes de coordonnées, il résulte de la définition géométrique ci-dessus que le produit croisé est invariant sous rotations autour de l'axe défini par une × b, et flips signe sous permutation a et b.
Exemples
Exemple 1
Considérons deux vecteurs, a = (1,2,3) et b = (4,5,6). Le produit une croix × b est
- a × b = (1,2,3) x (4,5,6) = ((2 x 6-3 x 5), - (1 x 6-3 x 4), + (1 x 5 - 2 × 4)) = (-3,6, -3).
Exemple 2
Considérons deux vecteurs, a = (3,0,0) et b = (0,2,0). Le produit une croix × b est
- a × b = (3,0,0) x (0,2,0) = ((x 0 0 - 0 x 2), (x 0 0-3 x 0), (3 x 2 - 0 x 0) ) = (0,0,6).
Cet exemple présente les interprétations suivantes:
- L'aire du parallélogramme (un rectangle dans le cas présent) est de 2 x 3 = 6.
- Le produit vectoriel de deux vecteurs quelconques dans le plan xy sera parallèle à l'axe z.
- Depuis la composante z du résultat est positif, l'angle obtus non de A à B est le sens antihoraire (quand on l'observe d'un point sur le + demi-axe z, et lorsque le système de coordonnées est droitier).
Propriétés
Sens géométrique
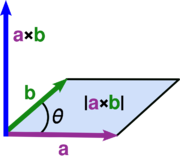
L'ampleur du produit vectoriel peut être interprétée comme la non signé domaine de la parallélogramme ayant a et b côtés:
En effet, on peut également calculer le volume V d'un parallélépipédique comportant a, b et c que les côtés en utilisant une combinaison d'un produit vectoriel et un produit scalaire, appelée produit scalaire triple:
Propriétés algébriques
Le produit vectoriel est anticommutative,
- a × b = - b × a,
distributive sur l'addition,
- a × (b + c) = (a × b) + (a × c),
et compatible avec multiplication scalaire sorte que
- (R a) × × b = a (R b) = r (a × b).
Il ne est pas associative , mais satisfait la Jacobi identité:
- a × (b × c) + b × (c × a) + c × (axb) = 0.
Il ne obéit pas à la le droit d'annulation:
- Si une × b = a × c et a ≠ 0, alors on peut écrire:
- (A × b) - (a × c) = 0 et, par la loi distributive ci-dessus:
- a × (b - c) = 0
- Maintenant, si un est parallèle à (B - C), alors, même si a ≠ 0, il est possible que (B - C) ≠ 0 et donc que b ≠ c.
Toutefois, si à la fois un · b = a · c et a × b = a × c, alors nous pouvons conclure que b = c. En Effet,
- a. (B - c) = 0, et
- a × (b - c) = 0
de sorte que b - c est à la fois parallèle et perpendiculaire au vecteur non nul a. Ceci ne est possible que si b - c = 0.
La distributivité, linéarité et Jacobi spectacle identité que R 3 avec l'addition de vecteurs et le produit forme une croix Algèbre de Lie.
En outre, deux vecteurs non nuls a et b sont parallèles ssi a × b = 0.
Triple expansion du produit
L'expansion du produit triple, aussi connu comme la formule de Lagrange, est une formule reliant le produit vectoriel de trois vecteurs (appelé le vecteur produit triple) avec le produit scalaire:
- A × (B × C) = b (un · c) - c (a · b).
Le "BAC moins CAB" mnémonique est utilisée pour mémoriser l'ordre des vecteurs dans l'élément de la main droite. Cette formule est utilisée en physique pour simplifier les calculs vectoriels. Un cas particulier, en ce qui concerne gradients et utile dans le calcul vectoriel , est donnée ci-dessous.
Ce est un cas particulier de la plus générale Opérateur de Laplace-de Rham 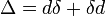 .
.
L'identité suivante concerne également le produit croix et le produit scalaire:
Ce est un cas particulier de la multiplicativité 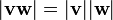 de la norme dans le quaternion algèbre, et une restriction à
de la norme dans le quaternion algèbre, et une restriction à 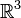 de Identité de Lagrange.
de Identité de Lagrange.
Autres moyens de calculer le produit croisé
Quaternions
Le produit croisé peut également être décrite en termes de quaternions, et ce est pourquoi les lettres i, j, k sont une convention pour la base standard sur 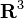 : Il est considéré comme les quaternions imaginaires.
: Il est considéré comme les quaternions imaginaires.
Avis par exemple, que les relations de produits ci-dessus données croisées entre i, j, k et d'accord avec les relations multiplicatives entre les quaternions i, j, k. En général, si nous représentons un vecteur [A 1, A 2, 3] comme un quaternion 1 i + 2 j + 3 k, on obtient le produit croisé de deux vecteurs en prenant leur produit comme quaternions et la suppression du partie réelle du résultat. La partie réelle sera le négatif de la point produit des deux vecteurs.
La conversion à la multiplication de matrices
Un produit vectoriel entre les deux vecteurs (qui ne peut être défini dans un espace tridimensionnel) peut être réécrite en termes de multiplication de la matrice pure comme le produit d'une antisymétrique matrice et un vecteur, comme suit:
où
En outre, si 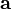 est elle-même un produit en croix:
est elle-même un produit en croix:
puis
Cette notation constitue une autre façon de généraliser produit en croix aux dimensions supérieures en substituant pseudovectors (tels que vitesse angulaire ou champ magnétique) avec de telles matrices antisymétriques. Il est clair que de telles quantités physiques auront n (n-1) / 2 composantes indépendantes en n dimensions, qui coïncide avec le nombre de dimensions de l'espace à trois dimensions, et ce est pourquoi vecteurs peuvent être utilisés (et le plus souvent sont utilisés) pour représenter de telles quantités.
Cette notation est souvent beaucoup plus facile de travailler avec, par exemple, dans géométrie épipolaire.
Dans les propriétés générales du produit croix suit immédiatement que
![[\ Mathbf {a}] _ {\ times} \, \ mathbf {a} = \ mathbf {0}](../../images/212/21241.png) et
et ![\ Mathbf {a} ^ {T} \ [\ mathbf {a}] _ {\ times} = \ mathbf {0}](../../images/212/21242.png)
et de fait que ![[\ Mathbf {a}] _ {\ times}](../../images/212/21243.png) est antisymétrique il se ensuit que
est antisymétrique il se ensuit que
L'expansion de triple produit mentionné ci-dessus (règle bac cabine) peut être facilement prouvé en utilisant cette notation.
La définition ci-dessus ![[\ Mathbf {a}] _ {\ times}](../../images/212/21243.png) signifie qu'il ya un mappage un-à-un entre l'ensemble des trois matrices × 3 antisymétriques, également notée SO (3), et le fonctionnement de la prise du produit avec un vecteur croix
signifie qu'il ya un mappage un-à-un entre l'ensemble des trois matrices × 3 antisymétriques, également notée SO (3), et le fonctionnement de la prise du produit avec un vecteur croix 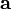 .
.
Indice de notation
Le produit croix peut aussi être défini en termes de Levi-Civita tenseur 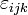
où les indices 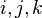 correspondre, comme dans la section précédente, à composantes vectorielles orthogonales.
correspondre, comme dans la section précédente, à composantes vectorielles orthogonales.
Mnémonique
Le mot xyzzy peut être utilisée pour rappeler la définition du produit vectoriel.
Si
où:
alors:
Remarquez que les deuxième et troisième équations peuvent être obtenus à partir de la première par une simple rotation verticalement les indices, x → y → x → z. Le problème, bien sûr, est de savoir comment se souvenir de la première équation, et deux options sont disponibles à cet effet: soit vous vous souvenez des deux diagonales pertinentes du schéma Sarrus (ceux contenant i), ou vous souvenez de la xyzzy séquence.
Depuis la première diagonale dans le schéma de Sarrus est que le diagonale principale du dessus -mentioned 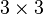 matrice, les trois premières lettres du mot xyzzy peut être très facile à retenir.
matrice, les trois premières lettres du mot xyzzy peut être très facile à retenir.
Applications
Géométrie algorithmique
Le produit vectoriel peut être utilisé pour calculer la normale pour un triangle ou un polygone, une opération fréquemment réalisée dans infographie.
En de calcul de la géométrie du plan , le produit vectoriel est utilisé pour déterminer le signe de l' angle aigu défini par trois points 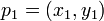 ,
, 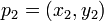 et
et 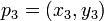 . Elle correspond à la direction du produit vectoriel des deux coplanaires vecteurs définis par les paires de points
. Elle correspond à la direction du produit vectoriel des deux coplanaires vecteurs définis par les paires de points 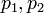 et
et 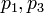 , Ce est à dire, par le signe de l'expression
, Ce est à dire, par le signe de l'expression 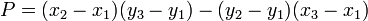 . Dans le système "droitier" coordonner, si le résultat est 0, les points sont alignés; si elle est positive, les trois points forment un angle négatif de rotation autour de
. Dans le système "droitier" coordonner, si le résultat est 0, les points sont alignés; si elle est positive, les trois points forment un angle négatif de rotation autour de 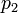 à partir de
à partir de 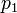 à
à 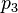 , Sinon un angle positif. D'un autre point de vue, le signe de
, Sinon un angle positif. D'un autre point de vue, le signe de 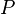 indique si
indique si 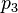 se trouve à gauche ou à droite de la ligne
se trouve à gauche ou à droite de la ligne 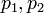 .
.
Autre
Le produit croisé se produit dans la formule de la opérateur vectoriel boucle. Il est également utilisé pour décrire le Force de Lorentz vécue par une charge électrique se déplaçant dans un champ magnétique. Les définitions de couple et moment angulaire impliquent également le produit croisé.
L'astuce de réécrire un produit transversale en termes d'une multiplication de matrice apparaît fréquemment dans épipolaire et multi-géométrie de la vue, en particulier lors de la dérivation contraintes correspondant.
Produit Croix comme un produit extérieur
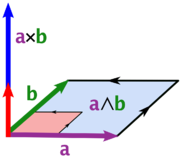
Le produit croix peut être considérée en termes de produit extérieur. Ce point de vue permet une interprétation géométrique naturelle du produit croix. En extérieur calcul formel du produit extérieur (ou produit de coin) de deux vecteurs est une bivecteur. Un bivecteur est un élément plan orienté, de la même manière qu'un vecteur est un élément de ligne orienté. Étant donné deux vecteurs a et b, on peut voir le bivecteur a ∧ b que le parallélogramme orienté engendré par a et b. Le produit vectoriel est alors obtenue en prenant la Hodge dual du bivecteur a ∧ b, identifier Deux vecteurs avec des vecteurs:
Cela peut être considéré comme l'élément multi-dimensionnelle orientée "perpendiculaire" à l'bivecteur. Seulement en trois dimensions est le résultat d'un élément orienté ligne - un vecteur - alors que, par exemple, en 4 dimensions Hodge dual d'un bivecteur est à deux dimensions - un autre élément de plan orienté. Ainsi, en trois dimensions ne est le produit vectoriel de a et b du vecteur double pour le bivecteur a ∧ b: il est perpendiculaire au bivecteur, avec l'orientation dépend de la chiralité du système de coordonnées, et a la même amplitude par rapport à l'unité normale un vecteur tel que ∧ b a par rapport au bivecteur unitaire; précisément les propriétés décrites ci-dessus.
Produit Cross et impartialité
Lorsque des quantités mesurables concernent des produits croisés, l'impartialité des systèmes de coordonnées utilisés ne peut être arbitraire. Cependant, lorsque les lois de la physique sont écrites comme des équations, il devrait être possible de faire un choix arbitraire du système de coordonnées (y compris l'impartialité). Pour éviter les problèmes, il faut être prudent de ne jamais écrire une équation où les deux parties ne se comportent pas également dans toutes les transformations qui doivent être pris en considération. Par exemple, si une partie de l'équation est le produit vectoriel de deux vecteurs, il faut prendre en compte que lorsque la chiralité du système de coordonnées ne est pas fixée a priori, le résultat ne est pas un (true) mais un vecteur pseudovector. Par conséquent, par souci de cohérence, de l'autre côté doit également être un pseudovector.
Plus généralement, le résultat d'un produit croisé peut être un vecteur ou un pseudo-vecteur, en fonction du type de ses opérandes (vecteurs ou pseudovectors). A savoir, les vecteurs et pseudovectors sont liés dans les façons suivantes sous l'application du produit croix:
- vecteur vecteur × = pseudovector
- vecteur × pseudovector = vecteur
- pseudovector × pseudovector = pseudovector
Étant donné que le produit vectoriel peut également être un (true) vecteur, il peut ne pas changer de direction avec une transformation d'image en miroir. Cela se produit, conformément aux relations ci-dessus, si l'un des opérandes est une (true) vecteur et l'autre est un pseudo-vecteur (par exemple, le produit vectoriel de deux vecteurs). Par exemple, un vecteur produit triple impliquant trois vecteurs (vrai) est un (vrai) vecteur.
Une approche libre-impartialité est possible en utilisant algèbre extérieure.
Dimensions supérieures
Il ya plusieurs façons de généraliser le produit croisé aux dimensions supérieures.
Dans le contexte de algèbre multilinéaire, il est possible de définir un produit croisé généralisé en termes de parité de telle sorte que le produit croisé généralisé entre deux vecteurs de dimension n est un antisymétrique tenseur de rang n -2.
Utilisation octonions
Un produit vectoriel des vecteurs de dimension 7 peut être obtenu de la même manière en utilisant le octonions place des quaternions. Le non-existence de ces produits vectoriel de deux vecteurs dans les autres dimensions est lié au résultat que la seule algèbres de division normées sont ceux de dimension 1, 2, 4 et 8.
produit Wedge
En dimension générale, il n'y a pas analogique directe du produit croix binaire. Il ya cependant un Produit en forme de coin, qui a des propriétés similaires, sauf que le produit en forme de coin de deux vecteurs est maintenant 2 vecteur à la place d'un vecteur ordinaire. Comme mentionné ci-dessus, le produit vectoriel peut être interprétée comme le produit de calage en trois dimensions après l'utilisation de la dualité de Hodge identifier deux vecteurs avec des vecteurs.
On peut aussi construire un n analogique -aire du produit croix dans R n 1 donnée par
Cette formule est identique à la structure de la formule déterminant pour le produit croisé normale dans R 3, sauf que la rangée de vecteurs de base est la dernière ligne dans le facteur déterminant plutôt que la première. La raison de ceci est d'assurer que les vecteurs ordonnés (v 1, ..., v n, Λ (v 1, ..., v n)) ont une positif orientation par rapport à (e 1, ..., e n + 1). Si n est pair, cette modification quitte la valeur inchangée, cette convention est d'accord avec la définition normale du produit binaire. Dans le cas où n est impair, toutefois, la distinction doit être maintenue. Ce formulaire n -aire bénéficie d'un grand nombre des mêmes propriétés que le produit vecteur de croix: il est alternant et linéaire dans ses arguments, il est perpendiculaire à chacun des arguments, et son amplitude donne l'hypervolume de la région délimitée par les arguments. Et tout comme le produit vecteur de croix, elle peut être définie dans une coordonnée de manière indépendante comme Hodge double du produit de coin des arguments.
Le produit de calage et produit scalaire peuvent être combinés pour former le Clifford produit.
Histoire
En 1773, Joseph Louis Lagrange introduit la forme composante à la fois le point et produits croisés afin d'étudier le tétraèdre en trois dimensions. En 1843, le physicien mathématique irlandaise Sir William Rowan Hamilton a présenté le produit quaternion, et avec lui les termes "vecteur" et "scalaire". Étant donné deux quaternions [0, u] et [0, v], où u et v sont des vecteurs de R 3, leur produit de quaternion peuvent être résumées comme [- u · v, u × v]. James Clerk Maxwell a utilisé les outils de quaternions de Hamilton de développer ses célèbres équations de l'électromagnétisme , et pour cette raison et d'autres escouades pour un temps étaient une partie essentielle de l'éducation physique.
Cependant, Oliver Heaviside en Angleterre et Josiah Willard Gibbs dans Connecticut a estimé que les méthodes de quaternions étaient trop lourdes, nécessitant souvent la partie scalaire ou vectorielle d'un résultat à extraire. Ainsi, environ quarante ans après que le produit de quaternion, le Produit scalaire et produit vectoriel ont été introduites - à une vive opposition. Pivotal à (éventuelle) acceptation a été l'efficacité de la nouvelle approche, permettant de réduire Heaviside les équations de l'électromagnétisme de l'original de 20 à quatre couramment vu aujourd'hui de Maxwell.
Largement indépendante de ce développement, et largement incompris à l'époque, Hermann Grassmann créé une algèbre géométrique ne est pas liée à la dimension deux ou trois, avec le produit extérieur joue un rôle central. William Kingdon Clifford combiné les algèbres de Hamilton et de Grassmann pour produire Algèbre de Clifford, où dans le cas de trois dimensions vecteurs bivecteur produite à partir de deux vecteurs dualizes à un vecteur, reproduisant ainsi le produit croisé.
La notation croix, qui a commencé avec Gibbs, a inspiré le nom de "produit croisé". Paru à l'origine dans les notes publiées privé pour ses étudiants en 1881 Eléments d'analyse vectorielle, la notation de Gibbs - et le nom - plus tard atteint un plus large public à travers Analyse vectorielle (Gibbs / Wilson), un manuel par un ancien élève. Edwin Bidwell Wilson réarrangé matière de conférences de Gibbs, avec des matières à partir des publications de Heaviside, Föpps et Hamilton. Il a divisé l'analyse vectorielle en trois parties:
- «D'abord, ce qui concerne plus et les produits scalaires et vectoriels de vecteurs. Deuxièmement, ce qui concerne le calcul différentiel et intégral dans ses relations aux fonctions scalaires et vectorielles. Troisièmement, celui qui contient la théorie de la fonction de vecteur linéaire."
Deux principaux types de multiplications vectorielles ont été définis, et ils ont été appelés comme suit:
- La, scalaire ou produit scalaire de deux vecteurs directe
- L'inclinaison, vecteur, produit ou vectoriel de deux vecteurs
Plusieurs types de des produits et des produits de plus de trois vecteurs triples ont également été examinés. L'expansion de triple produit mentionné ci-dessus a également été inclus.


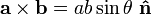
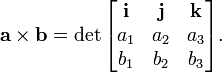
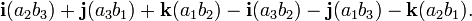
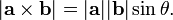
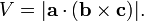
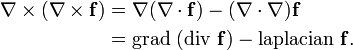
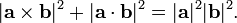
![\ Mathbf {a} \ times \ mathbf {b} = [\ mathbf {a}] _ {\ times} \ mathbf {b} = \ begin {bmatrix} \, 0 & \ -! A_3 & \, \, a_2 \\ \, \, A_3 & 0 & \ -! a_1 \\ - a_2 & \, \, a_1 & \, 0 \ end {bmatrix} \ begin {} bmatrix b_1 \\ \\ b_2 b_3 \ end {} bmatrix](../../images/212/21236.png)
![\ Mathbf {b} \ times \ mathbf {a} = [\ mathbf {a}] ^ T _ {\ times} \ mathbf {b} = \ begin {bmatrix} \, 0 & \, \, A_3 & \ -! A_2 \ \ -a_3 & 0 & \, \, a_1 \\\, \, a_2 & \ -! a_1 & \, 0 \ end {bmatrix} \ begin {} bmatrix b_1 \\ \\ b_2 b_3 \ end {} bmatrix](../../images/212/21237.png)
![[\ Mathbf {a}] _ {\ times} \ stackrel {\ rm def} {} = \ begin {bmatrix} \, \, 0 & \ -! A_3 & \, \, \, a_2 \\\, \, \ , A_3 & 0 & \ -! a_1 \\\ - a_2 & \, \, a_1 & \, \, 0 \ end {} bmatrix.](../../images/212/21238.png)
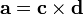
![[\ Mathbf {a}] _ {\ times} = (\ mathbf {c} \ mathbf {d} ^ T) ^ T - \ mathbf {c} \ mathbf {d} ^ T.](../../images/212/21240.png)
![\ Mathbf {b} ^ {T} \ [\ mathbf {a}] _ {\ times} \, \ mathbf {b} = 0.](../../images/212/21244.png)