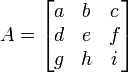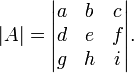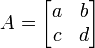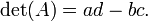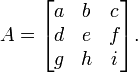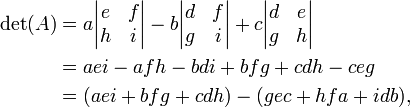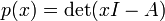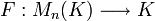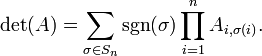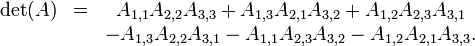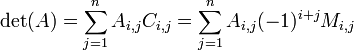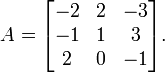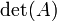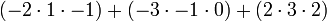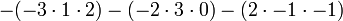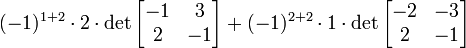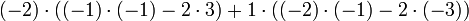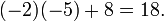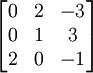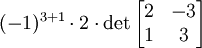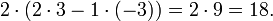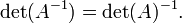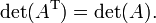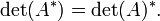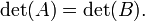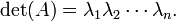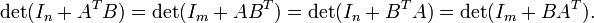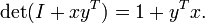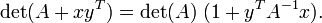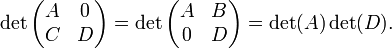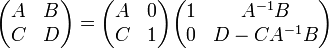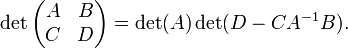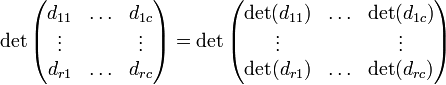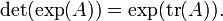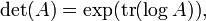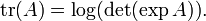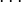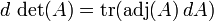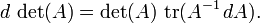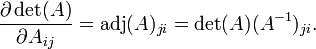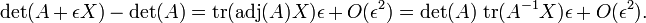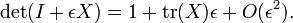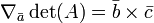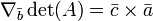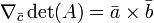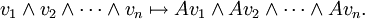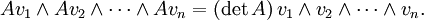Déterminant
Saviez-vous ...
Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet a été une initiative de SOS Enfants. parrainage SOS enfant est cool!
En algèbre , un facteur déterminant est une fonction dépendant de n qui associe un scalaire, det (A), à tous les n × n matrice carrée A. Le sens géométrique fondamentale d'un déterminant est que la facteur d'échelle pour le volume lorsque A est considéré comme un transformation linéaire. Déterminants sont importantes à la fois dans le calcul , où ils entrent dans le règle de substitution pour plusieurs variables, et algèbre multilinéaire.
Pour un entier positif n fixe, il ya une fonction déterminant unique pour l'matrices n × n sur tout anneau commutatif R. En particulier, cette fonction existe lorsque R est le domaine de réels ou des nombres complexes .
Notation barre verticale
Le déterminant de la matrice A est également parfois désignée par | A |. Cette notation peut être ambiguë, car il est également utilisé pour certains les normes de la matrice et de la valeur absolue . Cependant, souvent la norme de la matrice sera notée avec une double barre verticale (par exemple, ‖ ‖ A) et peut porter un indice ainsi. Ainsi, la notation de barre verticale pour déterminant est fréquemment utilisé (par exemple, La règle de Cramer et mineurs). Par exemple, pour la matrice
le déterminant 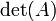 pourrait être indiqué par
pourrait être indiqué par 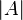 ou de façon plus explicite que
ou de façon plus explicite que
Ce est, les crochets autour des matrices sont remplacés par des barres verticales allongées.
Déterminants de matrices 2-en-2

La matrice 2 × 2
a déterminant
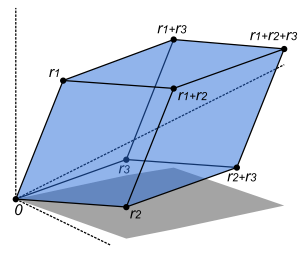
L'interprétation lorsque la matrice possède des entrées de nombre réel est que cela donne de la zone orientée du parallélogramme dont les sommets sont (0,0), (a, b), (a + c, b + d), et (c, d). La zone orientée est le même que l'habituel zone , sauf que ce est négatif lorsque les sommets sont répertoriés dans l'ordre dans le sens horaire.
L'hypothèse est que la transformation linéaire est appliquée à la ligne des vecteurs comme le produit matrice-vecteur 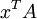 Où
Où  est un vecteur de colonne. Le parallélogramme sur la figure est obtenue en multipliant les vecteurs lignes
est un vecteur de colonne. Le parallélogramme sur la figure est obtenue en multipliant les vecteurs lignes  et
et 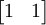 , Définissant les sommets du carré unité. Avec le produit matrice-vecteur plus fréquents
, Définissant les sommets du carré unité. Avec le produit matrice-vecteur plus fréquents 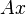 parallélogramme a sommets au
parallélogramme a sommets au 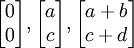 et
et  (Notez que
(Notez que 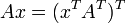 ).
).
Une formule pour les grandes matrices sera donnée ci-dessous.
Déterminants de matrices 3-par-3
La matrice 3 × 3:
En utilisant le l'expansion de cofacteur sur la première ligne de la matrice, on obtient:
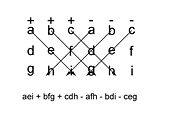
qui peut être dans les mémoires comme la somme des produits des trois diagonale nord-ouest des lignes sud-est d'éléments de la matrice, moins la somme des produits des trois diagonale sud-ouest vers les lignes nord-est d'éléments lorsque les exemplaires de la première deux colonnes de la matrice sont écrits à côté de lui comme ci-dessous:
Notez que cette mnémonique ne sont pas reportées dans les dimensions supérieures.
Applications
Déterminants sont utilisés pour caractériser matrices inversibles (ce est à dire, exactement ces matrices avec les déterminants non-zéro), et de décrire explicitement la solution à un système d' équations linéaires avec La règle de Cramer. Ils peuvent être utilisés pour trouver les valeurs propres de la matrice  à travers le polynôme caractéristique
à travers le polynôme caractéristique
où I est la matrice de même dimension que A d'identité.
On pense souvent que le déterminant l'attribution d'un numéro à chaque séquence de 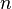 vecteurs de
vecteurs de 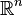 , En utilisant la matrice carrée dont les colonnes sont les vecteurs donnés. Grâce à cette compréhension, le signe du déterminant d'une base peut être utilisée pour définir la notion de orientation en espaces euclidiens . Le déterminant d'un ensemble de vecteurs est positif si les vecteurs forment un droitier système de coordonnées, et négative si-Gaucher.
, En utilisant la matrice carrée dont les colonnes sont les vecteurs donnés. Grâce à cette compréhension, le signe du déterminant d'une base peut être utilisée pour définir la notion de orientation en espaces euclidiens . Le déterminant d'un ensemble de vecteurs est positif si les vecteurs forment un droitier système de coordonnées, et négative si-Gaucher.
Les déterminants sont utilisées pour calculer les volumes de calcul vectoriel : la valeur absolue du déterminant de vecteurs réels est égal au volume de la parallélépipède engendré par ces vecteurs. En conséquence, si le linéaire 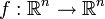 est représenté par la matrice
est représenté par la matrice  Et
Et 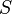 est tout mesurable sous-ensemble de
est tout mesurable sous-ensemble de 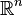 , Alors le volume de
, Alors le volume de 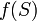 est donnée par
est donnée par 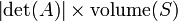 . Plus généralement, si la carte linéaire
. Plus généralement, si la carte linéaire 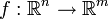 est représenté par la
est représenté par la  -by-
-by- 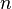 matrice
matrice  Et
Et 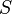 est tout sous-ensemble mesurable de
est tout sous-ensemble mesurable de 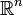 , Puis le
, Puis le 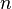 - volume tridimensionnel de
- volume tridimensionnel de 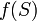 est donnée par
est donnée par 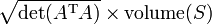 . En calculant le volume du tétraèdre délimitée par quatre points, ils peuvent être utilisés pour identifier lignes obliques.
. En calculant le volume du tétraèdre délimitée par quatre points, ils peuvent être utilisés pour identifier lignes obliques.
Le volume de ne importe quel tétraèdre , étant donné ses sommets a, b, c, et d, est (1/6) · | det (A - B, B - C, C - D) |, ou toute autre combinaison de paires de sommets qui forment un tout simplement connecté graphique.
Définition générale et de calcul
La définition du déterminant vient du théorème suivant.
Théorème. Soit M n (K) l'ensemble de tous 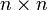 matrices sur le corps K. Il existe exactement une fonction
matrices sur le corps K. Il existe exactement une fonction
avec les deux propriétés:
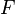 est alternatif multilinéaires en ce qui concerne les colonnes;
est alternatif multilinéaires en ce qui concerne les colonnes; 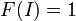 .
.
On peut alors définir le déterminant que la fonction unique avec les propriétés ci-dessus.
Pour prouver le théorème ci-dessus, on obtient aussi le Leibniz formule:
Voici la somme est calculée sur toutes les permutations 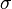 des nombres {1,2, ..., n} et
des nombres {1,2, ..., n} et 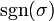 désigne le signature de la permutation
désigne le signature de la permutation 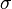 : 1 si
: 1 si 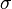 est un même permutation et -1 si elle est impair.
est un même permutation et -1 si elle est impair.
Cette formule contient 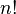 ( factorielle ) opérandes, et il est donc impossible de l'utiliser pour calculer les déterminants de grande
( factorielle ) opérandes, et il est donc impossible de l'utiliser pour calculer les déterminants de grande 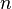 .
.
Pour les petites matrices, on obtient les formules suivantes:
- si
 est une matrice 1 par 1, puis
est une matrice 1 par 1, puis 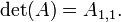
- si
 est une matrice deux par deux, puis
est une matrice deux par deux, puis 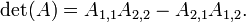
- pour une matrice 3 par 3
 La formule est plus complexe:
La formule est plus complexe:
qui prend la forme du régime de la Sarrus .
En général, les déterminants peuvent être calculées en utilisant l'élimination de Gauss utilisant les règles suivantes:
- Si
 est un matrice triangulaire, à savoir
est un matrice triangulaire, à savoir 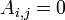 chaque fois que
chaque fois que 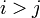 ou, alternativement, chaque fois
ou, alternativement, chaque fois 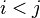 , Puis
, Puis 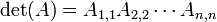 (Le produit des éléments diagonaux de
(Le produit des éléments diagonaux de  ).
). - Si
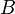 résultats de
résultats de  en échangeant deux rangées ou des colonnes, puis
en échangeant deux rangées ou des colonnes, puis 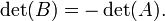
- Si
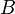 résultats de
résultats de  en multipliant une ligne ou une colonne avec le nombre
en multipliant une ligne ou une colonne avec le nombre  , Puis
, Puis 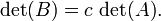
- Si
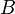 résultats de
résultats de  en ajoutant un multiple d'une colonne à une autre, ou à un multiple d'une colonne à une autre colonne, puis
en ajoutant un multiple d'une colonne à une autre, ou à un multiple d'une colonne à une autre colonne, puis 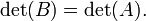
Explicitement, commencer avec une certaine matrice, utiliser les trois dernières règles pour le convertir en une matrice triangulaire, puis utiliser la première règle pour calculer son déterminant.
Il est également possible d'étendre un déterminant le long d'une rangée ou d'une colonne à l'aide La formule de Laplace, qui est efficace pour relativement petites matrices. Pour ce faire long d'une rangée  , Par exemple, nous écrivons
, Par exemple, nous écrivons
où le 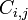 représenter la matrice des cofacteurs, à savoir
représenter la matrice des cofacteurs, à savoir 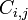 est
est 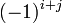 la fois mineur
la fois mineur 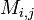 , Qui est le déterminant de la matrice qui en résulte
, Qui est le déterminant de la matrice qui en résulte  en enlevant le
en enlevant le 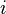 -ième rangée et de la
-ième rangée et de la 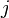 -ième colonne.
-ième colonne.
Exemple
Supposons que nous voulons calculer le déterminant de
Nous pouvons aller de l'avant et d'utiliser la formule de Leibniz directement:
Alternativement, nous pouvons utiliser La formule de Laplace pour élargir le déterminant le long d'une ligne ou une colonne. Il est préférable de choisir une ligne ou une colonne avec beaucoup de zéros, donc nous allons étendre le long de la deuxième colonne:
Une troisième voie (et la méthode de choix pour les grandes matrices) impliqueraient l'algorithme de Gauss. Quand vous faites des calculs à la main, on peut souvent réduire considérablement les choses en ajoutant intelligemment multiples de colonnes ou lignes à d'autres colonnes ou lignes; cela ne change pas la valeur du déterminant, mais peut créer des entrées de zéro, ce qui simplifie les calculs ultérieurs. Dans cet exemple, l'ajout de la deuxième colonne de la première est particulièrement utile:
et ce déterminant peut être rapidement étendu le long de la première colonne:
Propriétés
Le facteur multiplicatif est une carte en ce sens que
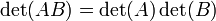 pour tout n -by- n matrices
pour tout n -by- n matrices  et
et 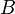 .
.
Ce est généralisée par la Formule de Cauchy-Binet aux produits de matrices non-carrés.
Il est facile de voir que 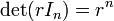 et ainsi
et ainsi
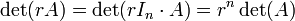 pour tous
pour tous 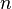 -by-
-by- 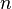 matrices
matrices  et tout scalaires
et tout scalaires  .
.
Une matrice sur un anneau commutatif R est inversible si et seulement si son déterminant est une unité dans R. En particulier, si A est une matrice au cours d'une domaine tel que les réels ou des nombres complexes , alors A est inversible si et seulement si det (A) ne est pas nul. Dans ce cas, nous avons
Exprimé différemment: les vecteurs v 1, ..., v n dans R n former un base si et seulement si det (v 1, ..., c n) est non nul.
Une matrice et son transposer le même déterminant:
Les déterminants d'une matrice complexe et de son conjugué transposer sont Conjugué:
(Notez le transposé conjugué est identique à la transposée d'une matrice réelle)
Le déterminant de la matrice  présente les propriétés suivantes sous des transformations de matrice élémentaire
présente les propriétés suivantes sous des transformations de matrice élémentaire  :
:
- Échanger des lignes ou des colonnes multiplie le déterminant par -1.
- Multipliant une rangée ou colonne par
 multiplie le facteur déterminant par
multiplie le facteur déterminant par  .
. - Ajout d'un multiple d'une ligne ou une colonne à l'autre laisse le déterminant inchangé.
Cela découle de la propriété multiplicatif et les déterminants de la élémentaires matrices de transformation de la matrice.
Si  et
et 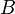 sont similaire, à savoir, se il existe une matrice inversible
sont similaire, à savoir, se il existe une matrice inversible 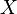 tel que
tel que  =
= 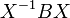 , Puis par la propriété multiplicatif,
, Puis par la propriété multiplicatif,
Cela signifie que le déterminant est un similitude invariant. Pour cette raison, le déterminant de certains transformation linéaire T: V → V pour certains de dimension finie espace vectoriel V est indépendant de la base de V. La relation est à sens unique, toutefois: il existe des matrices qui ont la même déterminant mais ne sont pas similaires.
Si  est un carré
est un carré 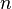 -by-
-by- 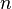 matrice avec réels ou complexes entrées et si λ 1, ..., λ n sont les (complexes) valeurs propres de
matrice avec réels ou complexes entrées et si λ 1, ..., λ n sont les (complexes) valeurs propres de  énumérés selon leurs multiplicités algébriques, puis
énumérés selon leurs multiplicités algébriques, puis
Cela découle du fait que  est toujours semblable à son Réduction de Jordan, une matrice triangulaire supérieure avec les valeurs propres sur la diagonale principale.
est toujours semblable à son Réduction de Jordan, une matrice triangulaire supérieure avec les valeurs propres sur la diagonale principale.
Identités utiles
Pour m -by- n matrice A et m -by- n matrice B, elle détient
Une conséquence de ces égalités pour le cas de (colonne) vecteurs x et y
Et une version généralisée de cette identité
Les preuves se trouvent dans .
matrices de bloc
Supposons, 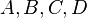 sont
sont 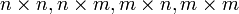 matrices, respectivement. Puis
matrices, respectivement. Puis
Cela peut être (assez) facilement visibles de l'exemple Formule de Leibniz. Employant l'identité suivante
mène à
Identité similaire avec 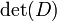 sur pondérée peut être dérivé analogue. Ces identités ont été prises à partir de .
sur pondérée peut être dérivé analogue. Ces identités ont été prises à partir de .
Si 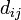 sont des matrices diagonales, puis
sont des matrices diagonales, puis
Ce est un cas particulier du théorème publié dans .
Relation avec trace
A partir de cette connexion entre le déterminant et les valeurs propres, on peut dériver une connexion entre le la fonction de trace, le fonction exponentielle, et le déterminant:
Effectuer la substitution 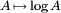 dans les rendements de l'équation ci-dessus
dans les rendements de l'équation ci-dessus
qui est étroitement liée à la Déterminant de Fredholm. De même,
Pour n -by- n matrices, il ya les relations:
- Cas n = 1:
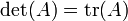
- Cas n = 2:
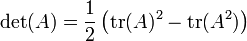
- Cas n = 3:
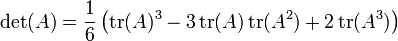
- Cas n = 4:
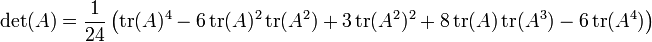
qui sont étroitement liés à Identités de Newton.
Dérivé
Le déterminant de véritables matrices carrées est une fonction polynomiale de 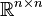 à
à 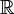 Et en tant que telle est partout différentiables . Son dérivé peut être exprimé en utilisant La formule de Jacobi:
Et en tant que telle est partout différentiables . Son dérivé peut être exprimé en utilisant La formule de Jacobi:
adj où (A) désigne le adjugate d'A. En particulier, si A est inversible, nous avons
Sous forme de composants, ce sont
Quand  est un petit nombre de ceux-ci sont équivalentes
est un petit nombre de ceux-ci sont équivalentes
Le cas particulier où  est égale à la matrice identité
est égale à la matrice identité 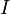 rendements
rendements
Une propriété utile dans le cas de matrices 3 x 3 est le suivant:
A peut être écrit comme 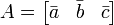 où
où 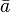 ,
, 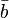 ,
, 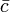 sont des vecteurs, le gradient sur l'une des trois vecteurs peut être écrit comme le produit croisé de deux autres:
sont des vecteurs, le gradient sur l'une des trois vecteurs peut être écrit comme le produit croisé de deux autres:
Résumé formulation
Un n × n matrice carrée A peut être considéré comme la représentation d'une coordonnée transformation linéaire d'un n de dimension espace vectoriel V. Compte tenu de toute transformation linéaire
nous pouvons définir le déterminant de A comme déterminant de toute représentation matricielle de A. C'est un notion bien définie (ce est à dire indépendant d'un choix de base) depuis le déterminant est invariant sous les transformations de similarité.
Comme on pouvait s'y attendre, il est possible de définir le déterminant d'une transformation linéaire de manière à coordonnées libre. Si V est un espace vectoriel de dimension n, alors on peut construire son sommet puissance extérieure Λ n V. Ce est un espace vectoriel unidimensionnel dont les éléments sont écrits
où chaque v i est un vecteur V et à la Produit en forme de coin est antisymétrique ∧ (c.-à-∧ u u = 0). Toute transformation linéaire A: V → V induit une transformation linéaire de Λ n V comme suit:
Depuis Λ n V est unidimensionnel cette opération est simplement multiplicative par un scalaire qui dépend d'un. Ce est ce qu'on appelle le scalaire déterminant de A. Autrement dit, on définit det (A) par l'équation
On peut vérifier que cette définition est d'accord avec la définition de coordonnées dépendante donnée ci-dessus.
Mise en œuvre algorithmique
- Procédé naïf de mettre en oeuvre un algorithme pour calculer le déterminant est d'utiliser la formule de Laplace pour l'expansion par cofacteurs. Cette approche est extrêmement inefficace en général, cependant, comme il est d'ordre n! (N factorielle ) pour une matrice n × n M.
- Une amélioration de l'ordre n 3 peut être réalisé en utilisant Décomposition LU écrire M = LU pour les matrices L et U triangulaire. Maintenant, det M = det LU = det L det U, et comme L et U sont triangulaires le déterminant de chacun est simplement le produit de ses éléments diagonaux. En variante, on peut effectuer la Décomposition de Cholesky, si possible, ou la QR décomposition et trouver le facteur déterminant d'une manière similaire.
- Depuis la définition du déterminant n'a pas besoin de divisions, une question se pose: faire des algorithmes rapides existantes qui ne ont pas besoin divisions? Ceci est particulièrement intéressant pour les matrices sur des anneaux. En effet avec des algorithmes d'exécution proportionnel à n 4 existent. Une algorithme de Mahajan et Vinay, et Berkowitz est basée sur promenades fermées commandés (court clow). Il calcule plus de produits que la définition déterminant exige, mais certains de ces produits annuler et la somme de ces produits peut être calculée de façon plus efficace. L'algorithme final ressemble beaucoup à un produit itérative des matrices triangulaires.
- Qu'est-ce ne est pas souvent discuté est la soi-disant «complexité de bits" du problème, ce est à dire le nombre de bits de précision dont vous avez besoin de stocker des valeurs intermédiaires. Par exemple, en utilisant l'élimination de Gauss , vous pouvez réduire la matrice à la forme triangulaire supérieure, puis multipliez la diagonale principale pour obtenir le déterminant (ce est essentiellement un cas particulier de la décomposition de LU comme ci-dessus), mais un calcul rapide montre que le bit taille de valeurs intermédiaires pourrait devenir exponentielle. On pourrait parler quand il est approprié d'arrondir les valeurs intermédiaires, mais une façon élégante de calculer le déterminant utilise le Bareiss algorithme, une méthode exacte répartition basée sur L'identité de Sylvester pour donner un moment de l'exécution de l'ordre n 3 et la complexité de bits à peu près la taille de bit des entrées originales dans les temps de la matrice n.
Histoire
Historiquement, les déterminants ont été pris en considération avant matrices. À l'origine, un facteur déterminant a été définie comme une propriété d'un système d'équations linéaires . Le déterminant «détermine», si le système a une solution unique (ce qui se produit avec précision si le déterminant est non nul). En ce sens, déterminants ont été utilisés d'abord dans le 3ème siècle avant JC chinoise mathématiques manuels Les Neuf Chapitres sur l'art mathématique. En Europe, deux par deux déterminants ont été examinées par Cardano à la fin de la 16ème siècle et les plus grands par Leibniz et, au Japon, par Seki environ 100 ans plus tard. Cramer (1750) ajouté à la théorie, le traitement du sujet par rapport à des ensembles d'équations. La loi récurrente a été annoncée par Bézout (1764).
C'était Vandermonde (1771) qui, le premier déterminants reconnu comme fonctions indépendantes. Laplace (1772) a donné la méthode générale de l'expansion d'un facteur déterminant en termes de sa complémentaire mineurs: Vandermonde avait déjà donné un cas particulier. Immédiatement après, Lagrange (1773) traités déterminants de la deuxième et de troisième ordre. Lagrange a été le premier à appliquer déterminants aux questions la théorie de l'élimination; il a prouvé bien des cas spéciaux d'identités générales.
Gauss (1801) fait la prochaine avance. Comme Lagrange, il a fait beaucoup d'utilisation de déterminants dans la théorie des nombres . Il a présenté les mots déterminants (Laplace avait utilisé résultante), mais pas dans le présent signification, mais plutôt comme appliquée à la un discriminant de quantique. Gauss est également arrivé à la notion de réciprocité (inverse) déterminants, et est venu très près le théorème de multiplication.
La prochaine contributeur est d'une importance Binet (1811, 1812), qui a officiellement déclaré le théorème concernant le produit de deux matrices de m colonnes et n lignes, qui, pour le cas particulier des m = n réduit au théorème de multiplication. Le même jour ( 30 novembre 1812 ) que Binet a présenté son document à l'Académie, Cauchy a également présenté une sur le sujet. (Voir Formule de Cauchy-Binet.) En cela, il a utilisé le mot déterminant dans son sens actuel, résumée et simplifiée ce qui était alors connu sur le sujet, a amélioré la notation, et a donné le théorème de multiplication avec une preuve plus satisfaisante que Binet. Avec lui commence la théorie dans sa généralité.
La prochaine figure importante était Jacobi (à partir de 1827). Il a utilisé tôt le déterminant fonctionnel qui Sylvester appelé plus tard Jacobienne, et dans ses mémoires en Crelle pour 1841, il traite spécialement ce sujet, ainsi que la classe de fonctions qui Sylvester a appelés alternants alternatif. Vers le temps de dernières mémoires de Jacobi, Sylvester (1839) et Cayley a commencé leur travail.
L'étude des formes spéciales de déterminants a été le résultat naturel de l'achèvement de la théorie générale. Déterminants axisymétriques ont été étudiés par Lebesgue, Hesse, et Sylvester; déterminants persymmetric par Sylvester et Hankel; circulants par Catalan, Spottiswoode, Glaisher, et Scott; déterminants et gauches Pfaffians, dans le cadre de la théorie de la transformation orthogonale, par Cayley; continuants par Sylvester; Wronskians (appelée ainsi par Muir) par Christoffel et Frobenius; composés déterminants par Sylvester, Reiss, et Picquet; Jacobiens et Hessois par Sylvester; et déterminants Gauche symétriques par Trudi. Des manuels sur le sujet de Spottiswoode était la première. En Amérique, Hanus (1886), Weld (1893), et Muir / Metzler (1933) publié traités.