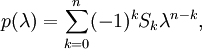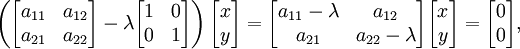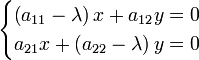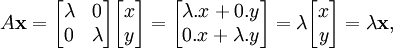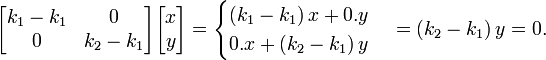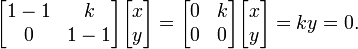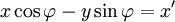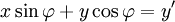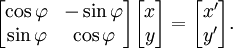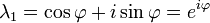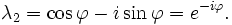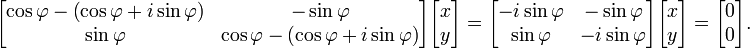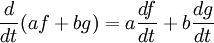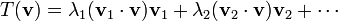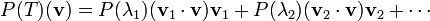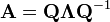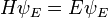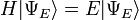Valeurs et vecteurs propres
Renseignements généraux
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Voir http://www.soschildren.org/sponsor-a-child pour connaître le parrainage d'enfants.

En mathématiques , un vecteur peut être considéré comme une flèche. Il a une longueur, appelé son ampleur, et il souligne dans une direction particulière. Un transformation linéaire peut être considéré pour fonctionner sur un vecteur pour le changer, en changeant souvent fois par son ampleur et sa direction. Un vecteur propre d'une transformation linéaire donnée est un vecteur qui est multiplié par une constante appelée valeurs propres au cours de cette transformation. La direction du vecteur propre est soit inchangée par cette transformation (par valeurs propres positives) ou inversée (pour valeurs propres négatives).
Par exemple, une valeur propre de 2 signifie que le vecteur propre est doublé en longueur et points dans la même direction. Une valeur propre de 1 signifie que le vecteur propre est inchangée, tandis qu'une valeur propre de -1 signifie que le vecteur propre est inversée dans la direction. Un espace propre d'une transformation donnée est la durée des vecteurs propres de cette transformation avec la même valeur propre, ainsi que le vecteur nul (ce qui n'a pas de direction). Un espace propre est un exemple d'un sous-espace d'un espace vectoriel .
En algèbre linéaire , chaque transformation linéaire entre les espaces vectoriels de dimension finie peut être donnée par une matrice , qui est un tableau rectangulaire de nombres disposés en rangées et en colonnes. Les méthodes standard pour trouver les valeurs propres, vecteurs propres et espaces propres d'une matrice donnée sont discutés ci-dessous.
Ces concepts jouent un rôle majeur dans plusieurs branches de fois pures et mathématiques appliquées - apparaissant en bonne place dans l'algèbre linéaire , analyse fonctionnelle, et dans une moindre mesure en mathématiques non linéaires.
De nombreux types d'objets mathématiques peuvent être traités comme des vecteurs: fonctions , modes harmoniques, états quantiques, et fréquences, par exemple. Dans ces cas, le concept de direction perd son sens ordinaire, et est donné une définition abstraite. Toutefois, si cette direction est inchangé abstraite par une transformation linéaire donné, le préfixe «eigen" est utilisé, comme dans fonction propre, mode propre, état propre et fréquence propre.
Histoire
Les valeurs propres sont souvent introduits dans le cadre de l'algèbre linéaire ou théorie de la matrice . Historiquement, cependant, ils ont été soulevées dans l'étude de formes et quadratique équations différentielles .
Euler avait également étudié le mouvement d'une rotation corps rigide et découvert l'importance de la axes principaux. Comme Lagrange réalisé, les axes principaux sont les vecteurs propres de la matrice d'inertie. Au début du 19e siècle, Cauchy a vu comment leur travail pourrait être utilisé pour classer le quadriques, et il généralisés aux dimensions arbitraires. Cauchy a aussi inventé la Caractéristique de racine terme (racine caractéristique) pour ce qui est maintenant appelé valeur propre; son mandat survit dans équation caractéristique.
Fourier utilisé le travail de Laplace et Lagrange pour résoudre le équation de la chaleur par séparation des variables dans son célèbre livre 1822 Théorie analytique de la chaleur. Sturm a développé les idées de Fourier plus loin et il les conduisit à l'attention de Cauchy, qui les combine avec ses propres idées et il est arrivé par le fait que les matrices symétriques ont de vraies valeurs propres. Cela a été prolongée par Hermite en 1855 à ce que l'on appelle aujourd'hui Matrices hermitiennes. Vers la même époque, Brioschi prouvé que les valeurs propres de matrices orthogonales se trouvent sur le cercle unité, et Clebsch trouvé le résultat correspondant pour antisymétriques matrices. Finalement, Weierstrass clarifié un aspect important dans la théorie de la stabilité commencé par Laplace en réalisant que matrices défectueux peuvent provoquer une instabilité.
Pendant ce temps, Liouville a étudié les problèmes de valeurs propres similaires à celles de Sturm; la discipline qui est née de leur travail est maintenant appelé Théorie de Sturm-Liouville. Schwarz a étudié la première valeur propre de L'équation de Laplace sur les domaines généraux vers la fin du 19ème siècle, tandis que Poincaré a étudié L'équation de Poisson quelques années plus tard.
Au début du 20e siècle, Hilbert a étudié les valeurs propres de opérateurs intégraux en consultant les opérateurs comme matrices infinies. Il était le premier à utiliser le allemand eigen mot pour désigner valeurs et vecteurs propres en 1904, mais il a peut-être été la suite d'une utilisation liée par Helmholtz. "Eigen" peut être traduit comme "propre", "propre à", "caractéristique" ou "individuelle" -emphasizing l'importance de valeurs propres sont de définir la nature unique d'une transformation spécifique. Depuis quelque temps, le terme standard en anglais était "valeur adéquate", mais le terme le plus distinctif "valeur propre" est aujourd'hui la norme.
Le premier algorithme numérique pour calculer les valeurs propres et les vecteurs propres est apparu en 1929, lorsque Von Mises a publié le Procédé d'alimentation. Une des méthodes les plus populaires aujourd'hui, le Algorithme QR, a été proposé indépendamment par Francis et Kublanovskaya en 1961.
Définitions: l'équation aux valeurs propres
Transformations linéaires d'un espace vectoriel, tels que rotation, réflexion, étirage, compression, cisaillement ou une combinaison de ceux-ci, peuvent être visualisées par l'effet qu'ils produisent sur des vecteurs . En d'autres termes, ce sont des fonctions vectorielles. Plus formellement, dans un espace vectoriel L une fonction vecteur A est défini si, pour chaque vecteur x de L correspond un vecteur unique, y = A (x) de L. Par souci de concision, les parenthèses autour du vecteur sur lequel la transformation est intérim sont souvent omis. Une fonction de vecteur A est linéaire si elle a les deux propriétés suivantes:
- additivité
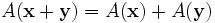
- homogénéité
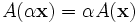
où x et y sont tous deux des vecteurs de l'espace vectoriel et α L est ne importe quel nombre réel . Une telle fonction est diversement appelé une transformation linéaire, opérateur linéaire, ou linéaire endomorphisme sur l'espace L.
Compte tenu d'une transformation linéaire A, un vecteur non nul x est défini comme étant un vecteur propre de la transformation se il satisfait à l'équation de valeur propre λ = A x x pour une λ scalaire. Dans cette situation, le scalaire λ est appelé une valeur propre de A correspondant au vecteur propre x. |
L'équation clé dans cette définition est l'équation aux valeurs propres, A x = λ x. La plupart des vecteurs x ne seront pas satisfaire une telle équation. Un vecteur typique x change de direction lorsque sollicité par un, de sorte que A x ne est pas un multiple de x. Cela signifie que seulement certains vecteurs sont des vecteurs propres spécifiques x, et seuls certains numéros spéciaux sont les valeurs propres λ. Bien sûr, si A est un multiple de la matrice d'identité, alors aucun vecteur change de direction et tous les vecteurs non nuls sont des vecteurs propres. Mais dans le cas d'habitude, vecteurs propres sont rares et espacées. Ce sont les "modes normaux» du système, et ils agissent de façon indépendante.
L'exigence que le vecteur propre non nulle est imposée parce que l'équation A 0 = λ 0 détient pour chaque A et chaque λ. Depuis l'équation est toujours trivialement vrai, ce ne est pas un cas intéressant. En revanche, une valeur propre peut être égal à zéro de manière non triviale. Une valeur propre peut être, et est généralement, également un nombre complexe . Dans la définition donnée ci-dessus, les vecteurs propres et les valeurs propres ne se produisent pas de façon indépendante. Au lieu de cela, chaque vecteur propre est associé à une valeur propre spécifique. Pour cette raison, et x un vecteur propre d'une valeur propre λ correspondant sont souvent désignés en tant que eigenpair. Une valeur propre peut être associé à plusieurs ou même avec un nombre infini de vecteurs propres. Mais à l'inverse, si un vecteur propre est donné, la valeur propre associée à ce vecteur propre est unique. En effet, de l'égalité A x = λ x = λ 'x et de x ≠ 0, il se ensuit que λ = λ.

Géométriquement (Fig. 2), l'équation de valeur propre signifie que, dans la transformation des vecteurs propres d'une expérience seulement des changements dans amplitude et le signe - la direction de A x est la même que celle de x. Ce type de transformation linéaire est défini comme étant homothétie (dilatation, la transformation similitude). La valeur propre λ est simplement la quantité de «étirer» ou «psy» à laquelle un vecteur est soumis lorsqu'il est transformé par A. Si λ = 1, le vecteur reste inchangé (affecté par la transformation). Une transformation I dans laquelle un vecteur x reste inchangé, I x = x, est définie comme transformation d'identité. Si λ = -1, le vecteur retourne dans la direction opposée (tourne à 180 °); ce est définie comme réflexion.
Si x est un vecteur propre de la transformation linéaire A avec λ valeur propre, alors tout vecteur y = α x est aussi un vecteur propre de A avec la même valeur propre. De l'homogénéité de la transformation A il en résulte que α = A y (A x) = α (λ x) = λ (α x) = λ y. De même, en utilisant la propriété d'additivité de la transformation linéaire, il peut être démontré que toute combinaison linéaire des vecteurs propres de valeur propre λ a la même valeur propre λ. Par conséquent, tout vecteur non-zéro dans la ligne passant par x et le vecteur nul est un vecteur propre avec la même valeur propre que x. Avec le vecteur nul, ces vecteurs propres forment un sous-espace de l'espace vectoriel appelé un espace propre. Les vecteurs propres correspondant à différentes valeurs propres sont linéairement sens indépendante, en particulier, que dans un espace de dimension n la transformation linéaire A ne peut pas avoir plus de n vecteurs propres avec différentes valeurs propres. Les vecteurs de l'espace propre de générer un sous-espace linéaire de A qui est invariant (inchangé) en vertu de cette transformation.
Si un base est défini dans l'espace vectoriel L n, tous les vecteurs peuvent être exprimées en termes de composants . Vecteurs polaires peuvent être représentés comme une matrice-colonne à n lignes, où n est le nombre de dimensions de l'espace. Transformations linéaires peuvent être représentés avec des matrices carrées; à chaque transformation linéaire A de L n correspond une matrice carrée de rang n. Inversement, à chaque matrice carrée de rang n correspond une transformation linéaire de L n à une base donnée. En raison de l'additivité et l'homogénéité du trasformation linéaire et l'équation aux valeurs propres (qui est aussi une transformation linéaire - homothétie), ces fonctions vectorielles peuvent être exprimées sous forme de matrice. Ainsi, dans l'un vecteur bidimensionnel espace L 2 équipé base standard, l'équation de vecteur propre pour une transformation linéaire A peut être écrit dans la représentation matricielle suivante:
où la juxtaposition des matrices signifie la multiplication de matrices . Ceci est équivalent à un ensemble de n équations linéaires, où n est le nombre de vecteurs de base de la base indiquée. Dans ces équations à la fois la valeur propre λ de et les composantes de x sont inconnues Variables.
Les vecteurs propres de A tels que définis ci-dessus sont également appelés vecteurs propres à droite parce qu'ils sont des vecteurs colonnes qui se dressent sur le côté droit de la matrice A dans l'équation aux valeurs propres. Se il existe une matrice transposée A T Statisfait que l'équation de valeur propre, qui est, si A = T x λ x, alors x T = λ (λ x) = T (A T x) = x T T A, T ou X A = λ x T. La dernière équation est similaire à l'équation aux valeurs propres mais au lieu de le vecteur colonne x il contient son vecteur transposé, le vecteur ligne x T, qui se dresse sur le côté gauche de la matrice A. Les vecteurs propres qui satisfont l'équation x valeur propre T A = λ x T sont appelés vecteurs propres gauches. Ils sont des vecteurs de rangée. Dans de nombreuses applications communes, seuls vecteurs propres à droite doivent être considérés. D'où le terme absolu "vecteur propre» peut être compris comme se référant à un vecteur propre droit. Équations aux valeurs propres, écrites en termes de vecteurs propres à droite ou à gauche (A x = λ x et x T x A = λ T) ont la même valeur propre λ.
Un vecteur propre est défini comme étant un principal ou vecteur propre dominante si elle correspond à la valeur propre de plus grande amplitude (pour nombres réels, la plus grande valeur absolue). L'application répétée d'une transformation linéaire pour un résultat de vecteurs arbitraires dans un vecteur proportionnel (colinéaires) au vecteur propre capital.
L'applicabilité l'équation de valeur propre à la théorie de la matrice générale étend l'utilisation de vecteurs et valeurs propres à toutes les matrices, et donc grandement étend le champ d'utilisation de ces constructions mathématiques non seulement à des transformations dans les espaces vectoriels linéaires mais à tous les domaines de la science qui utilisent des matrices: équations linéaires systèmes, optimisation, vecteur et calcul tensoriel, tous les domaines de la physique qui utilisent des quantités de matrice, la physique quantique, la relativité en particulier, et de l'électrodynamique, ainsi que de nombreuses applications d'ingénierie.
Équation caractéristique
La détermination des valeurs et vecteurs propres est important dans pratiquement tous les domaines de la physique et de nombreux problèmes d'ingénierie, comme des calculs de stress, analyse de la stabilité, des oscillations des systèmes vibrants, etc. Il est équivalent à diagonalisation des matrices, et est la première étape d'orthogonalisation, trouver des invariants, l'optimisation (minimisation ou la maximisation), l'analyse des systèmes linéaires, et de nombreuses autres applications courantes.
La méthode habituelle de trouver tous les vecteurs et valeurs propres d'un système est le premier à se débarrasser des éléments inconnus des vecteurs propres, puis de trouver les valeurs propres, branchez ceux qui reviennent un par un dans l'équation aux valeurs propres sous forme de matrice et résoudre ce comme un système de équations linéaires pour trouver les composantes des vecteurs propres. De la transformation d'identité I x = x, où I est la matrice d'identité, x dans l'équation de valeur propre peut être remplacée par I x à envoyer:
La matrice d'identité est nécessaire pour maintenir les matrices, vecteurs et scalaires droite; l'équation (A - λ) x = 0 est plus courte, mais mélangé car il ne fait pas de distinction entre la matrice, scalaire et vectoriel. L'expression dans le côté droit est transféré vers le côté gauche avec un signe négatif, laissant 0 sur le côté droit:
Le vecteur propre x est tiré derrière parenthèses:
Cela peut être considéré comme un système d'équations linéaires dans lequel la matrice de coefficients est l'expression entre parenthèses, la matrice des inconnues est x, et la matrice de droite est nul. Selon La règle de Cramer, ce système d'équations a des solutions non triviales (pas tous des zéros, ou pas de nombre) si et seulement si son déterminant disparaît, de sorte que les solutions de l'équation sont donnés par:
Cette équation est définie comme la équation caractéristique (moins souvent, équation séculaire) de A, et le côté gauche est définie comme la polynôme caractéristique. Le vecteur propre x ou de ses composants ne sont pas présents dans l'équation caractéristique, de sorte à ce stade, ils sont supprimés, et les seules inconnues qui restent à être calculé sont les valeurs propres (les composants de la matrice A sont donnés, i. E, su à l'avance ). Pour un espace vectoriel L 2, la transformation A est une matrice carrée 2 × 2, et l'équation caractéristique peut être écrit sous la forme suivante:
Expansion du déterminant dans les résultats de côté gauche dans un polynôme caractéristique qui est un Monic (son coefficient de premier plan est une) polynomiale de la seconde degré, et l'équation caractéristique est la équation quadratique
qui a les solutions suivantes ( racines):
Pour les matrices réelles, les coefficients du polynôme caractéristique sont toutes réelles. Le nombre et le type des racines dépend de la valeur de la discriminante, D. Pour les cas D = 0, D> 0, ou D <0, respectivement, les racines sont une réalité, deux réel, deux ou complexe. Si les racines sont complexes, ils sont aussi complexes conjugués de l'autre. Lorsque le nombre de racines est inférieur au degré du polynôme caractéristique (ce dernier est aussi le rang de la matrice, et le nombre de dimensions de l'espace vectoriel) l'équation a une racine multiple. Dans le cas d'une équation quadratique avec une racine, cette racine est une racine double, ou avec une racine 2. Une multiplicité racine avec une multiplicité de 1 est une racine simple. Une équation quadratique avec deux racines réelles ou complexes a des racines simples. En général, la algébrique multiplicité d'une valeur propre est définie comme la multiplicité correspondante de la racine du polynôme caractéristique. Le spectre d'une transformation sur une dimension finie espace vectoriel est défini comme le ensemble de toutes ses valeurs propres. Dans le cas de dimension infinie, le concept de spectre est plus subtile et dépend de la topologie de l'espace vectoriel.
La formule générale pour le polynôme caractéristique d'une matrice de n est -carré
où S 0 = 1, S 1 = tr (A), le trace de la matrice de transformation A, et S k avec k> 1 sont les sommes du principal mineurs d'ordre k. Le fait que les valeurs propres sont racines d'une équation n -condamner montre qu'une transformation linéaire d'un espace linéaire de dimension n a au plus n valeurs propres différentes. Selon le théorème fondamental de l'algèbre, dans un espace linéaire complexe, le polynôme caractéristique a au moins un zéro. Par conséquent, toute transformation linéaire d'un espace linéaire complexe comporte au moins une valeur propre. Pour les espaces linéaires réels, si la dimension est un nombre impair, la transformation linéaire a au moins une valeur propre; si la dimension est un nombre pair, le nombre de valeurs propres dépend du déterminant de la matrice de transformation: si le déterminant est négatif, il existe au moins l'une positive et une valeur propre négative, si le déterminant ne est rien positive peut être dit à propos de l'existence de valeurs propres. La complexité du problème de trouver des racines / valeurs propres de la caractéristique augmente rapidement avec l'augmentation du polynôme du degré du polynôme (la dimension de l'espace vectoriel), n. Ainsi, pour n = 3, les valeurs propres sont des racines de la équation cubique, pour n = 4 - racines de la équation quartique. Pour n> 4, il n'y a pas de solutions exactes et il faut recourir à des algorithmes de profondes enquête, comme la méthode de Newton ( La méthode de Horner) pour trouver des approximations numériques de valeurs propres. Pour les grandes symétrique matrices creuses, Lanczos algorithme est utilisé pour calculer des valeurs propres et des vecteurs propres.
Afin de trouver les vecteurs propres, les valeurs propres ainsi trouvés que les racines des équations caractéristiques sont branchés en arrière, un à la fois, dans l'équation aux valeurs propres écrite dans une forme de matrice (illustrés pour le cas le plus simple d'un à deux dimensions espace vectoriel L 2 ):
où λ est l'une des valeurs propres trouvées comme une racine de l'équation caractéristique. Cette équation matricielle est équivalent à un système de deux équations linéaires:
Les équations sont résolues pour x et y par les méthodes algébriques ou matrice habituels. Souvent, il est possible de diviser les deux côtés des équations à une ou plusieurs des coefficients qui rend certains des coefficients devant les inconnues égal à 1. Ceci est appelé normalisation des vecteurs, et correspond à choisir l'un des vecteurs propres (le vecteur propre normalisé) comme représentatif de tous les vecteurs dans l'espace propre correspondant à la valeur propre respective. X et Y sont ainsi trouvé les composantes du vecteur propre dans le système de coordonnées utilisé (le plus souvent cartésien ou polaire).
En utilisant le Cayley-Hamilton théorème qui stipule que chaque matrice carrée satisfait sa propre équation caractéristique, il peut être démontré que (le plus généralement, dans l'espace complexe), il existe au moins un vecteur non nul qui satisfait l'équation aux valeurs propres à cette matrice. Comme il a été dit dans la section Définitions, à chaque valeur propre correspond un nombre infini de colinéaires vecteurs propres (linéairement dépendants) qui forment l'espace propre pour cette valeur propre. D'autre part, la dimension de l'espace propre est égal au nombre de vecteurs propres linéairement indépendants qu'il contient. La multiplicité géométrique d'une valeur propre est définie comme la dimension de l'espace propre associé. Une valeur propre multiple peut donner lieu à un seul vecteur propre de telle sorte que sa multiplicité algébrique peut être différente de la multiplicité géométrique. Cependant, comme déjà dit, les différentes valeurs propres sont appariés avec les vecteurs propres linéairement indépendants. De ce qui précède, il résulte que la multiplicité géométrique ne peut pas être supérieure à la multiplicité algébrique.
Par exemple, un vecteur propre d'une rotation en trois dimensions est un vecteur situé dans la l'axe autour duquel se effectue la rotation. La valeur propre correspondante est 1 et l'espace propre correspondant contient tous les vecteurs long de l'axe. Comme il se agit d'un espace à une dimension, sa multiplicité géométrique est une. Ce est la seule valeur propre du spectre (de cette rotation) qui est un nombre réel .
Exemples
Les exemples qui suivent sont pour le cas le plus simple de vecteur à deux dimensions espace L 2 mais ils peuvent facilement être appliquées de la même manière à des espaces de dimensions supérieures.
Homothétie, l'identité, le point de réflexion et de transformation nulle
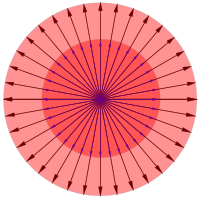
En unidimensionnel espace vectoriel L 1, envisager une chaîne de caoutchouc lié au soutien immobile dans une extrémité, comme celle sur la fronde d'un enfant. Tirer la corde loin du point d'attache se étend et se allonge par un facteur d'échelle λ qui est un nombre réel. Chaque vecteur de la corde est tendue de façon égale, avec le même facteur d'échelle λ, et même si elle conserve allongé sa direction d'origine. Ce type de transformation est appelé homothétie (transformation de similitude). Pour un espace vectoriel à deux dimensions L 2, envisager une feuille de caoutchouc étiré dans toutes les directions comme une petite zone de la surface d'un ballon à gonfler (Fig. 3). Tous les vecteurs qui proviennent d'un point fixe sur la surface du ballon sont étirées aussi avec le même facteur d'échelle λ. La transformation de homothétie en deux dimensions est décrit par une matrice carrée 2 × 2, agissant sur un vecteur arbitraire dans le plan de la / surface rétrécissement étirement. Après avoir fait la multiplication de la matrice, on obtient:
qui, exprimée en termes, signifie que la transformation est équivalent à la multiplication de la longueur du vecteur par λ tout en conservant son orientation d'origine. L'équation ainsi obtenue est exactement l'équation aux valeurs propres. Depuis le vecteur prise était arbitraire, dans toute homothétie vecteur dans l'espace vectoriel subit l'équation aux valeurs propres, ce est à dire tout vecteur couché sur la surface du ballon peut être un vecteur propre. Si la transformation est l'étirement (élongation, l'extension, l'inflation), ou de rétrécissement (compression, la déflation) dépend du facteur d'échelle: si λ> 1, il se étire, si λ <1, il se rétrécit.
Plusieurs autres transformations peuvent être considérées comme des types spéciaux de homothétie de certains, valeur constante fixe de λ: dans l'identité qui laisse inchangée vecteurs, λ = 1; en réflexion autour d'un point qui préserve la longueur et la direction des vecteurs mais modifie leur orientation opposée à celle, λ = -1; et en transformation nulle qui transforme chaque vecteur au vecteur nul, λ = 0. La transformation nulle ne donne pas lieu à un vecteur propre étant donné que le vecteur nul ne peut être un vecteur propre mais il a depuis espace propre espace propre contient aussi le vecteur nul par définition.
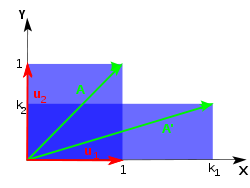
Mise à l'échelle inégale
Pour un exemple un peu plus compliqué, envisager une feuille qui est étiré uneqally dans deux directions perpendiculaires le long des axes de coordonnées, ou, de même, étiré dans une direction, et diminué dans l'autre sens. Dans ce cas, il existe deux facteurs d'échelle différents: k 1, pour la mise à l'échelle dans la direction x et k 2 pour la mise à l'échelle dans la direction y. La matrice de transformation est 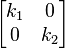 Et l'équation caractéristique est λ 2 - λ (k 1 + k 2) + k 1 k 2 = 0. Les valeurs propres, obtenu comme racines de cette équation sont λ 1 = k 1 et λ 2 = k 2 signifie, comme prévu, que les deux valeurs propres sont les facteurs d'échelle dans les deux directions. Branchement k 1 retour dans l'équation donne une valeur propre des vecteurs propres:
Et l'équation caractéristique est λ 2 - λ (k 1 + k 2) + k 1 k 2 = 0. Les valeurs propres, obtenu comme racines de cette équation sont λ 1 = k 1 et λ 2 = k 2 signifie, comme prévu, que les deux valeurs propres sont les facteurs d'échelle dans les deux directions. Branchement k 1 retour dans l'équation donne une valeur propre des vecteurs propres:
En divisant par la dernière équation k 2 - k 1, on obtient y = 0, qui représente l'axe x. Un vecteur de longueur 1 prise le long de cet axe représente le vecteur propre normalisé correspondant à la valeur propre λ 1. Le vecteur propre correspondant à λ 2 qui est un vecteur unitaire le long de l'axe des y se trouve d'une manière similaire. Dans ce cas, les deux valeurs propres sont simples (avec algébrique et multiplicités géométriques égal à 1). Selon les valeurs de λ 1 et λ 2, il existe plusieurs cas particuliers notables. En particulier, si λ 1> 1 et λ 2 = 1, la transformation est un étirement dans la direction de l'axe x. Si λ 2 = 0, 1 et λ = 1, la transformation est une projection de la surface L 2 sur l'axe x, car tous les vecteurs dans la direction de y deviennent vecteurs nuls.
Que la feuille de caoutchouc est tendue le long de l'axe x (k 1> 1) et simultanément rétréci le long de l'axe y (k 2 <1) comme sur la Fig. 4. Puis λ = 1 k 1 aura la valeur propre principale. Application répétée cette transformation d'étirement / contraction de nombreuses fois à la feuille de caoutchouc tournera ce dernier de plus en plus semblable à une chaîne de caoutchouc. Tout vecteur sur la surface de la feuille de caoutchouc sera orienté de proche en proche à la direction de l'axe x (la direction d'étirage), ce est-il deviendra colinéaire avec le vecteur propre principale.
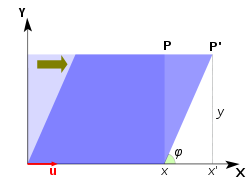
Cisaille
Dans le plan de cisaillement est une transformation dans laquelle tous les points le long d'une ligne donnée restent fixes alors que les autres points sont décalés parallèlement à cette ligne d'une distance proportionnelle à leur distance perpendiculaire de la ligne. Contrairement échelle, cisaillement une figure plane ne change pas son domaine. Cisaillement peut être horizontale - le long de l'axe X, ou vertical - le long de l'axe Y. Dans cisaillement horizontal (Fig. 5), un point P de l'avion se déplace parallèlement à l'axe X à l'endroit P 'de sorte que sa coordonnée Y ne change pas alors que le x incréments pour devenir coordonnée x' = x + k, où k est appelé facteur de cisaillement. Le facteur de cisaillement est proportionnelle à y et à l'angle φ cisaillement: k = x '- x = y φ de lit bébé. La matrice d'une transformation de cisaillement horizontal est 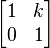 . L'équation caractéristique est λ 2 - 2 λ + 1 = (1 - λ) 2 = 0, qui a une seule racine λ = 1. Par conséquent, la valeur propre λ = 1 est multiple avec multiplicité algébrique 2. Le vecteur propre (s) se trouvent sous forme de solutions de
. L'équation caractéristique est λ 2 - 2 λ + 1 = (1 - λ) 2 = 0, qui a une seule racine λ = 1. Par conséquent, la valeur propre λ = 1 est multiple avec multiplicité algébrique 2. Le vecteur propre (s) se trouvent sous forme de solutions de
La dernière équation est divisé par k (normalisation) pour obtenir y = 0, qui est une ligne droite le long de l'axe x. Cette ligne représente l'espace propre à une dimension. Dans le cas d'un cisaillement de la multiplicité algébrique de la valeur propre (2) est inférieure à sa multiplicité géométrique (1, la dimension de l'espace propre). Le vecteur propre est un vecteur unitaire le long de l'axe x. Le cas de cisaillement vertical avec matrice de transformation 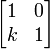 est traitée de la même façon; le vecteur propre au cisaillement vertical est le long de l'axe y. L'application de la transformation à plusieurs reprises cisaillement change la direction de ne importe quel vecteur dans le plan de proche en proche à la direction du vecteur propre.
est traitée de la même façon; le vecteur propre au cisaillement vertical est le long de l'axe y. L'application de la transformation à plusieurs reprises cisaillement change la direction de ne importe quel vecteur dans le plan de proche en proche à la direction du vecteur propre.
Rotation
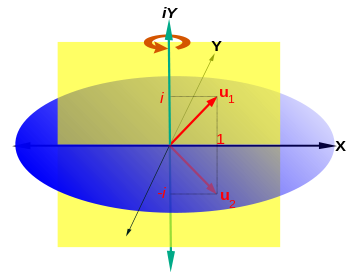
Un rotation dans un plan est une transformation qui décrit le mouvement d'un corps rigide (ou vecteur) autour d'un point fixe. Avec l'aide de fonctions trigonométriques, la rotation peut être décrite comme une transformation linéaire. Les éléments d'une matrice de rotation représentent les composantes du vecteur rotation. Ainsi, un sens inverse des aiguilles d'une rotation de coordonnées, un vecteur ou plan sur l'origine d'un angle φ de sorte que les coordonnées x et y de changement x 'et y' sont décrits par le système d'équations linéaires suivant:
ou, en termes de matrices et des vecteurs de colonnes:
L'équation caractéristique de la matrice de transformation 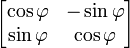 est λ 2 - 2λ cos φ + 1 = 0. Cette équation quadratique a un discriminant D = 4 (2 cos φ - 1) = - 4 sin 2 φ qui est un nombre négatif pour φ ≠ 0 ° et 180 ° φ ≠ × k avec k impair. Par conséquent, sauf pour ces derniers cas spéciaux, racines réelles (valeurs propres) ne existent pas pour la rotation. L'équation caractéristique a deux racines complexes λ 1 et λ 2, qui sont des conjugués complexes de l'autre:
est λ 2 - 2λ cos φ + 1 = 0. Cette équation quadratique a un discriminant D = 4 (2 cos φ - 1) = - 4 sin 2 φ qui est un nombre négatif pour φ ≠ 0 ° et 180 ° φ ≠ × k avec k impair. Par conséquent, sauf pour ces derniers cas spéciaux, racines réelles (valeurs propres) ne existent pas pour la rotation. L'équation caractéristique a deux racines complexes λ 1 et λ 2, qui sont des conjugués complexes de l'autre:
Ces deux racines sont les deux valeurs propres de rotation chacune avec une multiplicité algébrique égal à 1. Brancher la première valeur propre, λ 1, de retour dans l'équation aux valeurs propres donne le premier vecteur propre:
D'autres exemples
Comme la Terre tourne, chaque flèche pointant vers l'extérieur depuis le centre de la Terre tourne également, à l'exception des flèches qui sont parallèles à l'axe de rotation. Considérez la transformation de la Terre après une heure de rotation: Une flèche du centre de la Terre à la Geographic Pôle Sud serait un vecteur propre de cette transformation, mais une flèche du centre de la Terre à n'importe où sur le équateur ne serait pas un vecteur propre. Depuis la flèche pointant vers le pôle est pas étirée par la rotation de la Terre, sa valeur propre est 1.

Cependant, l'espace géométrique tridimensionnel est pas le seul espace vectoriel. Par exemple, considérons une corde souligné fixe aux deux extrémités, comme les cordes vibrantes d'un instrument à cordes (Fig. 2). Les distances des atomes de la corde vibrante à partir de leurs positions lorsque la corde est au repos peuvent être considérées comme les composantes d'un vecteur dans un espace à autant de dimensions qu'il ya atomes dans le câble.
Supposons que la corde est un milieu continu. Si l'on considère l'équation pour l' accélération à chaque point de la corde, ses vecteurs propres, ou de fonctions propres , sont les ondes stationnaires. Les ondes stationnaires correspondent à des oscillations particulières de la corde de telle sorte que l'accélération de la corde est tout simplement sa forme réduite par un facteur de ce facteur, la valeur propre, se révèle être 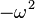 où
où 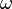 est le la fréquence angulaire de l'oscillation. Chaque composante du vecteur associé à la corde est multiplié par un facteur dépendant du temps
est le la fréquence angulaire de l'oscillation. Chaque composante du vecteur associé à la corde est multiplié par un facteur dépendant du temps 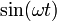 . Si d'amortissement est considéré, la amplitude de cette oscillation diminue jusqu'à ce que la corde arrête oscillant, ce qui correspond à un complexe ω. On peut alors associer une vie avec la partie imaginaire de ω, et concernent le concept d'un vecteur propre à la notion de résonance. sans amortissement, le fait que l'opérateur d'accélération (en supposant une densité uniforme) est conduit hermitiques à plusieurs propriétés importantes, comme celle les modèles de vagues permanentes sont des fonctions orthogonales.
. Si d'amortissement est considéré, la amplitude de cette oscillation diminue jusqu'à ce que la corde arrête oscillant, ce qui correspond à un complexe ω. On peut alors associer une vie avec la partie imaginaire de ω, et concernent le concept d'un vecteur propre à la notion de résonance. sans amortissement, le fait que l'opérateur d'accélération (en supposant une densité uniforme) est conduit hermitiques à plusieurs propriétés importantes, comme celle les modèles de vagues permanentes sont des fonctions orthogonales.
Fonctions propres
Cependant, il est parfois contre nature, voire impossible d'écrire l'équation aux valeurs propres dans une forme de matrice. Cela se produit par exemple lorsque l'espace vectoriel de dimension infinie est, par exemple, dans le cas de la corde au-dessus. Selon la nature de la transformation T et l'espace à laquelle il est applicable, il peut être avantageux pour représenter l'équation de valeur propre comme un ensemble d' équations différentielles . Si T est un opérateur différentiel, les vecteurs propres sont communément appelés fonctions propres de l'opérateur différentiel représentant T . Par exemple, différenciation lui-même est une transformation linéaire depuis
(f(t) etg(t) sont desfonctions différentiables, etunetbsont desconstantes).
Envisager la différenciation par rapport à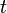 .ses fonctions propresh(t) obéir à l'équation aux valeurs propres:
.ses fonctions propresh(t) obéir à l'équation aux valeurs propres:
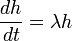 ,
,
où λ est la valeur propre associée à la fonction. Une telle fonction du temps est constant si 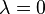 , croît proportionnellement à lui-même si
, croît proportionnellement à lui-même si 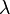 est positif, et se désintègre proportionnellement à lui-même si
est positif, et se désintègre proportionnellement à lui-même si 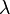 est négatif. Par exemple, une population de lapins idéalisée se reproduit autant plus vite que les lapins, il ya, et donc satisfait à l'équation avec un lambda positif.
est négatif. Par exemple, une population de lapins idéalisée se reproduit autant plus vite que les lapins, il ya, et donc satisfait à l'équation avec un lambda positif.
La solution de l'équation de valeur propre est 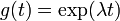 , la fonction exponentielle ; ainsi que la fonction est une fonction propre de l'opérateur différentiel d / dt à la valeur propre λ . Si λ est négative , nous appelons l'évolution de g un de décroissance exponentielle; si il est positif , une croissance exponentielle . La valeur de λ peut être tout nombre complexe . Le spectre de d / dt est par conséquent tout le plan complexe . Dans cet exemple, l'espace de vecteur dans lequel l'opérateur d / dt agit est l'espace des fonctions différentiables d'une variable. Cet espace a une dimension infinie (car il est impossible d'exprimer toute fonction différentiable comme une combinaison linéaire d'un nombre fini de fonctions de base). Cependant, l'espace propre associé à une valeur propre donnée λ est unidimensionnel. Il est l'ensemble de toutes les fonctions
, la fonction exponentielle ; ainsi que la fonction est une fonction propre de l'opérateur différentiel d / dt à la valeur propre λ . Si λ est négative , nous appelons l'évolution de g un de décroissance exponentielle; si il est positif , une croissance exponentielle . La valeur de λ peut être tout nombre complexe . Le spectre de d / dt est par conséquent tout le plan complexe . Dans cet exemple, l'espace de vecteur dans lequel l'opérateur d / dt agit est l'espace des fonctions différentiables d'une variable. Cet espace a une dimension infinie (car il est impossible d'exprimer toute fonction différentiable comme une combinaison linéaire d'un nombre fini de fonctions de base). Cependant, l'espace propre associé à une valeur propre donnée λ est unidimensionnel. Il est l'ensemble de toutes les fonctions 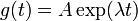 , où A est une constante arbitraire, la population initiale à t = 0 .
, où A est une constante arbitraire, la population initiale à t = 0 .
Théorème spectral
Dans sa version la plus simple, les Etats théorème spectral que, sous certaines conditions, une transformation linéaire d'un vecteur v peut être exprimée comme une combinaison linéaire des vecteurs propres, dans lequel le coefficient de chaque vecteur propre est égale à la fois valeur propre correspondante l' produits scalaire (ou produit scalaire) du vecteur propre avec le vecteur v . Mathématiquement, on peut écrire:
où v 1 , v 2 , ... et λ 1 , λ 2 , ... stand pour les vecteurs propres et les valeurs propres de T . Le théorème est valable pour toutes les transformations linéaires auto-adjoints (transformations linéaires donnés par de véritables matrices symétriques et matrices hermitiennes), et pour la classe plus générale de ( complexes ) matrices normales.
Si l'on définit le n de la puissance de la transformation à la suite de l'appliquer n fois de suite, on peut également définir des polynômes de transformations. Une version plus générale du théorème est que tout polynôme P de T est donnée par
Le théorème peut être étendu à d'autres fonctions de transformations, telles queles fonctions analytiques, le cas le plus général étantfonctions Borel.
Eigendecomposition
Le théorème spectral pour les matrices peut être énoncé comme suit. Soit A un carré n × n matrice. Soit q 1 ... q k soit une base de vecteurs propres, à savoir un ensemble indexé de k vecteurs propres linéairement indépendants, où k est la dimension de l'espace engendré par les vecteurs propres de A . Si k = n , alors A peut être écrite
oùQest le carrén×nmatrice dont lesième colonne est le vecteur propre baseq jedeAetΛest lamatrice diagonale dont la diagonale éléments sont les valeurs propres correspondantes, à savoirΛ je je= λje.
Des espaces de dimension infinie
Si l'espace vectoriel de dimension infinie est un espace de Banach, la notion de valeurs propres peut être généralisée à la notion de spectre. Le spectre est l'ensemble des scalaires λ pour laquelle ( T - λ) -1 est pas défini; qui est, de sorte que T - λ n'a pas borné inverse.
Il est clair que si λ est une valeur propre de T , λ est dans la gamme de T . En général, l'inverse est impossible. Il existe des opérateurs sur Hilbert ou espaces de Banach qui ne disposent pas du tout des vecteurs propres. Ceci peut être vu dans l'exemple suivant. Le décalage bilatéral sur l'espace de Hilbert ℓ 2 ( Z ) (autrement dit, l'espace de toutes les séquences de scalaires ... un -1 , un 0 , un 1 , un 2 , ... de telle sorte que
converge) n'a pas de valeur propre mais il a des valeurs spectrales.
Dans les espaces de dimension infinie, le spectre d'un opérateur borné est toujours non vide. Cela est également vrai pour un illimitée opérateur auto adjoint. Via ses mesures spectrales, le spectre d'un opérateur auto-adjoint, bornés ou non, peut être décomposé en absolument continue, pur point, et des pièces singulières. (Voir La décomposition du spectre.)
Fonctions exponentielles sont fonctions propres de l'opérateur de dérivée (la dérivée de fonctions exponentielles sont proportionnelles à themself). La croissance exponentielle et décroissance fournissent donc des exemples de spectres continus, de même que l'exemple de corde vibrante illustré ci-dessus. Le atome d'hydrogène est un exemple où les deux types de spectres apparaîtra. Les fonctions propres de l' hamiltonien d'un atome d'hydrogène sont appelés états propres et sont regroupés en deux catégories. Le états liés de l'atome d'hydrogène correspondent à la partie discrète du spectre (ils ont un ensemble discret de valeurs propres qui peut être calculée par la formule Rydberg) tandis que l' ionisation procédés sont décrits par la partie continue (l'énergie de la collision / ionisation non quantifiés).
Applications
Équation de Schrödinger

Un exemple d'une équation aux valeurs propres où la transformationTest représenté en termes d'un opérateur différentiel est le temps-indépendanteéquation de Schrödinger dansla mécanique quantique:
oùH, l'hamiltonien, est un second ordreopérateur différentiel et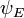 , Le fonction d'onde, est l'une de ses fonctions propres correspondant à la valeur propreE, interprétées comme sonénergie.
, Le fonction d'onde, est l'une de ses fonctions propres correspondant à la valeur propreE, interprétées comme sonénergie.
Toutefois, dans le cas où l'on est intéressé seulement dans les solutions d'État lié de l'équation de Schrödinger, on cherche 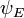 dans l'espace des fonctions de carré intégrable. Depuis cet espace est un espace de Hilbert avec une bien définie produit scalaire, on peut introduire un ensemble de base dans lequel
dans l'espace des fonctions de carré intégrable. Depuis cet espace est un espace de Hilbert avec une bien définie produit scalaire, on peut introduire un ensemble de base dans lequel 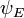 et H peut être représenté comme un tableau à une dimension et une matrice respectivement. Ce permet de représenter l'équation de Schrödinger dans une forme de matrice. (Fig. 4 présente les fonctions propres les plus bas de l' atome d'hydrogène hamiltonien.)
et H peut être représenté comme un tableau à une dimension et une matrice respectivement. Ce permet de représenter l'équation de Schrödinger dans une forme de matrice. (Fig. 4 présente les fonctions propres les plus bas de l' atome d'hydrogène hamiltonien.)
Le Notation de Dirac est souvent utilisé dans ce contexte. Un vecteur, ce qui représente un état du système, dans l'espace de Hilbert des fonctions intégrables carrés est représenté par 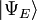 . Dans cette notation, l'équation de Schrödinger est:
. Dans cette notation, l'équation de Schrödinger est:
où 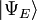 est un état propre de H . C'est un opérateur auto adjoint, l'analogue en dimension infinie des matrices hermitiennes ( voir Observable ). Comme dans le cas de la matrice, dans l'équation ci-dessus
est un état propre de H . C'est un opérateur auto adjoint, l'analogue en dimension infinie des matrices hermitiennes ( voir Observable ). Comme dans le cas de la matrice, dans l'équation ci-dessus 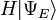 , on entend le vecteur obtenu par application de la transformation H à
, on entend le vecteur obtenu par application de la transformation H à 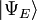 .
.
Orbitales moléculaires
Dans la mécanique quantique , et en particulier dans atomique et moléculaire physique , à l'intérieur de la théorie Hartree-Fock, les atomique et orbitales moléculaires peut être défini par les vecteurs propres de l' opérateur Fock. Les valeurs propres correspondantes sont interprétées comme des potentiels d'ionisation par le théorème de Koopmans. Dans ce cas, le vecteur propre terme est utilisé dans un sens un peu plus générale, étant donné que l'opérateur de Fock est explicitement dépendante des orbitales et leurs valeurs propres. Si l'on veut souligner cet aspect on parle d' équation aux valeurs propres implicite . Ces équations sont généralement résolus par une procédure d'itération, appelée dans ce cas méthode du champ auto-cohérent. Dans la chimie quantique , on représente souvent l'équation de Hartree-Fock dans un non orthogonale base indiquée. Cette représentation particulière est un problème aux valeurs propres généralisé appelé équations Roothaan.
Géologie et glaciologie: (Orientation Tensor)
En géologie , en particulier dans l'étude de till glaciaire, vecteurs et valeurs propres sont utilisés comme une méthode par laquelle une masse d'informations de l'orientation et le pendage de les constituants d'un clast tissu peut être résumée dans un espace 3-D de six chiffres. Sur le terrain, un géologue peut recueillir de telles données pour des centaines ou des milliers de fragments dans un échantillon de sol, qui ne peuvent être comparées graphiquement comme dans un Tri-Terrain (Sneed et Folk) diagramme, ou comme un stéréographique sur un Wulff Net . La sortie pour le tenseur d'orientation est dans les trois axes orthogonaux (perpendiculaires) de l'espace. Vecteurs propres sortie de programmes tels que Stereo32 sont dans l'ordre E1> E2> E3, E1 étant l'orientation première de l'orientation clast / immersion, E2 étant le secondaire et E3 étant le tertiaire, en termes de force. L'orientation clast est défini comme le vecteur propre, sur une rose des vents de 360 °. Dip est mesurée comme la valeur propre, le module du tenseur: ce sont évalués à partir de 0 ° (pas dip) à 90 ° (vertical). Diverses valeurs de E1, E2 et E3 signifient des choses différentes, comme on peut le voir dans le livre «Un guide pratique à l'étude de sédiments glaciaires» par Benn & Evans, 2004.
L'analyse factorielle
En l'analyse factorielle, les vecteurs propres d'une matrice de covariance ou de corrélation de la matrice correspondent aux éléments, et les valeurs propres à la variance expliquée par ces facteurs. L'analyse factorielle est une statistique technique utilisée dans les sciences sociales et dans marketing, la gestion des produits, la recherche opérationnelle , et d'autres sciences appliquées qui traitent de grandes quantités de données. L'objectif est d'expliquer la plupart des covariabilité parmi un certain nombre d'observables variables aléatoires en termes d'un plus petit nombre de variables latentes non observables appelées facteurs. Les variables aléatoires observables sont modélisés comme des combinaisons linéaires des facteurs, en plus de termes de variance uniques. Les valeurs propres sont utilisés dans l'analyse utilisé par le logiciel Q-méthodologie; facteurs avec des valeurs propres supérieures à 1,00 sont considérés comme importants, expliquant une quantité importante de la variabilité dans les données, tandis que les valeurs propres inférieures à 1,00 sont considérées comme trop faible, ne pas expliquer une partie significative de la variabilité des données.
Eigenfaces
En traitement d'image, les images traitées de faces peut être considéré comme des vecteurs dont les composantes sont les luminosités de chaque pixel. La dimension de cet espace vectoriel est le nombre de pixels. Les vecteurs propres de la matrice de covariance associée à un grand ensemble d'images normalisées de visages sont appelés eigenfaces; ceci est un exemple d' analyse en composantes principales. Ils sont très utiles pour exprimer toute image de visage comme une combinaison linéaire de certains d'entre eux. Dans le reconnaissance faciale branche de la biométrie, eigenfaces fournir un moyen d'appliquer la compression de données aux visages pour des fins d'identification. Recherche liée aux systèmes de vision propres déterminants gestes de la main ont également été réalisés. Plus sur la détermination de lettres en langue des signes à l'aide propres systèmes peuvent être trouvés ici: http://www.geigel.com/signlanguage/index.php
Semblable à ce concept, les voix propres concept est également développé qui représente la direction générale de la variabilité des prononciations humains d'une énonciation particulière, comme un mot dans une langue. Basé sur une combinaison linéaire de ces voix propres, une nouvelle voix de la prononciation de la parole peut être construit. Ces concepts ont été trouvés utiles dans les systèmes de reconnaissance automatique de la parole, pour l'adaptation au locuteur.
Tenseur d'inertie
En mécanique, les vecteurs propres de latenseur d'inertie définissent lesaxes principaux d'uncorps rigide. Le tenseur inertie est une clé quantité nécessaire pour déterminer la rotation d'un corps rigide autour de soncentre de masse.
Tenseur
En mécanique des solides, le tenseur des contraintes est symétrique et peut donc être décomposé en un tenseur diagonale avec les valeurs propres sur la diagonale et les vecteurs propres comme base. Parce qu'il est diagonale, dans cette orientation, le tenseur des contraintes n'a pas d' éléments de cisaillement; les composants, il ne dispose sont les composantes principales.
Les valeurs propres d'un graphe
En théorie des graphes spectrale, une valeur propre d'un graphe est défini comme une valeur propre de du graphique matrice d'adjacence l'un , ou (de plus en plus) de du graphique matrice de Laplace, qui est soit T - A ou I - T 1/2 AT -1/2 , où T est une matrice support diagonal le degré de chaque sommet, et en T -1/2 , 0 est substitué à 0 -1/2 . Le k ème vecteur propre principal d'un graphe est défini comme étant le vecteur propre correspondant à la k ième plus grande valeur propre de A , ou le vecteur propre correspondant à la k ième plus petite valeur propre du Laplacien. Le premier vecteur propre principal du graphique est également appelée simplement comme le vecteur propre capital.
Le vecteur propre capital est utilisé pour mesurer la centralité de ses sommets. Un exemple est Google l ' algorithme de PageRank. Le vecteur propre principal d'une modification de la matrice de contiguïté du Monde graphique Wide Web donne les rangs de page que ses composants. Ce vecteur correspond à la distribution stationnaire de la chaîne de Markov représenté par la matrice de contiguïté rangée normalisée; Cependant, la matrice d'adjacence doit d'abord être modifié pour assurer une distribution stationnaire existe. Le deuxième vecteur propre principal peut être utilisé pour partitionner le graphique en grappes, par l'intermédiaire de la classification spectrale. D'autres méthodes sont également disponibles pour le clustering.


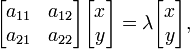
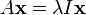
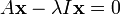
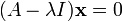
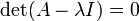
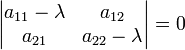
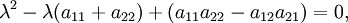
![\ Lambda_ {1,2} = \ frac {1} {2} \ left [(a_ {11} + a_ {22}) \ h \ sqrt {4A_ {12} {21} a_ + (a_ {11} - a_ {22}) ^ 2} \ right].](../../images/149/14952.png)