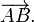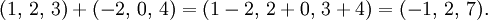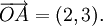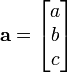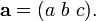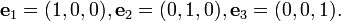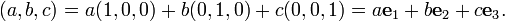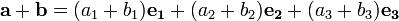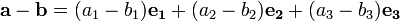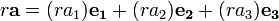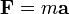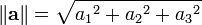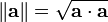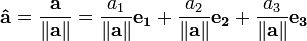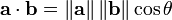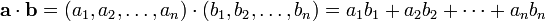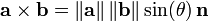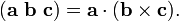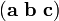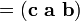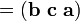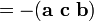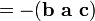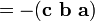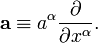Vectoriel euclidien

Un vecteur allant de A à B.

Un vecteur spatial, ou simplement vecteur, est un objet géométrique qui a à la fois une ampleur et une direction. Un vecteur est souvent représenté par un segment de ligne reliant le point initial A au point B et la borne notée

L'ampleur est la longueur du segment et la direction caractérise le déplacement de B par rapport à A: combien on doit déplacer le point A à "porter" au point B.

Beaucoup opérations algébriques sur les nombres réels ont analogues proches pour les vecteurs. Les vecteurs peuvent être ajoutées , soustraites , multipliées par un certain nombre, et retournées autour de sorte que la direction est inversée. Ces opérations obéissent aux lois algébriques familiers: la commutativité , associativité , distributivité. La somme de deux vecteurs avec le même point de départ peut être trouvée en utilisant l'géométriquement la loi de parallélogramme. La multiplication par un nombre positif, communément appelé un scalaire dans ce contexte, se élève à modifier la grandeur du vecteur, ce est-à étirer ou comprimer tout en conservant sa direction; multiplication par -1 préserve l'amplitude du vecteur mais inverse sa direction.

Coordonnées cartésiennes fournissent un moyen systématique de décrire les vecteurs et les opérations sur eux. Un vecteur devient un triplet de nombres réels, ses composants. L'addition de vecteurs et un vecteur de multiplication par un scalaire est effectuée simplement composante par composante, voir vecteur de coordonnées.

Vecteurs jouent un rôle important dans la physique : la vitesse et l'accélération d'un objet en mouvement et les forces agissant sur un corps sont tous décrits par des vecteurs. Beaucoup d'autres grandeurs physiques peuvent être considérés comme des vecteurs de utilement. Il faut garder à l'esprit, cependant, que les composantes d'un vecteur physique dépendent de la Système utilisé pour décrire de coordonnées. Autres objets vectoriels comme décrivant des quantités physiques et transforment d'une manière similaire en vertu des modifications du système de coordonnées comprennent pseudovectors et tenseurs.

Vue d'ensemble

De façon informelle, un vecteur est une quantité caractérisé par un grandeur (en mathématiques un certain nombre, en physique un certain nombre de fois par unité) et une direction, souvent représentés graphiquement par une flèche. Parfois, on parle de vecteurs liés ou fixes, qui sont des vecteurs dont le point initial est le origine. Ceci est en contraste aux vecteurs libres, qui sont des vecteurs dont le point initial ne est pas nécessairement l'origine.

Utilisez en physique et en ingénierie

Les vecteurs sont fondamentale dans les sciences physiques. Ils peuvent être utilisés pour représenter ne importe quelle quantité qui a à la fois une amplitude et une direction, tels que la vitesse , l'amplitude de ce qui est vitesse. Par exemple, la vitesse de 5 mètres par seconde vers le haut peuvent être représentées par le vecteur (0,5). Une autre quantité représentée par un vecteur est active , car il a une amplitude et une direction. Vecteurs décrivent également d'autres grandeurs physiques, telles que déplacement, l'accélération , électrique et champs magnétiques, l'élan , et le moment angulaire .

Vecteurs dans l'espace cartésien

En coordonnées cartésiennes , un vecteur peut être représenté par identifier les coordonnées de son point initial et terminal. Par exemple, les points A = (1,0,0) et B = (0,1,0) dans l'espace libre de déterminer le vecteur 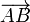pointant du point x = 1 sur la y axe des x au point = 1 sur le axe des y.

Typiquement en coordonnées cartésiennes, on considère vecteurs principalement liés. Un vecteur lié est déterminée par les coordonnées du point terminal, son point initial ayant toujours les coordonnées de l'origine O = (0,0,0). Ainsi le vecteur lié représenté par (1,0,0) est un vecteur de longueur unitaire pointant depuis l'origine jusqu'à l'axe des x positifs.

La représentation des coordonnées des vecteurs permet les fonctions algébriques de vecteurs de se exprimer de façon numérique pratique. Par exemple, la somme des vecteurs (1,2,3) et (-2,0,4) est le vecteur

Vecteurs et les vecteurs de affine euclidien

Dans les paramètres géométriques et physiques, il est parfois possible d'associer, d'une manière naturelle, une longueur des vecteurs ainsi que la notion d'un angle entre deux vecteurs. Lorsque la longueur des vecteurs est défini, il est également possible de définir un produit scalaire - un produit scalaire à valeur de deux vecteurs - ce qui donne une caractérisation algébrique commode à la fois de la longueur et de l'angle. Dans les trois dimensions, il est en outre possible de définir un produit vectoriel qui fournit une caractérisation algébrique de zone.

Toutefois, il ne est pas toujours possible ou souhaitable de définir la longueur d'un vecteur d'une manière naturelle. Ce type plus général de vecteur spatial est l'objet d' espaces vectoriels (pour les vecteurs liés) et espaces affines (pour des vecteurs libres).

Généralisations

En plus générales sortes de systèmes, les rotations d'un vecteur (et également de coordonner tenseurs) peuvent être généralisés et classés d'admettre une caractérisation analogue par leur covariance et contravariance dans les changements de coordonnées.

En mathématiques , un vecteur est considérée comme plus qu'une représentation d'une grandeur physique. En général, un vecteur est un élément d'un espace vectoriel sur certaines domaine. Les vecteurs spatiaux de cet article sont un cas très particulier de cette définition générale (ils ne sont pas tout simplement tout élément de R ^d dans les dimensions d), qui comprend une variété d'objets mathématiques ( algèbres, le ensemble de toutes les fonctions d'une donnée domaine à un linéaire donnée plage, et transformations linéaires). Notez que dans cette définition, un tenseur est un vecteur spécial.

Représentation d'un vecteur

Vecteurs sont habituellement notés en gras, comme un. D'autres conventions comprennent 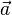ou un, en particulier à la main. Alternativement, certains utilisent un tilde (~) ou un trait de soulignement ondulé établi sous le symbole, qui est une convention pour indiquer le type de gras.

Les vecteurs sont généralement présentés sous forme de graphiques ou d'autres schémas que des flèches, comme illustré ci-dessous:

Ici, le point A est appelé le point initial, la queue, ou la base; point B est appelé la tête, une astuce, ou le terminal. La longueur de la flèche représente la magnitude du vecteur, tandis que la direction dans laquelle la flèche représente la direction du vecteur.

Dans la figure ci-dessus, la flèche peut aussi se écrire 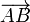ou AB.

Sur un diagramme à deux dimensions, parfois un vecteur perpendiculaire au plan du diagramme est souhaité. Ces vecteurs sont généralement indiqués par de petits cercles. Un cercle avec un point au centre indique un vecteur pointant hors de l'avant de la figure, vers l'observateur. Un cercle avec une croix inscrite dans cela indique un pointage de vecteur dans et derrière le diagramme. Ceux-ci peuvent être considérées comme la pointe d'un affichage flèche avant sur l'affichage et les aubes d'une flèche à l'arrière.

Un vecteur dans le plan cartésien, avec critère (2,3). Le vecteur se est identifié avec son extrémité.

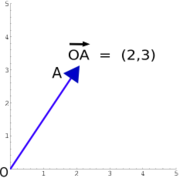
Afin de calculer avec des vecteurs, la représentation graphique peut être trop lourd. Vecteurs dans un espace de dimension euclidienne de n peuvent être représentées dans un système de coordonnées cartésiennes . Le critère d'évaluation d'un vecteur peut être identifié avec une liste de n nombres réels, parfois appelé vecteur ligne ou vecteur colonne. A titre d'exemple en deux dimensions (voir image), le vecteur de l'origine O = (0,0) au point A = (2,3) est simplement écrit

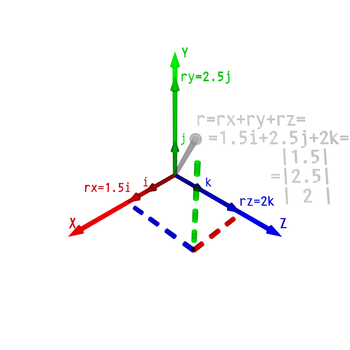
Dans l'espace euclidien à trois dimensions (ou R ^3), les vecteurs sont identifiés par des triplets de nombres correspondant aux coordonnées cartésiennes du point d'extrémité (a, b, c). Ces numéros sont souvent disposés dans un vecteur de colonne ou de rangée vecteur, en particulier lorsqu'il se agit de matrices , comme suit:

Une autre façon d'exprimer un vecteur en trois dimensions est d'introduire les trois coordonner vecteurs de base, parfois appelé vecteurs unitaires:

Ceux-ci ont l'interprétation intuitif comme vecteurs de longueur unitaire pointant vers le haut des x, y et l'axe z, respectivement. En termes de ceux-ci, tout vecteur dans R ³ peut être exprimée sous la forme:

Remarque: Dans les classes d'introduction à la physique, ces trois vecteurs spéciaux sont souvent désignés à la place i, j, k (ou 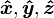quand en coordonnées cartésiennes ), mais ces affrontements de notation avec le notation d'index et le convention de sommation couramment utilisé dans les mathématiques de niveau supérieur, la physique et l'ingénierie. Cet article va choisir d'utiliser e _1, e _2, e _3.

L'utilisation de vecteurs unitaires cartésiennes 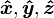comme un base dans laquelle pour représenter un vecteur, ne est pas obligatoire. Les vecteurs peuvent également être exprimés en termes de vecteurs unitaires cylindriques 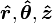ou sphériques vecteurs unitaires 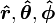. Ces deux dernières options sont plus commodes pour résoudre les problèmes qui possèdent une symétrie sphérique ou cylindrique, respectivement.

L'addition et la multiplication par un scalaire

Vecteur égalité

Deux vecteurs sont dits être égales si elles ont la même amplitude et la direction. Toutefois, si nous parlons des vecteurs libres, puis deux vecteurs libres sont égales si elles ont le même point de base et le point final.

Par exemple, le vecteur e ₁ + 2 + 3 e ₂ e ₃ avec un point de base (1,0,0) et le vecteur e 2 e _{1 2} 3 e ₃ avec un point de base (0,1,0) sont différents vecteurs libres, mais le même (déplacement) vecteur.

plus de Vector et la soustraction

Soit a = a ₁ e ₁ + a ₂ e ₂ + a ₃ e ₃ et b = b ₁ e ₁ + b ₂ e ₂ + b ₃ e _3, e _1, e _2, e ₃ sont des vecteurs unitaires orthogonaux (Note : ils ne doivent être linéairement indépendant, dire non parallèle et non dans le même plan, pour ces addition et de soustraction règles algébriques se appliquent)

La somme de a et b est la suivante:

L'addition peut être représenté graphiquement en plaçant le début de la flèche b à la pointe de la flèche a, puis en tirant une flèche à partir du début d'une à la pointe de b. La nouvelle flèche tracée représente le vecteur a + b, comme illustré ci-dessous:

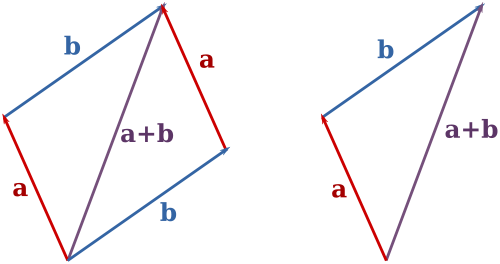
Cette méthode d'addition est parfois appelé la règle du parallélogramme parce A et B forment les côtés d'un parallélogramme et a + b est l'une des diagonales. Si a et b sont des vecteurs libres, puis l'addition ne est défini si A et B ont le même point de base, qui sera alors aussi le point de a + b de base. On peut vérifier géométriquement que a + b = b + a et (a + b) + c = a + (b + c).

La différence de a et b est la suivante:

Soustraction de deux vecteurs peut être géométriquement définie comme suit: pour soustraire b à partir d'un, placer les extrémités des a et b au même point, puis dessiner une flèche de la pointe de b à la pointe d'un. Ce flèche représente le vecteur a - b, comme illustré ci-dessous:

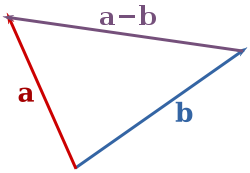
Si a et b sont des vecteurs libres, puis la soustraction ne est défini que si elles partagent le même point de base qui deviendra aussi le point de leur différence de base. Cette opération mérite le nom de "soustraction" parce que (a - b) + b = a.

Multiplication scalaire

Un vecteur peut également être multiplié, ou remplacé échelle, par un nombre réel r. Dans le contexte de vecteurs spatiaux, ces nombres réels sont souvent appelés des scalaires (de l'échelle) pour les distinguer des vecteurs. L'opération consistant à multiplier un vecteur par un scalaire est appelé multiplication scalaire. Le vecteur résultant est:

Multiplication scalaire d'un vecteur par un facteur de 3 se étend sur le vecteur.

Intuitivement, la multiplication par un scalaire r se étend d'un vecteur par un facteur de r. Géométriquement, cela peut être visualisé (au moins dans le cas où r est un entier) que de placer r copies du vecteur dans une ligne où le point final d'un vecteur est le point de départ du vecteur suivant.

Si r est négatif, alors le vecteur change de direction: il est éjecté autour d'un angle de 180 °. Deux exemples (r = r = 1 et 2) sont donnés ci-dessous:

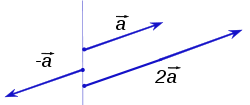
Multiplication scalaire est distributive sur l'addition de vecteur dans le sens suivant: r (a + b) = r a r + b pour tous les vecteurs a et b et toutes les scalaires r. On peut aussi montrer que a - b = a + (-1) b.

L'ensemble de tous les vecteurs géométriques, ainsi que les opérations d'addition de vecteur et multiplication par un scalaire, satisfait tous les axiomes d'un espace vectoriel . De même, l'ensemble de tous les vecteurs liés avec un point de base commune constitue un espace vectoriel. Ce est là que le terme «espace vectoriel» est née.

En physique, scalaires peuvent également avoir une unité de mesure qui leur est associée. Par exemple, la seconde loi de Newton est

où F a des unités de force, une a unités de l'accélération et le scalaire m a unités de masse. Dans une possible interprétation physique du schéma ci-dessus, l'échelle de l'accélération est, par exemple, 2 m / s ^2: cm, et celle de la force 5 N: cm. Ainsi, un rapport d'échelle de 2,5 kg: 1 est utilisé pour la messe. De même, si le déplacement a une échelle de 1: 1000 et la vitesse de 0,2 cm: 1 m / s, ou équivalente, 2 ms: 1, un rapport d'échelle de 0,5: s est utilisé pour le temps.

La longueur et le produit scalaire

Longueur d'un vecteur

Le longueur ou ampleur ou norme du vecteur est désigné par un || a || ou, moins fréquemment, | a |, qui ne doit pas être confondue avec la valeur absolue (un scalaire "norme").

La longueur du vecteur a = a ₁ e ₁ + e _{2 2} + a _{3 3} e dans une tridimensionnel espace euclidien , où e _1, e _2, e ₃ sont des vecteurs unitaires orthogonaux, peut être calculée avec la Norme euclidienne

qui est une conséquence du théorème de Pythagore depuis la vecteurs de base e _1, e _2, e ₃ sont des vecteurs unitaires orthogonaux.

Cela arrive à être égale à la racine carrée de la dot produit du vecteur avec lui-même:

Longueur du vecteur et unités

Si un vecteur spatial est elle-même, la longueur de la flèche dépend d'un dimension échelle. Si elle représente par exemple une force, «l'échelle» est de Dimension Longueur / force physique. Ainsi, il est généralement la cohérence à l'échelle entre les quantités de la même dimension, mais sinon l'échelle ratios peuvent varier; Par exemple, si "1 newton" et "5 m" sont tous deux représentés par une flèche de 2 cm, les échelles sont 1: 250 et 1 m: 50 N respectivement. Égale longueur de vecteurs de dimension différente n'a pas de signification particulière, sauf si il ya une certaine constante de proportionnalité inhérent au système que représente le diagramme. Aussi longueur d'un vecteur de l'unité (de la longueur de dimension, pas de longueur / force, etc.) n'a pas de coordonnées système invariant importance.

vecteur d'unité

Un vecteur unitaire est ne importe quel vecteur d'une longueur de un; géométriquement, il indique une direction mais pas de grandeur. Si vous avez un vecteur de longueur arbitraire, vous pouvez diviser par sa longueur pour créer un vecteur unitaire. Ceci est connu comme normaliser un vecteur. Un vecteur de l'unité est souvent indiqué avec un chapeau comme dans un.

Pour normaliser un vecteur a = [A _1, A _{2, 3],} l'échelle le vecteur par l'inverse de sa longueur || a ||. C'est:

Vecteur nul

Le vecteur nul (ou vecteur nul) est le vecteur avec une longueur nulle. Écrite en coordonnées, le vecteur est (0,0,0), et il est communément désigné 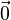, Ou 0, ou tout simplement 0. Contrairement à tout autre vecteur, il n'a pas de sens, et ne peut être normalisée (ce est à dire, il n'y a pas vecteur unitaire qui est un multiple du vecteur nul). La somme du vecteur nul avec un quelconque vecteur est un (ce est à dire, 0 + a = a).

Produit scalaire

Article détaillé: Produit scalaire

Le produit scalaire de deux vecteurs A et B (parfois appelé le produit scalaire, ou, depuis son résultat est un scalaire, le produit scalaire) est désignée par un ∙ et b est défini comme:

où || a || et || b || désigner le norme (ou longueur) de a et b, et θ est la mesure de l' angle entre a et b (voir fonction trigonométrique pour une explication de cosinus). Géométriquement, cela signifie que A et B sont tirés avec un point de départ commun et la longueur d'une multipliée par la longueur de cet élément de b qui pointe dans la même direction que a.

Le produit scalaire peut également être défini comme la somme des produits des composantes de chaque vecteur:

où a et b sont des vecteurs de dimension n; a _1, a _2, ..., a _n sont des coordonnées d'un; et b _1, b _2, ..., b _n sont coordonnées de b.

Cette opération est souvent utile dans la physique ; par exemple, le travail est le produit scalaire de la force et déplacement.

Produit Croix

Le produit vectoriel (également appelée produit vectoriel ou produit externe) diffère du produit scalaire principalement en ce que le résultat du produit vectoriel de deux vecteurs est un vecteur. Alors que tout ce qui a été dit ci-dessus peut être généralisée de manière directe à plus de trois dimensions, le produit croisé n'a de sens que dans les trois dimensions, bien que la sept produit croisé dimensions est similaire à certains égards. Le produit vectoriel, noté A × B, est un vecteur perpendiculaire à la fois a et b et est défini comme:

où θ est la mesure de l'angle entre a et b, et n est un vecteur unitaire perpendiculaire à la fois a et b. Le problème avec cette définition est qu'il existe deux vecteurs unitaires perpendiculaire à la fois b et a.

Une illustration du produit croix.

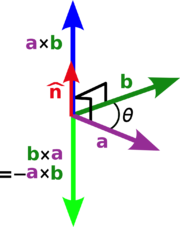
La base de vecteur e _1, e _2, e ₃ est appelé droitier, si les trois vecteurs sont situés comme le pouce, l'index et le majeur (pointant vers le haut de votre paume) de votre main droite. Graphiquement le produit croisé peut être représentée par la figure de droite.

Le produit une croix × b est définie de telle sorte que a, b, et a × b devient également un système à droite (mais notez que a et b sont pas nécessairement orthogonale). Ceci est le Règle de la main droite.

La longueur de a × b peut être interprété comme l'aire du parallélogramme ayant a et b en tant que côtés.

Pour des choix arbitraires de l'orientation spatiale (ce est à dire, ce qui permet pour les gauchers ainsi que droitier systèmes de coordonnées) le produit croisé de deux vecteurs est une pseudovector au lieu d'un vecteur (voir ci-dessous).

Triple produit scalaire

Le triple produit scalaire (appelé aussi le produit de boîte ou triple produit mixte) ne est pas vraiment un nouvel opérateur, mais un moyen d'appliquer les deux autres opérateurs de multiplication de trois vecteurs. Le produit scalaire triple est parfois désignée par (a b c), et défini comme suit:

Il a trois utilisations principales. Premièrement, la valeur absolue du produit de la boîte est le volume de la parallélépipède qui présente des bords qui sont définis par les trois vecteurs. Deuxièmement, le produit scalaire est triple zéro si et seulement si les trois vecteurs sont linéairement dépendante, qui peut être facilement prouvé en considérant que, pour que les trois vecteurs de ne pas ouvrir un volume, ils doivent tous se situer dans le même plan. Troisièmement, le produit de la boîte est positive si et seulement si les trois vecteurs a, b et c sont droitiers.

Dans les composants (par rapport à une base orthonormée droitier), si les trois vecteurs sont considérés comme des lignes (ou colonnes, mais dans le même ordre), le triple produit scalaire est simplement le facteur déterminant de la 3-en-3 matrice ayant les trois vecteurs que rangées. Le produit scalaire est linéaire triple dans les trois entrées et anti-symétrique dans le sens suivant:

Les composants du vecteur

Illustration des composantes tangentielles et normales d'un vecteur à une surface.

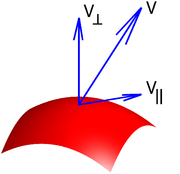
Un composant d'un vecteur est l'influence de ce vecteur dans une direction donnée. Les composants sont eux-mêmes vecteurs.

Un vecteur est souvent décrit par un nombre fixe de composants qui résument dans ce vecteur unique et totalement. Lorsqu'ils sont utilisés dans ce rôle, le choix de leurs directions constituant dépend du système de coordonnées particulier utilisé, comme coordonnées cartésiennes , coordonnées sphériques ou coordonnées polaires . Par exemple, une composante axiale du vecteur est telle que sa composante dont la direction est déterminée par l'une des coordonnées cartésiennes axes, tandis que le sens radial et composantes tangentielles se rapportent à la rayon de rotation d'un objet que leur direction de référence. Le premier est parallèle au rayon et celle-ci est orthogonal à elle. Deux restent orthogonaux à l'axe de rotation à tout moment. (Dans deux dimensions cette exigence devient redondant que l'axe dégénère à un point de rotation.) Le choix d'un système de coordonnées ne affecte pas les propriétés d'un vecteur ou son comportement sous transformations.

Vecteurs que dérivées directionnelles

Un vecteur peut également être défini comme un dérivée directionnelle: envisager une fonction 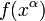et une courbe 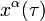. Ensuite, la dérivée directionnelle de 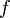est un scalaire défini comme

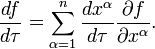
où l'indice est sommée sur le nombre approprié de dimensions (par exemple de 1 à 3, dans l'espace euclidien à 3 dimensions, de 0 à 3 dans l'espace-temps à 4 dimensions, etc.). Puis envisager un vecteur tangent à :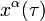

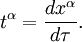
Nous pouvons réécrire la dérivée directionnelle sous forme différentielle (sans fonction donnée 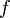) Comme

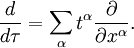
Par conséquent, toute dérivée directionnelle peut être identifié avec un vecteur correspondant, et tout vecteur peut être identifié avec une dérivée directionnelle correspondante. Nous pouvons donc définir un vecteur précisément:

Vecteurs, pseudovectors, et des transformations

Une alternative caractérisation des vecteurs spatiaux, en particulier en physique, décrit des vecteurs que des listes de quantités qui se comportent d'une certaine manière en vertu d'un transformation de coordonnées. Un vecteur est nécessaire d'avoir des composants qui "transformer comme les coordonnées" sous coordonner les rotations. En d'autres termes, si tout l'espace ont été tourné, le vecteur serait tourner exactement de la même façon. Mathématiquement, si le système de coordonnées décrit subit une rotation par une rotation matrice R, de telle sorte qu'un vecteur de coordonnées x est transformé en x '= x R, alors ne importe quel autre vecteur v doit être transformée de manière similaire par l'intermédiaire de v' = R c. Cette exigence importante est ce qui distingue un vecteur spatial de toute autre triplet de quantités significatives physiquement. Par exemple, si v est constitué des x, y et z -Composants de vitesse , alors v est un vecteur du fait que les composantes de la vitesse se transforment sous coordonner les changements. D'autre part, par exemple, un triplet constitué de la longueur, la largeur et la hauteur d'une boîte rectangulaire pourrait être considéré comme les trois composantes d'un résumé vecteur , mais pas un vecteur spatial, puisque la rotation de la boîte ne transforme pas en conséquence ceux-ci trois composants. Des exemples de vecteurs comprennent déplacement, vitesse , champ électrique , l'élan , la force et l'accélération .

Dans le langage de la géométrie différentielle , l'exigence selon laquelle les composantes d'un vecteur à transformer selon la même matrice de la transition de coordonnées est équivalent à définir un vecteur d'être tenseur contravariant rang un. Cependant, en géométrie différentielle et d'autres domaines de mathématiques tels que théorie de la représentation, les «coordonner transitions" ne doit pas être limitée aux rotations. Autres notions de vecteur spatial correspondent aux différents choix de groupe de symétrie.

Comme un cas particulier où le groupe de symétrie est important, tous les exemples ci-dessus sont des vecteurs qui "transforment comme les coordonnées" sous la fois appropriée et rotations inappropriées. Un exemple d'une mauvaise rotation est un reflet miroir. Autrement dit, ces vecteurs sont définis de telle manière que, si la totalité de l'espace ont été retournées autour à travers un miroir (ou autrement soumis à une rotation incorrecte), qui bascule autour de vecteur serait exactement de la même manière. Vecteurs ayant cette propriété sont appelés vrais vecteurs ou vecteurs polaires. Cependant, d'autres vecteurs sont définis d'une manière telle que, lors feuilletant un miroir, le vecteur retourne de la même manière, mais acquiert également un signe négatif. Ils sont appelés pseudovectors (ou vecteurs axiaux), et le plus souvent se produisent que des produits croisés de véritables vecteurs.

Un exemple d'un vecteur axial est un moment angulaire . Conduire dans une voiture , et je ai hâte, chacune des roues a un vecteur moment angulaire pointant vers la gauche. Si le monde se reflète dans un miroir qui commute le côté gauche et droit de la voiture, le reflet de cette angulaires points de vecteur de mouvement vers la droite, mais le vecteur de la roue d'inertie angulaire réelle pointe toujours vers la gauche, correspondant au moins signer. D'autres exemples comprennent des pseudovectors champ magnétique, couple, ou plus généralement tout produit vectoriel de deux vecteurs (vrai).

Cette distinction entre les vecteurs et pseudovectors est souvent ignorée, mais il devient important dans l'étude de symétrie propriétés. Voir parité (physique).