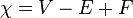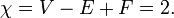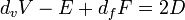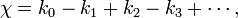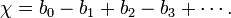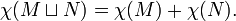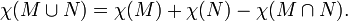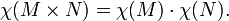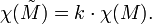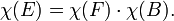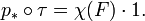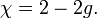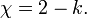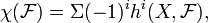Caractéristique d'Euler

À propos de ce écoles sélection Wikipedia

Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Avant de vous décider à propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur différents organismes de parrainage premier ?

En mathématiques , et plus spécifiquement dans topologie algébrique et combinatoire polyédriques, la caractéristique d'Euler (ou caractéristique d'Euler-Poincaré) est un invariant topologique, un nombre qui décrit un la forme ou la structure de l'espace topologique indépendamment de la façon dont il est plié. Il est communément désigné par 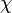$\ Chi$ ( lettre grecque chi).

La caractéristique d'Euler a été défini à l'origine pour les polyèdres et utilisé pour prouver divers théorèmes à leur sujet, y compris la classification des solides de Platon . Leonhard Euler , pour qui le concept est nommé, était en grande partie responsable de ce travail précoce. En mathématiques modernes, la caractéristique d'Euler découle de homologie et se connecte à de nombreux autres invariants.

Polyèdres

La caractéristique d'Euler 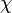$\ Chi$ a été définie de façon classique pour les surfaces de polyèdres, selon la formule

$\ Chi = V-E + F \, \!$

où V, E, et F sont respectivement les nombres de sommets (coins), bords et visages dans le polyèdre donné. La surface de tout polyèdre convexe a caractéristique d'Euler

$\ Chi = V - E + F = 2. \, \!$

Ce résultat est connu sous la formule d'Euler. Cela correspond à la caractéristique d'Euler de la sphère (qui est 2), et se applique de manière identique à polyèdres sphériques. Une illustration de la formule de certains polyèdres est donnée ci-dessous.

Nom	Sommets V	Bords E	Visages Fa	Caractéristique d'Euler: V - E + F
Tétraèdre	4	6	4	2
Hexahedron ou cube	8	12	6	2
Octaèdre	6	12	8	2
Dodécaèdre	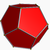20	30	12	2
Icosaèdre	12	30	20	2

Les surfaces de polyèdres non convexe peuvent avoir diverses caractéristiques d'Euler;

Nom	Sommets V	Bords E	Visages Fa	Caractéristique d'Euler: V - E + F
Tétrahémihexaèdre	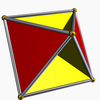6	12	7	1
Octahémioctaèdre	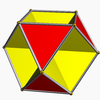12	24	12	0
Cubohémioctaèdre	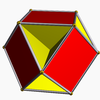12	24	10	-2
Grand icosaèdre	12	30	20	2

Une forme modifiée de la formule d'Euler, en utilisant polyédrique densité (D) et densité de polygone de la (chiffres vertex 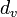$d_v$ ) Et des faces ( $D_F$ ) A été donné par Arthur Cayley, et détient à la fois pour polyèdres convexes (où les facteurs de correction sont tout 1), et le non-convexe régulière Polyèdres Kepler-Poinsot:

$d_v V - E + F = D_F 2D$

En outre, polyèdres projective ont tous une caractéristique d'Euler correspondant à la plan projectif réel, tout en polyèdres toroïdal ont tous Euler caractéristique 0, correspondant au tore .

Graphes planaires

La caractéristique d'Euler peut être défini pour connecté graphes planaires par le même 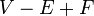$V - E + F$ formule que pour les surfaces polyédriques, où f est le nombre de faces dans le graphique, y compris la face extérieure.

La caractéristique d'Euler de tout graphe planaire est 2. Pour via la projection stéréographique plan mappe le domaine à deux dimensions, de telle sorte que les cartes de graphe à une décomposition polygonale de la sphère, ce qui a Euler caractéristique 2. Ce point de vue est implicite dans la preuve de Cauchy de la formule d'Euler donné ci-dessous.

Preuve de la formule d'Euler

Premières étapes de la preuve dans le cas d'un cube

La première preuve rigoureuse de la formule d'Euler, donnée par Cauchy en 1811, est la suivante.

Retirer une face de la surface polyédrique. En tirant sur les bords de la face cachée de distance l'une de l'autre, tout le reste se déformer dans un plan graphique de points courbes, comme illustré par la première des trois graphiques pour le cas particulier du cube. (L'hypothèse que la surface polyédrique est homéomorphe à la sphère au début est ce qui rend cela possible.) Après cette déformation, les visages réguliers ne sont généralement pas plus régulière. Le nombre de sommets et d'arêtes est resté le même, mais le nombre de faces a été réduit de 1. En tant que tel, ce qui prouve la formule d'Euler pour réduire le polyèdre à prouver V - E + F = 1 pour cela, objet plan déformé.

Se il ya un visage avec plus de trois côtés, dessiner une diagonale qui est, une courbe à travers la face reliant deux sommets qui ne sont pas encore connectés. Cela ajoute un bord et une face et ne modifie pas le nombre de sommets, de sorte qu'il ne change pas la quantité V - E + F. Continuez à ajouter des bords de cette manière jusqu'à ce que toutes les faces sont triangulaires.

Appliquer de façon répétée une ou l'autre des deux transformations suivantes:

Retirer un triangle avec un seul bord adjacent vers l'extérieur, comme illustré par le deuxième graphique. Ceci diminue le nombre d'arêtes et faces par une pièce et ne modifie pas le nombre de sommets, de sorte qu'il conserve V - E + F.
Retirer un triangle avec deux bords communs à l'extérieur du réseau, comme le montre la troisième courbe. Chaque retrait triangle supprime un sommet, deux bords et une face, de manière à préserver V - E + F.

Répétez ces deux étapes, l'une après l'autre, jusqu'à ce qu'un seul triangle reste.

A ce stade, seul le triangle a V = 3, E = 3 et F = 1, de sorte que V - E + F = 1. Etant donné que chacune des deux étapes de transformation ci-dessus conserve cette grandeur, nous avons montré V - E + F = 1 pour la déformer, objet plan qui démontre V - E + F = 2 pour le polyèdre. Cela prouve le théorème.

Pour preuves supplémentaires, voir Dix-neuf épreuves de la formule d'Euler par David Eppstein. Preuves multiples, y compris leurs défauts et leurs limites, sont utilisés comme exemples dans Preuves et Réfutations par Imre Lakatos.

Définition topologique

Les surfaces polyédriques évoqués ci-dessus sont, en langage moderne, deux de dimension finie CW-complexes. (Lorsque seules faces triangulaires sont utilisés, ils sont finis à deux dimensions complexes simpliciaux). En général, pour toute CW-complexe fini, la caractéristique d'Euler peuvent être définis comme la somme alternatif

$\ Chi = K_0 - k_1 + k_2 - k_3 + \ cdots, \$

où k _n désigne le nombre de cellules de dimension n dans le complexe.

Plus généralement encore, pour toute espace topologique, on peut définir la nième Betti nombre b _n que le rang de la n ième groupe d'homologie singulière. La caractéristique d'Euler peut alors être défini comme la somme alternée

$\ Chi = b_0 - b_1 + b_2 -. B_3 + \ cdots \$

Cette quantité est bien définie que si les nombres de Betti sont tous fini et, se ils sont égaux à zéro au-delà d'un certain indice n _0. Pour les complexes simpliciaux, ce ne est pas la même définition que dans le paragraphe précédent, mais un calcul d'homologie montre que les deux définitions donneront la même valeur pour 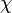$\ Chi$ .

Propriétés

Comme corollaire de Dualité de Poincaré, la caractéristique d'Euler de tout collecteur de dimension impaire fermé est nulle. Cela se applique plus généralement à tout compact espace stratifié dont toutes les strates sont de dimension impaire. En outre, la caractéristique d'Euler se comporte bien par rapport à de nombreuses opérations de base sur les espaces topologiques, comme suit.

Invariance Homotopie

Depuis l'homologie est un invariant topologique (en fait, un invariant d'homotopie - deux espaces topologiques qui sont l'équivalent homotopie avoir isomorphe groupes d'homologie), est donc la caractéristique d'Euler.

Par exemple, tout polyèdre convexe est homéomorphe à la tridimensionnel balle, donc sa surface est homéomorphe (d'où homotopie équivalent) pour les deux dimensions sphère , qui a caractéristique d'Euler 2. Cela explique pourquoi polyèdres convexes ont caractéristique d'Euler 2.

Principe d'inclusion-exclusion

Si M et N sont tous les deux espaces topologiques, alors la caractéristique d'Euler de leur union disjointe est la somme de leurs caractéristiques d'Euler, puisque homologie est additif par union disjointe:

$\ Chi (M \ sqcup N) = \ chi (M) + \ chi (N).$

Plus généralement, si M et N sont des sous-espaces d'un espace plus grand X, le sont aussi leur union et l'intersection. Dans certains cas, la caractéristique d'Euler obéit à une version de la principe d'inclusion-exclusion:

$\ Chi (M \ cup N) = \ chi (M) + \ chi (N) - \ chi (M \ cap N).$

Cela est vrai dans les cas suivants:

si M et N sont un quelques excisive. En particulier, si le intérieurs de M et N à l'intérieur de l'Union couvrent encore le syndicat.

si X est un espace localement compact, et on utilise les caractéristiques d'Euler avec compact supports, aucune hypothèse sur M ou N sont nécessaires.

si X est un espace stratifié dont toutes les strates sont même dimensions, le principe d'inclusion-exclusion détient si M et N sont des unions de strates. Cela vaut en particulier si M et N sont des sous-variétés d'un complexe variété algébrique.

En général, le principe d'inclusion-exclusion est faux. Un contre-est donnée en prenant X d'être le ligne réelle, M un sous-ensemble constitué d'un point et le N compléter de M.

propriété produit

En outre, la caractéristique d'Euler de toute espace produit M × N est

$\ Chi (M \ times n) = \ chi (M) \ cdot \ chi (N).$

Ces propriétés d'addition et de multiplication sont également appréciés par cardinal de jeux . De cette façon, la caractéristique d'Euler peut être considérée comme une généralisation de cardinal; voir .

Couvrant espaces

De même, pour un k -sheeted couvrant l'espace 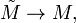$\ Tilde {M} \ M,$ on a

$\ Chi (\ tilde {M}) = k \ cdot \ chi (M).$

Plus généralement, pour un espace de revêtement ramifié, la caractéristique d'Euler de la couverture peut être calculé à partir de ce qui précède, avec un facteur de correction pour les points de ramification, ce qui donne le Formule de Riemann-Hurwitz.

Propriété Fibration

La propriété produit détient beaucoup plus généralement, pour fibrations avec certaines conditions.

Si 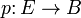$p \ colon E \ B$ est une fibration de fibre F, avec la base B chemin-connecté, et la fibration est orientable sur un corps K, alors la caractéristique d'Euler avec des coefficients dans le domaine K satisfait la propriété du produit:

$\ Chi (E) = \ chi (F) \ cdot \ chi (B).$

Cela comprend des espaces de produits et espaces couvrant que des cas particuliers, et peut être prouvé par le Suite spectrale Serre sur homologie d'une fibration.

Pour les faisceaux de fibres, ce peut aussi être comprise en termes d'un transfert carte 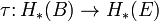$\ Tau \ colon H _ * (B) \ H _ * (E)$ - Noter que ce est une levée et va "dans le mauvais sens" - dont la composition avec la carte de projection 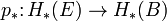$p _ * \ colon H _ * (E) \ H _ * (B)$ est la multiplication par Euler classe de la fibre:

$p_ * \ circ \ tau = \ chi (F) \ cdot 1.$

Relations avec les autres invariants

La caractéristique d'Euler d'une fermeture orientable surface peut être calculée à partir de son genre g (le nombre de tores en un relié somme décomposition de la surface; Intuitivement, le nombre de "poignées") en tant que

$\ Chi = 2 -. 2g \$

La caractéristique d'Euler d'une surface non-orientable fermé peut être calculée à partir de son genre non orientable k (le nombre de véritables plans projectifs dans une somme décomposition connexe de la surface) que

$\ Chi = 2 -. K \$

Pour les variétés lisses fermés, la caractéristique d'Euler coïncide avec le nombre d'Euler, à savoir la Euler classe de son fibré tangent évaluée sur la classe fondamentale d'un collecteur. La classe d'Euler, à son tour, se rapporte à tout autre classes caractéristiques de fibrés vectoriels.

Pour fermée Variétés riemanniennes, la caractéristique d'Euler peuvent également être trouvés en intégrant la courbure; voir le Formule de Gauss-Bonnet pour le cas à deux dimensions et la généralisée théorème de Gauss-Bonnet pour le cas général.

Un analogue discret du théorème de Gauss-Bonnet est Théorème de Descartes que la "défaillance totale" d'un polyèdre , mesurée en cercles complets, est la caractéristique d'Euler du polyèdre; voir défaut (géométrie).

Le théorème de Hadwiger caractérise la caractéristique d'Euler comme uniques ( jusqu'à multiplication par un scalaire) invariant par translation, additif fini, la fonction de jeu sans nécessairement défini non négatif sur- unions finies de compact convexe met en R ⁿ qui est "homogène de degré 0".

Exemples

La caractéristique d'Euler peut être calculée facilement générales pour les surfaces en trouvant une polygonisation de la surface (ce est aussi une description d'un CW-complexe) et en utilisant les définitions ci-dessus.

Nom	Image	Caractéristique d'Euler
Intervalle		1
Cercle		0
Disque		1
Sphère		2
Torus (Produit de deux cercles)		0
Tore doubles		-2
Tore Triple		-4
Plan projectif réel		1
Ruban de Möbius		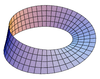0
La bouteille de Klein		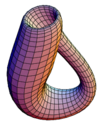0
Deux sphères (non relié) (Union disjointe de deux sphères)		2 + 2 = 4
Trois sphères (non relié) (Union disjointe de trois sphères)		2 + 2 + 2 = 6

Tout Espace contractile (ce est-à une homotopie équivalent à un point) présente une homologie trivial, ce qui signifie que le nombre de Betti 0e est une et les autres 0. Par conséquent, son caractéristique d'Euler est 1. Cette affaire comprend l'espace euclidien 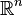$\ Mathbb {R} ^ n$ de ne importe quelle dimension, ainsi que la boule unité solide dans un espace euclidien - l'intervalle unidimensionnel, le disque à deux dimensions, la balle en trois dimensions, etc.

La sphère de dimension n a Betti numéro 1 dans les dimensions 0 et n, et tous les autres nombres de Betti 0. D'où sa caractéristique d'Euler est 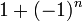$1 + (-1) ^ n$ - Ce est-à 0 ou 2.

Le n réelle de dimension espace projectif est le quotient de la n -sphere par la carte antipode. Il se ensuit que sa caractéristique d'Euler est exactement la moitié de celle de la sphère correspondant - 0 ou 1.

Le n tore de dimension est l'espace de produit de n cercles. Sa caractéristique d'Euler est 0, par la propriété du produit. Combien de pentagones et d'hexagones faut-il pour faire une Ballon de football? Supposons que nous utilisons 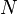$N$ hexagones et 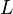$L$ pentagones; alors nous avons 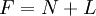$F = N + L$ visages. Chaque pentagone (hexagone) a 5 sommets (6 sommets), et chacun est partagée entre trois visages, donc nous avons 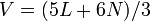$V = (5 + 6 L N) / 3$ sommets. De même, chaque pentagone (hexagone) a cinq bords (6) bords, et chacun est partagé entre les deux faces, d'où nous avons 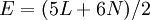$E = (L 5 + 6 N) / 2$ bords.

Étant donné que la sphère 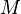$M$ a Euler caractéristique 2, il faut que $L = 12$ . Le résultat est que nous avons toujours besoin de 12 pentagones sur un ballon de football / soccer; le nombre d'hexagones est en principe sans contrainte (mais pour un ballon de football réel / football choisit évidemment un nombre qui rend la balle aussi sphérique que possible). On peut également appliquer ce résultat fullerènes.

Généralisations

Pour chaque combinatoire complexe de la cellule, on définit la caractéristique d'Euler que le nombre de cellules 0, moins le nombre de cellules d'ordre 1, plus le nombre de cellules-2, etc., si cette somme est finie alternatif. En particulier, la caractéristique d'Euler d'un ensemble fini est simplement son cardinal, et la caractéristique d'Euler d'un graphe est le nombre de sommets moins le nombre de bords.

Plus généralement, on peut définir la caractéristique d'Euler de tout complexe de chaîne à la somme alternée de la rangs des groupes d'homologie du complexe de la chaîne.

Une version utilisée dans géométrie algébrique est le suivant. Pour toute gerbe 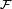$\ Scriptstyle \ mathcal {F}$ sur une projective schéma X, on définit sa caractéristique d'Euler

$\ Chi (\ mathcal {F}) = \ Sigma (-1) ^ ih ^ i (X, \ mathcal {F}),$

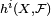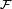où $\ Scriptstyle h ^ i (X, \ mathcal {F})$ est la dimension de la i -ième groupe de cohomologie gerbe de $\ Scriptstyle \ mathcal {F}$ .

Une autre généralisation du concept de caractéristique d'Euler sur les variétés vient de orbifolds. Bien que chaque collecteur a un entier caractéristique d'Euler, un orbifold peut avoir une caractéristique Euler fractionnée. Par exemple, le orbifold en goutte d'eau a une caractéristique Euler + 1 / p, où p est un nombre premier correspondant à l'angle de cône de 2 π / p.

Le concept de caractéristique d'Euler d'un fini borné poset est une autre généralisation, important dans la combinatoire . Un poset est "limitée" si elle a le plus petit et le plus grand des éléments; appeler 0 et 1. La caractéristique d'Euler d'un tel ensemble ordonné est définie comme l'entier μ (0,1), où μ est le Fonction de Möbius dans ce poset de algèbre incidence.

Ceci peut être généralisé en outre en définissant une caractéristique d'Euler Q -Évaluées pour certain fini catégories, une notion compatible avec les caractéristiques d'Euler de graphiques, orbifolds et posets mentionnés ci-dessus. Dans ce cadre, la caractéristique d'Euler d'un fini groupe ou monoid G est 1 / | G |, et la caractéristique d'Euler d'un fini groupoïde est la somme de 1 / | G _i |, où nous avons un groupe représentant G _i pour chaque composante connexe de l'groupoïde.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Euler_characteristic&oldid=379691924 "

We provide Linux to the World