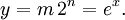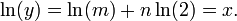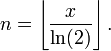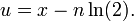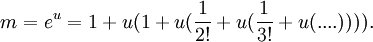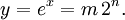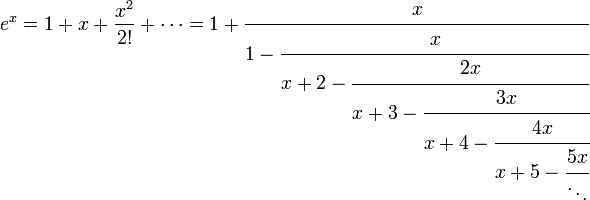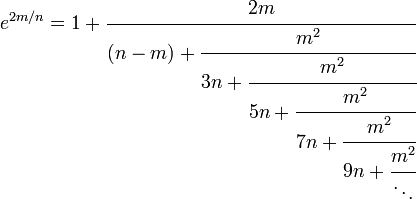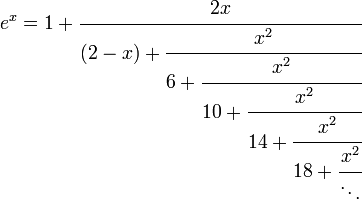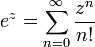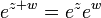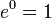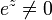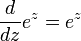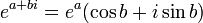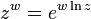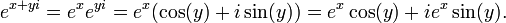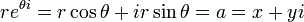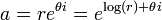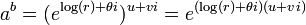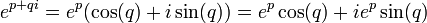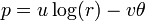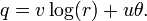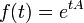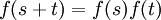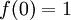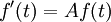Fonction exponentielle
Saviez-vous ...
Cette sélection Wikipedia est déconnecté disponibles à partir enfants SOS pour la distribution dans le monde en développement. Parrainage d'enfants aide les enfants du monde en développement à apprendre aussi.
La fonction exponentielle est une fonction dans les mathématiques . L'application de cette fonction pour une valeur x se écrit exp (x). Équivalente, ce qui peut être écrit sous la forme e x, où e est une constante mathématique, le base du logarithme naturel, qui est approximativement égale à 2,718281828, et est également connu comme Euler numéro.

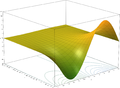
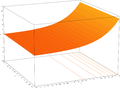
En fonction des réels x variable, le graphique de y = x e est toujours positive (au-dessus de l'axe des x) et en augmentant (vue de gauche à droite). Il ne touche jamais l'axe x, même si elle obtient arbitrairement proche (ainsi, l'axe des x est un axe horizontal asymptote de la courbe). Sa fonction inverse , le logarithme naturel , ln (x), est défini pour tout x positif. La fonction exponentielle est parfois dénommé anti-logarithme . Toutefois, cette terminologie semble être tombé en désuétude ces derniers temps.
Parfois, en particulier dans les sciences , la fonction terme exponentiel est plus généralement utilisé pour des fonctions de la forme ka x, où a, appelé la base, est un nombre réel positif non égal à un. Cet article se concentrera initialement sur la fonction exponentielle avec la base e, nombre d'Euler.
En général, la x variables peuvent être ne importe quel réel ou nombre complexe , ou même un tout autre genre d'objet mathématique; voir le définition formelle ci-dessous .
Propriétés
Plus simplement, les fonctions exponentielles se multiplient à une vitesse constante. Par exemple, la population d'une culture bactérienne qui double tous les 20 minutes peut (approximativement, que ce ne est pas vraiment un problème continu) être exprimée comme une exponentielle, tout comme la valeur d'une voiture qui diminue de 10% par année.
En utilisant le logarithme naturel, on peut définir des fonctions exponentielles plus générales. La fonction
défini pour tous a> 0 et tous les nombres réels x, on appelle la fonction exponentielle avec la base a. A noter que cette définition de 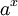 repose sur l'existence préalablement établie de la fonction
repose sur l'existence préalablement établie de la fonction 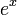 , Définie pour tous les nombres réels. (Ici, nous ne avons ni formellement, ni conceptuellement préciser si une telle fonction existe ou ce que les exposants non-naturelles sont censé signifier.)
, Définie pour tous les nombres réels. (Ici, nous ne avons ni formellement, ni conceptuellement préciser si une telle fonction existe ou ce que les exposants non-naturelles sont censé signifier.)
Notez que l'équation ci-dessus est valable pour a = e, puisque
Fonctions exponentielles "traduisent entre l'addition et la multiplication" comme il est exprimé dans les trois premiers et le cinquième des lois exponentielles suivantes:
Ce sont valables pour tous positifs nombres réels a et b, et tous les nombres x et y réel. Expressions impliquant des fractions et racines peuvent souvent être simplifiées en utilisant la notation exponentielle:
et, pour tout a> 0, nombre réel b, et un entier n> 1:
Dérivés et les équations différentielles
L'importance des fonctions exponentielles en mathématiques et les sciences se explique principalement par la propriété de leurs dérivés . En particulier,
Ce est, e x est son propre dérivé . Fonctions de la forme 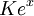 pour la constante K sont les seules fonctions avec cette propriété. (Cela découle du Théorème de Cauchy-Lipschitz, avec
pour la constante K sont les seules fonctions avec cette propriété. (Cela découle du Théorème de Cauchy-Lipschitz, avec 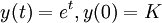 et
et 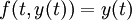 .) D'autres façons de dire la même chose comprennent:
.) D'autres façons de dire la même chose comprennent:
- La pente de la courbe en tout point est la hauteur de la fonction à ce moment.
- Le taux d'augmentation de la fonction au point x est égal à la valeur de la fonction en x.
- La fonction résout le équation différentielle
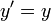 .
. - exp est un point fixe de dérivés, comme une fonctionnel
En fait, de nombreuses équations différentielles donnent naissance à des fonctions exponentielles, y compris la Équation et le Schrödinger L'équation de Laplace ainsi que les équations pour mouvement harmonique simple.
Pour les fonctions exponentielles avec d'autres bases:
Ainsi, toute fonction exponentielle est un multiple constant de son dérivé.
Si le taux de croissance ou de décroissance d'une variable est proportionnelle à sa taille - comme ce est le cas de la croissance illimitée de la population (voir Catastrophe malthusienne), continûment composé intérêt ou désintégration radioactive - alors la variable peut être écrit comme une constante fois une fonction exponentielle du temps.
En outre, pour toute fonction différentiable f (x), on trouve, par le règle de la chaîne:
Définition formelle
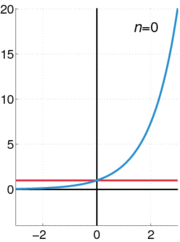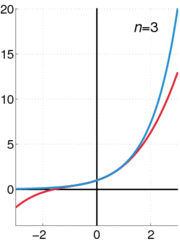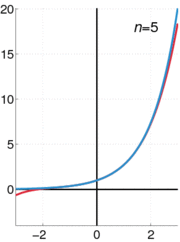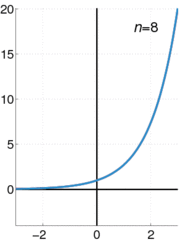
La fonction exponentielle e x peut être définie de différentes façons équivalentes, en tant que série infinie. En particulier, il peut être défini par une série de puissance :
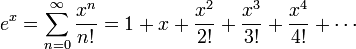 .
.
Notez que cette définition a la forme d'une série de Taylor . Utiliser une autre définition de la fonction exponentielle devrait conduire au même résultat lorsqu'il est déployé comme une série de Taylor .
Une définition moins commune définit 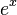 comme la solution
comme la solution 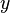 à l'équation
à l'équation
Valeur numérique
Pour obtenir la valeur numérique de la fonction exponentielle, la série infinie peut être réécrite comme:
Cette expression converger rapidement si nous pouvons nous assurer que x est inférieur à un.
Pour ce faire, nous pouvons utiliser l'identité suivante.
- Où
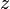 est la partie entière de
est la partie entière de 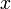
- Où
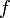 est la partie fractionnaire de
est la partie fractionnaire de 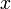
- De ce fait,
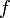 est toujours inférieur à 1 et
est toujours inférieur à 1 et 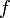 et
et 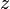 ajouter à
ajouter à 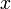 .
.
La valeur de la constante e z peut être calculée à l'avance en multipliant e z fois avec elle-même.
Informatique exp (x) pour x réel
Une meilleure algorithme peut être trouvé comme suit.
Tout d'abord, notez que la réponse y = e x est généralement un nombre à virgule flottante représenté par un mantisse m et un exposant n donc y = m 2 n pour un entier n et convenablement petite m. Ainsi, nous obtenons:
Prenant journal sur les deux côtés des deux dernière nous donne:
Ainsi, nous obtenons n que le résultat de la division de x par log (2) et de trouver le plus grand entier qui ne est pas supérieure à ce - ce est la fonction de chaussée:
Ayant trouvé n nous pouvons alors trouver la partie fractionnaire u comme ceci:
Le nombre u est petit et dans la gamme 0 ≤ u <ln (2) et ainsi nous pouvons utiliser la série mentionné précédemment pour calculer m:
Ayant constaté m et n nous pouvons produire ensuite y simplement en combinant ces deux en un nombre à virgule flottante:
Fractions continues pour e x
Via l'identité d'Euler:
Des techniques plus avancées sont nécessaires pour construire le suivant:
Réglage m = x et n = 2 rendements
Calcul du 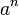 pour nombre naturel (entier positif) n
pour nombre naturel (entier positif) n
Il est un moyen rapide pour calculer 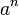 lorsque n est un entier positif. Il se sert du fait que les essais qu'un tel nombre est impair est très facile sur un ordinateur et en divisant par 2 est également rapide en déplaçant simplement tous les bits vers la droite.
lorsque n est un entier positif. Il se sert du fait que les essais qu'un tel nombre est impair est très facile sur un ordinateur et en divisant par 2 est également rapide en déplaçant simplement tous les bits vers la droite.
étape 1, initialiser certaines variables
y: = 1, k: = n, f: = a
étape 2, le test k
si k est 0, passez à l'étape 7
étape 3, (k ne est pas ici 0, test si k est pair)
si k est même aller à l'étape 5
étape 4, (k est impair ici, se multiplient dans) 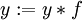
étape 5, (fracture de 2 k / ignore reste, diviser par quart de travail, f également carré)
k: k = décalage à droite par une f: f = f *
l'étape 6, (boucle)
retournez à l'étape 2
étape 7, (fait, y est un résultat = n)
y retourner
En C , vous pouvez écrire l'algorithme comme ceci:
alimentation double (double a, unsigned int n) {double-y = 1; à double f = a; unsigned int k = n; while (k = 0!) {if ((k & 1) = 0!) y * = f; >> k = 1; f = f *; } Return y; }alimentation double (double a, unsigned int n) {double-y = 1; à double f = a; unsigned int k = n; while (k = 0!) {if ((k & 1) = 0!) y * = f; >> k = 1; f = f *; } Return y; }
Alors que la multiplication d'un naïf ^ 100 100 exigerait itérations d'une boucle, cette multiplication d'une boucle itère seulement 7 fois (Le numéro 100 est écrit en utilisant sept bits).
Cet algorithme peut être facilement étendu pour les entiers signés par réaliser les étapes suivantes avant et après:
l'étape 1. Si k est négatif, nier la valeur de sorte que nous obtenons un positif k. n se souvient encore de la valeur d'origine.
étape 2. Effectuer le calcul ci-dessus pour 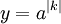
l'étape 3. Si n est négatif, inverser le résultat si y: = 1 / y. y est maintenant le résultat de 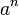 pour un nombre entier n.
pour un nombre entier n.
Sur le plan complexe
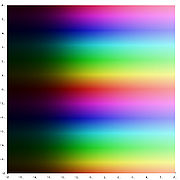
Comme dans la vraie cas, la fonction exponentielle peut être définie sur le plan complexe dans plusieurs formes équivalentes. Certaines de ces définitions miroir les formules pour la fonction exponentielle valeur réelle. Plus précisément, on peut encore utiliser la définition de la série de puissance, où la valeur réelle est remplacée par un complexe:
Selon cette définition, il est facile de montrer pourquoi 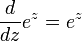 tient dans le plan complexe.
tient dans le plan complexe.
Une autre définition étend la réelle fonction exponentielle. Tout d'abord, nous déclarons la propriété désirée  . Pour
. Pour 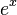 nous utilisons la réelle fonction exponentielle. Nous procédons ensuite en définissant seulement:
nous utilisons la réelle fonction exponentielle. Nous procédons ensuite en définissant seulement: 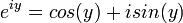 . Ainsi nous utilisons la réelle définition plutôt que de l'ignorer.
. Ainsi nous utilisons la réelle définition plutôt que de l'ignorer.
Considérée comme une fonction définie sur le plan complexe , la fonction exponentielle conserve les propriétés importantes
pour tout z et w.
C'est un fonction holomorphe qui est périodique période imaginaire 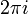 et peut être écrit comme
et peut être écrit comme
où a et b sont des valeurs réelles. Cette formule relie la fonction exponentielle avec les fonctions trigonométriques et de la fonctions hyperboliques. Ainsi, nous voyons que tous les fonctions élémentaires, sauf pour les polynômes jaillir de la fonction exponentielle d'une manière ou d'une autre.
Voir également La formule d'Euler.
Étendre le logarithme naturel à des arguments complexes donne une fonction multi-valeurs, ln (z). On peut alors définir une exponentiation plus général:
pour tous les nombres complexes z et w. Ce est aussi une fonction multi-valeurs. Les lois exponentielles ci-dessus indiquées restent vrai si interprété correctement que les déclarations sur les fonctions à valeurs multiples.
La fonction exponentielle cartes toute la ligne dans le plan complexe à un spirale logarithmique dans le plan complexe avec le centre à la origine. Deux cas particuliers peuvent être notées: lorsque la ligne d'origine est parallèle à l'axe réel, l'sprial résultant ne se referme sur elle-même; quand la ligne d'origine est parallèle à l'axe imaginaire, la spirale qui en résulte est un cercle d'un rayon quelconque.
- Lots de la fonction exponentielle sur le plan complexe
Calcul de exp (z) pour un complexe z
Ce est assez simple compte tenu de la formule
Notez que l'argument y pour les fonctions trigonométriques est réel.
Calcul du 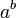 où a et b sont complexes
où a et b sont complexes
Ce est aussi simple étant donné les formules:
si a = x + yi et b = u + vi on peut convertir un premier à coordonnées polaires en trouvant un 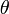 et un
et un  tel que:
tel que:
ou
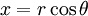 et
et 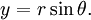
Ainsi, 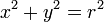 ou
ou 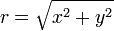 et
et 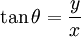 ou
ou 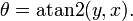
Maintenant, nous avons ce qui suit:
donc:
L'exposant est donc une simple multiplication de deux valeurs complexes produisant un résultat complexe qui peut ensuite être ramené au format cartésien régulier par la formule:
où p est la partie réelle de la multiplication:
et q est égal à la partie imaginaire de la multiplication:
Notez que toutes 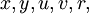
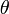 ,
, 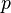 et
et 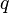 sont toutes les valeurs réelles dans ces calculs. Le résultat de
sont toutes les valeurs réelles dans ces calculs. Le résultat de 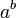 est donc
est donc 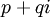 .
.
A noter également que depuis que nous calculons et l'utilisation 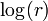 plutôt que de se r vous ne avez pas à calculer la racine carrée. Au lieu de simplement calculer
plutôt que de se r vous ne avez pas à calculer la racine carrée. Au lieu de simplement calculer 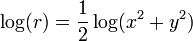 . Méfiez-vous des trop-plein potentiel si et éventuellement réduire le x et y avant informatique
. Méfiez-vous des trop-plein potentiel si et éventuellement réduire le x et y avant informatique 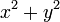 par une puissance de deux si approprié
par une puissance de deux si approprié 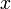 et
et 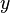 sont si grands que vous déborder. Si vous place courez le risque de débordement, l'échelle par une puissance convenable de deux avant de calculer la somme des carrés. Dans les deux cas, vous obtenez alors la version réduite de
sont si grands que vous déborder. Si vous place courez le risque de débordement, l'échelle par une puissance convenable de deux avant de calculer la somme des carrés. Dans les deux cas, vous obtenez alors la version réduite de 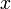 - Nous pouvons l'appeler
- Nous pouvons l'appeler 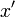 et la version réduite de
et la version réduite de 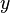 - Appelle
- Appelle 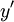 et ainsi vous obtenez:
et ainsi vous obtenez:
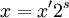 et
et 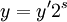
où 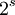 est le facteur d'échelle.
est le facteur d'échelle.
Ensuite, vous obtenez 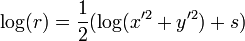 où
où 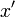 et
et 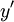 sont mis à l'échelle de sorte que la somme des carrés ne sera pas déborder ou négatif. Si
sont mis à l'échelle de sorte que la somme des carrés ne sera pas déborder ou négatif. Si 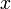 est très grand alors
est très grand alors 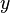 est très faible de sorte que vous ne pouvez pas trouver un tel facteur d'échelle vous déborder de toute façon et si la somme est sensiblement égale à
est très faible de sorte que vous ne pouvez pas trouver un tel facteur d'échelle vous déborder de toute façon et si la somme est sensiblement égale à 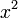 puisque y est ignorée et donc vous obtenez
puisque y est ignorée et donc vous obtenez 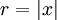 dans ce cas et
dans ce cas et 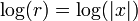 . La même chose arrive dans le cas où
. La même chose arrive dans le cas où 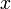 est très faible et
est très faible et 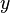 est très grande. Si les deux sont très grandes ou les deux sont très petites, vous pouvez trouver un facteur d'échelle tel que mentionné précédemment.
est très grande. Si les deux sont très grandes ou les deux sont très petites, vous pouvez trouver un facteur d'échelle tel que mentionné précédemment.
Notez que cette fonction est, en général, plusieurs valeurs pour les arguments complexes. Ce est parce que la rotation d'un seul point à travers ne importe quel angle, plus 360 degrés, ou 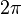 radians, est le même que l'angle de rotation à travers elle-même. Si
radians, est le même que l'angle de rotation à travers elle-même. Si 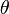 ci-dessus ne est pas unique:
ci-dessus ne est pas unique: 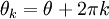 pour tout entier
pour tout entier 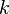 ferait ainsi. La convention est que, lorsque de
ferait ainsi. La convention est que, lorsque de  est pris comme une valeur unique, il doit être que, pour
est pris comme une valeur unique, il doit être que, pour 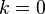 , Ie. nous utilisons la plus petite valeur possible (en amplitude) de thêta, qui a une amplitude, au plus,
, Ie. nous utilisons la plus petite valeur possible (en amplitude) de thêta, qui a une amplitude, au plus, 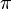 .
.
Matrices et algèbres de Banach
La définition de la fonction exponentielle donnée ci-dessus peut être utilisé pour chaque verbatim Algèbre de Banach, et en particulier pour carrés matrices (dans ce cas, la fonction est appelée la matrice exponentielle). Dans ce cas, nous avons
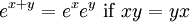
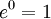
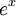 est inversible inverse
est inversible inverse 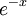
- le dérivé de
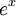 au point
au point 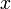 ce est que la carte linéaire qui envoie
ce est que la carte linéaire qui envoie 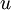 à
à 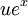 .
.
Dans le cadre des algèbres de Banach non-commutatives, comme algèbres de matrices ou des opérateurs sur Banach ou Espaces de Hilbert, la fonction exponentielle est souvent considérée comme une fonction d'un argument réel:
où A est un élément fixe de l'algèbre et t est un nombre réel. Cette fonction a les propriétés importantes
Sur les algèbres de Lie
Le exponentielle envoyant un Algèbre de Lie à la groupe de Lie qui a donné lieu à elle partage les propriétés ci-dessus, ce qui explique la terminologie. En fait, depuis R est l'algèbre de Lie du groupe de Lie de tous les nombres réels positifs avec la multiplication, la fonction exponentielle ordinaire pour de vrais arguments est un cas particulier de la situation d'algèbre de Lie. De même, depuis l'algèbre de Lie M (n, R) de l'ensemble des matrices réelles carrés appartient au groupe de Lie de toutes les matrices carrées inversibles, la fonction exponentielle pour les matrices carrées est un cas particulier de la carte exponentielle algèbre de Lie.
Double fonction exponentielle
La fonction exponentielle double terme peut avoir deux significations:
- une fonction avec deux termes exponentiels, avec différents exposants
- une fonction
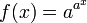 ; cette pousse encore plus vite que d'une fonction exponentielle; Par exemple, si a = 10: f (-1) = 1,26, f (0) = 10, f (1) = 10 10, f (2) = 10 100 = googol, ..., f (100) = googolplex.
; cette pousse encore plus vite que d'une fonction exponentielle; Par exemple, si a = 10: f (-1) = 1,26, f (0) = 10, f (1) = 10 10, f (2) = 10 100 = googol, ..., f (100) = googolplex.
Factorielles croissent plus vite que les fonctions exponentielles, mais plus lentement que les fonctions doubles-exponentielle. Nombres de Fermat, générés par 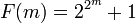 et numéros doubles de Mersenne générés par
et numéros doubles de Mersenne générés par 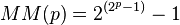 sont des exemples de fonctions exponentielles doubles.
sont des exemples de fonctions exponentielles doubles.
Propriétés similaires de  et la fonction
et la fonction 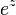
La fonction 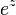 ne est pas dans C (z) (ie. pas le quotient de deux polynômes avec des coefficients complexes).
ne est pas dans C (z) (ie. pas le quotient de deux polynômes avec des coefficients complexes).
Pour les nombres complexes n distinctes 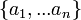 ,
, 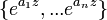 est linéairement indépendants sur C (z).
est linéairement indépendants sur C (z).
La fonction 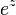 est transcendant sur C (z).
est transcendant sur C (z).
Périodicité
Pour tous les entiers n et x complexe:
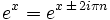
Preuve:

Pour tous les entiers positifs n et complexe a & x:
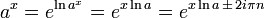

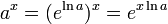
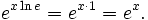
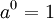
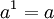
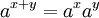
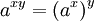
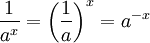
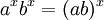
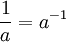
![\, \ Sqrt [n] {a ^ b} = \ left (\ sqrt [n] {a} \ right) ^ b = a ^ {b / n}.](../../images/90/9057.png)
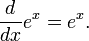
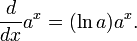
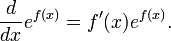
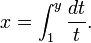
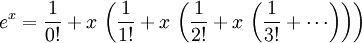
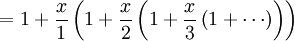
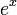
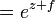
![\, = E ^ z \ times \ left [{1 \ over 0!} + F \, \ left ({1 \ over 1!} + F \, \ left ({1 \ over 2!} + F \, \ gauche ({1 \ over 3!} + \ cdots \ right) \ right) \ right) \ right]](../../images/90/9079.png)