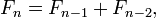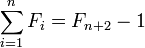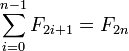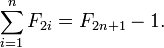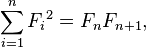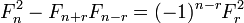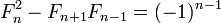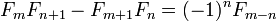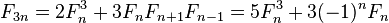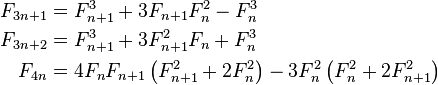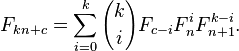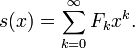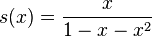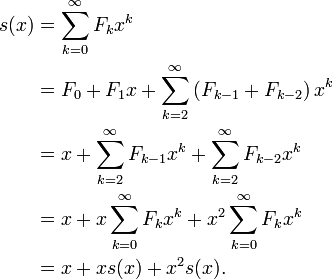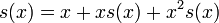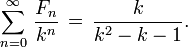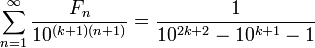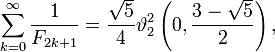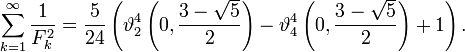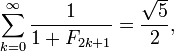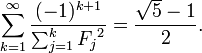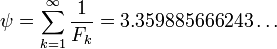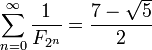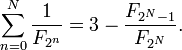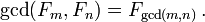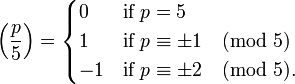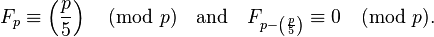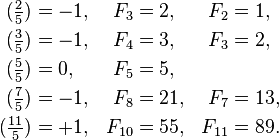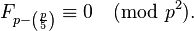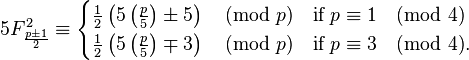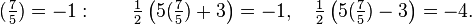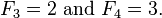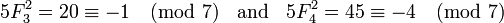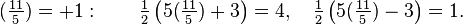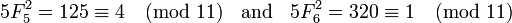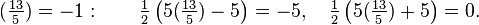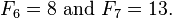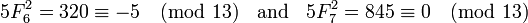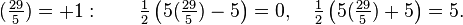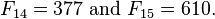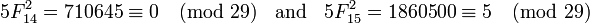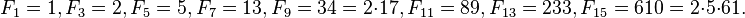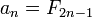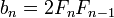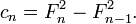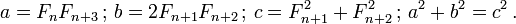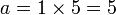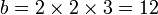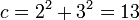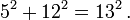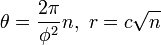Numéro Fibonacci
Saviez-vous ...
Cette sélection Wikipedia est déconnecté disponibles à partir enfants SOS pour la distribution dans le monde en développement. Avant de vous décider à propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur différents organismes de parrainage premier ?
En mathématiques , les nombres de Fibonacci ou séries de Fibonacci ou la séquence de Fibonacci sont les nombres dans la suite séquence entier:
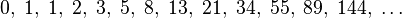 (Séquence A000045 dans OEIS )
(Séquence A000045 dans OEIS )
Par définition, les deux premiers nombres dans la suite de Fibonacci sont 0 et 1, et chaque nombre subséquent est la somme des deux précédents.
En termes mathématiques, la séquence F n des nombres de Fibonacci est définie par la relation de récurrence
avec des valeurs de semences
La suite de Fibonacci est nommé d'après Léonard de Pise, qui était connu comme Fibonacci. 1202 livre de Fibonacci Liber Abaci introduit la séquence aux mathématiques Europe de l'Ouest, bien que la séquence avait été décrit plus tôt dans les mathématiques indiennes . Par convention moderne, la séquence commence soit avec F 0 = 0 ou 1 F = 1. Le Liber Abaci a commencé la séquence avec F 1 = 1, sans le 0 initial.
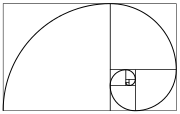
Nombres de Fibonacci sont étroitement liées à Numéros Lucas en ce qu'ils sont une paire complémentaire de Séquences Lucas. Ils sont intimement liés avec le nombre d'or ; par exemple, la les plus proches approximations rationnelles à le rapport sont 2/1, 3/2, 5/3, 8/5, .... Les applications comprennent des algorithmes informatiques tels que le Fibonacci technique de recherche et de la Structure de données de tas de Fibonacci, et les graphiques appelé cubes de Fibonacci utilisés pour l'interconnexion des systèmes parallèles et distribués. Ils apparaissent également dans les paramètres biologiques, tels que la ramification dans les arbres, phyllotaxie (la disposition des feuilles sur une tige), les germes de fruits d'un ananas, la floraison de artichaut, un défrisage fougère et la disposition d'un cône de pin.
Origines

La séquence de Fibonacci apparaît dans les mathématiques indiennes , dans le cadre de Chandas. Dans la tradition orale sanscrit, il y avait beaucoup d'accent sur la durée (L) syllabes se mélangent avec le court (S), et en comptant les différents modèles de L et S au bout de résultats donnés de longueur fixe dans les nombres de Fibonacci; le nombre de motifs qui sont courtes syllabes m est le nombre de Fibonacci de temps F m + 1.
Susantha Goonatilake écrit que le développement de la suite de Fibonacci "est attribuée en partie à Pingala (200 avant JC), étant associé plus tard Virahanka (c. 700 AD), Gopala (c. 1135), et Hemachandra (c. 1150) ". Parmanand Singh cite cryptique cha formule misrau de Pingala (" les deux sont mélangés ") et cite les chercheurs qui l'interprètent dans leur contexte comme disant que les cas pour m temps (F m + 1) est obtenu en ajoutant un [S] pour F M cas et [L] pour les m -1 cas F Il dates Pingala. avant 450 BCE.
Cependant, la plus claire exposition de la série se pose dans le travail de Virahanka (c. 700 de notre ère), dont le travail est perdu, mais il est disponible dans une citation de Gopala (c 1135.):
- Variations de deux mètres antérieures [est la variation] ... Par exemple, pour [un mètre de longueur] quatre, les variations de mètres de deux [et] étant mélangé trois, cinq se produit. [Travaux des exemples 8, 13, 21] ... De cette façon, le processus devrait être suivie dans tous les Matra-vṛttas [combinaisons] prosodiques.
La série est également discuté par Gopala (avant 1135 AD) et par le savant Jain Hemachandra (c. 1150).
Dans l'Ouest, la séquence de Fibonacci apparaît d'abord dans le livre Liber Abaci (1202) de Léonard de Pise, connue sous le nom Fibonacci. Fibonacci considère la croissance d'une idéalisée (biologiquement irréaliste) de lapin population, en supposant que: une paire de lapins nouveau-né, un mâle, une femelle, sont mis dans un champ; lapins sont capables de se accoupler à l'âge de un mois de sorte qu'à la fin de son deuxième mois une femelle peut produire une autre paire de lapins; lapins ne meurent jamais et une paire d'accouplement produit toujours une nouvelle paire (un homme et une femme) chaque mois à partir du deuxième mois de suite. Le puzzle qui Fibonacci posée était: combien de paires qu'il y aura dans un an?
- A la fin du premier mois, ils se accouplent, mais il ya encore seulement une paire.
- À la fin du deuxième mois de la femelle produit une nouvelle paire, alors maintenant il ya deux paires de lapins dans le domaine.
- A la fin du troisième mois, la femelle initial produit une deuxième paire, ce qui dans tous les trois paires sur le terrain.
- À la fin du quatrième mois, la femelle originale a produit encore une autre nouvelle paire, la femelle né il ya deux mois produit sa première paire également, faisant cinq paires.
A la fin de la n ème mois, le nombre de paires de lapins est égal au nombre de nouveaux couples (qui est le nombre de paires dans le mois n - 2) plus le nombre de couples vivant dernier mois (n - 1). Ce est la n-ième nombre de Fibonacci.
Le nom "séquence de Fibonacci" a été d'abord utilisé par le nombre théoricien du 19ème siècle Édouard Lucas.
Liste des nombres de Fibonacci
Le premier 21 nombre de Fibonacci F n pour n = 0, 1, 2, ..., 20 sont les suivants:
F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11 F 12 F 13 F 14 F 15 F 16 F 17 F 18 F 19 F 20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765
La séquence peut également être étendu à indice négatif n utilisant la relation de récurrence réarrangée
ce qui donne la séquence des numéros de "satisfaisant" negafibonacci
Ainsi, la séquence est bidirectionnelle
F -8 F -7 F -6 F -5 F -4 F -3 F -2 F -1 F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 -21 13 -8 5 -3 2 -1 1 0 1 1 2 3 5 8 13 21
Événements en mathématiques

Les nombres de Fibonacci se produisent dans les sommes d'diagonales "peu profondes» dans le triangle de Pascal (voir coefficient binomial ).
Les nombres de Fibonacci peuvent être trouvés dans différentes manières dans la séquence de binaires cordes.
- Le nombre de chaînes binaires de longueur n 1 consécutifs sans est le nombre de Fibonacci F n 2. Par exemple, sur les 16 chaînes binaires de longueur 4, il ya F 6 = 8 sans 1 consécutifs - ils sont 0000, 0100, 0010, 0001, 0101, 1000, 1010 et 1001. Par symétrie, le nombre de chaînes de longueur n est 0 consécutifs sans également F 2 n.
- Le nombre de chaînes binaires de longueur n sans un nombre impair de 1 consécutifs est le nombre de Fibonacci F n + 1. Par exemple, sur les 16 chaînes binaires de longueur 4, il ya F 5 = 5 sans un nombre impair de 1 consécutifs - ils sont 0000, 0011, 0110, 1100, 1111.
- Le nombre de chaînes binaires de longueur n sans un nombre pair de 0 ou 1 consécutifs est 2 F n. Par exemple, sur les 16 chaînes binaires de longueur 4, il ya 2 F 4 = 6 sans un nombre pair de 0 ou 1 consécutifs - ils sont 0001, 1000, 1110, 0111, 0101, 1010.
Rapport au nombre d'or
Solution de forme fermée
Comme chaque séquence définie par un récurrence linéaire à coefficients constants, les nombres de Fibonacci ont une solution de forme fermée. Il est devenu connu sous le nom La formule de Binet, même si elle était déjà connue par Abraham de Moivre:
où
est le nombre d'or (séquence A001622 dans OEIS ), et
Pour le voir, notons que φ et ψ sont deux solutions des équations
de sorte que les pouvoirs de φ et ψ satisfont la récurrence de Fibonacci. Autrement dit
et
Il se ensuit que, pour toutes les valeurs a et b, la séquence définie par
satisfait même récidive
Si A et B sont choisis de telle sorte que U 0 = 0 et U 1 = 1 alors la séquence résultante U n doit être la suite de Fibonacci. Ce est le même comme exigeant a et b satisfaire le système d'équations:
solution qui a
la production de la formule requise.
Calcul en arrondissant
Depuis
pour tout n ≥ 0, le nombre F n est le nombre entier le plus proche de
Par conséquent, il peut être trouvé par arrondissement, ou en termes de fonction de chaussée:
Ou la fonction entier le plus proche:
De même, si nous savons déjà que le nombre F> 1 est un nombre de Fibonacci, nous pouvons déterminer son indice dans la séquence par
Limite de quotients consécutifs
Johannes Kepler observe que le rapport des nombres de Fibonacci consécutifs converge. Il a écrit que «5 à 8 est donc est de 8 à 13, dans la pratique, et comme 8 est à 13, est donc de 13 à 21 presque", et a conclu que la limite se approche le rapport φ or.
Cette convergence ne dépend pas des valeurs initiales choisies, à l'exclusion de 0, 0. Par exemple, les valeurs initiales 19 et 31 génèrent la séquence 19, 31, 50, 81, 131, 212, 343, 555 ... etc. Le rapport de mandats consécutifs de cette séquence montre la même convergence vers le nombre d'or.
En fait, ce est valable pour ne importe quelle séquence qui satisfait à la réapparition de Fibonacci autre qu'une séquence de 0 ce. Cela peut être dérivée de la formule de Binet .
Une autre conséquence est que la limite du rapport de deux nombres de Fibonacci compensée par un écart d'indice fini particulier correspond au nombre d'or soulevée par cette déviation. Ou, en d'autres termes:
Décomposition des pouvoirs du nombre d'or
Étant donné que le nombre d'or satisfait à l'équation
Cette expression peut être utilisée pour décomposer des puissances supérieures φ n comme une fonction linéaire de puissances inférieures, qui à son tour peut être décomposé tout en bas à une combinaison linéaire de φ et 1. La résultante relations de récurrence donnent les nombres de Fibonacci que les coefficients linéaires:
Cette équation peut être prouvé par récurrence sur n.
Cette expression est également vrai pour n <1 si la séquence de Fibonacci F n est étendu aux entiers négatifs en utilisant la règle de Fibonacci 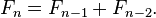
forme matricielle
Un système de deux dimensions linéaire équations aux différences qui décrit la suite de Fibonacci est
Les valeurs propres de la matrice A sont 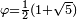 et
et 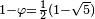 Et les éléments des vecteurs propres de A,
Et les éléments des vecteurs propres de A, 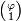 et
et 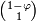 , Sont dans les ratios φ et φ-1 L'utilisation de ces faits, et les propriétés des valeurs propres, nous pouvons tirer une formule directe pour la n-ième élément de la série de Fibonacci comme un fonction analytique de n:
, Sont dans les ratios φ et φ-1 L'utilisation de ces faits, et les propriétés des valeurs propres, nous pouvons tirer une formule directe pour la n-ième élément de la série de Fibonacci comme un fonction analytique de n:
La matrice a un facteur de -1, et par conséquent ce est un 2 × 2 matrice unimodulaire. Cette propriété peut être compris en termes de continué la représentation de la fraction du nombre d'or:
Les nombres de Fibonacci se produire comme le rapport entre convergents successifs de la fraction continue de φ, et la matrice formée à partir de ne importe quel convergents successifs de fraction continue a un facteur de 1 ou -1.
La représentation de la matrice donne la suivante expression fermé pour les nombres de Fibonacci:
Prenant le déterminant des deux côtés de cette équation rendements L'identité de Cassini
En outre, étant donné que 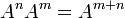 pour toute matrice carrée A, les identités suivantes peuvent être dérivées:
pour toute matrice carrée A, les identités suivantes peuvent être dérivées:
En particulier, avec m = n,
Ces deux dernières identités fournissent un moyen de calculer les nombres de Fibonacci de manière récursive en O (log (n)) opérations arithmétiques et en temps O (M (n) log (n)), où M (n) est le temps pour la multplication de deux nombres de n chiffres. Cela correspond à l'heure de calcul de la n-ième nombre de Fibonacci de la formule de matrice de forme fermée, mais avec moins d'étapes redondantes si l'on évite de recalculer un déjà calculé nombres de Fibonacci (de récurrence avec mémorisation).
Reconnaissant les nombres de Fibonacci
La question peut se poser de savoir si un nombre entier positif z est un nombre de Fibonacci. Etant donné que F (n) est le nombre entier le plus proche de 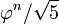 , Test de force brute la plus simple est l'identité
, Test de force brute la plus simple est l'identité
ce qui est vrai si et seulement si z est un nombre de Fibonacci. Dans cette formule, F (n) peut être calculé en utilisant rapidement l'une des forme fermée expressions précédemment.
Une des conséquences de l'expression ci-dessus est le suivant: si l'on sait qu'un certain nombre z est un nombre de Fibonacci, on peut déterminer un n tel que F (n) = z par ce qui suit:
En variante, un nombre entier positif z est un nombre de Fibonacci si et seulement si l'une des 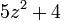 ou
ou 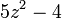 est un carré parfait.
est un carré parfait.
Un test peu plus sophistiqué utilise le fait que la convergents de la continué représentation fraction de φ sont des rapports de nombres de Fibonacci successifs. Autrement dit, l'inégalité
(Avec coprime entiers positifs p, q) est vrai si et seulement si p et q sont des nombres de Fibonacci successifs. Du même une dérive du critère selon lequel z est un nombre de Fibonacci si et seulement si le intervalle fermé
contient un nombre entier positif. Pour z ≥ 2, il est facile de montrer que cet intervalle contient au plus un nombre entier, et dans le cas où z est un nombre de Fibonacci, le contenu entier est égal au nombre de Fibonacci successifs après z. Assez remarquablement, ce résultat tient toujours pour le cas z = 1, mais il doit être déclaré attentivement depuis le 1er apparaît deux fois dans la suite de Fibonacci, et a donc deux successeurs distinctes.
Identités combinatoires
La plupart des identités des nombres de Fibonacci peuvent être prouvées à l'aide arguments combinatoires en utilisant le fait que F n peut être interprété comme le nombre de séquences de 1s et 2s cette somme à n - 1. Cela peut être considéré comme la définition de F n, avec la convention que F 0 = 0, ce qui signifie qu'aucune somme va ajouter jusqu'à -1, et que F 1 = 1, ce qui signifie la somme sera vide "ajouter" à 0. Voici l'ordre des questions de summand. Par exemple, 1 + 2 + 1 et 2 sont considérées comme deux sommes différentes.
Par exemple, la relation de récurrence
ou des mots, la n-ième nombre de Fibonacci est la somme des deux nombres de Fibonacci précédentes, peut être représentée en divisant le f (n) des sommes de 1s et 2s qui ajoutent à n -1 en deux groupes non chevauchants. Un groupe contient les sommes dont le mandat premier est une et l'autre de ces sommes dont le mandat premier est 2. Dans le premier groupe, les termes restants ajouter à n - 2, il a donc F (n -1) sommes, et dans le deuxième groupe les termes restants ajouter à n -3, donc il ya des sommes F (-2 n). Donc, il ya un total de F (n -1) + F n -2) sommes tout à fait, cette montre est égal à F (n).
De même, il peut être établi que la somme des nombres de Fibonacci première jusqu'à la n-ième est égale à la (n + 2) -ième nombre de Fibonacci moins 1. Dans symboles:
Cela se fait en divisant les sommes d'addition à n + 1 d'une manière différente, cette fois par l'emplacement de la première 2. Plus précisément, le premier groupe se compose de ces montants qui commencent par 2, le deuxième groupe ceux qui commencent 1 + 2 , la troisième 1 + 1 + 2, et ainsi de suite, jusqu'à ce que le dernier groupe qui se compose de la somme simple où seules de 1 sont utilisés. Le nombre de montants dans le premier groupe est F (n), F (n - 1) dans le second groupe, et ainsi de suite, avec une somme dans le dernier groupe. Ainsi, le nombre total des sommes est F (n) + F (n-1) + ... + F (1) 1 et donc cette quantité est égale à F (n 2)
Un argument similaire, regroupant les sommes par la position de la première 1 plutôt que le premier deux, donne deux autres identités:
et
En mots, la somme des premiers nombres de Fibonacci avec un indice impair jusqu'à F 2 n -1 est le (2n) ième nombre de Fibonacci, et la somme des premiers nombres de Fibonacci avec encore indexer jusqu'à 2 F n est la (2n + 1) -St nombre Fibonacci moins 1.
Un truc différent peut être utilisé pour prouver
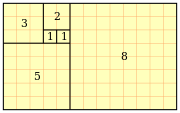
ou des mots, la somme des carrés des premiers nombres de Fibonacci jusqu'à F n est le produit de la n-ième et (n + 1) -ième nombres de Fibonacci. Dans ce cas, la note que Fibonacci rectangle de taille F n F (n + 1) peut être décomposé en carrés de taille F n, F n-1, et ainsi de suite pour F 1 = 1, d'où se ensuit l'identité par des zones de comparaison .
D'autres identités
Il existe de nombreuses autres identités qui peuvent être dérivées en utilisant diverses méthodes. Parmi les plus remarquables sont:
Catalan de l'identité:
Cassini de l'identité:
l'identité d'Ocagne:
où L n est la n ième Nombre Lucas. La dernière est une identité pour doubler n; d'autres identités de ce type sont
par l'identité de Cassini.
Ceux-ci peuvent être trouvées expérimentalement en utilisant réduction de treillis, et sont utiles dans la mise en place du tamis spéciale de champ numérique pour factoriser un nombre de Fibonacci.
Plus généralement,
Mettre k = 2 dans cette formule, on obtient à nouveau les formules de la fin de la section ci-dessus sous forme de matrice .
série Power
Le fonction génératrice de la suite de Fibonacci est la série de puissance
Cette série est convergente pour 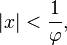 et sa somme a une forme fermée simple:
et sa somme a une forme fermée simple:
Ceci peut être prouvé en utilisant la récurrence de Fibonacci à étendre chaque coefficient dans la somme infinie:
Résoudre l'équation
S (x) les résultats ci-dessus dans la forme fermée.
Si x est l'inverse d'un nombre entier, la forme fermée de la série devient
En particulier,
pour tous les entiers non-négatifs k.
Certains mathématiques puzzle livres présente aussi curieux la valeur particulière 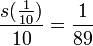 .
.
Sommes réciproques
Sommes infinies plus de nombres de Fibonacci réciproques peuvent parfois être évalués en termes de fonctions thêta. Par exemple, nous pouvons écrire la somme de tous les nombres de Fibonacci réciproque impair répertorié
et la somme des nombres de Fibonacci au carré comme réciproques
Si l'on ajoute 1 à chaque nombre de Fibonacci dans la première somme, il ya aussi la forme fermée
et il ya une belle somme imbriquée de nombres de Fibonacci carrés donnant l'inverse de la proportion dorée ,
De tels résultats font plausible qu'une formule fermée pour la somme plaine de nombres de Fibonacci réciproques n'a pu être trouvée, mais aucun ne est encore connu. Malgré cela, le réciproque constante Fibonacci
a été prouvé irrationnelle par Richard André-Jeannin.
Millin série donne une identité remarquable:
qui résulte de la forme fermée pour ses sommes partielles comme N tend vers l'infini:
Primes et la divisibilité
propriétés de divisibilité
Chaque troisième numéro de séquence est le même et, plus généralement, chaque k-ième numéro de la séquence est un multiple de k F. Ainsi, la suite de Fibonacci est un exemple d'un séquence de la divisibilité. En fait, la séquence de Fibonacci satisfait la propriété de divisibilité fort
nombres premiers de Fibonacci
Un premier Fibonacci est un nombre de Fibonacci qui est privilégié . La première quelques-uns sont:
- 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ... (séquence A005478 dans OEIS ).
Fibonacci amorce avec des milliers de chiffres ont été trouvés, mais on ne sait pas se il existe une infinité de nombres.
F kn est divisible par n F, de sorte que, en dehors de F 4 = 3, ne importe quel premier Fibonacci doit avoir un indice prime. Comme il ya arbitrairement longues séries de nombres composés, il ya donc aussi arbitrairement longues séries de nombres de Fibonacci composites.
A l'exception de 1, 8 et 144 (F 1 = F 2, F 6, F 12) chaque nombre de Fibonacci a un facteur premier qui ne est pas un facteur d'un nombre plus petit de Fibonacci ( Le théorème de Carmichael).
Le seul non triviale carré nombre Fibonacci est 144. Attila Pethő prouvé en 2001 qu'il n'y a qu'un nombre fini de nombres de Fibonacci puissance parfaites. En 2006, Y. Bugeaud, M. Mignotte, et S. Siksek prouvé que 8 et 144 sont les seuls de tels pouvoirs parfaits non triviales.
Aucun numéro de Fibonacci supérieure à F 6 = 8 est une plus ou un de moins que un nombre premier.
Les trois nombres de Fibonacci consécutifs, prises deux à la fois, sont relativement premier, ce est-
- pgcd (F n, F n 1) = pgcd (F n, F n 2) = 1.
Plus généralement,
- pgcd (F n, F m) = F pgcd (n, m).
Diviseurs premiers de nombres de Fibonacci
La divisibilité des nombres de Fibonacci par un nombre premier p est liée à la Symbole de Legendre 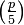 qui est évalué comme suit:
qui est évalué comme suit:
Si p est un nombre premier, alors
Par exemple,
On ne sait pas se il existe un nombre premier p tel que
Ces nombres premiers (si il y en a) seront appelés Wall-Sun-Sun amorce.
En outre, si p ≠ 5 est un nombre premier impair alors:
Exemple 1. p = 7, en l'occurrence p ≡ 3 (mod 4), et on a:
Exemple 2. p = 11, dans ce cas p ≡ 3 (mod 4), et on a:
Exemple 3. p = 13, dans ce cas p ≡ 1 (mod 4), et on a:
Exemple 4. p = 29, dans ce cas p ≡ 1 (mod 4), et on a:
Pour impair n, toutes les diviseurs premiers impairs de F n à 1 sont congruents modulo 4, ce qui implique que tous les diviseurs impairs de F n (comme les produits de diviseurs premiers impairs) sont congruents modulo 1 à 4.
Par exemple,
Tous les facteurs connus de Fibonacci numéros F (i) pour tout i <50000 sont recueillies à des référentiels pertinents.
Périodicité modulo n
On peut voir que, si les membres de la suite de Fibonacci sont prises mod n, la séquence résultante doit être périodique de période au plus n 2 -1. Les longueurs des périodes différentes pour n forment ce qu'on appelle Périodes Pisano (séquence A001175 dans OEIS ). La détermination des périodes Pisano est en général un problème ouvert, bien que pour tout n particulier, il peut être résolu comme une instance de détection de cycle.
Triangles rectangles
À partir de 5, chaque second nombre de Fibonacci est la longueur de l'hypoténuse d'un triangle rectangle dont les côtés sont des nombres entiers, ou en d'autres termes, le plus grand nombre dans un Triplet pythagoricien. La longueur de la branche la plus longue de ce triangle est égale à la somme des trois côtés du triangle précédentes, dans cette série de triangles, et la branche la plus courte est égale à la différence entre le nombre de Fibonacci précédentes contourné et la jambe plus courte de ce qui précède triangle.
Le premier triangle dans cette série a des côtés de longueur 5, 4 et 3. Sauter 8, la prochaine triangle a des côtés de longueur 13, 12 (5 + 4 + 3), et 5 (8-3). Saut 21, la prochaine triangle a des côtés de longueur 34, 30 (13 + 12 + 5), et 16 (21-5). Cette série se poursuit indéfiniment. Les côtés du triangle a, b, c peuvent être calculés directement à:
Ces formules répondent 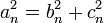 pour tout n, mais ils ne représentent qu'une côtés du triangle lorsque n> 2.
pour tout n, mais ils ne représentent qu'une côtés du triangle lorsque n> 2.
Tous les quatre nombres de Fibonacci consécutifs F n, F n + 1, F 2 et F n n 3 peut également être utilisé pour générer un triplet de Pythagore d'une manière différente:
Exemple 1: laissez les nombres de Fibonacci être 1, 2, 3 et 5. Puis:
Ampleur
Etant donné que F n est à asymptotique 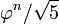 , Le nombre de chiffres par F n est asymptotique à
, Le nombre de chiffres par F n est asymptotique à 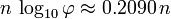 . En conséquence, pour tout entier d> 1 il ya 4 ou 5 avec des nombres de Fibonacci d chiffres décimaux.
. En conséquence, pour tout entier d> 1 il ya 4 ou 5 avec des nombres de Fibonacci d chiffres décimaux.
Plus généralement, dans la représentation de base b, le nombre de chiffres par F n est asymptotique à 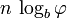 .
.
Applications
Les nombres de Fibonacci sont importantes dans le calcul l'analyse d'exécution de L'algorithme d'Euclide pour déterminer le plus grand commun diviseur de deux entiers: le pire cas pour l'entrée de cet algorithme est une paire de nombres de Fibonacci consécutifs.
Yuri Matiyasevich a pu montrer que les nombres de Fibonacci peuvent être définies par un Diophantienne équation, qui a conduit à sa solution originale de Dixième problème de Hilbert.
Les nombres de Fibonacci sont également un exemple d'un séquence complète. Cela signifie que chaque entier positif peut être écrit comme une somme de nombres de Fibonacci, où un seul numéro est utilisé qu'une seule fois au plus. Plus précisément, chaque entier positif peut être écrit de manière unique comme étant la somme d'un ou plusieurs nombres de Fibonacci distincts de telle manière que la somme ne comprend pas deux nombres de Fibonacci consécutifs tout. Ceci est connu comme Théorème de Zeckendorf, et une somme de nombres de Fibonacci qui répond à ces conditions est appelé une représentation Zeckendorf. La représentation Zeckendorf d'un certain nombre peut être utilisé pour tirer son Codage de Fibonacci.
Nombres de Fibonacci sont utilisés par certains des générateurs de nombres pseudo-aléatoire.
Les nombres de Fibonacci sont utilisés dans une version de la polyphasé fusionner algorithme de tri dans lequel une liste non triés est divisée en deux listes dont les longueurs correspondent aux nombres de Fibonacci séquentiel - en divisant la liste de sorte que les deux parties ont des longueurs dans la proportion φ approximative. Une mise en œuvre de lecteur de bande de la polyphasé tri par fusion a été décrit dans L'Art de la programmation informatique.
Les nombres de Fibonacci se posent dans l'analyse de la La structure de données en tas de Fibonacci.
Le Est un cube de Fibonacci graphe non orienté avec un nombre de Fibonacci de noeuds qui a été proposée comme un topologie de réseau pour calcul parallèle.
Procédé d'optimisation à une dimension, appelé le Fibonacci technique de recherche, utilise les nombres de Fibonacci.
La série de nombres de Fibonacci est utilisé pour option compression avec perte dans le IFF 8SVX format de fichier audio utilisé sur Ordinateurs Amiga. La série de numéros compands l'onde audio d'origine similaire aux méthodes logarithmiques telles que μ-loi.
Depuis la facteur de conversion des miles à 1.609344 kilomètres est proche du rapport d'or (φ notée), la décomposition de la distance en miles en une somme de nombres de Fibonacci devient presque la somme de kilomètres lorsque les nombres de Fibonacci sont remplacés par leurs successeurs. Cette méthode revient à une radix numéro 2 se inscrire à or φ de base de rapport étant décalé. Pour convertir des kilomètres en miles, décaler le registre bas de la suite de Fibonacci à la place.
Dans la nature
Séquences de Fibonacci apparaissent dans les paramètres biologiques, dans deux nombres de Fibonacci consécutifs, comme ramification dans les arbres, disposition des feuilles sur une tige, les petits fruits d'un ananas, la floraison de artichaut, une fougère défrisage et l'agencement d'un cône de pin. En outre, de nombreuses réclamations mal fondées de nombres de Fibonacci ou sections d'or dans la nature se trouvent dans les sources populaires, par exemple, relatives à l'élevage de lapins en propre exemple irréaliste de Fibonacci, les graines sur un tournesol, les spirales de coquillages, et la courbe de vagues. Les nombres de Fibonacci sont également présents dans l'arbre de la famille des abeilles.
Przemysław Prusinkiewicz a avancé l'idée que les cas réels peuvent en partie être compris comme l'expression de certaines contraintes algébriques sur groupes libres, en particulier que certains Grammaires Lindenmayer.
Un modèle pour le modèle de fleurons dans la tête d'un tournesol a été proposée par H. Vogel en 1979. Ce est de la forme
où n est le numéro d'index de la fleur et c est un facteur d'échelle constant; les fleurons se trouvent donc sur la spirale de Fermat. L'angle de divergence, d'environ 137,51 °, est l' angle d'or, divisant le cercle dans le nombre d'or. Parce que ce ratio est irrationnel, pas fleuron a un voisin exactement au même angle du centre, de sorte que les fleurons emballer efficacement. Parce que les approximations rationnelles à la proportion dorée sont de la forme F ( j ): F ( j + 1), les plus proches voisins de numéro de fleuron n sont ceux au n ± F ( j ) pour un indice j qui dépend de r , la la distance du centre. Il est souvent dit que les tournesols et les arrangements similaires ont 55 spirales dans un sens et 89 dans l'autre (ou d'une autre paire de nombres de Fibonacci adjacentes), mais c'est vrai que d'un éventail de rayons, généralement le plus à l'extérieur et donc plus visible.
Le code de l'ascendance d'abeille
nombres de Fibonacci apparaissent également dans la description de la reproduction d'une population d'abeilles idéalisées, selon les règles suivantes:
- Si un œuf est pondu par une femelle déconnectés, il élabore un mâle oubourdon abeille.
- Toutefois, si un oeuf est fertilisé par un mâle, une femelle l'éclosion.
Ainsi, une abeille mâle aura toujours un parent, et une abeille femelle aura deux.
Si l'on retrace l'origine de toute abeille mâle (1 d'abeille), il dispose de 1 parent (1 abeille), 2 grands-parents, grands-parents 3, 5 arrière-grands-parents, et ainsi de suite. Cette séquence de nombre de parents est la suite de Fibonacci. Le nombre d'ancêtres à chaque niveau, F n , est le nombre d'ancêtres féminins, qui est F n-1 , plus le nombre d'ancêtres mâles, qui est F n-2 . Ceci est dans l'hypothèse irréaliste que les ancêtres à chaque niveau sont par ailleurs sans rapport.
La culture populaire
Généralisations
La suite de Fibonacci a été généralisé à de nombreux égards. Ceux-ci comprennent:
- Généraliser l'index entiers négatifs pour produire lesNegafibonaccinuméros.
- Généraliser l'indice à des nombres réels en utilisant une modification de la formule de Binet.
- A partir des nombres entiers avec les autres.nombres Lucas ontL 1= 1,L 2= 3, etLn=L n-1+L n-2.Primefree séquences utilisent la récurrence de Fibonacci avec d'autres points de départ afin de générer des séquences dans lesquelles tous les chiffres sontcomposite.
- Laisser un nombre être une fonction linéaire (autre que la somme) des deux nombres précédents. Le Pell numéros ontPn= 2P n- 1+P n- 2.
- Sans adjonction des numéros précédents. Le Padovan séquence etles numéros ont PerrinP(n) =P(n- 2) +P(n- 3).
- Génération du prochain numéro en ajoutant 3 numéros (numéros de tribonacci), 4 numéros (numéros de tetranacci), ou plus. Les séquences résultantes sont connus comme n-Step nombres de Fibonacci .
- Ajout d'autres objets que des nombres entiers, par exemple des fonctions ou des chaînes-un exemple essentiel estpolynômes de Fibonacci.


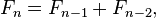
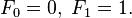
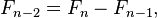
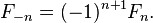
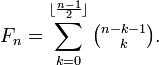
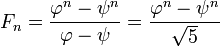
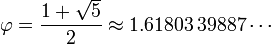
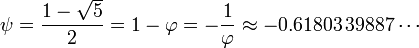
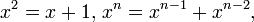
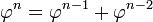
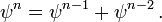
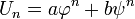
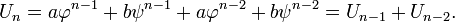
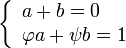
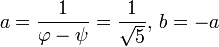
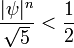
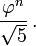
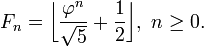
![F_n = \ bigg [\ frac {\ varphi ^ n} {\ sqrt 5} \ bigg], \ n \ geq 0.](../../images/2741/274107.png)
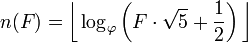
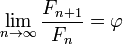
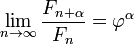
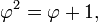
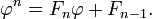
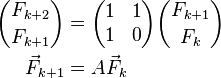
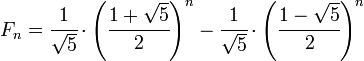
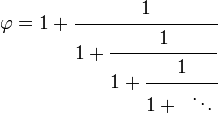
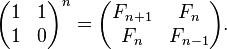
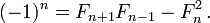
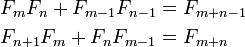
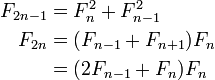
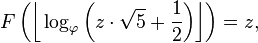
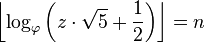
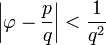
![\ Bigg [\ varphi z \ frac {1} {z}, \ varphi z + \ frac {1} {z} \ bigg]](../../images/2741/274132.png)