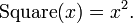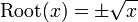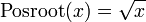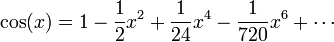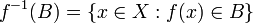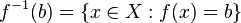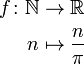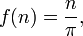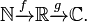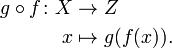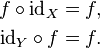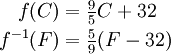Fonction (mathématiques)
Contexte des écoles Wikipédia
Cette sélection se fait pour les écoles par la charité pour enfants lire la suite . Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/
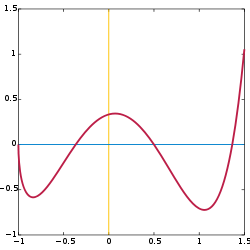
![\ Begin {align} et \ scriptstyle f \ colon [-1,1.5] \ à [-1,1.5] \\ & \ textstyle x \ mapsto \ frac {(4x ^ ^ 3-6x 2 + 1) \ sqrt { x + 1}} {3-x} \ end {align}](../../images/121/12113.png)
La mathématique notion de fonction exprime la dépendance entre deux grandeurs, dont l'une est indiquée (le variable indépendante, argument de la fonction, ou de son "entrée") et l'autre produit (la variable dépendante, la valeur de la fonction, ou "sortie"). Une fonction associe une seule sortie pour chaque élément d'entrée partant d'un fixe définir, tels que les nombres réels .
Il ya plusieurs façons de donner une fonction: par une formule , par une intrigue ou graphique, par un algorithme qui calcule ce, d'une description de ses propriétés. Parfois, une fonction est décrite à travers sa relation à d'autres fonctions (voir, par exemple, la fonction inverse ). Dans les disciplines appliquées, les fonctions sont souvent spécifiées par leurs tableaux de valeurs ou par une formule. Pas tous les types de la description peuvent être donnés pour chaque fonction possible, et il faut faire une distinction nette entre la fonction elle-même et plusieurs façons de présenter ou de le visualiser.
Une idée de grande importance dans l'ensemble des mathématiques est la composition de fonctions : si z est une fonction de y et y est une fonction de x, alors z est une fonction de x. On peut décrire de façon informelle en disant que la fonction composite est obtenu en utilisant la sortie de la première fonction en tant que l'entrée de la seconde. Cette fonctionnalité des fonctions les distingue des autres constructions mathématiques, comme les numéros ou chiffres, et fournit la théorie des fonctions avec sa structure la plus puissante.
Introduction
Fonctions jouent un rôle fondamental dans tous les domaines des mathématiques, ainsi que dans les autres sciences et de l'ingénierie. Cependant, l'intuition se rapportant à des fonctions, la notation, et même le sens même du terme «fonction» varie entre les champs. Plus de zones abstraites des mathématiques, comme la théorie des ensembles , considèrent types très généraux de fonctions, qui ne peuvent être spécifiées par une règle concrète et ne sont pas régis par des principes familiers. La propriété caractéristique d'une fonction dans le sens le plus abstrait est qu'elle concerne précisément une sortie à chacune de ses entrées admissibles. Ces fonctions ne implique pas nécessairement le nombre et peuvent, par exemple, associer chacun d'un ensemble de mots avec leurs propres premières lettres.
Fonctions dans l'algèbre sont généralement exprimable en termes de opérations algébriques. Fonctions étudiés dans l'analyse , comme la fonction exponentielle , peuvent avoir des propriétés supplémentaires résultant de la continuité de l'espace, mais dans le cas le plus général ne peuvent pas être défini par une formule unique. Fonctions analytiques dans analyse complexe peut être définie assez concrètement par leur développements en série. D'autre part, dans lambda-calcul, la fonction est un concept primitif, au lieu d'être défini en termes de la théorie des ensembles. Les termes transformation et cartographie sont souvent synonyme de fonction. Dans certains contextes, cependant, ils diffèrent légèrement. Dans le premier cas, la transformation terme se applique généralement aux fonctions dont les entrées et les sorties sont des éléments d'un même ensemble ou une structure plus générale. Ainsi, on parle de transformations linéaires d'un espace vectoriel dans lui-même et de symétrie transformations d'un objet géométrique ou un motif. Dans le second cas, utilisé pour décrire des ensembles dont la nature est arbitraire, la cartographie du terme est le concept le plus général de la fonction.
Les fonctions mathématiques sont souvent désignés par des lettres, et la notation standard pour la sortie d'une fonction ƒ avec l'entrée x est f (x). Une fonction peut être définie que pour certains intrants, et la collecte de toutes les entrées acceptables de la fonction est appelée son domaine. L'ensemble de toutes les sorties résultant est appelé gamme de la fonction. Cependant, dans de nombreux domaines, il est également important de préciser le codomain d'une fonction, qui contient la plage, mais ne est pas nécessairement égale. La distinction entre la plage et codomaine nous permet de se demander si les deux se trouvent être égales, ce qui dans certains cas peut être une question d'un certain intérêt mathématique.
Par exemple, l'expression de ƒ (x) = x 2 décrit une fonction f d'une variable x, qui, en fonction du contexte, peuvent être un nombre entier , un réel ou complexe même nombre ou un élément d'un groupe . Précisons que x est un entier; alors cette fonction concerne chaque entrée, x, avec une seule sortie, x 2, x obtenue à partir de quadrature. Ainsi, l'entrée 3 est reliée à la sortie 9, dont l'entrée 1 à la sortie 1, et l'entrée de -2 à la sortie 4, et on écrit ƒ (3) = 9, ƒ (1) = 1, ƒ (-2) = 4. Depuis tout entier peut être carré, le domaine de cette fonction se compose de tous les entiers, tandis que sa gamme est l'ensemble des carrés parfaits. Si nous choisissons entiers que le codomaine ainsi, nous constatons que de nombreux numéros, tels que 2, 3, et 6, sont dans l'ensemble d'arrivée mais non la gamme.
Ce est une pratique habituelle en mathématiques d'introduire des fonctions temporaires avec des noms comme ƒ; dans le paragraphe suivant nous pourrions définir ƒ (x) = 2 x 1, puis ƒ (3) = 7. Quand un nom pour la fonction ne est pas nécessaire, souvent la forme y = x 2 est utilisé.
Si nous utilisons une fonction souvent, nous pouvons lui donner un nom plus permanente comme, par exemple,
La propriété essentielle d'une fonction est que, pour chaque entrée, il doit y avoir une sortie unique. Ainsi, par exemple, la formule
ne définit pas une fonction d'une variable réelle positive, car elle attribue deux sorties à chaque numéro: les racines carrées de 9 sont 3 et -3. Pour rendre la racine carrée d'une fonction, il faut préciser ce qui racine carrée de choisir. La définition
pour toute entrée positive choisit la racine carrée positive comme une sortie.
Comme mentionné ci-dessus, une fonction ne implique pas nécessairement des nombres. A titre d'exemples, considérer la fonction qui associe à chaque mot sa première lettre ou la fonction qui associe à chaque triangle sa zone.
Définitions
Comme les fonctions sont utilisées dans de nombreux domaines des mathématiques, et de tant de manières différentes, pas de définition unique de la fonction a été universellement adoptée. Certaines définitions sont élémentaires, tandis que d'autres utilisent un langage technique qui peut obscurcir la notion intuitive. Néanmoins, l'idée essentielle est la même dans toute définition.
Une définition élémentaire est que
- Une fonction est donnée par une expression arithmétique décrivant comment une nombre dépend de l'autre.
Un exemple d'une telle fonction est y = 5 x 16 -20 x 3 x 5, où la valeur de y dépend de la valeur de x. Ce est tout à fait satisfaisante pour les parties des mathématiques élémentaires, mais est trop maladroit et restrictive pour les zones plus avancées. Par exemple, le cosinus fonction utilisée dans la trigonométrie ne peut pas être écrit de cette manière; le mieux que nous pouvons faire, ce est un série infinie,
Cela dit, si nous sommes prêts à accepter série comme un sens large de «expression arithmétique", nous avons une définition qui a servi mathématiques raisonnablement bien pendant des centaines d'années.
Finalement, la transformation progressive de "calcul" intuitive dans "analyse" formelle a la nécessité d'une définition plus large. L'accent se est déplacé de la façon dont une fonction a été présenté - comme une formule ou une règle - à un concept plus abstrait. Une partie de la nouvelle fondation était l'utilisation de jeux , de sorte que les fonctions ne sont plus limités aux numéros. Ainsi nous pouvons dire que
- Une fonction f d'un ensemble X à un ensemble Y associés à chaque élément x de X un élément y = f (x) dans Y.
Notez que X et Y ne doit pas nécessairement être différents ensembles; il est possible d'avoir une fonction d'un ensemble à lui-même. Bien qu'il soit possible d'interpréter le terme «associés» à cette définition avec une règle concrète pour l'association, il est essentiel d'aller au-delà de cette restriction. Par exemple, nous pouvons parfois prouver qu'une fonction de certaines propriétés existe, mais ne pas être en mesure de donner une règle explicite pour l'association. En fait, dans certains cas, il est impossible de donner une règle explicite y produire un spécifique pour chaque x, même si une telle fonction existe. Dans le cadre des fonctions définies sur des ensembles arbitraires, il ne est même pas clair comment l'expression "règle explicite" doit être interprétée.
Comme fonctions prennent de nouveaux rôles et de trouver de nouveaux usages, la relation de la fonction des ensembles nécessite plus de précision. Peut-être que chaque élément Y est associée à certains x, peut-être pas. Dans certaines parties des mathématiques, y compris la théorie et la récursivité analyse fonctionnelle, il est commode pour autoriser les valeurs de x sans association (dans ce cas, le terme fonction partielle est souvent utilisé). Pour être en mesure de discuter de telles distinctions, de nombreux auteurs répartis en fonction en trois parties, chacune un ensemble:
- Une fonction f est un triplet ordonné d'ensembles (F, X, Y) avec des restrictions, où
- F (graphique) est un ensemble de couples (x, y),
- X (la source) contient tous les premiers éléments de F et peut-être plus, et
- Y (la cible) contient tous les éléments du deuxième F et peut-être plus.
Les restrictions les plus courantes sont que F x paires chacun avec un seul y, et que X est simplement l'ensemble des premiers éléments de F et pas plus.
En l'absence de restrictions sont placées sur F, nous parlons d'un relation entre X et Y, plutôt qu'une fonction. La relation est «à valeur unique" lorsque la première restriction se applique: (x, y 1) ∈ F (x, y 2) ensemble implique ∈ F y 1 = y 2. Relations qui ne sont pas une valeur unique sont parfois appelés fonctions multiples. Une relation est "totale" lorsqu'une deuxième restriction est titulaire: si x ∈ X alors (x, y) ∈ F pour une y. Ainsi, nous pouvons également dire que
- Une fonction de X à Y est une valeur unique, la relation totale entre X et Y.
La gamme de F, et ƒ, est l'ensemble de toutes les secondes éléments de F; il est souvent désigné par RNG ƒ. Le domaine de F est l'ensemble de tous les premiers éléments de F; il est souvent désigné par dom ƒ. Il ya deux définitions communes pour le domaine de la ƒ certains auteurs définissent comme le domaine de F, tandis que d'autres la définissent comme la source de F.
La cible de ƒ Y est aussi appelé le codomaine de ƒ, notée par la morue ƒ; et la gamme de ƒ est aussi appelé l'image de ƒ, désigné par ƒ im. Le ƒ de notation: X → Y indique que ƒ est une fonction avec le domaine X et Y codomaine.
Certains auteurs omettent la source et la cible des données inutiles. En effet, étant donné que le graphique F, on peut construire une triple approprié en prenant dom F à la source et rng F à la cible; ce qui provoque automatiquement F soit totale. Cependant, la plupart des auteurs en mathématiques avancés préfèrent la plus grande puissance d'expression conférée par le triple, en particulier la distinction entre elle permet gamme et codomaine.
Incidemment, les paires et triplets ordonnés que nous avons utilisées ne sont pas distinctes de jeux; nous pouvons facilement les représenter au sein de la théorie des ensembles. Par exemple, on peut utiliser {{x}, {x, y}} pour le couple (x, y). Ensuite, pour un triplet (x, y, z), on peut utiliser le couple ((x, y), z). Une construction important est le Produit cartésien d'ensembles X et Y, notée X × Y, qui est l'ensemble de toutes les paires possibles commandé (x, y) avec x ∈ X et y ∈ Y. Nous pouvons également construire l'ensemble de toutes les fonctions possibles du jeu X pour mettre Y, que nous noterons soit [X → Y] ou Y X.
Nous avons maintenant une grande flexibilité. En utilisant des paires pour X nous pouvons traiter, dire la soustraction de nombres entiers en fonction, sous: Z × Z → Z. En utilisant paires Y nous pouvons tirer une courbe plane en utilisant une fonction, crv: R → R × R. Dans l'intervalle unité, je, nous pouvons avoir une fonction définie comme l'un des nombres rationnels et à zéro autrement, rat: I → 2. En utilisant les fonctions de X nous pouvons considérer une intégrale définie sur l'intervalle de l'unité pour être une fonction, int: [I → R] → R.
Pourtant, nous ne sommes pas encore satisfaits. Nous pouvons voulons encore plus générale, comme une fonction dont l'intégrale est un fonction de l'étape; Ainsi, nous définissons le soi-disant fonctions généralisées. Nous pourrions moins généralité, comme une fonction nous pouvons toujours utiliser effectivement pour obtenir une réponse définitive; Ainsi, nous définissons fonctions récursives primitives et puis nous limiter à ceux que nous pouvons prouver sont effectivement calculable. Ou nous pouvons vouloir porter définit pas seulement, mais les structures algébriques , complète avec des opérations; Ainsi, nous définissons homomorphismes.
Histoire
L'histoire de la notion de fonction en mathématiques est décrit par da Ponte (1992). En terme mathématique, «fonction» a été inventé par Leibniz en 1694, pour décrire une quantité liée à une courbe , par exemple une courbe de pente à un particulier Point. Les fonctions Leibniz considérée sont aujourd'hui appelé fonctions différentiables . Pour ce type de fonction, on peut parler de limites et dérivés ; les deux sont des mesures de la production ou la variation de la sortie car elle dépend de l'entrée ou de la modification de l'entrée. Ces fonctions sont la base de calcul .
La fonction de mot a été utilisé plus tard par Leonhard Euler au cours de la mi-18ème siècle pour décrire une expression ou une formule impliquant divers arguments, par exemple ƒ (x) = sin (x) + x 3.
Pendant le 19ème siècle, les mathématiciens ont commencé à formaliser toutes les différentes branches des mathématiques. Weierstrass préconisé la construction tartre sur l'arithmétique plutôt que sur la géométrie , ce qui a favorisé la définition d'Euler sur Leibniz (voir arithmétisation de l'analyse).
Au début, l'idée d'une fonction était plutôt limitée. Joseph Fourier, par exemple, affirmé que chaque fonction a eu un série de Fourier, quelque chose qu'aucun mathématicien prétendre aujourd'hui. En élargissant la définition des fonctions, les mathématiciens ont pu étudier des objets mathématiques "étranges", comme fonctions continues qui sont nulle part différentiables. Ces fonctions ont d'abord été pensé pour être seulement curiosités théoriques, et ils ont été appelés collectivement "monstres" pas plus tard que la fin du 20ème siècle. Cependant techniques, de puissants analyse fonctionnelle ont montré que ces fonctions sont en quelque sorte «plus commun» que les fonctions différentiables. Ces fonctions ont depuis été appliquée à la modélisation de phénomènes physiques tels que Mouvement brownien.
Vers la fin du 19ème siècle, les mathématiciens ont commencé à formaliser toutes les mathématiques à l'aide de la théorie des ensembles , et ils ont cherché à définir chaque objet mathématique comme un définir. Dirichlet et Lobachevsky sont traditionnellement crédité de donner indépendamment la définition moderne «formelle» d'une fonction comme une relation dans laquelle chaque premier élément a un second élément unique, mais la demande de Dirichlet à cette formalisation est contestée par Imre Lakatos:
- Il n'y a pas une telle définition dans les œuvres de Dirichlet à tous. Mais il ya suffisamment de preuves qu'il ne avait aucune idée de ce concept. Dans son [1837], par exemple, quand il discute des fonctions continues par morceaux, il dit que dans les points de discontinuité de la fonction a deux valeurs: ...
- (Preuves et Réfutations, 151, Cambridge University Press, 1976.)
Hardy (1908, pp. 26-28) définie comme une fonction d'une relation entre les deux variables x et y tels que "pour certaines valeurs de x correspond à ne importe quel taux valeurs de y." Il requis ni la fonction à définir pour toutes les valeurs de x, ni d'associer à chaque valeur de x pour une seule valeur de y. Cette définition large d'une fonction englobe plus que les relations sont ordinairement considérés comme fonctions mathématiques contemporaines.
La notion d'une fonction comme une règle pour informatique, plutôt que d'un type particulier de relation, a été largement étudié dans la logique mathématique et informatique théorique. Modèles pour ces fonctions calculables comprennent la lambda-calcul, le fonctions μ-récursives et Machines de Turing.
Vocabulaire
Une entrée spécifique dans une fonction est appelée un argument de la fonction. Pour chaque valeur de l'argument x, y l'unique correspondant dans le codomaine est appelé la valeur de fonction en x, ou de la image de x dans ƒ. L'image de x peut se écrire f (x) ou y. (Voir la section sur la notation .)
Le graphique d'une fonction f est l'ensemble de toutes couples (x, ƒ (x)), pour tout x dans le domaine X. Si X et Y sont des sous-ensembles de R, les nombres réels, cette définition coïncide avec le sens familier de "graph" comme une image ou un tracé de la fonction, avec les paires ordonnées étant les coordonnées cartésiennes de points.
Le concept de l'image peut être étendue à partir de l'image d'un point de l'image d'un définir. Si A est tout sous-ensemble du domaine, puis ƒ (A) est le sous-ensemble de la gamme composée de toutes les images d'éléments de A. On dit ƒ (A) est l'image de A sous f.
Notez que la gamme de ƒ est le ƒ de l'image (X) de son domaine, et que la gamme de ƒ est un sous-ensemble de son codomaine.
Le préimage (ou une image inverse, ou plus précisément, image complète inverse) d'un sous-ensemble B de la codomain Y sous une fonction ƒ est le sous-ensemble du domaine défini par X
Ainsi, par exemple, la pré-image de {4, 9} sous la fonction d'élévation au carré est l'ensemble {-3, -2, + 2, + 3}.
En général, la pré-image d'un singleton (un ensemble avec un seul élément) peut contenir ne importe quel nombre d'éléments. Par exemple, si ƒ (x) = 7, puis l'image réciproque de {5} est l'ensemble vide, mais l'image réciproque de {7} est l'ensemble du domaine. Ainsi, la pré-image d'un élément dans le codomaine est un sous-ensemble du domaine. La convention habituelle sur l'image réciproque d'un élément est que ƒ -1 (b) des moyens ƒ -1 ({b}), c.-à-
Trois types importants de la fonction sont les injections (ou un-à-un), qui ont la propriété que si ƒ (a) = f (b), puis un must égale b; la surjections (ou sur les fonctions), qui ont la propriété que, pour chaque y dans le codomaine il existe un x dans le domaine de telle sorte que f (x) = y; et le bijections, qui sont tous les deux un-à-un et sur. Cette nomenclature a été introduit par le Groupe Bourbaki.
Lorsque la première définition de la fonction donnée ci-dessus est utilisé, depuis le codomaine ne est pas défini, le "surjection" doit être accompagnée d'une déclaration sur l'ensemble de la fonction cartes sur. Par exemple, nous pourrions dire cartes ƒ sur l'ensemble des nombres réels.
Restrictions et extensions
Officieusement, un restriction d'une fonction ƒ est le résultat de la coupe de son domaine.
Plus précisément, si ƒ est une fonction d'un X à Y, et S est ne importe quel sous-ensemble de X, la restriction de ƒ pour S est la fonction f | S de S à Y de sorte que ƒ | S (S) = ƒ (s ) pour tous les s en S.
Si g est toute restriction de ƒ, nous disons que ƒ est une extension de g.
Notation
Il est courant d'omettre les parenthèses autour de l'argument quand il ya peu de chance d'ambiguïté, donc: sin x. Dans certains contextes formels, l'utilisation de notation polonaise inverse, x ƒ, élimine la nécessité pour toutes les parenthèses; et, par exemple, la factorielle fonction est toujours écrite n!, même si sa généralisation, le fonction gamma, est écrit Γ (n).
Description formelle d'une fonction implique généralement le nom de la fonction, son domaine, son codomaine, et une règle de correspondance. Ainsi, nous voyons souvent une notation en deux parties, un exemple étant
où la première partie est lu:
- "Ƒ est une fonction de N à R" (on écrit souvent de manière informelle "Laissez ƒ: X → Y» signifie «Let ƒ être une fonction de X à Y"), ou
- "Ƒ est une fonction sur N dans R", ou
- "Ƒ est une fonction de R -Évaluées d'un N à valeurs variable",
et la deuxième partie est lu:
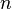 cartes à
cartes à 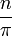
Ici, la fonction nommée "ƒ" a les nombres naturels comme domaine, les nombres réels que codomain et cartes n de se divisé par π. Moins formellement, ce long formulaire peut être abrégé
mais avec une certaine perte d'informations; nous ne sommes plus explicitement donné le domaine et codomaine. Même la forme longue ici abrège le fait que le n sur le côté droit est silencieusement traité comme un nombre réel en utilisant le plongement standard.
Une alternative à la notation du côlon, au moment opportun fonctions sont composées, écrit le nom de la fonction dessus de la flèche. Par exemple, si ƒ est suivie par g, où g produit le nombre complexe e i x, on peut écrire
Une forme plus élaborée de ce est la diagramme commutatif.
Utilisation de ƒ (A) identifiant l'image d'un sous-ensemble A ⊆ X est conforme tant qu'aucun sous-ensemble du nom de domaine est également un élément de nom de domaine. Dans certains domaines (par exemple dans la théorie des ensembles, où ordinaux sont aussi des ensembles de ordinaux), il est commode ou même nécessaire de distinguer les deux concepts; la notation habituelle est ƒ [A] pour l'ensemble {ƒ (x): x ∈ A}; certains auteurs écrivent ƒ` x au lieu de f (x), et ƒ`` ƒ A au lieu de [A].
Composition de Fonction
La composition de la fonction de deux ou plusieurs fonctions utilise la sortie d'une fonction que l'entrée de l'autre. Par exemple, f (x) = sin (x 2) est la composition de la fonction sinus et la fonction d'élévation au carré. Les fonctions ƒ: X → Y et g: Y → Z peuvent être composées en appliquant d'abord ƒ à un argument x pour obtenir y = ƒ (x) et en appliquant ensuite g à y obtenir z = g (y). La fonction composite formé de cette manière à partir de g ƒ général et peut se écrire
La fonction sur la droite agit d'abord et la fonction sur la gauche agit secondes, renversant l'anglais ordre de lecture. Nous nous souvenons de l'ordre par la lecture de la notation comme «g de ƒ". L'ordre est important, parce que rarement pouvons-nous obtenir le même résultat dans les deux sens. Par exemple, supposons que f (x) = x 2 g (x) = x 1. Ensuite g (f (x)) = x 2 + 1, alors que f (g (x)) = (x 1) 2, qui est 2 x 2 x 1, une fonction différente.
la fonction d'identité
La fonction unique sur un ensemble X qui mappe chaque élément se est appelée la fonction d'identité pour X, et généralement désigné par id X. Chaque jeu a sa propre fonction d'identité, donc l'indice ne peut être omise sauf si l'ensemble peut être déduite à partir du contexte. Sous la composition, une fonction d'identité est «neutre»: si ƒ est une fonction de X à Y, puis
Fonction inverse
Si ƒ est une fonction de X à Y alors une fonction inverse pour ƒ, désigné par ƒ -1, est une fonction dans la direction opposée, de Y à X, avec la propriété que d'un aller-retour (une composition ) retourne chaque élément lui-même. Non chaque fonction a un inverse; ceux qui le font sont appelés inversible.
Comme un exemple simple, si ƒ convertit une température en degrés Celsius à des degrés Fahrenheit, la fonction de conversion degrés Fahrenheit en degrés Celsius serait une -1 ƒ approprié.
La notation pour la composition nous rappelle de la multiplication; En fait, parfois on note à l'aide de la juxtaposition, g ƒ, sans cercle intervenir. En vertu de cette analogie, fonctions d'identité sont comme une, et inverses sont comme inverses (d'où la notation).
Spécifiant une fonction
Une fonction peut être définie par ne importe quelle condition mathématique relative à chaque paramètre la valeur de sortie correspondant. Si le domaine est fini, une fonction ƒ peut être définie par tabulation simplement tous les arguments x et leurs valeurs correspondantes de la fonction ƒ (x). Plus généralement, une fonction est définie par une formule , ou (plus généralement) un algorithme - une recette qui raconte comment calculer la valeur de ƒ (x) donné aucun élément x dans le domaine.
Il ya beaucoup d'autres façons de définir les fonctions. Des exemples comprennent récursivité, ou algébrique analytique fermeture, limites , prolongement analytique, infini série, et que les solutions à intégrales et différentielles équations . Le lambda-calcul fournit un puissant et flexible syntaxe pour la définition et la combinaison des fonctions de plusieurs variables.
Calculabilité
Fonctions qui envoient entiers en entiers ou des chaînes finies à finie, cordes, peuvent parfois être définis par un algorithme , qui donne une description précise d'un ensemble d'étapes de calcul de la sortie de la fonction de son entrée. Fonctions définissables par un algorithme sont appelés fonctions calculables. Par exemple, le Algorithme d'Euclide permet un procédé précis pour calculer le plus grand commun diviseur de deux nombres entiers positifs. La plupart des fonctions étudiées dans le cadre de la théorie des nombres sont calculable.
Les résultats fondamentaux de théorie de la calculabilité montrent que il ya des fonctions qui peuvent être définies avec précision, mais ne sont pas calculable. De plus, dans le sens de la cardinal, presque toutes les fonctions des entiers dans les entiers ne sont pas calculable. Le nombre de fonctions calculables à partir des nombres entiers en entiers est dénombrable, parce que le nombre d'algorithmes possibles est. Le nombre de toutes les fonctions des entiers dans les entiers est plus élevé: le même que le cardinal des nombres réels . Ainsi, la plupart des fonctions des entiers dans les entiers ne sont pas calculable. Des exemples spécifiques de fonctions incalculable sont connus, y compris la fonction et fonctions de castor affairé liée à la problème de l'arrêt et d'autres problèmes indécidables.
Fonctions avec plusieurs entrées et sorties
La notion de fonction peut être étendu à un objet qui prend une combinaison des deux (ou plus) valeurs d'argument à un seul résultat. Ce concept intuitive est formalisée par une fonction dont le domaine est le Produit cartésien de deux ou plusieurs ensembles.
Par exemple, considérez la multiplication fonction qui associe deux entiers à leur produit: ƒ (x, y) = x · y. Cette fonction peut être défini officiellement comme ayant un domaine de Z × Z, l'ensemble de toutes les paires d'entiers; codomain Z; et, pour le graphique, l'ensemble de toutes les paires ((x, y), x · y). A noter que le premier composant d'une telle paire est elle-même une paire (des entiers), tandis que le second composant est un entier.
La valeur de la fonction de la paire (x, y) est f ((x, y)). Cependant, il est de coutume de déposer un ensemble de parenthèses et d'envisager ƒ (x, y) une fonction de deux variables (ou avec deux arguments), x et y.
Le concept peut encore être étendue en considérant une fonction qui produit également une sortie qui est exprimée en tant que plusieurs variables. Par exemple, considérons la fonction de miroir (x, y) = (y, x) avec R x R domaine et codomaine R × R ainsi. Le couple (y, x) est une valeur unique dans le codomaine considéré comme un produit cartésien.
Les opérations binaires
Le familier opérations binaires de l'arithmétique , plus et la multiplication , peuvent être considérés comme des fonctions de R × R à R. Ce point de vue est généralisé dans l'algèbre abstraite , où les fonctions n -aire sont utilisés pour modéliser les opérations de structures algébriques arbitraires. Par exemple, un résumé groupe est défini comme un ensemble X et une fonction ƒ de X × X à X qui satisfait certaines propriétés.
Traditionnellement, l'addition et la multiplication sont écrites dans le notation infixée: x + y et x × y + au lieu de (x, y) et x (x, y).
des espaces de fonction
L'ensemble de toutes les fonctions d'un ensemble X à un ensemble Y est notée X → Y, par [X → Y], ou en Y X. Cette dernière notation est justifiée par le fait que | Y X | = | Y | | X | et est un exemple de la convention de la combinatoire énumérative qui fournit des notations pour les jeux en fonction de leurs cardinalités.
Voir l'article sur le nombre de cardinaux pour plus de détails.
On peut interpréter ƒ: X → Y signifie ƒ ∈ [X → Y]; ce est, "ƒ est une fonction de X à Y".
Opérations ponctuelles
Si ƒ: X → R et g: X → R sont des fonctions avec X domaine commun et un codomaine commune anneau R, alors on peut définir la fonction de somme ƒ + g: X → R et la fonction du produit ƒ ⋅ g: X → R comme suit:
pour tout x dans X.
Cela transforme l'ensemble de toutes ces fonctions dans un anneau. Les opérations binaires dans cet anneau ont comme domaine ordonné paires de fonctions, et en tant que fonctions codomaine. Ceci est un exemple de monter en abstraction, pour plusieurs types de fonctions complexes.
En prenant une autre structure algébrique A à la place de R, nous pouvons transformer l'ensemble des fonctions de X à A dans une structure algébrique du même type d'une manière analogue.
Autres propriétés
Il ya beaucoup d'autres classes spéciales de fonctions qui sont importantes pour certaines branches des mathématiques, ou des applications particulières. Voici une liste partielle:
- Bijection. Vous pouvez également visiter fonction injective, Surjection et fonction bijective séparément.
- continu
- différentiables, intégrable
- linéaire, polynôme , rationnel
- algébrique, transcendantal
- trigonométrique
- fractale
- pair ou impair
- convexe, monotone, unimodale
- holomorphe, méromorphe, tout
- valeurs vectorielles
- calculable